基于模糊PID模型预测的电动汽车空调控制研究
2022-05-11方祥建王建平
方祥建,王建平
(1.安徽工程大学 机械工程学院,安徽 芜湖 241000;2.中汽创智科技有限公司 智能底盘事业部,江苏 南京 211100)
当前电动汽车产业发展迅速,但由于电动汽车驱动系统的发热量远远不及内燃机汽车,难于满足冬季座舱内的温度需求。因此,电动汽车大多数采用热敏电阻来提供所需的热量[1]。而夏季气温高,车内由于空间相对较小,热量聚集速度快,需要长时间开启空调来提升车内的舒适度,这也造成了大量的能量消耗。因此,设计一款能耗低、舒适性好的新型空调控制系统对电动汽车尤为重要。
在汽车空调控制器设计方面,杨萍萍等[2]基于模糊比例积分微分(Proportional Integral Derivation,PID)控制算法设计了汽车空调控制器,通过结合模糊控制算法以及PID控制算法建立了汽车空调系统的数学模型,进行了定量的分析计算。管继富等[3]基于随机模型预测控制算法进行了空调系统的数学模型推导,通过算法提升了空调系统能量效率和温度性能,降低了一部分能耗需求。谭文林等[4]结合前馈控制系统及模糊控制策略,建立了汽车空调系统温度控制的模型,通过仿真分析,可以精确地控制汽车空调温度,提升了驾驶舒适性。现有研究中对温度的控制方案较多是应用于温室的温度控制,难以满足汽车行业需求[5-7]。汽车空调系统有非线性强耦合的特点,系统中含有诸多扰动和不确定性。单独使用传统的模糊PID控制虽然能获得较为理想的控制稳定性及精度,但对能量的消耗无法满足电动汽车的需求,采用随机模型预测控制(Model Predictive Control,MPC)虽然可以获得更好的能量利用效率,但在控制的精度和稳定性上有一定的缺陷[8-9]。针对上述问题,本文设计了一个模糊PID的模型预测控制系统,模糊PID有助于提升控制精度,模型预测控制则提供更好的能量利用效率。通过建立汽车空调系统的热负荷数学模型,利用数学模型进行推导。在MATLAB软件上进行数据仿真计算,可以得到系统的能耗及控制性能。
1 汽车热力学系统控制模型
1.1 汽车热干扰负荷模型
汽车热力学结构是一个十分复杂的模型,具有非线性、强耦合、干扰多的特点,很难通过简单的仿真模型建立。汽车热负荷构成图如图1所示。由图1可见,电动汽车的热负荷构成十分丰富,为了方便计算,可以概括为舱内热负荷和舱外热负荷两个部分。舱内热负荷可以分为车内人员热负荷、室内定量热负荷及空调系统热负荷等;舱外热负荷可以分为太阳辐射热负荷、环境热负荷、车体反射热负荷等。

图1 汽车热负荷构成图[3] 图2 汽车热量流动图[3]
汽车热力学系统热量流通模型包括热干扰源及车内空调系统热量流动路径等(见图2)。热干扰源与汽车空调产生的热量共同维持车内热量的稳定。在使用汽车空调制冷时,蒸发器通过吸收热量后转化为热蒸气,再通过冷凝器冷却后送入膨胀阀,膨胀阀的控制管道内的冷却空气进入车内,完成一个制冷循环;制热时,通过热敏电阻产生的热量与舱内热负荷补偿热干扰,形成稳定的热量维持舱内温度。
膨胀阀和压缩机的动力学模型可以采用经验公式建立数学模型[10-11]
(1)
hout,comp=ηis(his-hin,comp)+hin,comp,
(2)
式(2)所表达的是比焓转化关系。hout,comp表示压缩机的出口比焓(j/kg);ηis表示绝热效率;hin,comp表示压缩机入口比焓;his表示制冷剂绝热比焓。
(3)
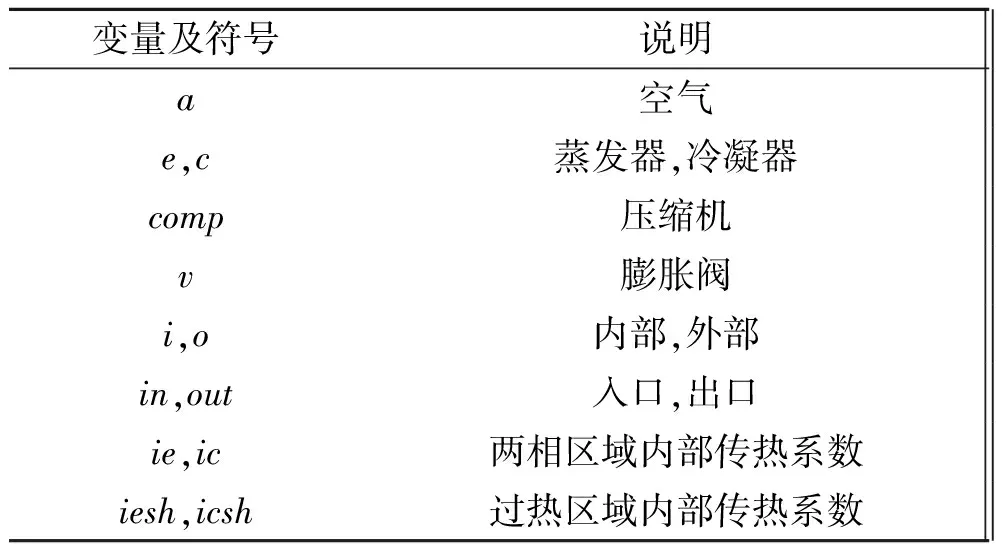
表1 所用公式中字母的含义

变量及符号说明is绝热g,l气体,液体lg制冷剂汽化潜热re,rc饱和制冷剂we,wc管壁w,n车舱内/外表面传热系数p管道t总质量(总辐射强度)
(4)

(5)
式(5)描述的是蒸发器管道中蒸气制冷剂的变化速率。Le表示蒸发器管道长度(m)[3]。
(6)
式(6)描述的是蒸发器管壁的能量平衡公式。Cp表示比热容[J/(kg·K)][3]。
(7)
式(7)描述的是换热器中制冷剂质量[3]。
(8)
式(8)描述的是冷凝器管道蒸气制冷剂的变化速率[3]。
(9)
式(9)描述的是冷凝器管壁的能量平衡公式[3]。
1.2 车内外热负荷模型
车内热负荷是在车内所受到的热负荷,包括车内空气热负荷、车内人员代谢热负荷、空调加热热负荷、蒸发器热负荷、电气设备工作热负荷等,其相应的热负荷公式可以通过计算获得[2]。电气设备热负荷由于发热量较小,对整体温度影响微弱,本文不做考虑。
车内人员代谢热负荷Qm[2]:
Qm=Qd+Qp(n-1)θ,
(10)
式(10)描述的是车内人员代谢热负荷公式。Qd表示驾驶员产生的热量;Qp表示成员产生的热量;n表示车内乘员数量;θ表示人群聚集系数。
车内空气热负荷Qc[2]:
Qc=1 000mΔh=1 000ρcVcΔT,
(11)
式(11)描述的是车内空气的热量值。Δh表示车内空气焓值;ΔT表示室内空气温度值。
车外热负荷包括车身结构反射传导热负荷、太阳直射热负荷、空气热负荷等。其中,车身架构反射传导热负荷Qv[2]:
Qv=KF(Tout-Tin),
(12)
式(12)描述的是车身结构材料等对太阳的反射以及折射过程中的流动热量公式。K表示导热系数,取决于车身材料和结构;F表示车身不传导光结构面积;Tout表示车外空气温度;Tin表示车内空气温度。
太阳辐射热负荷Qs[2]:
(13)
式(13)表示的是太阳辐射热负荷作用在车内的热量。I表示阳光强度系数;Fg表示垂直于光照方向的车窗大小;μ表示太阳辐射的热量通过车窗进入车辆的比例系数;Fs代表非垂直于太阳光照的车窗面积;ρg表示车身吸光系数;αh表示车身与环境热量交换系数。
汽车的扰动热负荷还与时间、地点、空气湿度、驾驶速度、行驶方向等有一定关系,其总扰动热负荷为以上扰动热负荷之和,即
Q=Qs+Qm+Qc+Qv+Qn,
(14)
式中,Qn表示其他热干扰之和,如车辆电气设备发热负荷等,为方便研究取其他未考虑干扰为一个定值,将时间、地点、空气湿度、驾驶速度、行驶方向等看作是不变的[12]。
2 基于模糊PID控制的空调设计
本系统方案所设计的模糊控制器是一个两输入(温度偏差、偏差变化率)、三输出(PID控制器的3个参数Kp、Ki、Kd的变化值)的控制器。在PID控制器的基础上,增加模糊控制器模型所计算的输出,用于提高控制器的适应度,满足不同环境的需求。通过PID来控制空调系统的加热或者制冷量,满足驾驶需求,将车内热量维持在适宜的区间,稳定车内温度。
2.1 模糊化、模糊规则及解模糊
(1)模糊化。模糊化是用于执行清晰量到模糊量的处理任务。设定温度误差e的论域为[-4,4],模糊语言集为[NB,NS,ZE,PS,PB],各元素分别代表[负大,负小,零,正小,正大]。误差变化率ec的论域为[-3,3],模糊语言集为[NB,NM,NS,ZE,PS,PM,PB],各元素分别代表[负大,负中,负小,零,正小,正中,正大],在实际中,若输入的值超出范围,可将其认定为边界值。定义输出值论域为[-5,5],其模糊语言集为[NB,NM,NS,ZE,PS,PM,PB],各元素分别代表[负大,负中,负小,零,正小,正中,正大][8-11]。其对应的隶属度函数如图3~5所示。

图3 温度误差e隶属度函数图

图4 误差变化率ec隶属度函数图

图5 输出隶属度函数图
(2)模糊规则。依据隶属度函数的数学定义,设定输入输出变量的隶属度函数均选用三角形,利用MATLAB中的模糊控制程序进行模糊规则自动生成。当温度误差较大时,误差变化率较小,则输出的值增大,控制空调能够快速调节至目标温度。当温度误差较小,误差变化率较小时,输出的值降低至很弱,代表空调仅需微调保持温度即可。当温度误差在中等幅度,误差变化率在中等幅度,输出值也可以调整至中等幅度。根据经验公式将空调的控制输出量建立了35条模糊规则,生成的模糊规则如表2所示。

表2 模糊控制规则表
(3)解模糊。使用模糊推理能获得模糊量,然而在实际的分析过程中使用的是清晰量,所以应将推理的结果进行反模糊化。反模糊化的常用方式有最大隶属度法、面积重心法(又称重心法)、加权平均法等,本文采用的是最大隶属度法。利用推理输出的模糊集中隶属度最大的元素来作为精确控制量的方式,如果模糊集中多个元素的最大隶属度相一致,则可以随机选取其中一个值作为精确控制量。本文采用MATLAB中的Mamdani模糊推理器进行模糊推理并获取最优值计算[2]。
2.2 模糊PID控制模型
汽车空调系统是一个两输入系统,控制压缩机转速和加热功率,采用试凑法确定最佳的PID控制器初始参数,如表3所示。

表3 压缩机与加热器控制器初始参数[2]
将设计的模糊PID空调控制系统模型在MATLAB系统中仿真,将目标温度设定在25 ℃,初始温度为36 ℃,匀速60 km/h,设定其他干扰为一个常数定值,仿真时间设定为500 s,通过改变车内乘员数量为1人、3人、5人时,得到如图6所示的模糊PID控制器仿真曲线。由图6可以看出,随着车内人数的增加,通过空调降低车舱内温度需要的时间有一定的延长,乘员的热量会对舱内的热量形成干扰。

图6 不同乘员数量下的温度调节仿真曲线
将目标温度设定在25 ℃,车内乘员人数为3人,匀速60 km/h,设定其他干扰为一个常数定值,仿真时间设定为500 s,通过改变车舱内的初始温度为14 ℃、36 ℃、38 ℃时,得到如图7所示的模糊PID控制器仿真曲线。由图7可以看出,在初始温度较高时,温度越高,空调制冷需要的时间越长;在舱内温度较低时,可以实现制热来将舱内温度提升至目标温度。因此,在初始温度不同的情况下,空调的调节时间不同。

图7 不同起始温度下的温度调节仿真曲线
将初始温度设定在36 ℃,车内人员数量为3人,匀速60 km/h,设定其他干扰为一个常数定值,仿真时间设定为500 s,通过改变车内目标温度为22 ℃、26 ℃、28 ℃时,得到如图8所示的模糊PID控制器仿真曲线。由图8可以看出,初始温度一定,目标温度不同时,空调所需要的调节时间不同,距离目标温度误差越大,调节时间越长。
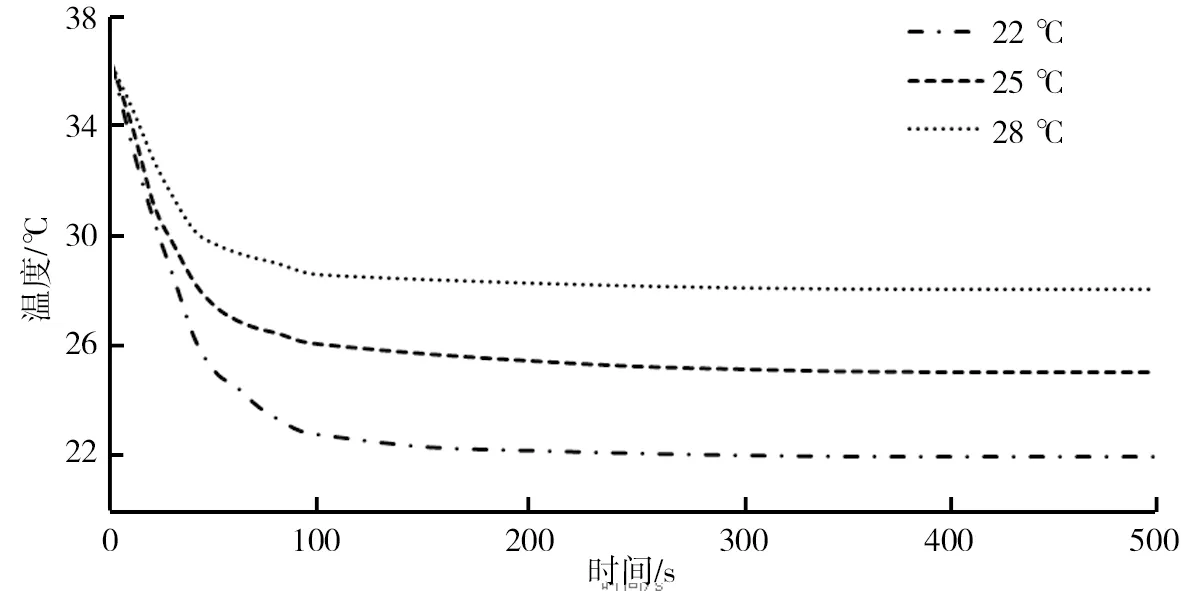
图8 不同目标温度下的温度调节仿真曲线
3 模糊PID模型预测空调系统
模型预测算法因其对多变量复杂系统的控制的优异性能,常用于复杂系统的建模和控制中,其运用过程一般包括3个步骤[2]:系统控制结果预测、合理的滚动优化以及结果的反馈以及校正。模型预测主要原理是结合预测模型、目标函数及约束来计算系统的最优输出,得到当前时刻的最优解后,将当前时刻的最优解输入到被控平台并按照当前的控制量进行控制;然后将当前的控制量结合状态空间约束及目标函数估计出下一时刻的输出量,将估计出来的状态量输入到MPC控制器再进行最优求解,可以得到未来一段时间的控制输出,如此循环往复,即构成了模型预测控制周期,具体如图9所示[13]。

图9 模型预测控制原理图
模糊PID的模型预测空调的系统原理图如图10所示。将温度偏差、偏差变化率输入后,计算出PID控制器的3项初始参数补偿值。补偿值与初始值求和后输入PID控制器中,计算出压缩机及空调加热器的输出转速及输出功率,将输出作用于车内,实现车内热量平衡,满足车内温度需求。MPC控制器则用来计算系统复杂干扰的影响程度,并基于干扰的影响程度来预测控制系统下一步执行的结果。

图10 模糊PID模型预测控制原理图
通常状况下,模型预测的状态空间表达式,如式(15)所示[13]:
(15)
式中,x(k)为k时刻的系统状态值;u(k)为k时刻的控制系统输入;y(k)为系统在k时刻的输出值。在接下来的一段时间内,系统的控制状态输出值可以基于上述模型预测计算出。为了满足系统动态预测未来输出状态的目标,需要给定预测时域内的输入序列,并提供相应的模型预测约束条件,将输出改变为动态优化的结果,在k时刻时,其解如式(16)所示[13]:
Uk={u(k|k),u(k+1|k),…,u(k+Np-1|k)},
(16)
式中,Np为预测时域;Uk为模型预测的k时刻的输出。
根据式(1)~(14)的汽车空调系统热负荷模型,可以将控制方程改写成状态空间表达式:
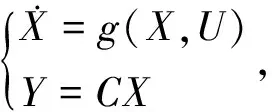
(17)
式(17)表示空调系统的状态空间方程。其中,X为控制系统的状态向量,包括对系统造成影响的温度、湿度、蒸发器压力等;U表示系统的输入状态向量,包括压缩机和加热器的转速及功率。
结合模型预测的计算公式,合并计算为模糊PID模型预测控制系统的状态空间方程如式(18)所示:
(18)
设置其约束条件为空调的最优工作区间,为了更方便MPC控制器运算分析,可以将式(18)的模型定量在一个稳定的工作点,将车舱空间系统线性离散化,进行定量计算仿真,在一个较小的误差内仿真出预测模型的输出跟随性能。将模糊PID计算的数据结合模型预测算法,设计出模糊PID模型预测空调控制系统,再将此系统通过MATLAB进行仿真计算,仿真出模糊PID模型预测算法的性能优劣。
将车内乘员定为3人,起始温度分别设定为36 ℃、14 ℃,匀速60 km/h,目标温度均设定为25 ℃,将数据导入模糊PID模型预测空调控制系统的MATLAB模型中进行数据仿真,仿真时间设定为500 s,得到的仿真结果如图11所示。
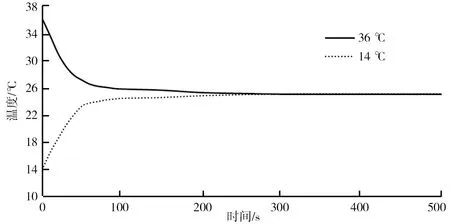
图11 模糊PID模型预测控制空调仿真曲线
4 仿真结果分析
为更好地对比设计方案的优劣,将模糊PID及模型预测算法的空调控制系统进行对比仿真分析,将分析结果与模糊PID模型预测的空调控制系统进行对比。仿真设定车内乘员为3人,起始温度设置为36 ℃,目标温度设置为25 ℃,匀速60 km/h,仿真时间同样设定为500 s,得到的仿真结果如图12所示。
在不同控制方案下,将计算的空调的工作功率进行时间积分可得到不同方案下的空调控制的能耗参数,其结果如图13所示。由图12、13的数据可以看出,在环境温度、车数及乘员人数等干扰因素一定时,模糊PID模型预测控制的空调控制系统的温度控制时间最短,可以更加快速地将温度降低到目标温度,且能够很好地保持目标温度。同时模糊PID模型预测空调控制系统的能耗相对于模糊PID或者模糊模型控制的空调系统更低,可以有效地节省电动汽车能耗。通过表4可以看出,相对于模糊PID算法,模糊PID模型预测算法将温度降低到目标温度5%之内的时间提升了14.38%,相对于模型预测算法,其控制时间提升了20.12%;而以到达目标温度的时间上看,模糊PID模型预测算法相比于模糊PID算法提升了14.48%,相比于模型预测算法提升了16.34%;且其能耗与模糊PID算法相比降低了13.44%,相比于模型预测算法能耗降低了12%。

图12 不同控制方案下的空调控制仿真曲线
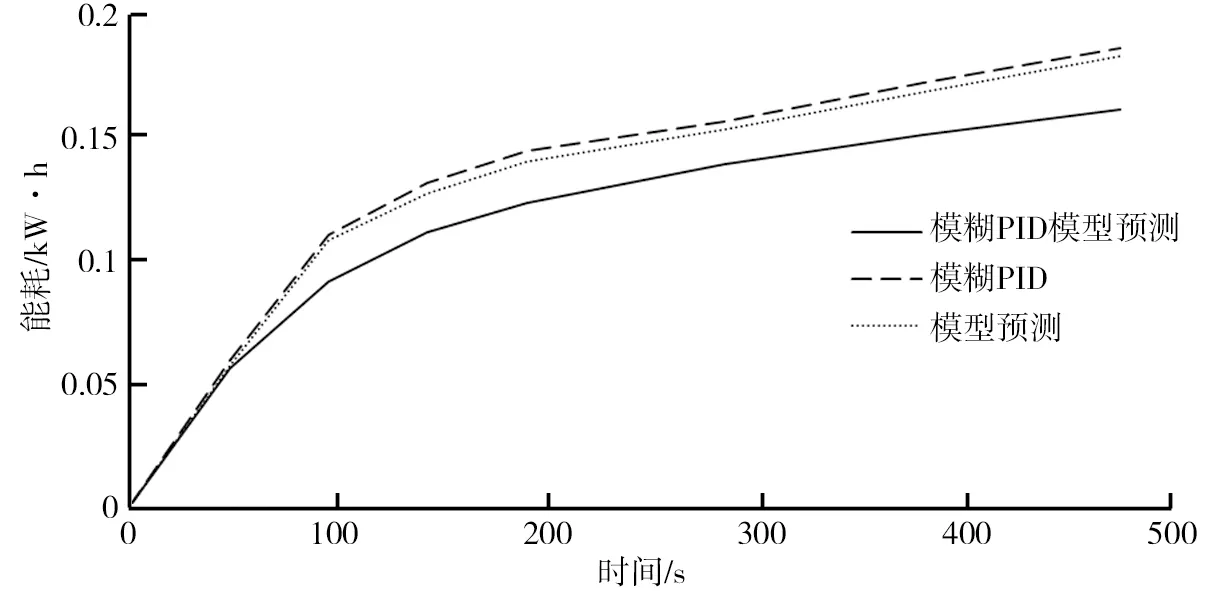
图13 不同控制方案下的空调系统能耗仿真曲线

表4 不同控制方案下的空调系统仿真数据对比
5 结论
本文将模糊PID模型预测算法应用到电动汽车空调控制中,通过MATLAB对设计思路进行数学建模与仿真,通过模糊PID计算出快速达到目标温度的最优功率输出。模型预测用于提高系统的抗干扰能力,使得系统在环境温度有明显改变时仍能快速达到目标的温度范围。通过对不同工况、起始温度及目标温度的数据仿真分析,对比出本方案设计的基于模糊PID模型预测控制的空调控制系统在温度的控制性能及能耗上均有相对优势,控制性能良好,可以减少电动汽车的能量消耗,提升电动汽车的续航里程,为后续的电动汽车空调控制提供了新思路。
