墩底可抬升刚构桥模型振动台试验研究

2022-05-11王建涛杨子奇

地震工程与工程振动 2022年2期

吕杨，赵征，王建涛，杨子奇，陈宇

（1.天津城建大学天津市土木建筑结构防护与加固重点实验室，天津 300384；2.新西兰奥克兰大学土木与环境工程学院，奥克兰 1142；3.中国民航大学交通科学与工程学院，天津 300300）

引言

强震作用下，硬质地基上的浅埋基础桥梁结构有可能发生基础抬升。基础发生抬升的桥梁结构的动力特性和地震响应将发生显著变化。在1960年智利大地震中，Housner等［1］发现基础抬升引起结构摇摆减小了结构在地震中的损坏，其主要原因是基础短暂抬升切断了地震动向上部结构传递，进而起到与基础隔震类似的效果。随后Housner开展了摇摆结构的理论研究，将结构简化成放在刚性平面上的刚体，通过理论求解得到刚体在单个正弦波和方波作用下的最小倾覆加速度。其后，很多学者都开展了摇摆结构相关方面的研究工作，如Aslam等［2］在Housner的研究基础上，开展了刚体摇摆的试验研究。Anooshehpoor等［3］首先发现刚体摇摆碰撞可能发生在激励结束前也可能在激励结束之后。后来Zhang等［4］在Anooshehpoor等的研究基础上进一步发现刚体倾覆时有可能不发生碰撞。Lenci等［5］，Dimitrakopoulos等［6］，Voyagaki等［7］得到了刚体结构摇摆倾覆反应谱的理论解。Lv等［8］进一步考虑正弦波激励下斜坡上刚体摇摆，建立了3种倾覆模式的反应谱。为了得到结构倾覆反应的解析解，前述研究大多数都是将结构简化成刚体，振动激励也主要以正弦波和方波为主。

针对桥梁的基地可抬升结构和可摇摆结构，郑越等［9-10］采用Winkler地基梁模型较早考虑了基础提离和地基土塑性效应对桥墩地震反应的影响，研究表明考虑基础提离和地基土塑性后，双柱式桥墩墩顶位移增大、剪力减小，对保护桥墩减小震害是有利的。夏修身等［11］又提出一种适用于顺桥向和横桥向高墩基底摇摆隔震设计方法，研究表明采用基底摇摆隔震的高墩能靠自重平衡地震作用，隔震效果比墩顶隔震更好、更稳定。Hung等［12］对比研究了可抬升基底和刚性固接基础地震响应的主要差异，研究表明可抬升基础能减小墩底弯矩，但桥面梁的水平位移将增大。杜修力等［13］梳理了摇摆概念在桥梁工程中的发展历史，并总结了目前摇摆桥研究的不足之处和发展前景。郝朝伟等［14］研究了基底摇摆隔震在高墩大跨连续刚构桥中的力学原理，研究了隔震装置的理论、力学模型、参数确定以及在有限元中的实现，结果表明基底摇摆隔震的高墩刚构桥在同一地震作用下桥墩最大转角、弯矩都比未采用隔震时小，隔震效果明显。邱文亮等［15］等利用非线性时程分析方法，分析2种不同桥梁结构在地震激励下的非线性地震反应，验证了T形刚构比连续梁能够承受更强的地震。Qin等［16］开展了小比尺单自由度结构的振动台试验，在墩底设计了一个塑性铰，通过对比分析发现基础断开形成摇摆结构时塑性铰的发展小于刚性固接基底。Chen等［17］也开展了可摇摆桥梁结构在水平和竖向地震同时激振时的动力反应，研究表明当考虑竖向地震动时，摇摆桥梁结构更容易发生抬升和碰撞，此后进一步研究了基础抬升产生的碰撞力作用［18］。从已有的研究可以看出，结构频率和地震动卓越频率对桥梁结构地震响应影响显著；摇摆结构的理论研究主要针对简单加速度激励下的简化模型；基底可抬升桥梁结构的理论和数值分析均表明基础抬升可以减小墩底弯矩起到隔震的作用，但相关的研究结果还缺乏振动台试验分析。

文中设计制作了一座基频为1.8 Hz的连续刚构桥并开展振动台试验，通过墩底基础与振动台不同的连接方式，模拟基底固接和基底抬升2种工况。通过2条天然地震动和1条人工地震动输入进行振动台试验，研究了2种工况模型的动力特性及地震响应，进而分析了基础抬升对桥梁结构地震响应的影响规律。

1 试验概况

1.1 模型结构设计

为了分析墩底可抬升对刚构桥地震响应的影响，采用Q690钢设计并制作了一座两跨钢制刚构桥结构模型，设计试验模型频率为1.80 Hz，其模型尺寸和试验模型如图1所示，其中桥面刚度为1.36×105N/m；桥面质量为1 020 kg；墩底质量为115 kg；桥面与墩底的质量比为0.113；结构基频为1.8 Hz；阻尼率为4.4%。由于振动台台面尺寸限制，设计制作了一个刚性悬臂钢框架支撑桥梁模型（如图2），该钢框架由主框和悬臂框组成，主框与振动台台面刚性连接，悬臂框刚性连接到主框架上，并在悬臂框两端设一个平台近似模拟桥台，平台上部安装一排直径40 mm的万向铰轴承，以此保证在地震动激励下，桥梁能在纵桥向发生自由移动。试验时沿纵桥向施加地震动，悬臂钢框架刚度足够大，可近似认为桥墩墩底及桥台处为一致激励。

图1 试验模型示意图Fig.1 Sketch of the test model（unit：mm）

图2 支撑框架模型Fig.2 Support frame model

通过设置2种桥墩基底与振动台的连接方式，模拟基底固接和基底可抬升试验工况。基底固接工况通过高强螺栓将基底与振动台刚性连接；基底可抬升工况模拟在水平地震作用过程中因基底左右摇摆引起的局部抬升，同时限制基底与振动台台面的水平滑动，其方法是在基座四角处焊接四根圆柱滑杆，滑杆与外部滑轨协同工作，滑轨内部安装轴承允许其竖向滑动，基底水平方向运动因滑杆被滑轨约束而被限制，如图3（a）所示，其墩底抬升机理如图3（b）所示。

图3 模型基底示意图Fig.3 Sketch of the pier bottom of the test model

1.2 测点布置

本试验主要通过加速度计、位移计和应变片来测量桥梁结构的地震响应。在桥梁两端设置激光位移传感器和加速度计测量桥梁的纵桥向位移和加速度；在桥墩上下两端粘贴应变片用于测量桥墩应变；在基底四角布置拉线位移计以及沿基底纵向和竖向布置加速度传感器用于测量基底抬升和碰撞加速度。图4为测点布置图。

图4 测点布置图Fig.4 Layout of measurement points

1.3 地震波选择与加载方案

根据结构的周期以及振动台试验的选波要求，共选择2条天然波，1条人工波进行试验。其中2条天然波为1995年神户地震时在日本气象厅（JMA）和神户岛港（KPI）2个地震台站采集的加速度时程，选用南北分量，其峰值加速度分别为8.25 m/s2和3.41 m/s2，均属于近场地震动。为了防止结构发生破坏，3条地震动的峰值加速度均调幅为1.5 m/s2。3条地震动的加速度时程及傅里叶变换如图5所示。

图5 （续）Fig.5（Continued）

图5 地震动时程曲线及傅里叶变换结果Fig.5 Time histories of earthquake motions and FFT amplitude

将试验加载分为8个工况进行，试验中仅沿桥梁纵桥向输入地震动，各工况编号及具体加载情况如表1所示，试验工况中对模型进行白噪声输入，测定模型动力特性。

表1 试验加载工况表Table 1 The load events

2 地震响应及分析

2.1 桥梁结构动力特性

采用白噪声扫频获得桥面梁水平方向加速度时程响应，通过对加速度响应进行快速傅里叶变换，得到固定基底和可抬升基底桥梁结构基频如图6所示。由图可知，固定基底的结构基频为1.831 Hz，可抬升基底的结构基频为1.648 Hz。墩底脱开降低了桥梁结构刚度，进而结构基频也有所降低。

图6 桥梁加速度的傅里叶变换Fig.6 The FFT of girder acceleration

2.2 基底抬升动力响应

采用可抬升基底时，地震作用下基底将与刚性地面脱开，在重力作用下桥墩将复位并与刚性台面发生碰撞耗散部分能量。以JMA地震动为例，桥墩基底竖向加速度响应如图7（a）所示，对应的基底抬升位移如图7（b）所示。基底最大抬升位移为1.6 mm，发生在2.58 s时刻。当基底在重力作用下复位时与振动台台面接触产生撞击，撞击均发生在基底抬升之后，整体表现出基底抬升与碰撞相一致的现象。为了研究地震动特性对基底抬升和碰撞的影响，对JMA地震动进行短时傅里叶变换（STFT），如图7（c）所示，图中各时刻和频率的傅里叶幅值以彩色条带的颜色表示。由图可以看出，JMA地震动的能量主要集中在3～10 s之间，对应的频率为1～3 Hz，这与图5（a）傅里叶变换结果相吻合。由STFT结果可以看出，地震动的第1个能量峰值点大约在2.5 s时出现，对应的地震动卓越频率约为1.26～2.37 Hz，可抬升基底结构的基频刚好位于该频率范围之内，此时桥梁结构基底发生较明显抬升，最大抬升位移发生在2.58 s。

地震动的第2个能量峰值在5.32 s时刻，此时地震动的卓越频率约为2.845 Hz，由图7（b）可知，此时桥梁结构基底抬升并不明显。地震动的第3个能量峰值在6.26 s时刻，此时地震动的卓越频率约为1.633 Hz，对比图7（b）可知，虽然此时地震动的能量并不是很大，但结构基底抬升很明显。由此可知，当地震动的卓越频率与被激振结构自振频率相近时，激励的频率比加速度幅值对结构的地震响应影响更大。超过前述3个能量峰值后，桥梁墩底在后续较小的地震动幅值作用下发生自由摇摆振动。

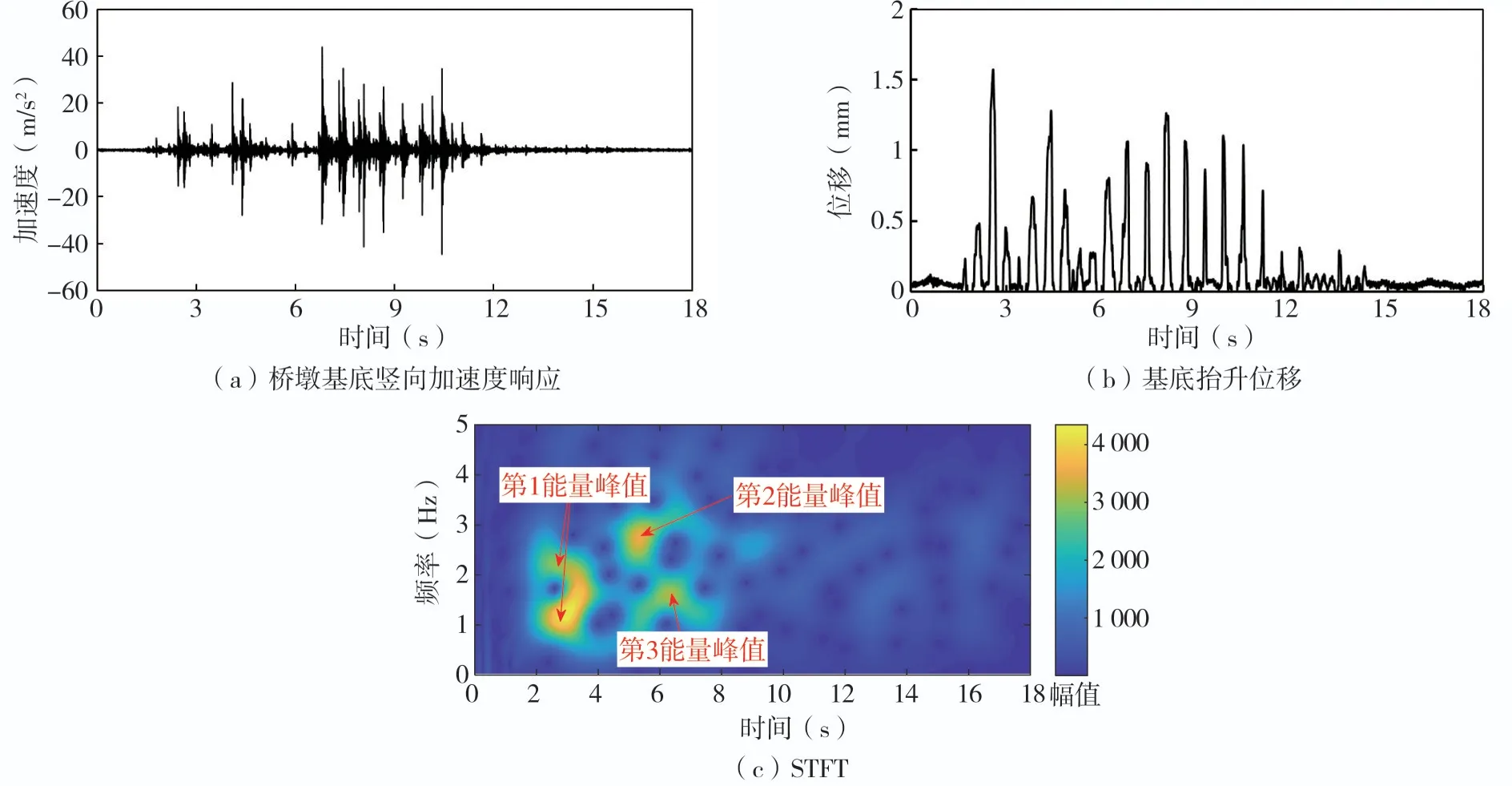
图7 JMA地震动作用下的基底抬升动力响应Fig.7 Footing uplift responses under JMA motion

2.3 桥墩位移及弯矩

模型结构桥墩采用的是Q690钢材，在所有地震工况下桥墩均处于弹性工作状态。因此，可以采用所测得的应变计算得到桥墩墩底贴片处钢材的应力，进而得到结构弯矩。弯矩计算方法如下：

式中：E为Q690钢材的弹性模量；εi（t）和σi（t）分别是第i个应变片在t时刻采集得到的应变和计算得到的应力；W为桥墩抗弯截面系数。

在JMA地震动作用下，不同基础形式的桥面梁沿纵桥向位移和桥墩墩底弯矩如图8所示。从图8可以看出，桥梁结构地震响应可以分为2个阶段。第1阶段为0～7 s左右，此时地震激励加速度幅值较大、能量较高，桥梁结构处于受迫振动（见图7（c））。对比固定基底和可抬升基底桥梁结构的地震响应可以看出，基底抬升使桥面梁的最大水平位移从基底固定时的27.2 mm增大到31.9 mm，增大幅度为17.05%；相反，基底抬升使墩底弯矩从基底固定时的1 790.42 N·m降低到1 684.91 N·m，降低幅度为5.89%。这一结论与文献［8］研究成果相吻合。从7 s以后，桥梁结构地震响应进入第2阶段，此时地震激励加速度幅值和能量均较弱，桥梁结构主要处于自由振动阶段。基底抬升显著增大了桥面梁位移和墩底弯矩，分析其原因主要有：（1）桥墩刚度较小并且由高强钢制作，当基底发生抬升时桥墩本身也会发生较大的弯曲变形，弯曲变形存储的弹性势能很难在后续振动过程中耗散；（2）基底抬升高度较小，最大抬升高度仅1.6 mm，因此基底与振动台台面碰撞释放的能量非常有限，此时固定基底桥梁将优于可抬升基底桥梁。

图8 桥梁地震响应时程曲线Fig.8 Time histoy responses of the bridge under earthquake motions

不同地震动作用下桥梁结构最大位移和弯矩如表2所示。在所考虑的3条地震动中，与基地固定的桥梁结构相比，基地可抬升桥梁结构主梁的位移都有所增加、墩底弯矩均有所减小。在KPI地震动作用下，主梁的最大位移由52.5 mm增加到57.0 mm，增大幅度为8.54%，墩底最大弯矩从2 758.78 N·m降低到2 565.67 N·m，减小幅度为7.0%；在人工波作用下，主梁位移由27.6 mm增加到32.3 mm，增大幅度为16.93%，墩底最大弯矩由1 972.03 N·m减小到1 923.36 N·m，减小幅度为2.47%。对比分析3条地震动可以看出，虽然地震动峰值加速度相等，但KPI地震动作用下桥梁结构水平位移显著大于其他2条地震动，分析其原因主要是KPI地震动的能量主要集中在0.5～2 Hz，桥梁结构基频刚好处于这一频率范围之内。