基于Simulink 的城区高压供电运行系统仿真研究

王如义， 周志峰

（上海工程技术大学 机械与汽车工程学院， 上海 201620）

0 引 言

大规模的电力试验是城区高压供电系统稳定发展的重要前提，而在现实中进行大规模的电力试验依旧存在很大的局限性，一是随着电力系统的规模越来越大，试验的复杂性也随着电力系统的实际要求逐渐增加；二是为了保证电力系统的安全性，在实际生活中进行电力系统的相关试验是不符合现实的。 与此同时，供电网络的基础建设成本会随着供电系统的复杂性的增加而增加，高昂的建设成本和系统的复杂程度限制了电力系统试验的进行。 因此，制作出操作简单且能够为复杂的电力试验提供有效的模拟环境的仿真模拟软件，更好的模拟电力系统试验显得尤为重要。 随着电力系统试验的需求，MATLAB 中的Simulink 插件的应用也更加频繁。 本文完成了电气模拟系统主接线的拟定、短路参数的设置、Simulink 搭建一次系统图、二次系统图等主要工作，利用Simulink 仿真软件搭建了一个虚拟的城区高压供电运行系统，为保证仿真电力系统供电可靠运行，由两个110 KV 三相电源经过降压变压器后为负载提供电能，其各自独立运行又互为备用，并且通过速断保护和过流保护组成二次保护系统，可以在系统出现短路故障时迅速将故障部分切除，避免不必要的人员伤害和经济损失。

1 城区高压供电系统相关参数设计

电力系统中的一些参数不规范是系统短路故障发生的主要原因，对短路电流的相关参数进行计算可以为电力系统仿真模型中元件的选取提供依据，三相短路冲击电流、短路容量和短路电流稳态有效值用来检查电气设备的电动力稳定、热稳定和断路器遮断容量等性能。 除此之外，短路电流的计算将有利于分析电力仿真系统中出现的短路故障问题，同时也方便电力系统中二次保护装置的分配以及装置的调试和校正，电力系统中二次系统参数的计算将为保护装置的动作整定提供有利依据。

1.1 短路电流的计算

以图1 中的输电线路等值电路为例来计算三相短路电流相关参数，三相电源共引出两条输电线路即线路＃1 和线路＃2，线路＃2 备用线路的运行状态对线路＃1 没有影响。 首先，在输电线路中设置3 个短路故障位置点，依次设置在三相电源的出口处、输电线路的末端和负载末端，3 个短路点分别表示为、和。

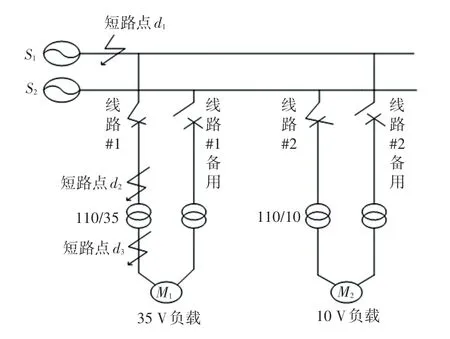
图1 输电线路等值电路Fig.1 Equivalent circuit of transmission line

1.1.1 选择基准值

根据电力系统基准值选取规定，基准容量S ＝100 MVA，基准电压U ＝U ＝105 U（115 KV，38.5 KV）

则点、点和点处的基准电流为式（1）和式（2）：

其中：U为额定电压；点和点的额定电压为110 KV；点的额定电压为35 KV；则、和点的基准电压为115 KV、115 KV 和38.5 KV。

1.1.2 计算各元件电抗

电源的电抗，式（3）：

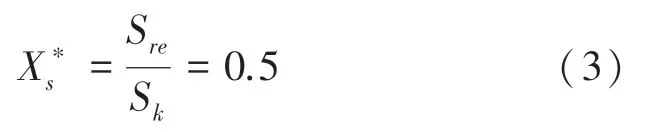
其中：S为基准容量（100 MVA），S为两电源的总基准容量（200 MVA）。

输电线路的阻抗，式（4）和式（5）：

电抗：

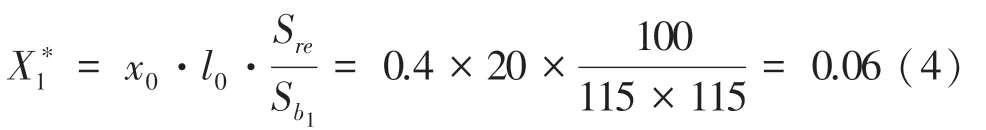
其中，为输电线路长度，为电缆的横截面半径。

电阻：

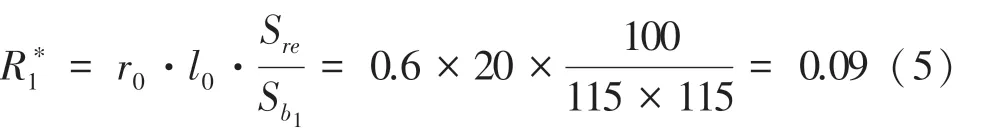
其中，为输电线路长度，为电缆单位长度的电阻。

变压器的电抗，式（6）和式（7）：

其中， ΔU%为变压器的阻抗电压百分比， S为线路＃1 中变压器的容量值。

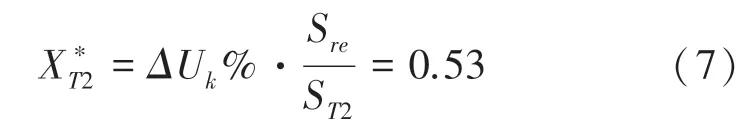
其中： ΔU%为变压器的阻抗电压百分比， S为线路＃2 中变压器的容量值。

1.1.3 等值电路

将输电线路中的所有元件用等值阻抗代替，即可得到对应的等值电路，电源供电等值电路。

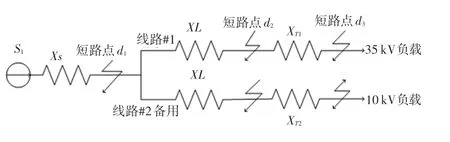
图2 电源S1供电等值电路Fig.2 Power supply S1 power supply equivalent circuit

举例：计算点三相短路电流。

点短路的总电抗，式（8）：

三相短路电流周期分量的标么值，式（9）：

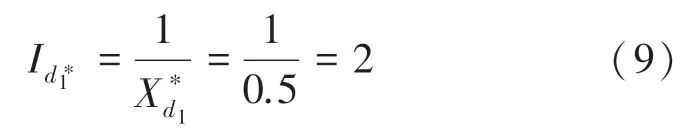
三相短路电流周期分量的实际值，式（10）：

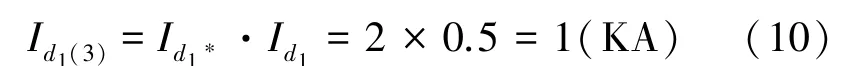
冲击电流，式（11）：

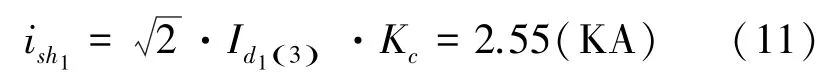
其中，K为冲击系数，取1.8。

冲击电流有效值，式（12）：

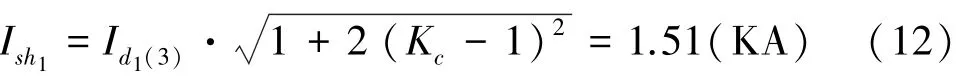
其中：K为冲击系数，取1.8。

三相短路容量，式（13）：

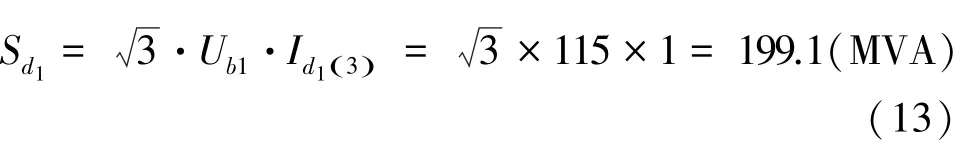
同样的原理，可以求出点和点短路电流。

1.2 二次保护系统相关参数计算

本研究模拟了电流速断保护和过电流保护对电力系统的保护作用，以下为两种保护动作整定值的计算过程。

（1）变压器的额定容量计算，公式（14）和公式（15）：

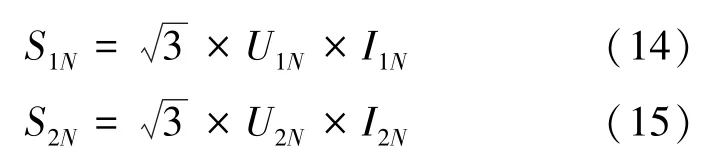
其中：、为线路＃1 中变压器的额定电压和额定电流；、为线路＃2 中变压器的额定电压和额定电流。

（2）变压器低压侧三相短路电流经验计算，公式（16）：

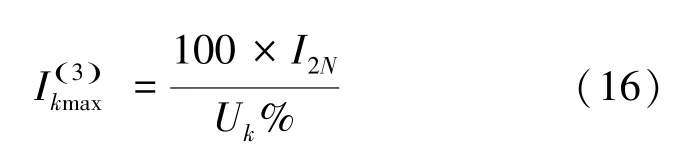
其中，I是最大的三相短路电流， U%是短路电压百分数。

（3）变压器的差动保护动作电流I计算不等式（17）：

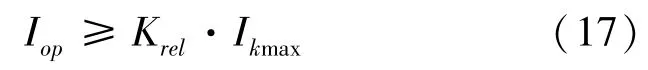
式中：K是可靠系数（为减少非周期分量的影响而引用，取1.3，I保护区外最大负荷电流。

（4）电流速断保护整定的计算：根据避开被保护线路末端最大短路电流的原则整定计算动作电流I，公式（18）：

其中，K ＝13， I是最大短路电流，

（5）过电流保护装置整定值的计算：

（a）依照躲开线路中最大的负荷电流的原则整定计算动作电流I，公式（19）：

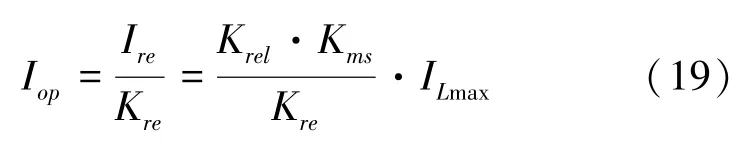
其中，K ＝125；K ＝085；K是自启动系数，与负载性质相关，一般取值1.5 ～3.0；I是线路＃1最大负荷电流，式（20）：

（b）保护装置的灵敏系数S

为了更好的对输电线路进行保护，保护装置需要很高的灵敏度，常用灵敏系数（S） 来表示保护装置的灵敏度，式（21）。

其中：I是线路最小运行方式下的两相短路电流，I是保护装置一次动作电流，公式（22）：

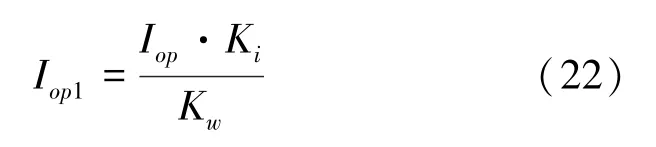
其中：K是电流互感器变比，K是保护装置的接线系数（采用两相继电器接线时取1）。

（c）保护装置的动作时限通常取0.02 ～0.06 s的延迟，并且和下一级保护动作时间配合。

2 基于MATLAB／Simulink 的城区高压供电运行系统建模

2.1 系统参数设置

高压输电线电压和电流的频率均为50 Hz，输电线路的长度设置为20 km；三相电源采用Yg 型连接， 选 择 Internal 和 Specify short － circuit level parameters，相间电压为121 Kv，频率为50 Hz；变压器模块选择标么值pu，额定容量和频率设置为25 MVA、50 Hz，一次侧相间电压设置为121 kV，二次侧相间电压设置为38.5 kV；负载连接方式为Y 型接地，额定相间电压设置为35 kV，频率为50 Hz，有功功率设置为20 kW，容性无功功率为100 var。

2.2 电力系统模型搭建

在Simulink 中建立的一次系统仿真模型，如图3 所示。 当电力系统中的一条输电线路出现故障时，该输电线路中的二次保护装置能够快速检测到参数变化，且对这些变化的参数快速做出反应，将故障部分快速地从电路中切除，同时闭合电力系统中的备用线路的开关。 在Simulink 中搭建的具有保护装置的二次主系统仿真模型，如图4 所示。

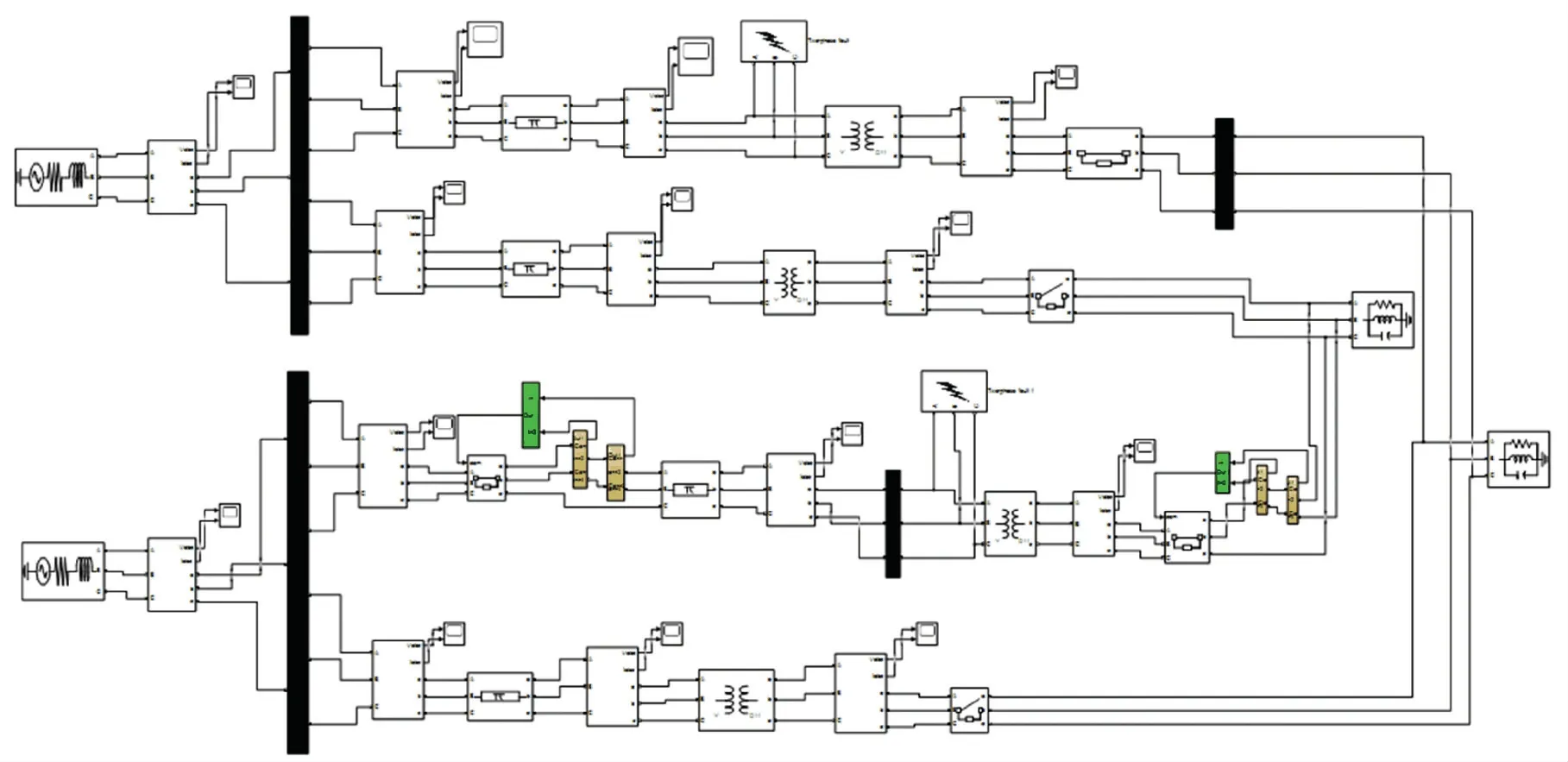
图3 一次系统仿真模型Fig.3 A system simulation model

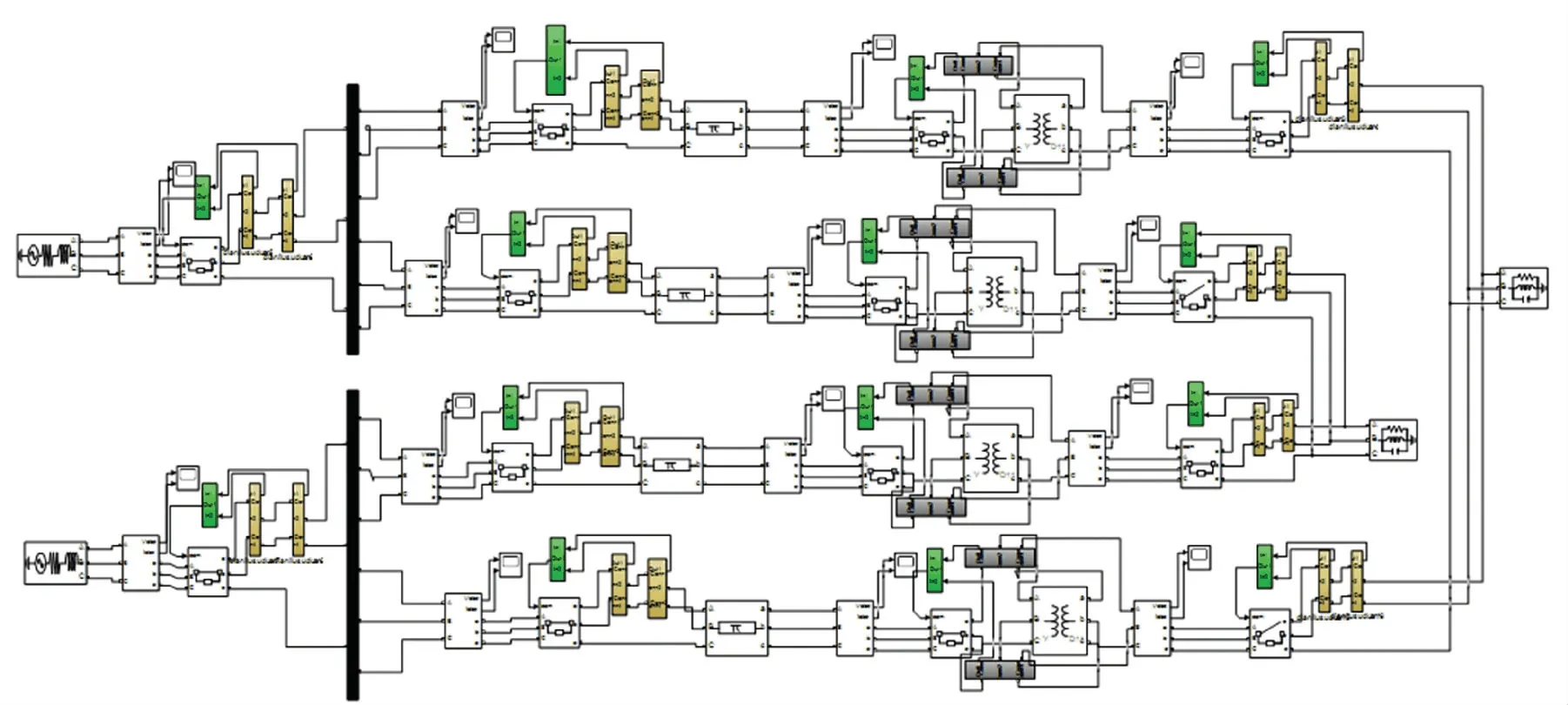
图4 二次主系统仿真模型Fig.4 Secondary master system simulation model

3 Simulink 仿真运行与结果分析

本文给出了在电力系统的电源出口处、输电线路处和负载端的不同状态下的相关仿真结果示例。仿真结果图中，黄线、绿线和红线分别代表A 相、B相和C 相的电流、电压变化曲线。

3.1 电源出口处仿真结果

电源出口处不同状态下的仿真电压、电流波形图如图5 所示。 正常运行时，电压和电流的波形都是正弦波，三相相位差为120°；在0.03 ～0.07 s 内发生三相短路故障时，短路电压变为0，电流瞬时变大，该电源没有受到影响，故电流波形仍然是正弦波；当0.07 s 故障切除后，电压和电流都变为0。

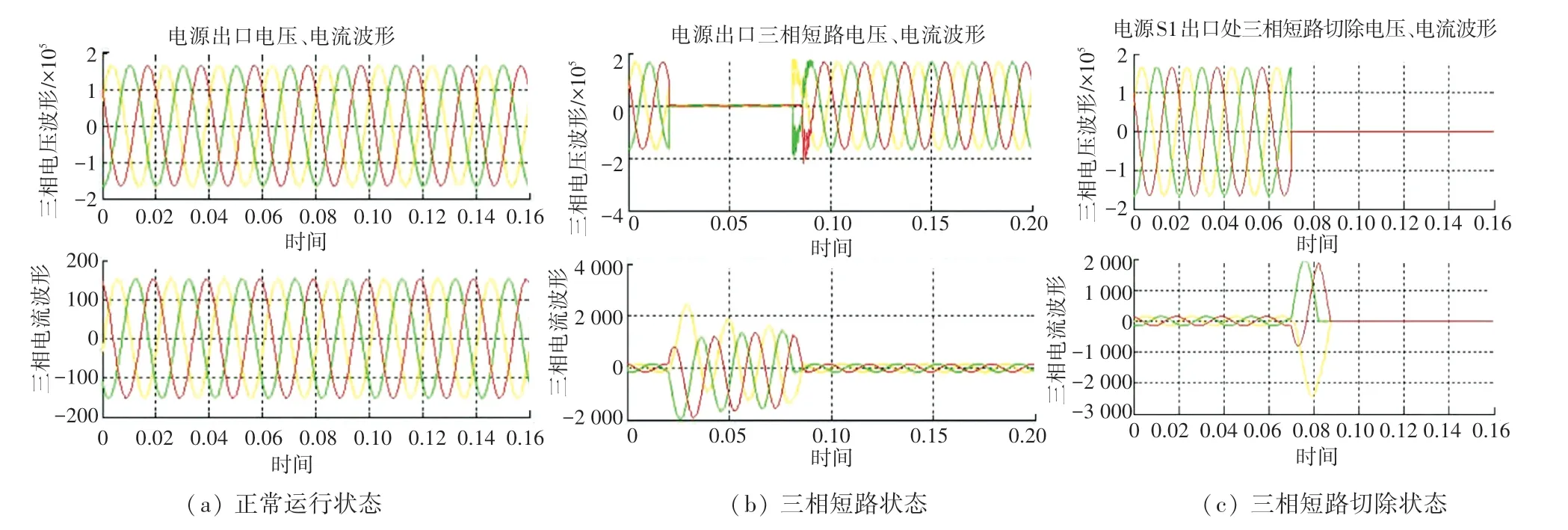
图5 电源出口处仿真曲线图Fig.5 Power outlet simulation curve

3.2 输电线路处仿真结果

输电线路处不同状态下的仿真电压、电流波形图如图6 所示。 正常运行时，电压和电流波形为正弦波，两者对应的幅值是一样的，与理论波形一致；当在0.02～0.07 s 内发生短路故障时，电流变为0；当0.07 s 故障切除后，电压和电流的电位都变为0。

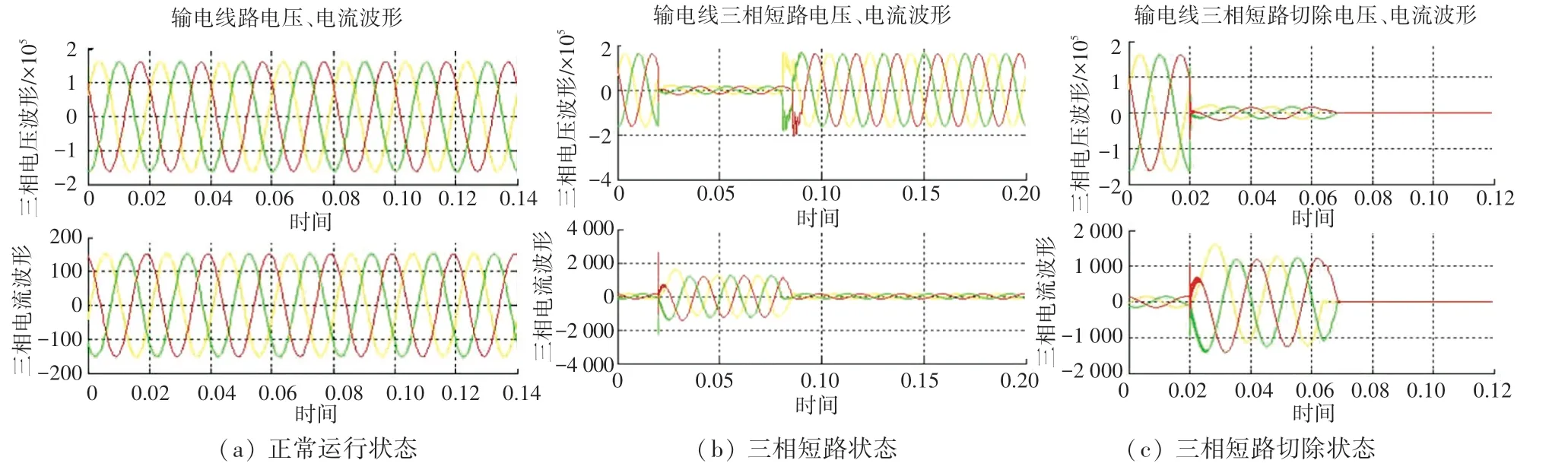
图6 输电线路处仿真曲线图Fig.6 Transmission line simulation curve

3.3 负载端仿真结果

负载端的不同状态下的仿真电压、电流波形图如图7 所示。 在正常运行状态下，A、B、C 三相相位相差120°，波形对应的电压和电流幅值是一样的；在0.06～0.12 s 内发生三相短路故障时，三相短路处电位降低，与地的电位几乎一致，同时电流的幅值增加；在0.06 s短路故障切除后，电压和电流的波形都变为0。

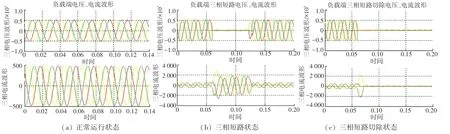
图7 负载端仿真曲线图Fig.7 Load side simulation curve

4 结束语

根据目前城区高压供电系统电力试验的发展现状，本文结合速断保护和过电流保护在电力系统领域的应用前景，基于电力系统的作业特点，对城区高压供电系统进行设计，并在Simulink 仿真环境下结合GUI 功能界面对设计中的城区高压供电系统进行仿真测试。 共设置了十二种运行仿真状态，不仅可以反映电力系统出现短路故障时的三相电流、电压的变化情况，还可以进行二次保护系统对输电线路、电源的过电流保护、负载保护相关方面的仿真实验。 仿真结果说明，城区高压供电系统的安全性和稳定性都能够满足设计要求，仿真结果图和理论计算所得图形基本一致，体现了该电力系统仿真结果的可靠性。