基于记忆网络模型的学习过程评估方法研究

黄轶文

（广东工程职业技术学院 信息工程学院， 广州 510520）

0 引 言

学习过程评估在高等教育中越来越重要。 传统的“小数据”时代，每个教师就是一个数据的小孤岛，依靠自己的直观经验判断，以及考核成绩，来反推学生的学习效果，使得评估效果滞后，无法在教学过程中实时发挥作用。 此外，粗放式的整体评估，无法结合每个学生的特点，为每个受教对象提供有益的参考。 在实际中，各种学习过程评估管理，往往沦为绩效考核的工具，非但没有发挥促进教学的效果，反而成了教师日常工作的负担与桎梏。

2020 年席卷全球的疫情迫使大部分职业院校采用了线上教学模式，因时空距离、设备设施、教学习惯等与传统的在校面对面的方式有很大差异，迫切需要一种符合现实情况的学习过程评估方法，能对教师的“教”与学生的“学”做出回馈，及时调整教学内容和形式，以求在特殊时期不仅保证学生获得正常的学习收益，且学习过程评估结果也能为用人单位提供更有价值的建议和推荐。

本研究分为两大部分：理论研究和应用验证。一方面研究现有学习过程评价模型，创造新型记忆网络模型MMN；另一方面应用理论研究的成果，通过实际数据验证。

1 研究现况

知识追踪模型由Corbett 和Anderson 于1995 年首次提出，并应用于智能教学系统。 随后RS Baker和AT Corbett 等人发现，即使做出相同答案，但学生也具备不同的能力，需要根据学生整体答题情况来进行区分；Pardos 和Heffernan 发现，学生的差异性问题，可以通过增加一个特定的参数解决，为此建立了一个新的BKT 模型；Chen Lin 和Min Chi 则认为，在学习过程中，教学干预是重要的外部因素，影响到教师对学习过程输出的判断。 因此，在标准模型中增加了一个干预点，来仿真学生在学习过程中受到的外界影响；闾汉原、申麟等深入分析了答题过程对评估学生学习过程的影响。 文中认为，对于不同试题所花费的时间是一个重要因子（称之为“态度”），不同的态度反馈出学生对知识点的掌握程度。 “态度”因子的加入，以及通过在线考试数据集的深度学习、模型修正，使得标准BKT 向客观真实性更接近一步。

知识追踪（Knowledge Tracing，KT）以时间为横轴，追踪学生在一系列移动的时间点，对一个或者多个知识点的掌握程度，并可以基于历史数据建模，预测学生未来的学习状态，掌握学生的学习需求。 知识追踪的重要目标是建立学生个性化的学习时间轴，根据学生过去的练习答案，来追踪学生的知识状态。 老师可以根据学生的个人强项和弱项，给出适当的提示和调整练习的顺序；学生可以意识到其学习进展，并可能会投入更多的精力，提高学习效率。

2 知识点追踪模型

目前的智能教学系统（Intelligent Teaching System，ITS），主要使用基于贝叶斯网络的学生知识点追踪模型（Bayesin Knowledge Tracing，BKT）和基于深度神经网络的学生知识点追踪模型（Deep Konwledge Traing，DKT） ，对学生的知识点掌握状况进行追踪判断。

2.1 BKT 模型

BKT 模型最早应用在美国的ITS 体系中。 该模型能对学生知识点的变化序列进行追踪，记录学生知识点掌握情况的变化。 BKT 通过stop＿policy 准则，判断学生是否经过多轮做题，掌握了相应的知识点。 典型的BKT 模型中设置4 个主要参数：

0、、、，用以表示学生掌握这个知识点的概率，一般可以从训练数据里面求平均值获得，也可以使用经验值。 通常情况下，掌握的程度是对半概率，那么当005：表示学生经过练习后，知识点从不会到学会的概率；表示学生没有掌握这项知识点但答对的概率；表示学生实际上掌握了这项知识点，但答错的概率。 模型需要根据学生以往的历史答题系列情况，训练出这4 个对应的参数。

BKT 是根据不同的知识点进行建模，训练数据有多少个知识点，就有多少组对应的参数（、、、）。 标准的BKT 模型无法描述知识点之间的关联关系，当老师布置一项作业时，学生必须应用一个或多个知识点来完成这个任务。 在程序设计中，当学生试图完成“int，int” 的加法运算时，则应采用“整型数值”的概念；当学生试图求解“float，float，float” 的加法运算时，则应采用“浮点型数值”的概念。 学生能够正确回答练习的概率，是基于学生的知识状态，代表了学生掌握基本概念的深度和稳健性。

2.2 DKT 模型

DKT 是一个具有多自由参数的神经网络模型，而BKT 是一个概率模型，拥有有限的自由参数；DKT 对一个领域内所有知识点建模，而BKT 是根据单一知识点构造模型；DKT 是多知识点的交叉输入，而BKT 是按照知识点进行拆分；DKT 是随着时间的推移，所有的知识点都交织在一起的，并按照顺序对每个问题做预测。

现有的方法，如贝叶斯知识跟踪BKT 和深度知识跟踪DKT 以一种特定于知识点的方式或一种概括的隐藏向量来建模学生的知识状态。 在BKT 中，学生的知识点状态被分析成不同的概念状态｛｝ 和BKT 模型，BKT 特定于知识点，而DKT 使用一个总结的隐藏向量来建模知识状态。 本文所用模型可同时维护每个知识点状态，所有知识点状态构成学生的知识状态。 BKT 假设知识点状态为已知和未知的二元潜变量，利用隐马尔可夫模型更新二元概念状态的后验分布。 因此，BKT 不能捕捉不同知识点之间的关系。 此外，为了保持贝叶斯推理的可处理性，BKT 使用离散随机变量和简单的转换模型来描述每个知识点状态的演化。 因此，尽管BKT可以输出学生对一些预定义知识点的掌握程度，但其缺乏提取未定义知识点和建模复杂概念状态转换的能力。

除了从贝叶斯的角度解决问题外，深度学习方法DKT 还利用了一种称为长短期记忆（LSTM）的递归神经网络（RNNs）的变体。 LSTM 假设了底层知识点状态的高维连续表示，与BKT 相比，DKT 的非线性输入到状态与状态到状态转换具有更强的表示能力，不需要人工标记的注释。 然而，DKT 将学生对所有知识点状态归纳为一种隐藏状态，这使得追踪学生对某个知识点的掌握程度和确定学生擅长或不熟悉的知识点变得困难。

3 新型记忆网络模型（MMN）

BKT 和DKT 模型将学习过程评估研究推向了一个新的高度，BKT 具有开发知识点之间关系的能力，DKT 具有跟踪每个知识点状态的能力。 而建立一种新型的模型兼容BKT 和DKT 的能力，是本研究的主要目标。

MMN 通过挖掘知识点之间的关系，使用键静态矩阵存储知识点基本数据，使用值动态矩阵存储和更新相应知识点的掌握程度，能评估学生对知识点的掌握程度，并能评估学生不断变化的知识状态，具有实时性和客观性。

3.1 理论研究

MMN 模型结合了贝叶斯知识跟踪BKT 和深度知识跟踪的优点，开发知识点之间关系的能力和跟踪每个知识点状态的能力。 MMN 能自动学习“练习”和“知识点”之间的相关性，并为每个知识点维护一个状态。 在每个时间戳里，只有相关的知识点状态被更新。 例如， 当一个新的练习q出现时，模型发现q需要应用知识点c和c，然后人们阅读相应的知识点状态s和s，并预测学生是否会正确回答练习。 学生完成练习后，模型将更新这两个知识点状态，所有知识点状态构成该学生整体认知状态。 MMN 模型有一个称为的静态矩阵，其存储知识点，另一个称为的动态矩阵，存储和更新学生对知识点的理解（知识点状态）。 静态和动态矩阵分别类似于字典数据结构（如Python 字典）中的不可变和可变对象作为键和值。

相对于标准的BKT 和DKT，记忆网络模型（MMN）能自动发现知识点之间的联系，并能描述学生不断变化的知识状态。 使得MMN 模型更加符合人类知识追踪的实际情况。

MMN 引入了一个新的参数矩阵，即知识点之间相互影响的参数矩阵：R。 R表示知识点对于知识点的影响。 这意味着当知识点被更新时，关联知识点也会被同时更新。 此外，如果和存在R，则知识点也被更新。 以此类推，凡与知识有直接或者间接联系的知识点都会被更新。 MMN 使用相关权重发现练习的潜在知识点，替代专家手工执行模式，MMN 能描述学生不断发展的知识状态，更好的在数字世界中模拟真实的学习过程。 相关权重表示了知识点内在关系的强度，与标准中的条件影响方法（先计算练习之间的依赖关系，然后定义阈值对练习进行聚类）相比，MMN 可直接将练习分配给知识点，不需要预定义阈值。 新创造的模型能够以智能化的方式发现潜在的知识点，每个练习通常与一个或多个知识点相关联。 在此情况下，可将练习分配给相关权重值最大的知识点。 通过实验验证，MMN 能够智能地学习知识点间的稀疏权重，发现知识点以及之间的联系，并能显示正确的结果。

课程中有个潜在的知识点｛，，…，c｝，存储在键矩阵M（大小为）中，学生对每个知识点的掌握程度，即知识点状态｛，，…，st｝ 存储在值矩阵M（大小为） 中，并随时间而变化。 MMN 使用从输入练习和键矩阵计算的相关权重，通过读写到值矩阵，来跟踪学生的知识。 输入练习q乘以嵌入矩阵（大小为），得到维度为的向量k，通过取k和M（）之间的内积得到权重w（）。

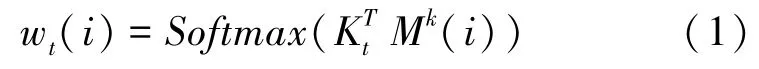
读写过程使用权重向量w、输入练习q。 读取的表达了学生对本练习的掌握程度。

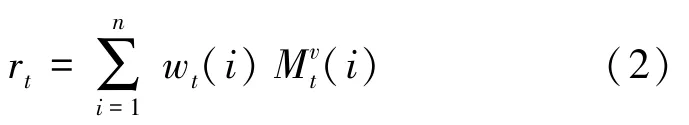
在学生回答问题q后，模型将根据学生回答结果更新值矩阵。 将（q，r） 写入值矩阵，其相关权重w与读取过程中使用的相关权重w相同。 变换矩阵的形状为，e是包含元素的列向量，所有元素都在范围（0，1） 内。

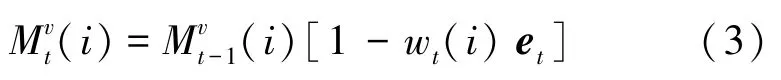
MMN 可以用来描述学生不断变化的知识状态。如果学生掌握了所有知识点的状态，这些状态能表明其长、短之处，使其更有动力，独立地填补学习空白。 MMN 可以通过特定步骤，获得学生不断变化的知识状态，并记录学生在整个学习生命周期里面的起伏状态，输出分析报告，同时能够针对性推荐就业岗位。

3.2 应用验证

本次应用以软件测试知识域为例。 2020 年9月份～2021 年1 月份，以软件测试专业180 名同学为样本，应用MMN 模型进行动态学习过程评估。将软件测试的知识点进行分类，以集合的方式划分为单元测试、集成测试、系统测试和验收测试4 个知识域。 详见表1。

表1 软件测试知识域Tab.1 Software testing knowledge domain

测试期间每月进行一次评估和数据收集，分别是9 月11 日、10 月8 日、11 月2 日、12 月3日和1 月4 日，每次评估由100 道选择题组成，题目涵盖了单元测试、集成测试、系统测试和验收测试4个知识域。 为了便于计算机处理，答案用二进制0、1 表示，0 表示错误，1 表示正确。 同一题目中可以包含单元测试、集成测试、系统测试和验收测试中的一个或多个知识点。 由于传统的考卷方式只能得到笼统的分数，无法分析其中某个知识点的掌握分布情况。 因此，测试评估使用MMN 模型对学生知识水平进行追踪和判断。

共180 名学生参与评估，使用MMN 模型跟踪学生知识域的掌握程度。 数据结果分为三等级：在0.5 以下表示较差、0.5～0.8 为良好、0.8 以上为优秀。 表2 中的数据为全部学生的中位数，另外还为每个学生建立单独数据表，从学生的整体知识掌握情况、群体差异和个体差异等方面来分析和应用评估结果。

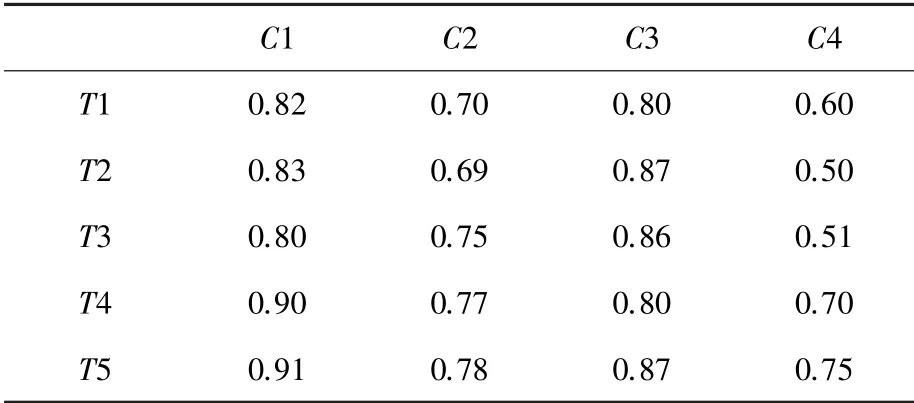
表2 MMN 模型跟踪学生知识域掌握程度中位数Tab.2 The median of students' mastery of knowledge domain tracked by MMN

整体来看，单元测试和系统测试这两个知识域，学生掌握程度良好。 授课教师按照教学计划进行，对课时和课程内容没有做过多调整，成绩预测和实际考核结果呈收敛趋势。 集成测试和验收测试这两个知识域，学生感觉有一定难度，掌握程度一般。 根据跟踪结果，分析具体原因是：

（1）集成测试需要编写测试脚本，需具备一定编程能力；

（2）验收测试要结合实际项目，需根据不用的客户要求，制定测试方案，而学生缺乏项目实操经验，难以理解和灵活应对不同的项目要求。 为此，根据跟踪分析结果，及时采取有关措施：

①调整授课计划，着重培养学生初步编程能力，能够编写基本的测试脚本；

②与合作企业联合，带领学生到项目验收现场，听取客户意见并协助部分工作，对项目验收流程有初步的认知。 经过调整，集成测试和验收测试这两个知识域的掌握程度，呈逐步上升趋势。

与此同时，每个学生根据自己的学习跟踪数据表，认识到个体知识点的掌握程度差异，根据自身条件有针对性地调整学习计划。 学生的个体学习跟踪数据表进入信息化系统，用大数据方法为每个学生进行数据画像，突显学生特点。 在学生求职和企业招聘过程中，数据画像也为企业全面深入了解学生的情况提供了更多的参考。

4 结束语

本研究的价值在于，新型记忆网络模型MMN融合BKT 和DKT 的优点，更加符合人类知识追踪的特点，同时利用模型理论研究的成果，从理论研究到实际应用推进一步。 实践证明在教师侧、学生侧和社会侧，本研究都获得了良好的社会效益。

教师侧：通过学生的个性化、知识、行为、经历建模，学生大数据画像、学生阶段性考核成绩、学生答题时长、知识点分解、关联知识点权重等方式，以直观的图标呈现和分析报告等形式，为教与学的数据挖掘和利用提供了指导。 教师根据学习过程评估的反馈，动态调整教学计划，调整课时计划安排。 可以根据学生个性画像，对薄弱生、薄弱环节、薄弱知识点进行重点研究和加强。

学生侧：在学习过程评估中，通过信息化系统的辅助，建立学习过程全生命周期数据集，把现实中的学生模拟进数字世界，从性格、能力、态度、行为等多维度对学生进行画像。 在学习过程中，同步为学生反馈评价系统的结果，提示学生学习过程中的薄弱环节，调整学习的精力分配。 根据以往学生的学习过程评估，预测学生的学习成绩，增强学习的信心和动力，固化优良学习行为习惯，纠正不良学习行为。

社会侧：按照传统的教学模式，通过试卷得分并不能全面、真实地反映学生特质，也无法向用人单位描绘学生的不同差异。 利用学习过程评估结果分析后，可以较全面的发现学生在不同方面的能力和潜力，从而为用人单位提供更有价值的建议和推荐。