重叠社区检测及其果蝇视觉进化神经网络

罗 兰， 张著洪

（贵州大学 大数据与信息工程学院， 贵阳 550025）

0 引 言

随着科技的快速发展，诸如社交网络、移动通信、博客、微信等已成为社会进步不可或缺的部分。如何从庞大网络中有效发现节点间的关系模式和社区结构，使得网络健康运行，已成为公安、网监等部门关注的现实问题，也是社区检测或社区发现研究所关注的重要科学问题。 社区检测是一种将复杂网络分割为若干社区网络的聚类方法，即将具有相同特性的网络节点归并入同一社区，各社区之间连接稀疏，其中包含非重叠和重叠两种类型社区检测。 前者的每个节点仅属于一个社区，而后者的部分节点可属于多个社区。 由于现实网络中同一节点通常具有多重属性，各节点间的连接也具有多样性，因此重叠是大多数真实网络的重要特征。 由于节点对于不同社区的隶属程度存在较大差异，导致重叠节点与社区之间的隶属关系具有模糊性， 加之真实网络中并没有严格的社区划分界限，使得研究社区网络结构的划分变得较为困难。 2002 年，Newman等针对非重叠社区检测问题，首次提出社区检 测Girvan － Newman （GN） 算 法； 2005 年，Pallaet等针对重叠社区检测，提出派系过滤算法（Cluster Percolation method，CPM）；2011 年Gregory等首次提出模糊重叠划分的概念等等。 此后，一些学者就重叠社区检测展开一系列研究，获得的算法可概括为两种类型，即模糊聚类法及基于进化计算的模糊聚类法。 前者通过构建距离公式来度量节点属于某社区的程度，最后依据相似度进行模糊C 均值聚类，得到重叠社区结构的划分。 但该方法需通过人为设定阈值来确定重叠社区。 后者针对原始模糊聚类FCM （Fuzzy c－means），因初始聚类中心随机确定而导致算法易陷入局部搜索的缺陷，可将进化算法与模糊聚类相结合，设计改进型优化算法。 如，孙延维等提出基于粒子群优化的模糊聚类社区检测方法，利用粒子群优化确定最优聚类中心，再利用FCM 进行社区划分。 Wang等提出一种基于粒子群优化的重叠社区检测方法，将FCM 嵌入粒子群优化算法的粒子选择中，通过最小化模糊J指数来优化聚类中心，但聚类数需人为指定。

综上，重叠社区检测因网络节点连接的多样性，加之常规模糊聚类法应用于社区划分时，分类阈值不具自适应性，导致算法的自适应能力弱、社区检测的精度低。 为此，本文以节点分割的模糊阈值为变量，以社区划分的模块度函数为性能指标，建立重叠社区检测优化模型，进而将果蝇视觉信息处理机制与灰狼优化中位置更新策略结合，提出了求解重叠社区检测问题的果蝇视觉进化神经网络（Fly Visual Evolutionary Neural Network， FVENN）。

1 重叠社区检测模型

1.1 模糊隶属度

将社区网络视为一个无向图，即（，）。 其中，是的顶点（节点） 构成的集合，即｛，，…，v｝；是的所有边构成的集合，即｛（v，v） ｜v∈， v∈，≠｝，。的邻接矩阵是对称的阶布尔矩阵，即（A），A ＝A，且A∈｛0，1｝。 节点的度数为d，1 ≤≤。社区网络中，任意节点可以隶属于多个社区，利用［0，1］连续区间内分布的模糊隶属度，量化重叠节点对不同社区的隶属程度，同一节点对所有社区的隶属度总和为1。 当某节点与某社区的隶属度为0，则该节点完全不隶属此社区；当隶属度为1 时，则该节点完全隶属此社区；当隶属度取值介于01 之间时，隶属度值越大，则该节点属于该社区的隶属程度越高；反之，则越低。 在给定图的划分下，用表示中所有社区的非中心节点构成的集合，即｛，，…｝，中所有中心节点构成的集合表示为｛，，…｝。 另外，距离度量是无向图及社区检测中衡量节点之间连接强度的重要指标，在此利用扩散核相似性度量、图的连接矩阵和节点度数，设计节点间距离计算模型。 具体而言，引入如下关于节点NC与CN之间扩散核相似性度量：

其中，为常数；为拉普拉斯矩阵，即，（L）；是由图中节点的度数构成的阶对角矩阵，其主对角线上位置（，）处的值是节点的度数，非对角线位置处的元素为0。 由于节点间的扩散核相似性与距离具有负相关关系，因此非中心节点NC到中心节点CN之间的距离（NC， CN） 由式（2） 确定：

于是，NC节点属于以中心节点CN为社区C的模糊隶属度由式（3） 计算：

其中，是模糊加权指数，通常取值为2。 若越大，则算法的聚类效果较差，反之则算法退化为硬C 均值聚类（HCM） 算法。 U表示节点NC属于类别CN的程度，U较大，则节点NC属于类别CN的程度高。 由非中心点与社区模糊集确定的隶属度值U构成的隶属度矩阵表示为（U）。 依据此隶属度矩阵和非中心节点NC的分割阈值′进行社区划分，划分规则如下：

其中，r为待定的分割阈值参数。

由以上规则可知，若r越小，则节点NC属于多个社区的几率越大；反之，则仅属于一个社区。

以开源ENZYMES＿g163 网络图为例，取编号为6、8、10 的节点为中心节点，如图1 所示。 依据式（3）获得各非中心节点与社区模糊集的隶属度矩阵，进而在给定非中心节点的待定参数值r下，由式（4）获得非中心节点的分割值；随后，依据以上规则确定非中心节点所属社区。 由该图获知，由于图是一个连通图，加之非中心节点的分割阈值是通过随机方式生成，导致社区分割出现重叠现象。 由此可见，分割阈值在社区检测中起到至关重要的作用。

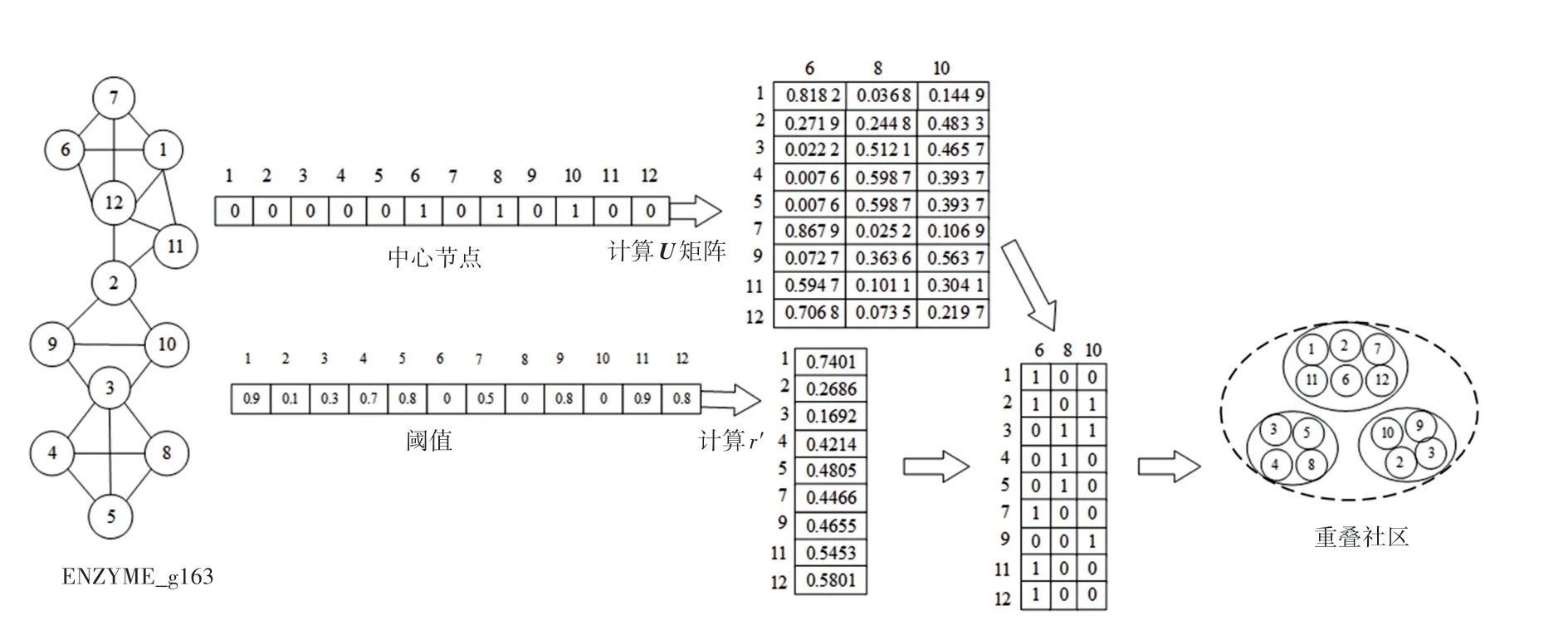
图1 以ENZYMES＿g163 网络的社区检测事例Fig.1 Example of the community detection of the ENZYMES＿g163 network

1.2 重叠社区检测优化模型

Newman等提出一种仅适用于非重叠社区检测的模块度函数，其表示为社区网络图的实际边数与节点随机连接下的期望边数之差。 随后，Shen等针对重叠社区检测问题，将Newman 的模块度函数扩展为如下函数：

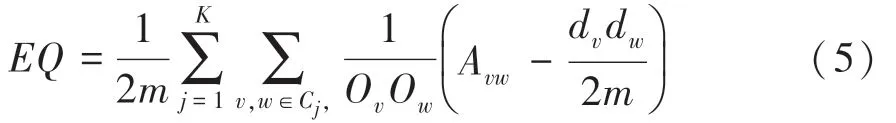
其中，是社区网络无向图的边数；为社区网络划分的社区数；O是节点所属的社区数；d是节点的度数。

式（5） 表明，若值越大，则重叠社区检测的质量越好，即属于多个社区的节点数较少；反之，若值较小，则社区网络中出现多个节点属于多个社区，导致不同社区重叠现象严重。 可是，一旦O和O均大于1 时，OO偏大，进而节点和对值的贡献小，因此在社区重叠现象严重情形下，会导致社区检测效果较差。 为此，借助函数，获得如下改进型模块度（Improved EQ， IEQ）函数：

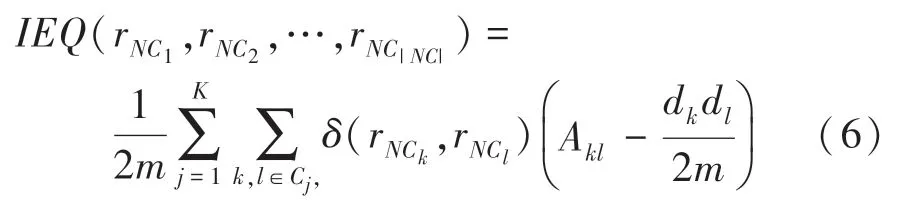
其中，（r，r） 是节点、均属于中心节点为CN的社区C的权值，其由式（7） 确定：

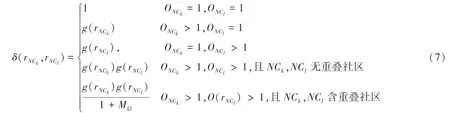
其中，M为节点，属于相同社区的社区数，O是在模糊分割阈值r下非中心节点NC所属的社区数。

式（7） 表明，若节点NC或NC所属社区越多，则（r，r） 越小；特别是，当此节点属于相同社区，则（r，r）更小。 与式（5）相比，式（6）更能刻画含重叠社区的社区划分效果。 于是，为了将图分割为多个社区，使得每个社区内节点之间的连接强度大，不同社区之间包含公共节点的数目尽可能小。 在此，可将重叠社区检测问题（P）用如下模型加以描述：

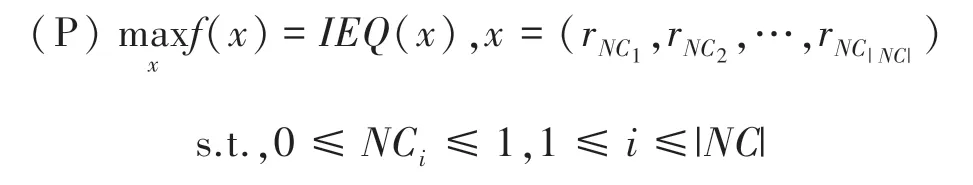
2 果蝇视觉进化神经网络

给定大小为M×N 的状态矩阵(x) ，每个状态是问题（P）的候选解，状态x对应的目标函数值（x） 被视为灰度值，如此状态的灰度值构成大小为的灰度图（）。 第时刻的状态矩阵表示为状态矩阵() ，相应的灰度图表示为（）。 FVENN 作为一种求解优化问题的循环神经网络，以果蝇视觉前馈神经网络在时刻的输出（） 作为全局学习率，经由下式更新状态矩阵中的状态：

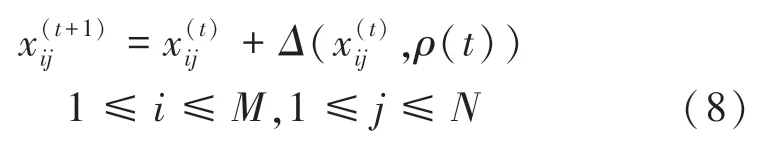
其中，（，） 是经由状态更新策略产生的状态转移增量。

2.1 改进型果蝇视觉神经网络

果蝇视觉系统具有独特的视觉信息处理机制，其主 要 由 光 感 受 器（ Photoreceptor）、 视 网 膜（Retina）、薄膜（Lamina）、髓质（Medulla）和小叶（Lobula）5 层构成，各层的信息处理机制存在显著的差异性。 基于果蝇视觉系统的信息处理机制，文献［13］针对视觉场景下的碰撞检测与预警问题，获得一种人工果蝇视觉神经网络（Artificial Fly Visual Neural Network， AFVNN），其由4 个神经层构成。在此，对该神经网络作适当改进后，得到改进型果蝇视觉神经网络（Improved Fly Visual Neural Network，IFVNN）。 二者的主要区别在于：

（1）AFVNN 的各层大小依次递减，其Lamina 层不仅涉及节点的投影和侧抑制操作，也涉及节点的去极化处理。 同时Lobula 层在汇集Medulla 层中各节点处的运动方向量基础上，基于分流抑制模型产生模型的输出。

（2）IFVNN 的每个神经层均由个节点构成，Lamina 层仅涉及节点的投影和侧抑制操作。IFVNN 的完整设计描述如下，改进型果蝇视觉神经网络结构如图2 所示。

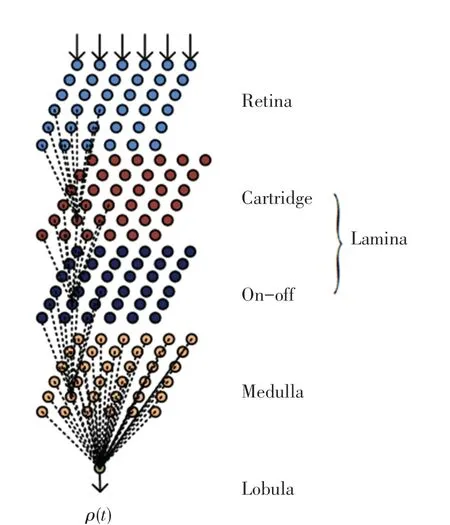
图2 改进型果蝇视觉神经网络Fig.2 Improved fly visual neural network

（1）Retina： 在第时刻， 节点（，） 接收灰度图（） 中像素点（，） 处的光亮强度（即灰度值），并经由式（9） 输出光亮强度的变化量。

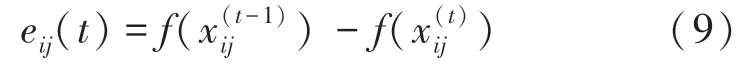
（2）Lamina：由cartridge、on－off 两个子层构成，每个子层的节点数均为。 cartridge 层在Retina 完成扩边处理后，节点（，） 首先接收Lamina 层中对应节点的3×3 邻域节点的膜电位，并经由如下高斯卷积获得输出的膜电位，即

其中，是下列权重矩阵的元数之和，即

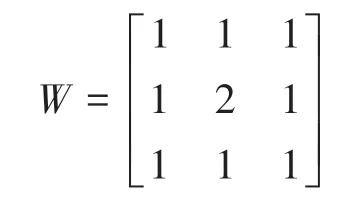
w是位置（，） 处的元素；cartridge 层作扩边处理后，on－off 层中节点（，） 首先接收cartridge 层中对应节点的3×3 邻域内节点的膜电位，进而经由以下侧抑制策略，产生其输出膜电位：

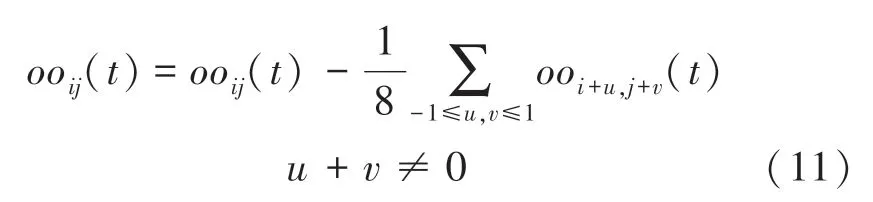
（3）Medulla：此层由节点子层和节点子层构成，且各层的节点规模均为。节点（，）首先接收Lamina 层的节点层中节点（，）的33 邻域节点的输出，然后基于对称EMD 运动方向检测器，获得节点（，） 的输出膜电压，进而经由AFVNN 的设计，获得节点（，）在水平、竖直方向的方向量 （，） 和 （，）。

（4）Lobula：此层首先接收Medulla 层中所有节点在水平、竖直方向的方向量，并经由下式输出其膜电位：

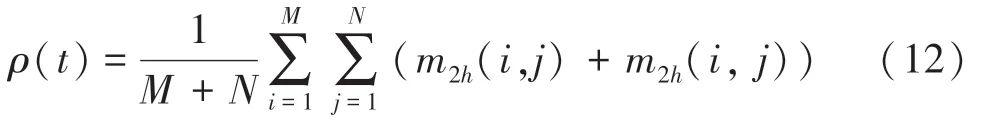
2.2 状态更新

基本灰狼优化算法（Grey Wolf Optimization Algorithm，GWO），是由Mirjalili等受灰狼捕食行为特性的启发，而提出的启发式随机搜索算法。 该算法将优化问题的候选解视为一匹狼，通过狼群捕食猎物过程中不断进行信息交互的行为特性，更新匹狼的位置。 在此，将式（12）的输出作为全局学习率，并利用改进型基本灰狼优化中灰狼的位置更新策略，建立FVENN 的状态矩阵中各状态的更新策略，具体如下：

将中每个状态视为灰狼，依据自身历史最好位置x、 全局最优状态x以及以上IFVNN 输出的学习率（） 更新为，即

其中，是0～1 之间均匀分布的随机数，（）是当前代的自适应扩张系数，即

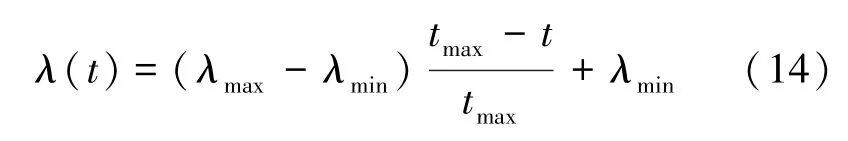
为最大迭代次数；和为预设的自适应扩张系数的边界值；是x与x的线性加权，即

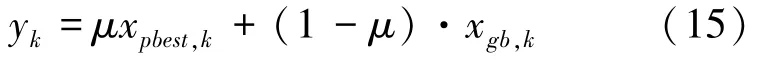
其中，是［0，1］上服从均匀分布的随机数，x是中适应度最大的3 个状态（，和） 产生的平均状态，即

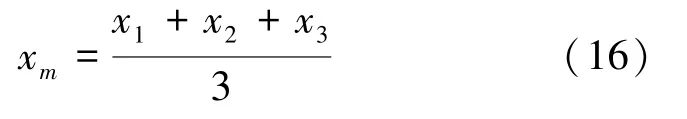
从智能优化角度，在式（13）中，学习率（） 起到全局调节灰狼位置转移幅度的作用；（）引导灰狼逐渐向食物靠近；式（15）使灰狼的位置逐渐介于自身最好位置和食物之间；式（16）使灰狼群中前3匹狼始终处于引领作用，引导其它灰狼进行位置更新，且通过灰狼位置信息交互，确保种群位置的多样性。

2.3 FVENN 算法描述

FVENN 由IFVNN 及状态更新模块构成， 以状态矩阵对应的灰度图作为输入， 产生当前状态矩阵中所有状态转移的全局学习率。 在此学习率引导下，借助以上状态更新策略，使状态矩阵中的状态不断被更新。 FVENN 的算法描述如下：

参数设置： 灰度图大小为，图（，），最大迭代次数为，自适应扩张系数的边界值为和；

确定中心节点集

（1）初始化中心节点集←φ；

（2）将节点集中节点，按其度数降序排列，首个节点放入中；

（3）从中删除及其邻接的节点；

（4）返回步（2），直到为空；

置←1，随机初始化×个候选解（即×个模糊阈值向量） 构成的初始状态矩阵，将全局最好状态记作x；

在［1，］内取随机整数，从集合中随机选择个节点作为中心节点，根据式（3） 计算隶属度矩阵，依据式（6） 计算中各状态的灰度值（）；

根据式（9）～式（12）计算IFVNN 输出的学习率（）；

中所有状态依据式（13）执行状态更新，获得状态矩阵；

计算对应的灰度图（），并借助中所有状态，更新x及各自的x；

依据式（4）及规则I，计算对应的灰度图（）；

置←1，若，则转步骤4；否则，依据式（4）、规则及x， 输出图G 的划分及（x）。

经由以上FVENN 的描述获知， 在状态矩阵从转移过程中，（） 控制状态的变化幅度，引导状态向最优状态转移，提升获得最优社区划分的能力。 同时利用对数函数，对状态分量进行随机扰动，以及引入自适应扩张系数（），增强算法的局部勘测能力。

FVENN 的计算复杂度由IFVNN、状态更新模块以及模块度函数决定。 在IFVNN 中，Retina 层含次加减法； Lamina 层含38次运算；Medulla层含34次四则运算；Lobula 层共需4次加减运算；模块度函数需运算次（为网络节点数）。另外，状态更新模块共需5次乘除、4次加减、次逻辑运算和m（m为优化问题中模块度函数的计算次数） 次目标函数值运算。 因此，FVENN 在一个周期内的运算次数为（（m ＋10）77）。 由此可知，FVENN 的计算复杂度由、、、m确定。

3 数值实验

数值实验环境配置在 Windows10 （CPU／3.7 GHz， RAM／4.0 GB）／Visual Studio 2013 下展开。为测试FVENN 求解重叠社区检测问题的性能，选取两种经典重叠社区检测算法SLPA、NMF以及基于智能优化的重叠社区检测算法（灰狼优化算法GWO及遗传算法GA）参与比较。 测试事例包括真实世界网络和人工合成网络社区检测。 各算法均求解每种事例20 次，最大迭代数为100。 经由参数调试，FVENN 的参数设置为10，08，06；参与比较的方法参数设置与其文献中的参数设置相同。 各算法获得的最大模块度以及信息指标值被用于比较分析。 具体而言，给定网络，某给定算法A 得到的社区划分为，是网络的实际划分。 于是，（）定义为：

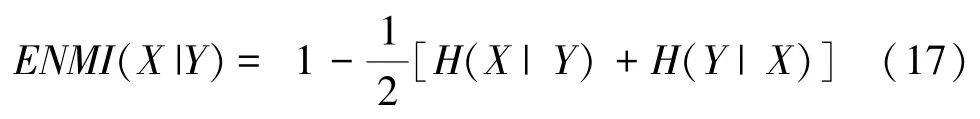
其中，

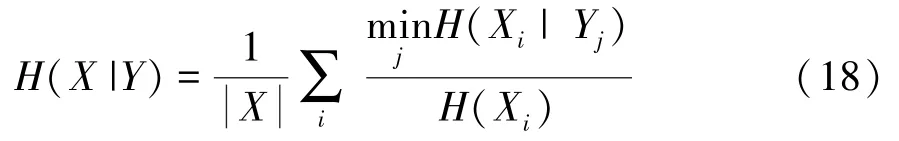
式中，X表示社区划分方式下得到的第个社区；（X） 是社区X的熵；（X ｜Y） 是社区X相对于社区Y的条件熵。

的值域为［0，1］，其值越大，说明算法A得到的社区划分还原真实社区划分的程度越高，反之则越低。

真实网络

选取开源的5 种真实世界网络（Karate、Dolphin、Polbooks、Football、SFI）作为社区检测事例。这些网络具有不同规模和分布特征（见表1），可用于测试社区检测方法的性能。 以上5 种算法作用于表1 中每种真实世界网络后，获得的统计结果见表2～表3（注：由于表1 中SFI 的社团数量未知，因此在表3 中各算法不能获得关于SFI 的值；另外，由于NMF 的算法参数设置的特殊性，执行每个网络的社区检测时，每次运行中获得的结果相同）。

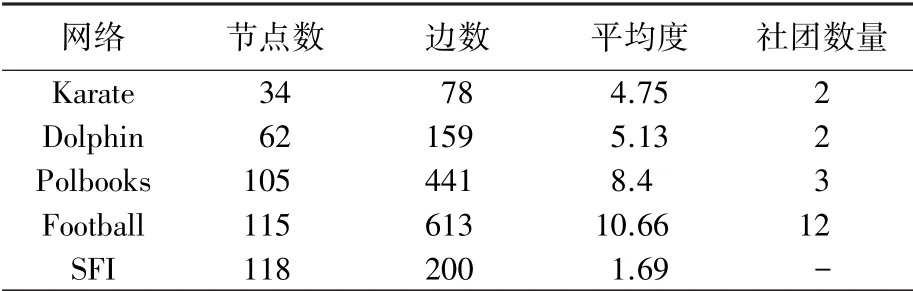
表1 真实世界网络数据Tab.1 Real world network data

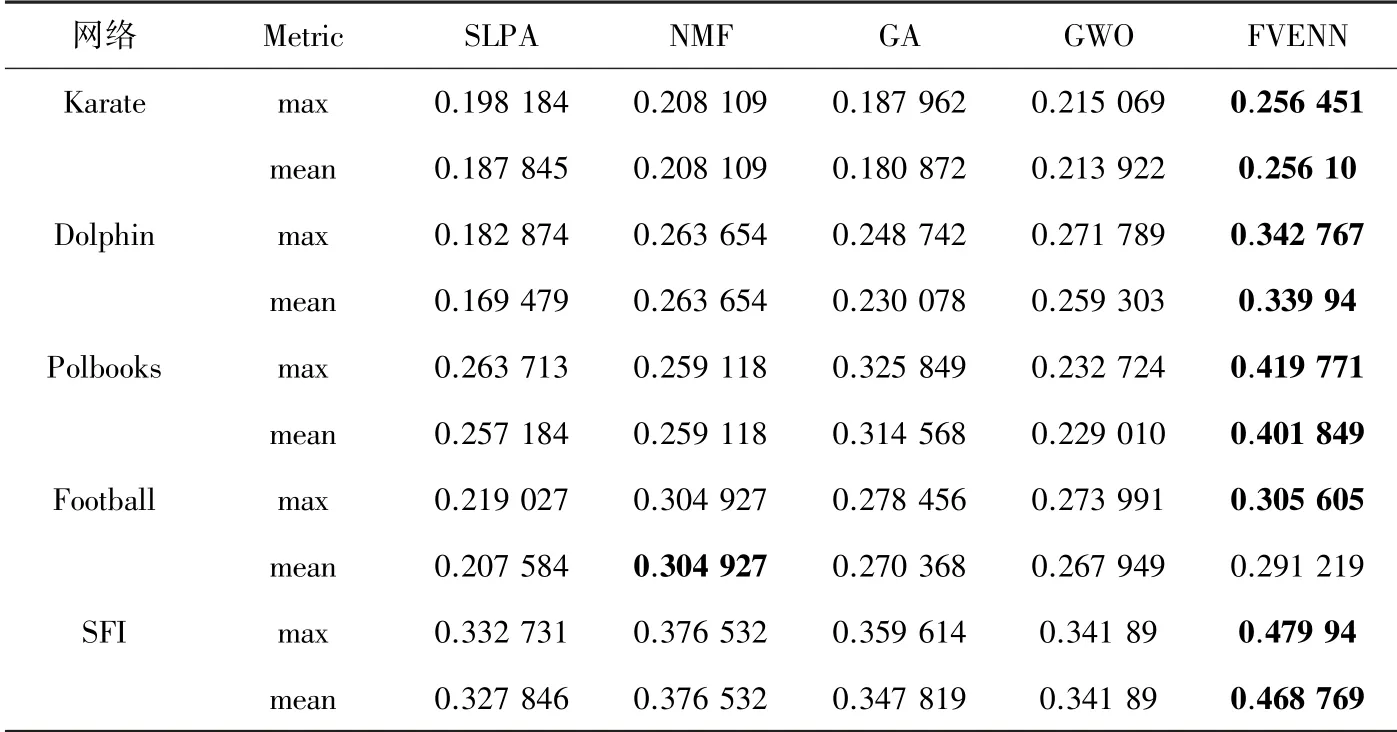
表2 算法作用于真实世界网络得到的IEQ 统计值比较Tab.2 Comparison of IEQ statistics obtained by the algorithm on real world networks

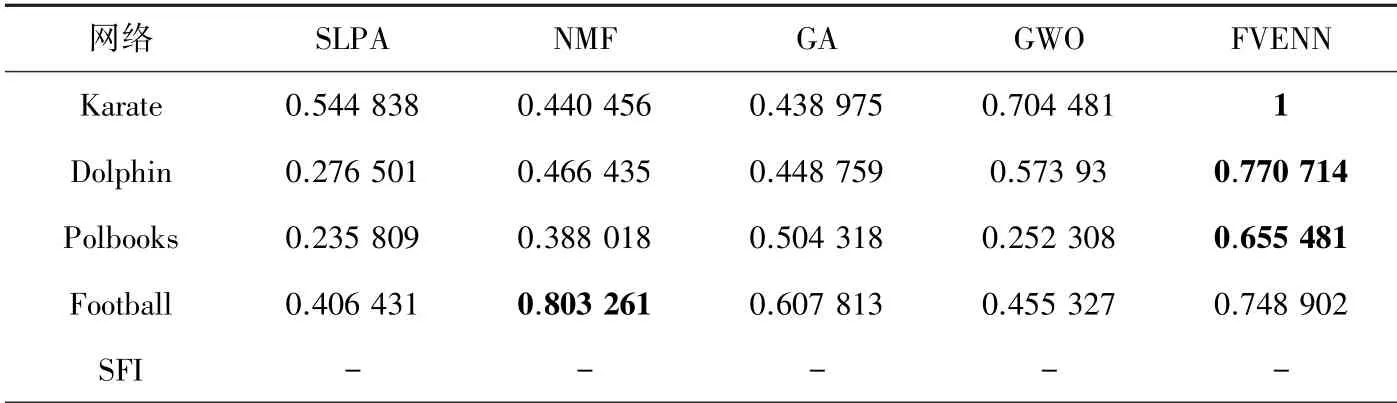
表3 算法作用于真实世界网络得到的ENMI 值比较Tab.3 Comparison of ENMI statistics obtained by the algorithm on real－world networks

由表2 ～表3 获知，对于Karate、Dolphin、Polbooks 及SFI 每种网络中，FVENN 获得的均值、最大值及值，整体上均大于其它算法得到的相应值。 因此该方法的社区检测效果具有明显优势，表明本文的模块度函数作为重叠社区划分指标，能使不同社区之间包含的公共节点较少。 特别是，对于SFI 网络，其网络节点链接十分稀疏，平均节点度数仅为1.69，在此情形下，FVENN 的社区检测优势更加突出。 此外，对于Football 网络，FVENN 的均值比的值略小，但前者得到的最大值比后者明显较大，表明FVENN 经多次运行能得到较好的社区检测方案。 其次，参与比较的4 种算法的社区检测效果并不存在显著差异。 相对而言，的社区检测效果较好；GWO 次之；GA 比SLPA能获得更好的社区检测效果。 因此，表2 说明，智能优化算法应用于社区检测具有较好的潜力。 表3 进一步证实，FVENN 求解Karate、Dolphin 及Polbooks能获得最好的社区检测效果；但在求解Football 时，所获效果略逊色于NMF，其主要原因在于Football网络的实际社区数较大（12 个社区），以及FVENN运行中，初始中心节点的选取具有随机性。

人工合成网络

人工合成网络经由LFR 基准生成，更贴近真实的社交网络，涉及的参数设置与文献［19］中LFR 网络的参数设置相同，即节点数为100；混合参数取01、03、05；重叠成员数O取2、4、6、8；重叠节点数O取01、03；每个社区的最小节点数为5，最大节点数取12；网络节点的平均度数、最大度数分别取10、50；和分别为2 和1。 因此，该人工合成网络由24 个不同规模和特征的LFR 网络构成。

将以上5 种算法作用于这24 个LFR 网络，进而依据指标获得的值与重叠成员数O的关系，如图3 所示。

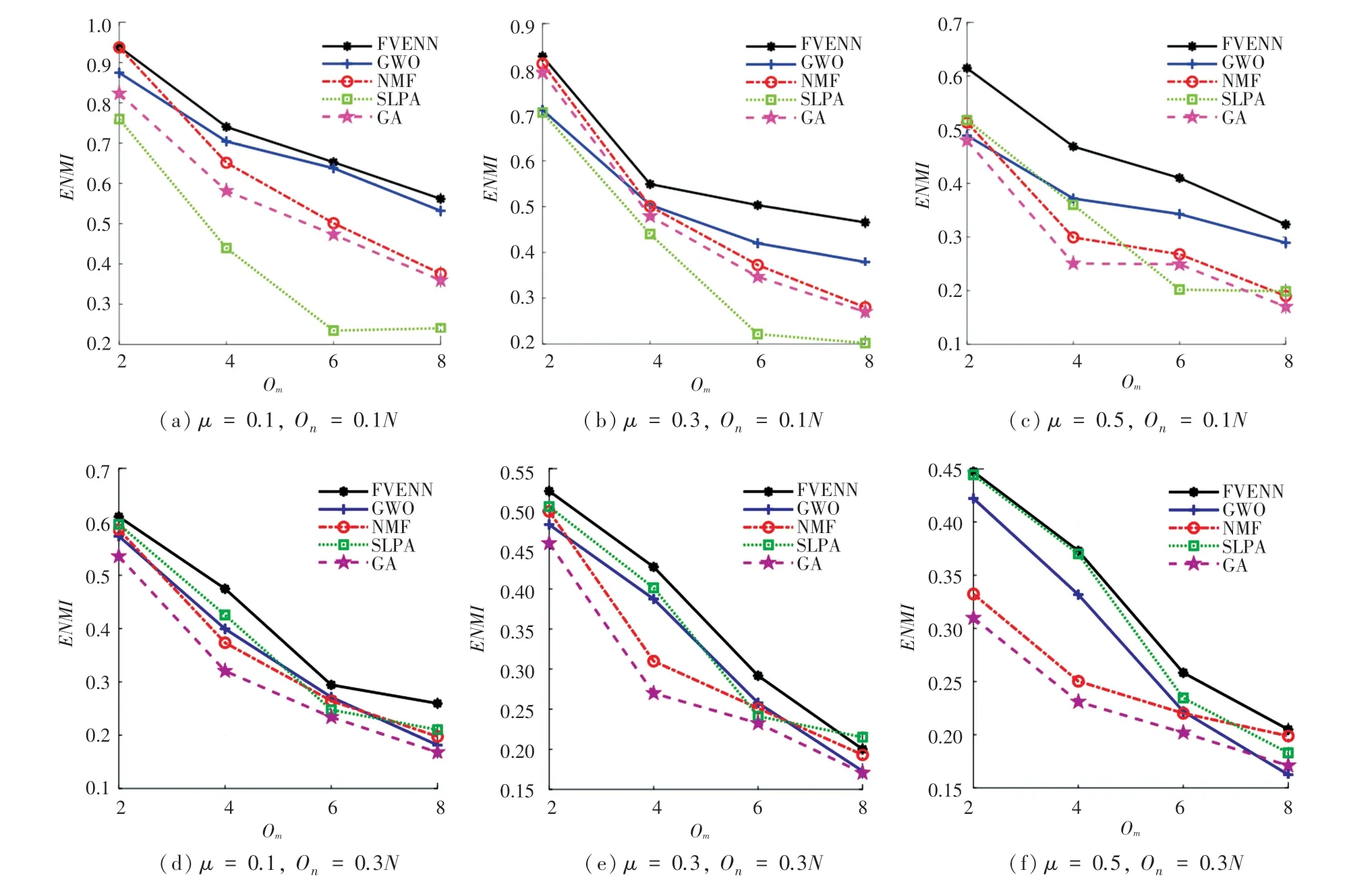
图3 算法获得的ENMI 值随Om变化的曲线比较Fig.3 Curve comparison of ENMI value obtained by algorithms with Om

由图3 获知，在给定的O值下，对于此24 个LFR 网络中的每个网络，FVENN 获得的值，在大多数情况下均比其它算法得到的相应值大，说明该方法的社区检测效果具有明显优势。 尽管在图3（a）和图3（b）中，当O ＝2 时，NMF 与FVENN 获得的非常接近，但随着O的增大，FVENN 的社区检测效果逐渐突出，得到的值比其它算法的值要大。 此外，随着值逐渐增大，各算法得到的值相应变小，但FVENN 的值下降较平缓，且得到社区划分效果的优势更明显。 由此表明，随着LFR 网络的重叠节点数增加，FVENN 的社区检测优势更加突出。

4 结束语

重叠社区检测一直是极为困难的科学与工程问题，探讨如何能恰当刻画重叠社区检测特征的性能指标，以及设计快速求解的优化算法，是社区发现研究中关注的重要科技问题。 本文在设计社区划分的模糊隶属度矩阵基础上，借助模糊分割阈值参数建立能凸显重叠节点对社区检测效果影响的改进型模块度函数，进而将重叠社区检测问题描述为含连续变量的函数优化问题。 随后，利用果蝇视觉系统的信息处理机制，获得改进型果蝇视觉神经网络，并将其输出与灰狼位置更新规则结合，获得果蝇视觉进化神经网络（FVENN）。 比较性实验分析表明，FVENN 求解重叠社区检测问题具有明显优势，搜索效果稳定。 另外，虽然FVENN 检测小规模重叠社区的优势较为突出，但尚未应用于大规模重叠社区的检测问题。 未来研究的重点之一将集中大规模情形下的社区检测模型设计，探讨高效求解的算法。