基于DWT－SVD 鲁棒盲水印算法研究

张 阳， 卿粼波， 何小海

（四川大学 电子信息学院， 成都 610065）

0 引 言

互联网技术的迅速发展，极大的促进了媒体信息的传播，但也让篡改者有机可乘。 针对创作者的版权保护，一种有效的方法是数字水印技术。 数字水印将版权信息嵌入到传输的图像数据中，这些图像数据与嵌入版权信息前肉眼观察无差别，即便篡改者攻击嵌入图像也能大体提取出水印图，能有效保护创作者版权。

现代数字水印技术发展迅速，出现了各种水印算法，传统最低有效位（LSB）算法实现原理简单，透明性好、但鲁棒性差，嵌入水印的图像稍受频率域攻击就无法提取准确的水印。 变换域水印算法的出现大大改善了这一问题。 李文娜等应用离散余弦变换（DCT）算法较为成熟，具有一定的抗攻击性，但DCT 效应导致图像块效应严重，对于原图质量要求高的场景并不适用；以燕鲲鹏研究的分块数字图像水印算法为代表的离散小波变换（DWT）主流算法，对JPEG2000 等有损压缩的攻击具有更强的鲁棒性，但提取水印需要原宿主图或者原水印图，无法实现水印盲提取，其透明性和鲁棒性有进一步提升的空间。 轮廓波（Contourlet）变换在小波变换的基础进一步发展，吴静研究的基于Contourlet变换的图像数字水印算法，相比小波变换有更加优良的抗攻击性，但仍然不能实现盲提取水印，并且对于原图有更高要求。

本文在DWT－SVD 算法研究基础上，通过在不同频段嵌入水印，提取时利用各个频段对原图的估计影响因子进行加权提取，融合成新的水印图。 其中，给各个频段进行奇异值分解，利用奇偶嵌入，将水印的奇偶性嵌入奇异值中，再进行逆奇异值分解（SVD），得到嵌入水印图。 在对原图影响可以接受的情况下，实现了更好的抗椒盐攻击效果，而且实现了水印图像的盲提取。

1 理论基础

1.1 算法框图

传统DWT 加水印算法，如图1 所示。 由于图像能量主要集中在低频部分，传统DWT 算法只将水印低频二阶小波变换低频（LL2）分量信息加入到原图低频LL2 分量，并未考虑水印中存在的高频分量的影响，提取的水印在鲁棒性上存在一定缺陷。 因此，本文将水印高频信息分别加入到原图对应高频分量信息中，算法框架如图2 所示。

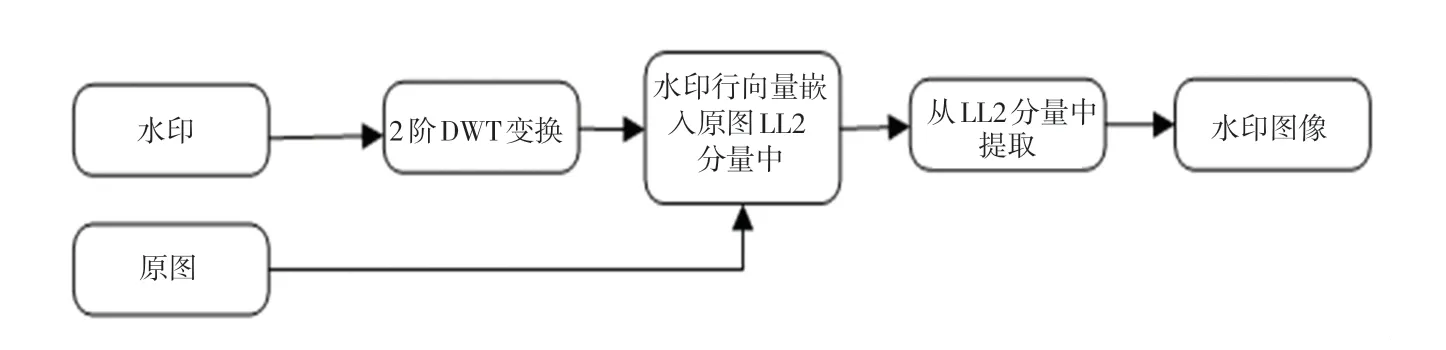
图1 传统DWT 算法Fig.1 Traditional DWT algorithm

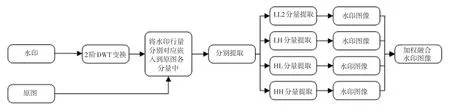
图2 算法框架Fig.2 Algorithm block diagram

1.2 奇异值分解

奇异值分解应用于正交矩阵中，是一种线性代数工具。 矩阵的SVD 分解定义：

、、都是二维矩阵，的大小；的大小；的大小。 奇异值公式（1）。

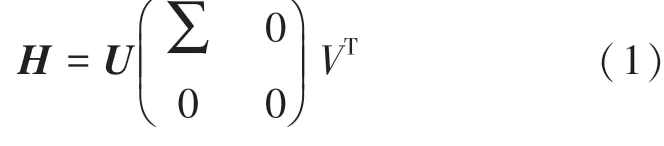
其中，

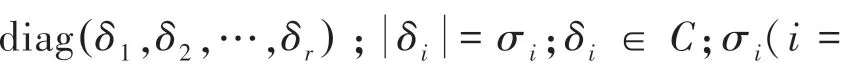
对于二维图像（） 的SVD 分解，公式（2）：

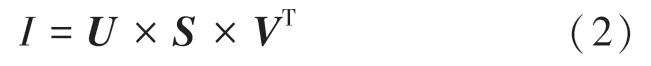
其中，、、都是的二维矩阵，且是奇异值的对角矩阵。

图像的奇异值矩阵具有较好的稳定性，当图像被施加小的扰动，其奇异值变化不大，且在奇异值上嵌入水印不会损害图像的几何特性。 本文取原图二维小波变换后的低中高频8×8 块作奇异值变换，得到矩阵，取（0，0） 作为计算后的奇异值，再嵌入水印值。

1.3 奇偶嵌入

奇偶嵌入的目的是将水印的奇偶性质嵌入原图中，从而可以对已经嵌入图像分析奇偶性，得到水印的值，实现水印盲提取。 本文采用二值图像作为水印图像，奇值为1，偶值为0。 把计算得到的奇异值设为，把二值水印图像的值设为， 嵌入后的值设为，本文通过取整除法Math.floor（20） 计算出原图奇异值的奇偶性，奇偶嵌入对照比见表1。

表1 奇偶嵌入对照表Tab.1 Comparison table of parity embedding

提取水印时根据各频段计算奇异值，判断Math.floor（20） 奇偶性得到原水印图，实现水印图像盲提取。

2 水印的嵌入与提取

2.1 水印的嵌入

实验选用512×512 的灰度图线作为宿主图像，64×64 的二值图像作为水印图像，水印嵌入过程图，如图3 所示。 水印嵌入算法具体描述如下：

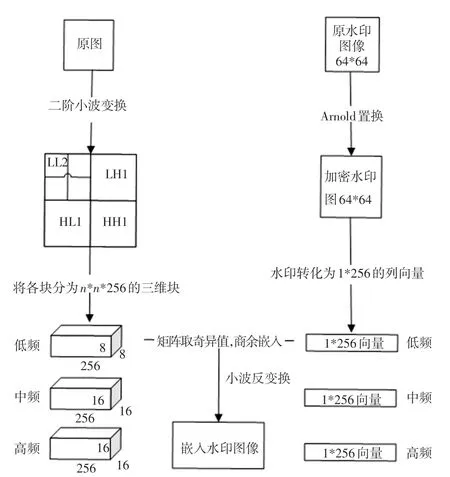
图3 水印嵌入过程图Fig.3 Process diagram of watermark embedding

（1）已求得64×64 矩阵的Arnold 置换周期为48，对原始水印图像置换24 次得到加密的水印图像，并将其转换为一个1×256 的行向量，长度为256；

（2）对宿主图像进行二阶小波变换，分别对LL低频段、LH中频、HL中频、HH高频进行处理，得到各频段的256 三维块，如原图512×512 大小，那么LL可以处理为8×8×256 的三维块，LH、HL、HH 都可以处理为16×16×256 的三维块；

（3）遍历水印行向量，对LL2 低频段取8×8 块（中高频段取16×16 块）求最大奇异值，作为参数，取对应水印位置值，根据表1 计算得到该位置嵌入水印后的奇异值。 对HL1、LH1、HH1 3 个频段的三维块分别采用上述方法进行嵌入处理。 如对HL1频段，假如遍历到第次，对一个16×16 的面进行SVD 奇异值计算，取对角线第一个奇异值，也即最大奇异值作为， 再根据表1 计算得到该位置嵌入水印后的奇异值；

（4）对步骤（3）生成的奇异值进行SVD 逆分解，得到8×8 的面或16×16 的面组成三维块，再分别对应还原为各个频段，最后进行小波逆变换，得到嵌入加密水印的图像。

2.2 水印提取过程

以512×512 的含水印图像进行说明，默认水印是64×64 大小的二值图像，提取水印过程不需要水印原图，水印提取过程如图4 所示。 提取步骤如下：

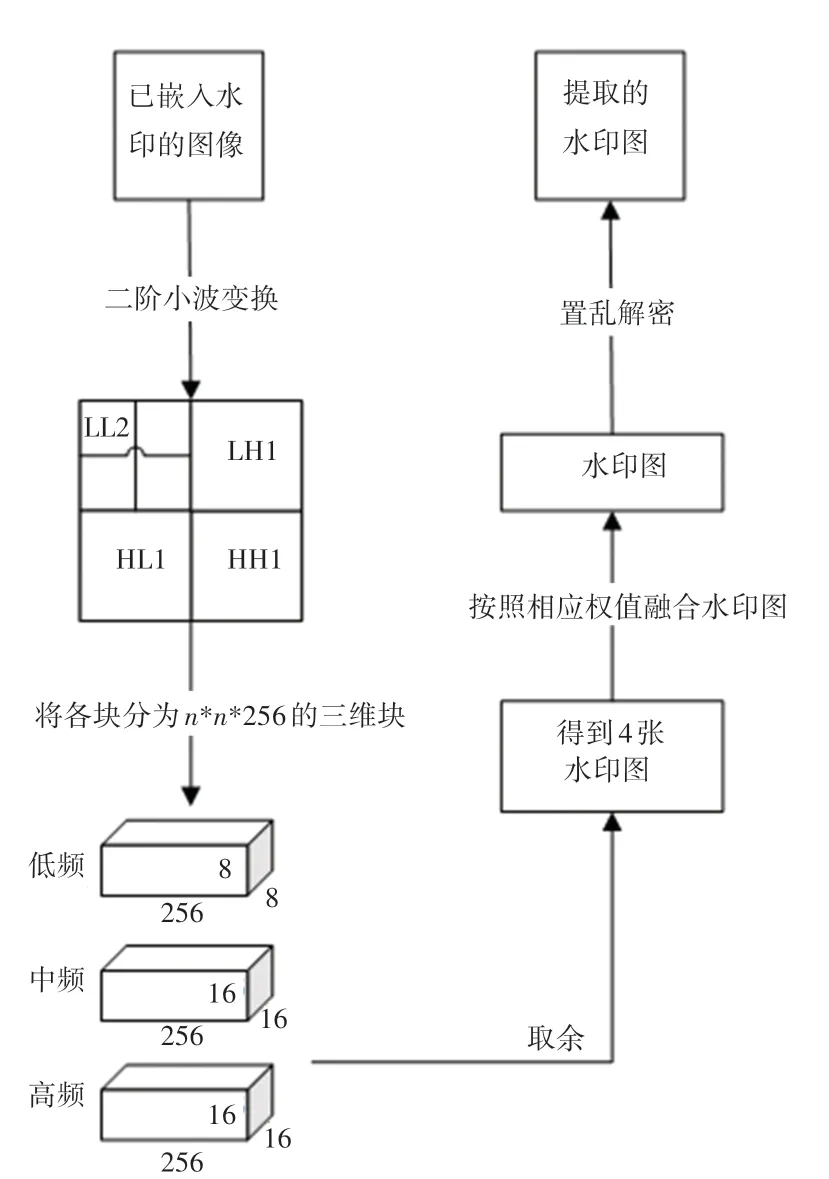
图4 水印提取过程Fig.4 Watermark extraction process

（1）对已嵌入图像进行二阶小波变换，提取出LL、LH、HL、HH4 个频段块，并分别对这些频段块处理为三维块，此例LL可以经处理为8×8×256的三维块，LH、HL、HH都可以处理为16×16×256的三维块；

（2）从1 遍历到256，加入遍历到第次，对每个频段三维块第个面进行奇异值计算，得到最大奇异值，通过取整除法Math.floor（20） 得出水印该位置的值，因此可以得到相应LL、LH、HL、HH4 幅水印图，，，；

（3）按照各个频段加权决定最后水印图，加权水印图计算公式（3）：

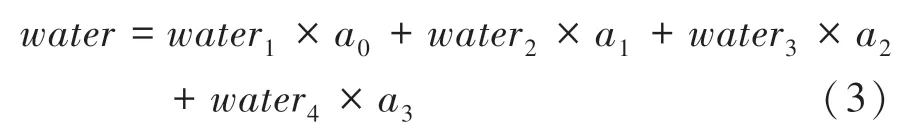
（4）已求得64×64 大小矩阵置乱周期为48，将步骤（3）得到的加密图继续置乱24 次，得到可辨认的水印图。

3 实验结果及分析

实验选取64×64 像素的自制二值水印图像water，512×512 像素 的宿主 图像lenna、barbara、peppers，如图5 所示。 分别对每张图利用3 种不同算法嵌入水印，记录嵌入水印前后的峰值信躁比（） 值；提取水印时，记录提取水印后的归一化相关系数（） 值。

图5 水印原图以及实验原图Fig.5 Original watermarking and experiment

3.1 透明性测试

透明性指水印嵌入后的不可见性，也称为透明性，一般用峰值信噪比（） 来衡量，表示宿主图像的失真情况，其单位为dB（分贝）。 通过均方差（） 进行定义，两个的图像和图像，其均方差定义为公式（4），定义为公式（5）：

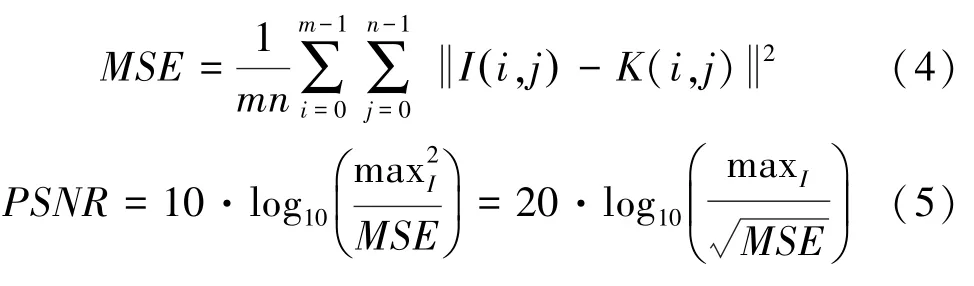
其中，max表示图的图像点颜色的最大值，本文中值为255。

结果表明，利用本文算法嵌入水印后的3 幅图和DCT 变换、DWT 变换、Contourlet 变换＋SVD（简称Contourlet 算法）比较并无太大差异，都满足透明性要求（30 dB），如图6 所示。 分别对嵌入水印后的图进行参数为0.4 的低通滤波攻击、参数为0.03 的椒盐噪声攻击、参数为30 的压缩、参数为1／4 面积的图像裁剪，如图7 所示。

图6 含水印图Fig.6 Image with watermark

图7 被攻击后图像Fig.7 Image after attack

3.2 鲁棒性测试

鲁棒性一般用归一化相关系数（） 衡量，的值越接近1，提取的水印与原始水印越相似，的计算公式（6）：

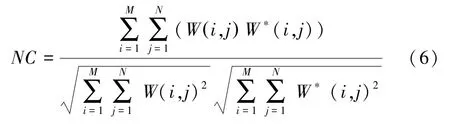
其中，（，） 表示原水印图像，（，） 表示提取出的水印图像。

图7 中被攻击图像利用本文算法提取出的水印如图8 所示。

图8 提取水印图Fig.8 Watermark extraction

实验针对每张测试图，将本文算法与DCT 变换，DWT 变换以及Contourlet 变换作比较，并分别在3×3 模板的低通滤波器下（系数分别为0.4、0.25、0.1）攻击、压缩（质量因子分别为90、60、30）攻击、椒盐噪声（系数分别为0.03、0.02、0.01）攻击，以及图像中间1／4 剪切攻击下对比各种算法的鲁棒性。 测试得到的数值见表2～表4。

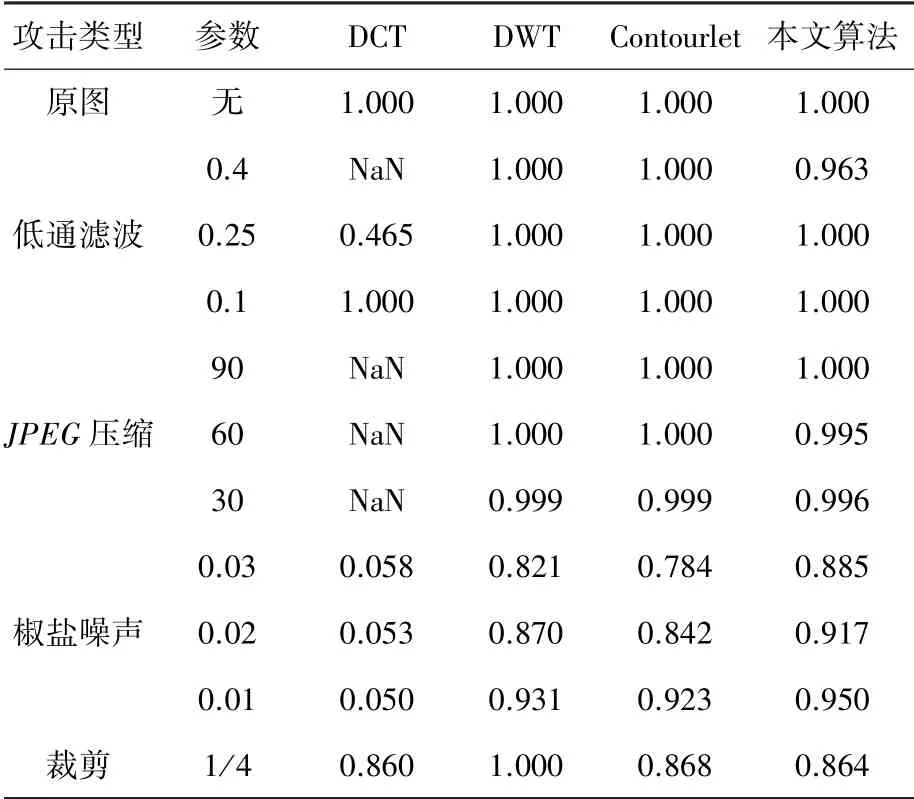
表2 lenna 图提取水印NC 值Tab.2 NC value extraction of watermark from Lenna diagram

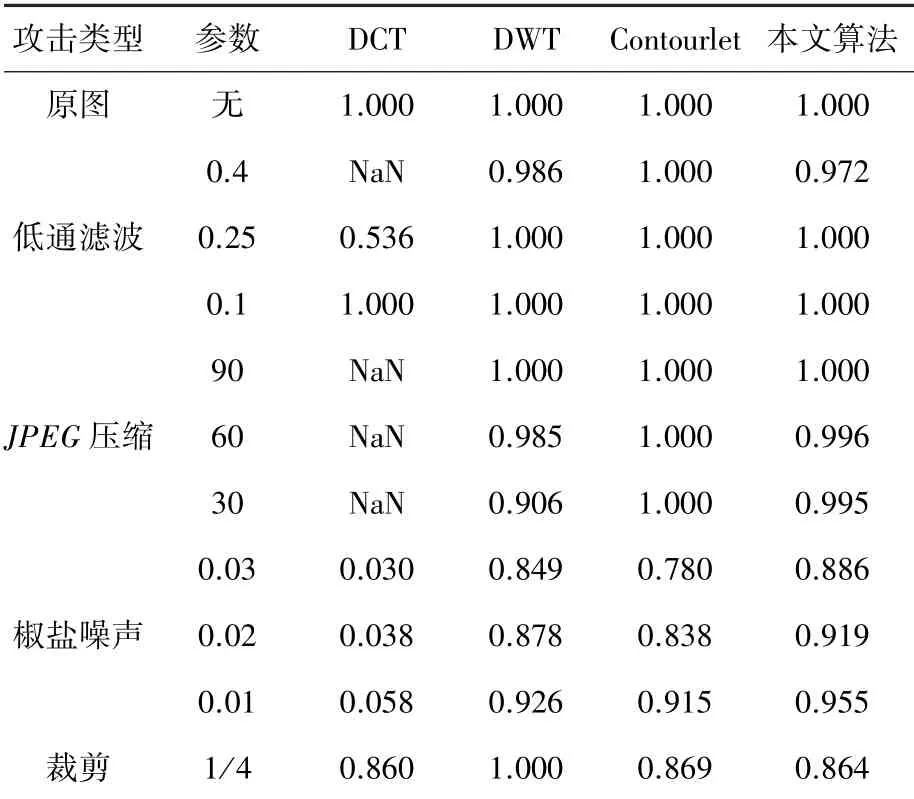
表3 barbara 图提取水印NC 值Tab.3 NC value extraction of watermark from Barbara diagram

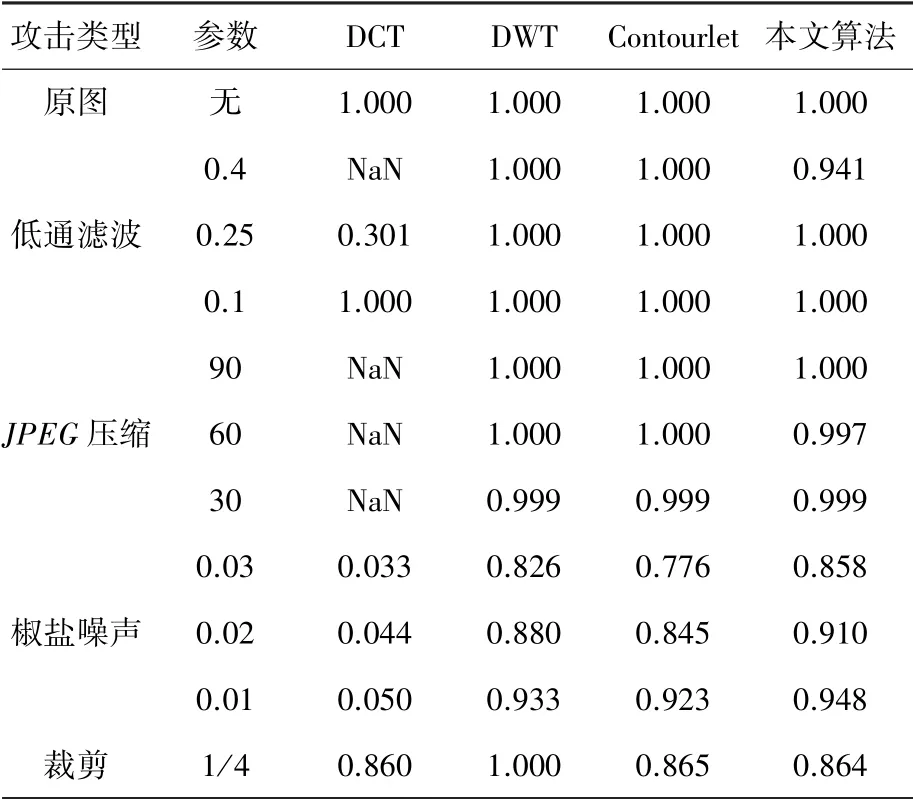
表4 peppers 图提取水印NC 值Tab.4 NC value extraction of watermark from Peppers diagram

3.3 分析

对比各种算法的鲁棒性，通过表2～表4 得知：

（1）不同图片对于算法的测试结果基本无影响，提取水印的值随攻击强度的变化而变化；

（2）低通滤波系数越大，质量因数越小，椒盐噪声越大，都会导致提取水印鲁棒性变差；

（3）DCT 变换算法具有很好的透明性，但水印鲁棒性差，稍加攻击就无法提取水印，另外3 种算法牺牲了适量透明性（但仍然保持30），但水印鲁棒性强；

（4）DWT 变换具有良好的透明性，抗剪切攻击效果优，但面对椒盐噪声攻击，和质量因数较低的压缩攻击，效果不能让人满意；

（5）Contourlet 变换有比较令人满意的透明性和抗攻击效果，但本文算法在透明性相差不大情况下，抗攻击效果略胜一筹；

（6）本文算法在低通滤波，压缩攻击后提取效果和DWT 变换，Contourlet 变换相差不大的情况下，做到了在椒盐噪声攻击下提取效果的提升。

4 结束语

本文提出了一种基于DWT－SVD 鲁棒水印算法，在传统离散小波变换基础上，进行奇异值分解，利用图像奇异值良好的稳定性，提高图像的抗攻击性；在图像奇异值基础上，进行奇偶量化嵌入和提取水印，可实现盲提取；为了进一步提高抗攻击性，在图像的各个频段通过加权融合提取水印。 仿真和攻击实验结果表明，与其它算法进行比较分析，该算法的鲁棒性有一定提高。