含风电消纳的综合能源系统稳定性分析

王东风，陈江丽，李 杰，黄 宇

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引言

综合能源系统是未来能源利用的主要承载形式。与传统的能源单级利用形式相比，综合能源系统能够对多种形式的能源进行多级利用，在提高能源利用率、促进可再生能源规模化开发与就地消纳以及实现节能减排目标等方面具有重要实践意义[1]。化石能源的短缺和污染问题，使得清洁高效的风电资源越来越受关注[2]。风电的接入，会影响综合能源系统运行的稳定；因此，对含有风电等新能源的综合能源系统进行鲁棒分析十分重要。

对不确定性问题的鲁棒分析方法主要有以下几种：随机优化[3,4]、模糊决策优化[5,6]、鲁棒区间优化[7,8]。应用随机优化法时，需要依据不确定输入参数的概率密度函数精确信息进行不确定性建模，所以很难保证计算精度和速度[9]。应用模糊优化方法时，需要依据不确定参数的模糊信息建立模型；该方法计算难度大，并且在模糊信息的描述和方法的选择上具有主观性强、预备工作烦琐的缺点[10]。应用鲁棒区间优化方法时，需要已知风电不确定参数集；在生产实际过程中，该集合容易获得，且模型求解效率高[11]。但是，采用上述常规鲁棒分析方法难以解决综合能源系统设备众多、计算维数较大以及风电强不确定性的问题。

信息间隙决策理论（IGDT）是一种处理不确定性问题的数学优化方法[12]。该方法在使用时不需要已知不确定参数的隶属函数或概率分布函数；在满足预设目标的情况下，该方法能够用来研究不确定参数的变化对系统鲁棒性的影响。目前，IGDT已在负荷需求不确定[13]、价格不确定[14]、新能源[15,16]等诸多领域得到了应用。文献[17]采用IGDT对多源联合优化机组进行了不确定性建模和测试。文献[18]运用IGDT对虚拟电厂调度优化模型中风光出力的不确定问题进行建模并进行测试。文献[19]验证了IGDT在处理机组组合模型中风电不确定问题的有效性。

在解决综合能源系统中风电不确定性的鲁棒问题中，IGDT的应用至今仍较少。为解决上述问题，本文采用IGDT，讨论4种场景下系统的鲁棒性。这4种场景分别为：（1）不含储能单元和燃气轮机，（2）含储能单元，（3）含燃气轮机，（4）同时含有储能单元和燃气轮机。

1 综合能源系统IGDT鲁棒分析模型

1.1 综合能源系统IGDT鲁棒分析模型

综合能源系统包括电网、气网以及相关设备，其主要功能构成有能源输入、能源输出、能源转换器、存储单元和传输线路等。

综合能源系统示意图如图1所示。在该系统中，能源注入以电力和天然气为主，风能为主要低成本新能源。

图1 综合能源系统示意图Fig. 1 Diagram of integrated energy system

风电的接入提高了综合能源系统运行的不确定性，给系统的安全经济运行造成一定困难；因此，需要对综合能源系统进行建模并分析其鲁棒性。

1.1.1 电力网络模型

电力网络的具体模型如下：

式（1）为能量平衡方程，其中：Pg,t，分别为t时段机组和风机出力；Li,t为节点i在t时段的负荷值；，分别为蓄电池充放电功率；Pij,t为t时段支路i-j的传输功率。

式（2）中：Vi,t为节点i在t时段的电压；δi,t为节点i在t时段的相角值；Zij为支路i-j的阻抗；θij为支路i-j的相角值。

1.1.2 天然气网络模型

天然气调节速度较快，可用于调整综合能源系统中不确定风电对系统的影响。天然气网络模型如下：

式（4）为天然气流量平衡方程，其中：fj,i,t为t时段管道i-j天然气流量；Si,t为节点i在t时段的注气量；Gi为节点i燃气最大可供量；ξg,t为该节点的燃气需求量标幺值；Di,t为节点i在t时段燃气轮机的天然气需求量。

式（5）为不可调压力节点的约束条件，其中：ri,t为t时段节点i的压力；Ci,t为与温度、长度、直径、摩擦等相关的管道系数。

式（6）为可调压力节点约束，式（7）为节点i的天然气流量约束，式（8）为节点i的压力限制，其中为节点i的天然气流量和压力的上下限。

1.1.3 储能单元模型

储能单元的数学模型如下：

式（9）为蓄电池荷电状态平衡方程，其中：ηc和ηd分别为蓄电池充电和放电效率；Ei,max为在节点i处蓄电池的最大容量。

式（10）为荷电状态方程，其中：Ei,t为节点i处蓄电池的储能量。

式（13）为蓄电池荷电状态约束，其中：Qi,max和Qi,min为蓄电池荷电最大值和最小值。

1.1.4 机组出力模型

出力机组包含常规机组和燃气机组，其模型主要为气电转换约束以及机组出力限制。具体表达式如下：

式（15）为机组出力爬坡约束，式（16）为机组出力下降速率约束，其中：Rg和Ug为机组的爬坡和下降速率上限。

1.1.5 综合能源系统运行成本分析

综合能源系统运行成本由常规机组发电成本和天然气成本组成，表达式如下：

式中：f1为常规机组发电成本；f2为天然气成本。

常规机组的发电成本通常可用输出功率的二次函数表示：

式中：ag，bg，cg为常规机组的特征参数；Pg,t为t时段常规机组的出力。

天然气成本表达式如下：

式中：Ki为天然气价格系数。

综合能源系统优化运行的目的，是使运行成本在满足用户需求及网络约束条件下达到最小。

1.2 含不确定风电的IGDT鲁棒分析模型

由于系统含有不确定风电，无法使用常规的需要不确定变量概率分布函数或隶属函数的鲁棒分析方法，故采用 IGDT对含不确定风电的综合能源系统进行鲁棒分析。

1.2.1 信息间隙决策理论

IGDT是一种针对含有不确定参数的优化模型求取鲁棒决策的方法，其优势在于不需要知道不确定参数精确概率分布。求解过程中，目标值在可接受范围的前提下，使变量的不利扰动达到最大，从而得到一组鲁棒决策解[20]。解的鲁棒性意味着，当不确定参数在指定范围内任意波动时，如果满足最高预期目标，则该决策解是可行的。

一般情况下，系统的优化模型可表示如下：

式中：f为目标函数值；X为决策变量集合；γ为不确定参数；H(X,γ)和 G(X,γ)为不等式和等式约束。

式中：α为不确定性半径，代表不确定参数的真实值与预测值之间最大偏差。

当输入参数确定时，假设输入参数与预测值相等，可得到目标函数值f0。f0为优化模型的最优解。当输入参数不确定时，优化模型很难求得最优解。为了确保优化效果，决策者需根据需要设定一个最高预期目标值fr。

式中：β为偏差因子，表示确定性模型最优解与预期目标函数值的偏差程度。β越大，决策解对风险的回避程度也就越大。

IGDT定义的鲁棒优化模型表达式如下：

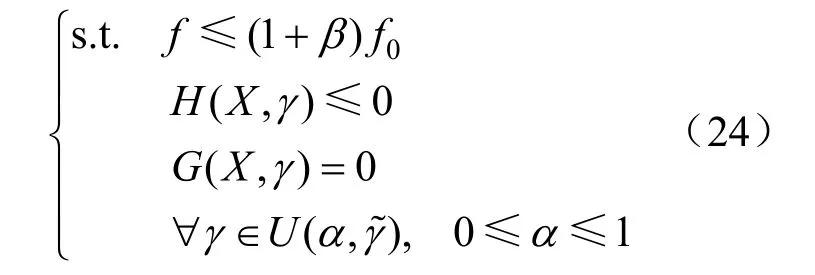
依据上述优化模型，在目标函数值 f不大于预期目标值f0的前提下，最大化不确定参数的波动幅度α，进而求取能够与参数波动抗衡的决策策略。

1.2.2 含不确定风电的IGDT鲁棒分析模型

文中，风电出力为不确定参数，根据式（22），其波动范围可表示为：

在第 1.1节综合能源系统模型中，当风电实际出力低于预测值时，不足以满足负荷需求的功率由其余常规机组或燃气轮机提供，系统总发电成本随之增加。

式中：0≤α≤1。

假设增加后的成本不能高于(1+β)f0，其中β≥0，则优化模型中需要增加如下约束：

在式（27）中，当f≤(1+β)f0时，风电不确定性的不利扰动最大。

鲁棒优化模型如下：

2 算例分析

为验证模型的有效性，采用IEEE-24节点电力网络和20节点天然气网络进行测试，其结构图如图2所示。系统中：共有4个燃气轮机（CGT），其余为常规机组；4个CGT位于1、2、16和22节点。2个储能（ES）单元分别位于19、21节点，最大容量为200 MW和100 MW，其充放电效率分别取0.95和0.9，其余参数可参照文献[21,22]。3个风电场分别接于8、19、21节点，容量分别为200 MW、150 MW和100 MW。

图2 含气电耦合的综合能源系统Fig. 2 Integrated energy system with gas and electricity coupling

在系统中接入天然气网络的情况下，对应的总成本为：f0= $ 907 220.137。

当系统中同时存在ES单元和CGT时，常规机组和燃气轮机发电量如图3所示，储能单元充放电以及存储电量的变化情况如图4所示。

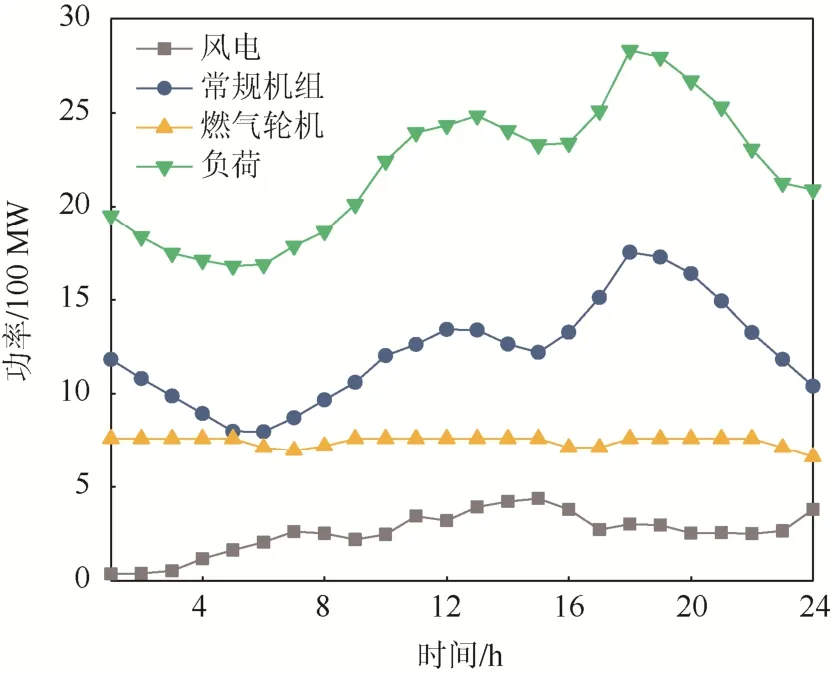
图3 能源供给侧最优出力分布Fig. 3 Optimal output distribution on the energy supply side

图4 储能单元充放电以及存储电量的变化情况Fig. 4 Charge and discharge of energy storage unit and change of stored electric quantity

为研究储能单元和燃气轮机对不确定风电接入综合能源系统鲁棒性的影响，采用式（28）所建模型，分别在表1中的4种场景下进行测试，对比和分析系统的鲁棒性。

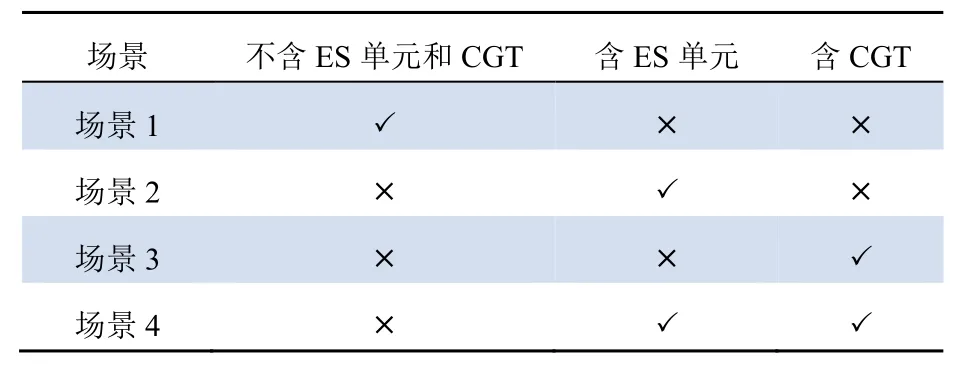
表1 系统鲁棒性分析的4种场景Tab. 1 Four scenarios for system robustness analysis

各场景下的测试结果如图5所示。

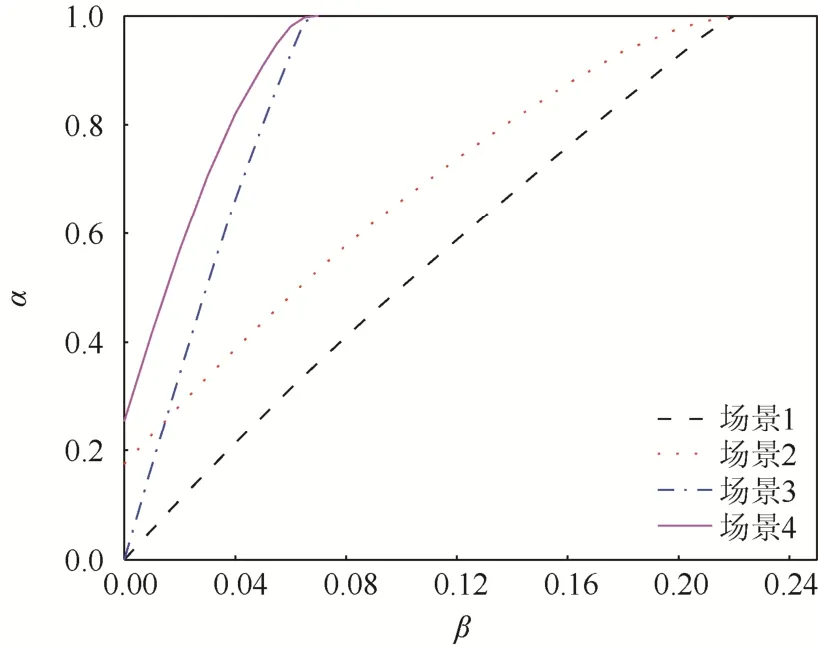
图5 4种场景仿真结果对比Fig. 5 Comparison of simulation results of four scenarios

由图5可知，偏差因子β增大时，α也随之增大，表明系统对风电的消纳能力不断提高。当β相同时，场景2消纳风电的能力强于场景1，原因分析为：ES单元通过电能的储存和释放实现了电能的快速传递，满足了系统为消纳风电而产生的削峰填谷需求，提高了系统的鲁棒性。相比于场景1，场景3对风电的消纳能力更强，原因在于：CGT具有较快的调节速度，可及时调节由于风的不确定导致的系统不稳定情况，减少了不确定风电对系统的影响。

当系统同时接入CGT和ES单元时，与以上3种场景相比，此时系统消纳风电的能力最强。

为证明上述算例计算结果的有效性，图6给出了在场景4情况下，β取值为2%时，风电出力区域S。图6中，S区域为

图6 场景模拟图Fig. 6 Scene simulation diagram

在该区域内随机抽取2 000个风机出力场景，将以上风电场景逐一代入模型中检验并求取对应场景下的发电成本，得到成本的概率分布图如图7所示。

图7 S区域发电成本概率图Fig. 7 Probability diagram of power generation cost in S region

图7中的成本均小于该值，这表明上述决策解具有良好的适应性。

3 结论

针对综合能源系统中加入不确定风电后系统的鲁棒问题，本文建立了数学模型。结论如下：

（1）建立了含不确定风电的综合能源系统的IGDT鲁棒分析模型。该模型权衡了安全性和实用性，同时考虑了电力网络、天然气网络以及网络之间的耦合交互。

（2）采用IGDT分析系统鲁棒性。在综合能源中“不存在储能单元和燃气轮机”“存在储能元件”“存在燃气轮机”和“同时存在储能元件和燃气轮机”这4种不同场景下对风电的消纳能力进行评估。

算例结果表明：系统中同时存在储能单元和燃气轮机的场景下，当风电出力这个不确定参数不超出计算所得值时，系统能保证预期目标不差于某个最低预设结果。所以，储能单元和燃气轮机的介入，提高了系统对风电的消纳能力，系统的鲁棒性增强。