基于改进型相似度的协同过滤算法的研究
2022-05-10吴锦昆单剑锋
吴锦昆,单剑锋
(南京邮电大学 电子与光学工程学院、微电子学院,江苏 南京 210023)
0 引 言
在大数据时代,每个个体在日常生活上网产生的一些行为,都会生成大量的数据。这些数据对于互联网平台来说是描述用户的重要信息来源,再利用这些数据结合利用协同过滤算法,能够促进互联网平台的高效运行。当人们处在面对大量的信息与平台推送各种各样的短信时,要从海量的信息中获取有用的信息是困难的,面对海量的信息更是一个令人头疼至极的问题。所以大数据被运用的场合越开越普遍,抖音、拼多多、淘宝等这些互联网平台都会根据用户的历史行为以及对产品的偏好,来对用户进行个性化、精准化推荐,给用户带来更加良好的体验。
不论是基于用户还是基于物品的协同过滤算法,数据总是存在稀疏性的问题。文献[1]中利用随机性对原有的用户-商品评分矩阵进行填充再进行矩阵变换,文献[2]提出挖掘用户的相关信息,文献[3]提出利用BP神经网络来预测用户的评分,从而改进数据集稀疏性的问题。文献[4]中考虑用户的偏好以及物品的内在属性从而改进相似度计算,改进了协同过滤算法相似计算。文献[5]提出了一种融合型余弦相似度计算方法,其中包含了相似度修正参数和基于用户属性的特征向量,解决了用户之间不同评价体系和用户的不同属性的问题。文献[6]提出了一种全新的相似度计算方法,利用两个用户对相同物品的评价的比值作为相似度计算的依据,使提出的协同具有更高的精确度和较低的平均绝对误差。文献[7]利用项目的标签及评级信息,引入了时间加权因子来解决数据的稀疏性的问题。文献[8]根据不同用户的评分范围,将用户分为正常、严格、宽裕和中间四种,提出了基于标准差比例的改进和统一的基线改进模型,以便消减经典基线估计模型的局限性。文献[9]根据Translation-based模型在稀疏的数据集上的良好表现,将这种模型与递归神经网络模型进行融合,提出了Recurrent Translation-based Network模型。文献[10]采取随机梯度下降法优化了矩阵分解,结合谱聚类方法填充方法,有效降低了数据的稀疏性对于准确性的影响。文献[11]采用主成分分析法,对用户-项目评分矩阵进行降维,再对K-means算法进行改进,提高了聚类的速度,有效提高了准确率和召回率。
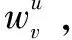
1 协同过滤算法
现今,协同过滤算法大致分为三类:一类是基于用户的协同过滤算法,一类是基于物品的协同过滤算法,还有一类是基于模型的协同过滤算法。
协同过滤算法被广泛应用于人们日常生活的方方面面。例如音乐、电影、网购等。为了使用户能够更加迅速地浏览与自己偏好相关的音乐、视频、商品,各个平台都在寻找更加适合平台的推荐算法,给用户带来极致的体验。
协同过滤算法,主要功能是找出与某一用户相似的用户,将相似用户的所评级或消费的商品推荐给这个用户;或者根据用户历史消费过的商品,推荐给用户相似的商品[12]。分别是基于用户的协同过滤算法和基于物品的协同过滤算法。
1.1 相似度计算
在传统的协同推荐算法中,计算相似度的方法主要有两种:皮尔逊相似度、余弦相似度。该文主要针对协同过滤算法中的皮尔逊相似度计算进行改进。皮尔逊相似度计算公式如下:
(1)
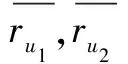
余弦相似度类似于求两个向量形成夹角的余弦值,根据用户对电影的评分形成空间向量[13],计算空间向量形成夹角的余弦值,确定不同用户之间的相似度。
余弦相似度计算公式如下:
(2)
(3)
式中,I,U分别表示u1,u2评价过的项目的交集,对i1,i2评价过用户的交集。相较于皮尔逊相似度,余弦相似度中没有考虑到用户评价的平均分,忽略了用户自身带有的评价体系。
1.2 协同过滤算法准确度的评价准则
准确度的评价指标,是衡量协同过滤算法准确度的一个重要方面。选取合适的评价指标能够很好地衡量算法改进前后的效果。文献[14]中,详细阐述了推荐系统中的各种评价指标,从预测评分的准确度上有平均绝对误差、均方根误差,根据最终的平均绝对误差值的大小,从而确定算法的优劣,得到的平均绝对值较小的协同过滤算法推荐的准确度较高。从分类的准确度上有准确率、召回率,还有一些其他评价指标,深入分析与比较各个指标之间的差异。该文采用平均绝对误差(MAE)来衡量改进相似度计算后的推荐算法的性能。
1.2.1 平均绝对误差
平均绝对误差是最经典的计算真实评分与预测评分的差异。表达式如下:
(4)
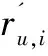
1.2.2 均方根绝对误差
均方根绝对误差,是将绝对误差求平方之后,再求平方根。表达式如下:
(5)
2 改进的相似度计算方法
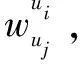
sim(u1,u2)=
(6)
(7)
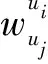
皮尔逊相似度改进前与改进后的相似度计算结果比较:
在表1中,存在4个用户,分别对四个物品都进行了评分,依据式(1)可以计算出用户之间的皮尔逊相似度,计算结果如式(8)~式(11)所示。
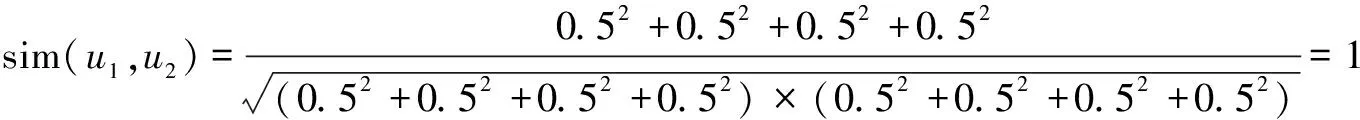
(8)
(9)
(10)
(11)
用户u1,u2,用户u1,u3以及用户u1,u4的相似度都为1,可以判断出用户u1,u2,u3,u4之间具有相同的相似度,但是从用户u1,u2,u3,u4对电影的评分的不同可以看出他们之间的相似度应该有一定的差异,可以从表中的数据判断出用户u1,u2之间的相似度应该高于用户u1,u3之间的相似度,用户u1,u4之间的相似度应该高于用户u1,u2和用户u1,u3之间的相似度,而不是四者之间具有相同的相似度。
为了解决上述计算结果中用户之间存在差异不明显的问题,引进用户差异因子来区分用户,改进后的皮尔逊相似度计算过程如式(12)~式(15)所示。
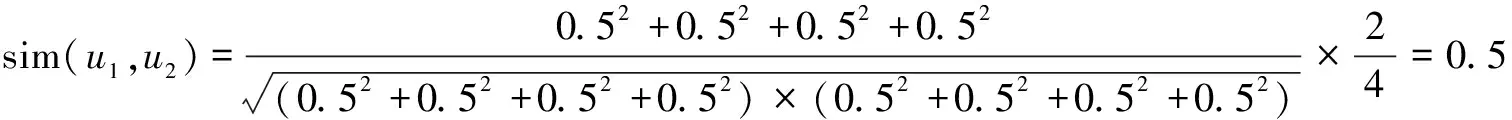
(12)
(13)
(14)
(15)
用户u1,u2之间的相似度为0.5,用户u1,u3之间的相似度为0.4,用户u1,u4之间的相似度大约为0.67,用户u2,u3之间的相似度为0.8,可以看出改进后的相似度计算方式得出用户u1,u2,u3,u4之间具有不同的相似度。经过改进后的皮尔逊相似度得到的计算结果表明,引入用户差异因子改进的皮尔逊相似度计算方式,更加能够体现出不同用户之间的差异,能够对之前相似性较高的用户进行更加精细的区分。
表1 不同用户对已购商品的评分
3 实验步骤及结果分析
3.1 实验步骤
仿真过程建立在Spyder平台上基于Python3.8版本进行,主要建模仿真步骤如下:
(1)导入相关实验相关的Movielens 1m相关数据集。每一次都将数据集按照7∶3的比例划分为训练集和测试集,经过三次得到不同的测试集与训练集,部分数据集如表2 所示。
(2)构建用户-项目评分矩阵,分别采用皮尔逊相似度与改进后的皮尔逊相似度计算公式,来计算用户之间的相似度。
(3)根据计算得到的相似度,选择邻居个数,预测用户对测试项目的评分。
(4)根据预测得到的评分计算MAE值。
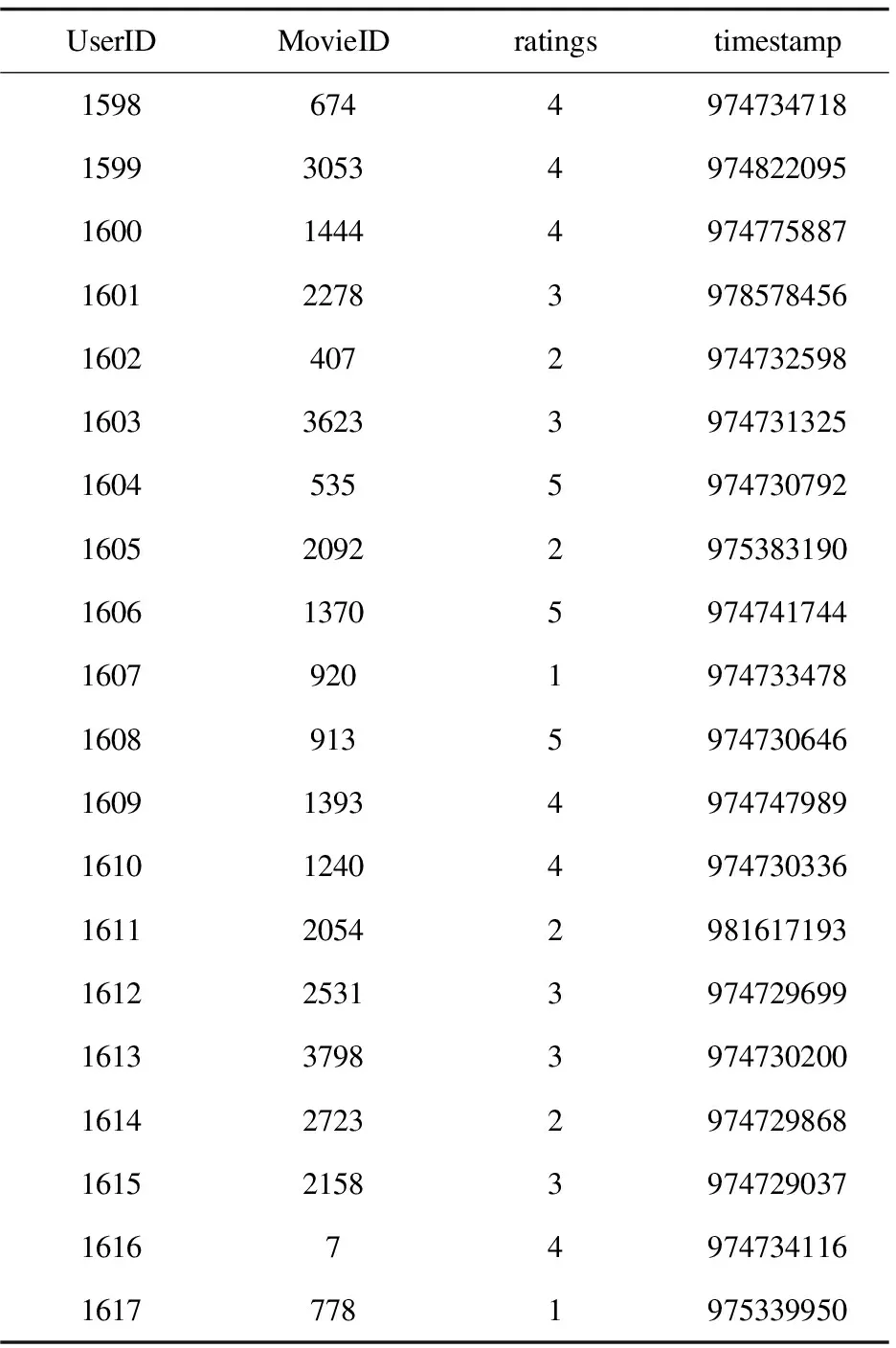
表2 Movielen 1m部分数据集
在表2中UesrID代表用户编号,MovieID代表电影编号,部分电影编号对应的电影如表3所示,ratings代表对应的用户给对应电影的评分,timestamp代表时间戳,即用户对电影评分的时间。

表3 部分电影编号与对应电影
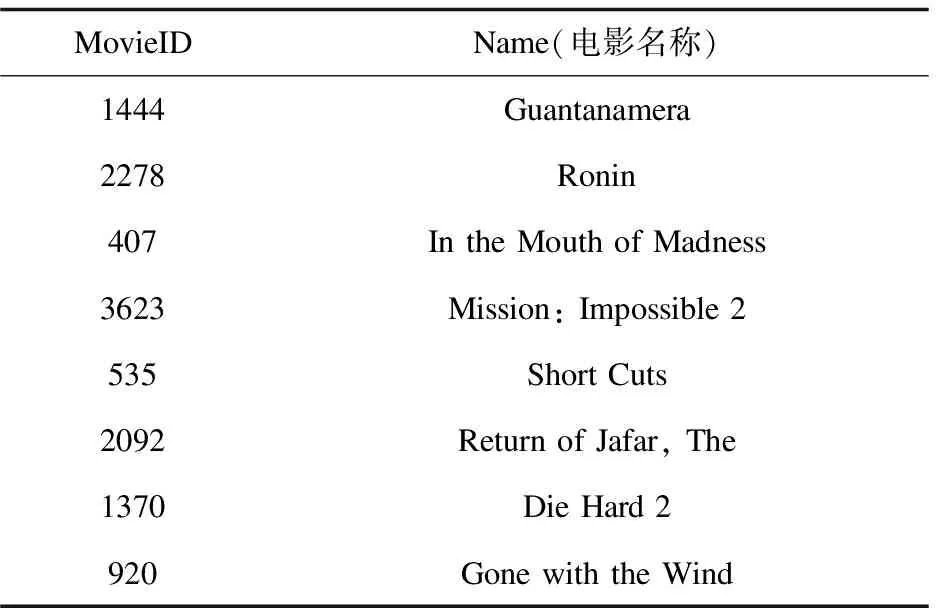
续表3
3.2 实验数据集介绍及数据集处理
该文采用的数据集来自Movielens数据集中的ml-1m数据集。目前主要的协同过滤算法基本上都采用Movielens类数据集。在ml-1m数据集中包含了3 952部电影,6 040个用户,评分在1~5之间。将数据集划分为训练集和测试集,训练集用来计算用户之间的相似度,测试集用来根据训练集计算出的相似度进行预测评分[13]。
3.3 实验结果及分析
对于最近邻数分别选取k=25、50、75、100,根据划分不同的训练集与测试集分别进行3次仿真实验,对同一次划分的训练集和测试集,先用改进前的协同过滤算法进行仿真,然后用改进后的协同过滤算法对划分好的数据集进行仿真,仿真后得到MAE值,然后再对三次得到的MAE值求平均值,以消除仿真得到的MAE值存在一定的偶然性误差。经过仿真实验得到不同的最近邻数的结果分别如表4、表5所示。
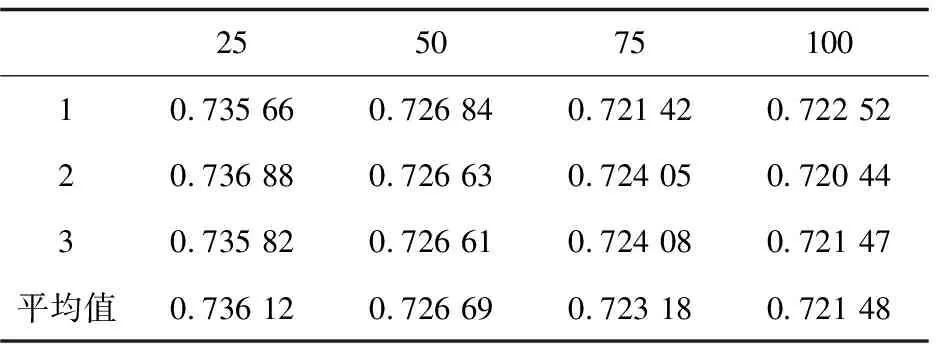
表4 算法改进前MAE值
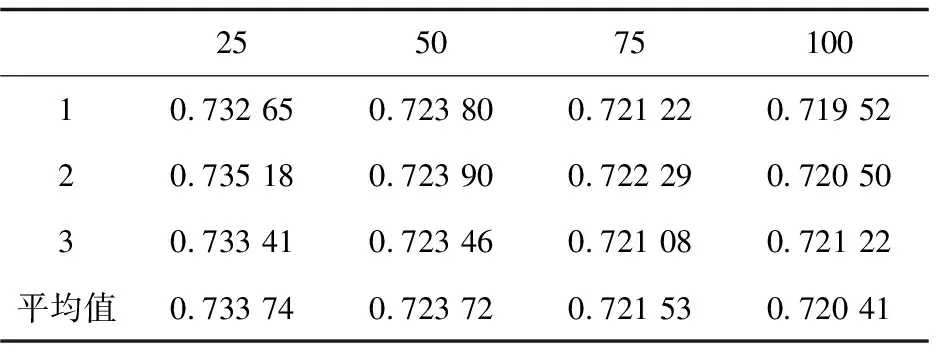
表5 算法改进后MAE值
根据表4、表5中的第四行中的平均值,得到的MAE平均误差曲线如图1所示。
从图1中可以看出,改进后协同过滤算法的平均MAE值基本上都低于改进前的平均MAE值,在近邻k值选取较小的值时,MAE值下降比较明显,特别是在最近邻数k选取50时,MAE值有较大的下降。在近邻k取较大值,由于选取的近邻k值较大,会降低协同过滤算法相似度计算的作用,导致MAE值并没有明显的下降。改进后的算法在最近邻数k选取较大时,效果不够明显,也是未来算法改进的一个方向。
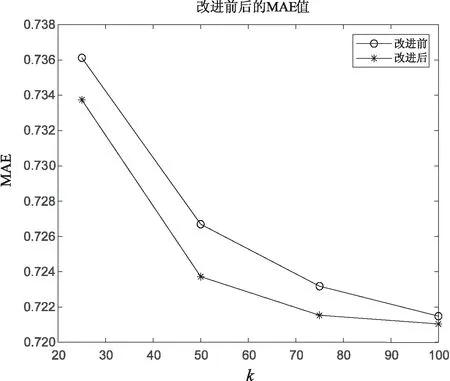
图1 改进前后MAE值曲线
4 结束语
因为传统的协同过滤推荐算法在皮尔逊相似度计算中只考虑用户之间的线性关系和用户的平均分,没有考虑到每个用户更加深层次的评价体系,用户本身的评价体系会对用户对商品的评分产生一定的影响,所以在利用皮尔逊相似度计算用户之间的相似度时会出现一定的误差。
该文考虑到用户的评分最大值可能一定程度上构成了用户评价体系的一部分,提出了一种改进型相似度的协同过滤算法,即引入了用户差异因子,改进了原有的相似度计算方式,在相似度计算中,能够起到一定的区分用户的作用,因此能够得到较为准确的相似度,从而提升推荐的准确度。
根据在Spyder平台基于python3.8仿真后得到的数据表明,引入用户差异因子后的改进型皮尔逊相似度计算方式能够降低平均绝对误差(MAE),可以说该改进型协同过滤算法在准确度方面的性能有一定的提升。但是当邻居个数(k)选取较大时,MAE值没有较大的改善,未来值得进一步探讨。
尽管经过改进后的协同过滤算法改善了传统的协同过滤推荐算法忽略每个用户拥有各自的评分差异,但是依然存在一些问题。首先,该算法增加了一定的计算量,提升了计算的复杂度;其次,没有解决协同过滤算法存在的冷启动问题;最后,将数据集划分为测试集与训练集并没有解决ml-1m数据集中存在稀疏性的问题。因此,改进的协同过滤算法仍然需要进一步的完善。
