改进人工鱼群法的机器人路径规划方法
2022-05-10陈茜茜张秀峰
张 宁,陈茜茜,李 微,张秀峰*
(1.国家康复辅具研究中心,北京 100176;2.天津理工大学 电气电子工程学院,天津 300384)
0 引 言
机器人是将电子技术、控制技术、机械技术以及通信技术等技术融合为一体的高科技学科[1],机器人的诞生节省人类大量财力、物力,提升社会生产效率,人类无法完成的高危任务通过机器人可顺利完成。导航机器人是机器人领域的重要课题。依据机器人规划目标存在的差异,可将机器人路径规划分为全区域遍历路径规划以及点对点路径规划两部分[2-3]。可视图法、栅格法等方法可应用于环境已知情况下的路径规划,粒子群算法、遗传算法等机器学习算法可应用于未知环境以及仅明确部分环境情况下的路径规划。
目前针对机器人路径规划的研究较多,徐小强等人分别利用改进人工势场法以及萤火虫算法实现机器人路径规划[4-5],但对于障碍物过多以及动态环境下,规划性能较差。人工鱼群法是依据动物行为而来的全局寻优的重要方法,人工鱼群法依据动物的局部寻优行为获取群体的全局最优值,该算法具有较高的全局收敛能力,可有效避免计算过程中陷入局部最优,自适应搜索能力强,无需设置目标函数梯度值即可实现算法快速收敛[6]。针对机器人路径规划问题对人工鱼群法实施改进,为提升机器人路径规划性能,获取最佳全局极值能力,改善传统人工鱼群法对启发式函数起始点要求过于迟钝的缺陷,利用自适应拥挤度因子以及自适应视觉范围对人工鱼群法实施改进,提升机器人路径规划有效性。通过实验验证采用改进人工鱼群法规划机器人路径具有较高有效性。
1 改进人工鱼群法的机器人路径规划方法
1.1 建立环境模型与路径表示
选取多面模型表示法建立机器人行驶路径的环境空间模型。设所建立的环境空间未考虑高度信息,机器人移动范围为二维有限空间,将机器人半径的一半向外扩展设置为障碍物边界[7],保障障碍物与机器人间存在一定距离,将机器人视为移动质点。
在直角坐标系XOY内建立全局环境场景,利用圆或实心多边形表示障碍物,用Z(xz,yz)与T(xt,yt)分别表示起始点以及目标点,利用x轴以及y轴设置为连接Z与T的直线以及垂直于x轴且经过Z的直线,获取新的环境坐标系xoy。坐标变换直角坐标系XOY内随机点Q(X,Y)可得该点在坐标系xoy内的坐标为:
(1)
(2)
式中,λ与(x,y)分别表示初始x轴与ZT间的夹角以及点Q在坐标系xoy内的坐标。
n等分线段ZT,用{L1,L2,…,Ln-1}表示沿各等分点所获取的与ZT垂线段垂直的栅栏线。随机选取栅栏线中点设置为路径节点,可得y={ys,y1,y2,…,yn-1,yt}即不同路径节点纵坐标向量建立的环境空间路径。
机器人路径规划结果由所建立目标函数决定,选取机器人行驶路径总长度最短以及路径安全度最高作为优化目标[8],将机器人行驶路径依据障碍物碰撞情况分为不可行路径以及可行路径两部分。利用惩罚函数法获取目标函数值极小的个体,利用施加惩罚项在评价不可行路径时提升目标函数值。设包含起始点以及目标点的路径节点数量为n,该路径中包含路径段数量为n-1,用Q={Q1,Q2,…,Qn}与Qi(i=1,2,…,n)分别表示路径以及路径节点。建立优化目标如下:
(1)路径总长度最短。
(3)
式中,|qiqi+1|与num分别表示路径段qiqi+1长度以及路径Q内相交于障碍物的路径段数量;inf1表示路径Q为不可行路径时所需施加的惩罚项。
(2)路径安全度。路径安全度指机器人行驶过程中需躲避障碍物,避免碰撞障碍物,设置机器人路径规划路径安全度目标函数如下:
(4)
式中,g与μ分别表示路径Q与全部障碍物的最短距离以及保障路径安全度有界的合适正数;num与inf2分别表示与障碍物相交的路径Q内路径段数量以及路径Q为不可行路径时所需施加的正数惩罚项。
选取权重系数法建立多目标机器人路径规划的目标函数,将总目标函数值分配权值至各目标函数值[9],建立机器人路径规划总目标函数表达式如下:
f(Q)=ω1·f1(Q)+ω2·f2(Q)
(5)
式中,ω1表示路径长度的权值系数,ω2表示路径安全度的权值系数。
可依据机器人行驶场景以及路径规划需求实时调整权值系数[10],获取最优机器人路径规划结果。利用改进人工鱼群法求解所建立总目标函数,规划机器人最佳行驶路径。
1.2 人工鱼群法
令向量X={x1,x2,…,xn}表示人工鱼群法中个体状态,xi为待寻优变量。Y=f(x)与di,j=‖Xi-Xj‖分别表示人工鱼个体当前位置的食物浓度以及不同个体间距;Y与Visual分别表示目标函数值以及人工鱼感知距离;step与δ(0<δ<1)分别为人工鱼移动步长以及拥挤度因子。
人工鱼群法主要包括以下操作:
(1)觅食操作。Xi表示人工鱼个体此时状态,随机选取状态Xj于感知范围内,采用人工鱼群法求解极小值时,当Xi>Xj以及Xi≤Xj时,分别向Xj方向前进以及再次随机选择状态Xj,重复判断状态Xj是否符合移动条件,重复迭代仍不符合移动条件时,继续向随机方向移动[11]。

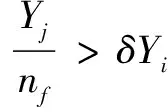
(4)公告板。人工鱼群内最优人工鱼个体状态利用公告板存储。人工鱼群法中人工鱼个体完成寻优操作后应查看公告板所登记状态与人工鱼个体状态[12],人工鱼个体状态优于公告板状态时,更新公告板。
(5)操作选择。依据机器人路径规划需求评价人工鱼环境,依据人工鱼个体环境选取相应操作。机器人路径规划问题是极小值求取问题,需令人工鱼进行追尾操作,追尾操作无法进步时需进行觅食操作[13],觅食操作无法进步时需执行聚群操作,以上操作仍未获取理想结果时,令人工鱼个体随机选取操作。
1.3 改进人工鱼群法的机器人路径规划
利用自适应拥挤度因子以及自适应视觉范围对人工鱼群法实施改进。
通过栅格法将所建立环境空间实施离散化,用(xi,yi)与h分别表示人工鱼i的当前位置以及评价函数,(xg,yg)表示待求解目标点位置,可得评价函数h如下:
(6)

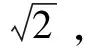
采用人工鱼群法规划机器人路径时,利用觅食、追尾、聚群操作用于寻优以及收敛[14],默认人工鱼群进行觅食操作,用nra表示跳转因子,人工鱼群通过nra次觅食操作后转化为追尾操作以及聚群操作。
1.3.1 自适应拥挤度因子以及自适应视觉范围
人工鱼群法的视觉范围过大以及过小时,分别有利于全局寻优以及局部寻优。将视觉范围设置为先大后小,提升人工鱼群法的计算效率。利用拥挤度因子求解最小值问题,设置拥挤度因子较小[15],令人工鱼个体较分散;计算后期时,设置较大的拥挤度因子,聚集人工鱼至最优点,完成拥挤度因子以及视觉范围自适应,可得公式如下:
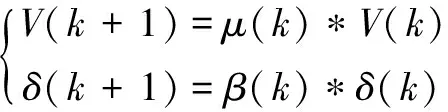
(7)
式中,V(k)与μ(k)分别表示视觉范围及其自适应调整因子;δ(k)与β(k)分别表示拥挤度因子及其自适应调整因子。用j表示调整次数,可得视觉范围以及拥挤度因子自适应调整公式如下:
(8)
(9)
利用以上公式实现觅食操作视觉范围的自适应调整,令视觉范围在追尾操作以及聚群操作中维持不变。
1.3.2 改进人工鱼群法
利用改进人工鱼群法实现机器人路径规划具体流程如下:
(1)参数初始化。用V与N表示视觉范围以及鱼群规模,M与T表示算法迭代次数以及操作选择尝试次数,s=0与δ(0)分别表示人工鱼个体移动步数以及拥挤度因子初值,lengbest=∞与n=0分别表示最优路径长度以及次数计数,nra与pathk分别表示跳转因子以及路径规划表,pathbest表示所需获取的机器人最优行驶路径。
(2)将路径起点gbegin添加至路径规划表pathk内。
(3)人工鱼个体k满足s=nra时,形成随机数ra=rand(2);ra=0与ra=1时,分别执行群聚操作以及追尾操作;s≠nra时,令该人工鱼个体实施觅食操作。
(4)设置k=k+1,当k=N时,令人工鱼群内全部人工鱼个体前进。设置s=s+1,观察目标点gend处是否存在人工鱼,观察结果为存在时,设置k=0,将此时路径长度lengk输出。输出路径长度小于最佳路径长度时,此时所输出路径更新为最佳路径,此时pathk输出为pathbest,进行步骤(5);否则转回至步骤(3)。
(5)设置n=n+1,当迭代次数满足所设置次数时,终止改进人工鱼群法计算,否则转回至步骤(2)。
2 实例分析
为验证所研究方法对于机器人路径规划的有效性,建立大小为100 m×100 m的二维环境,设置不同场景环境地图共八幅作为测试环境地图,八幅环境地图起始点坐标以及栅栏线数量如表1所示。
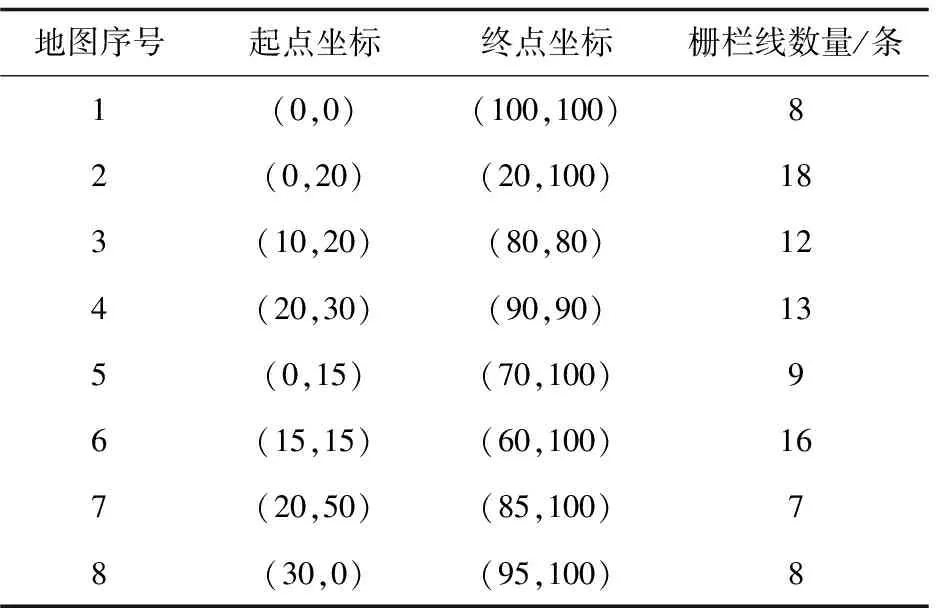
表1 机器人场景地图设置
统计采用文中方法对地图1实施机器人路径规划的进化曲线,为直观验证文中方法的规划性能,选取人工势场方法(参考文献[4])以及萤火虫方法(参考文献[5])作为对比方法,进化曲线对比结果如图1所示。
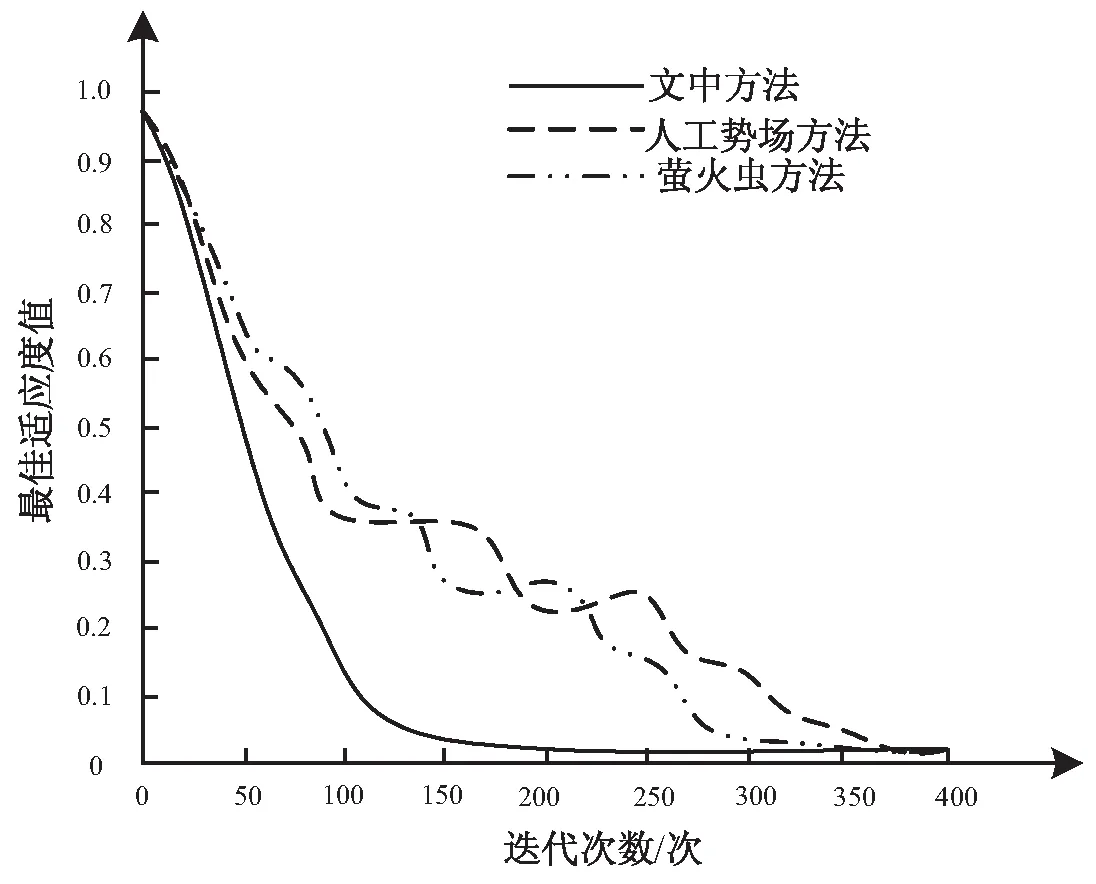
图1 进化曲线对比
从图1可以看出,采用文中方法规划机器人路径,仅需150次左右即可实现稳定收敛;采用萤火虫方法规划机器人路径,需300次左右才可实现稳定收敛;采用人工势场方法规划机器人路径,需350次左右才可实现稳定收敛。文中方法收敛速度明显高于另两种方法,说明文中方法可快速获取全局最优解,规划路径所需消耗时间低于另两种方法。
采用三种方法对地图1实施机器人路径规划的规划结果如图2所示。
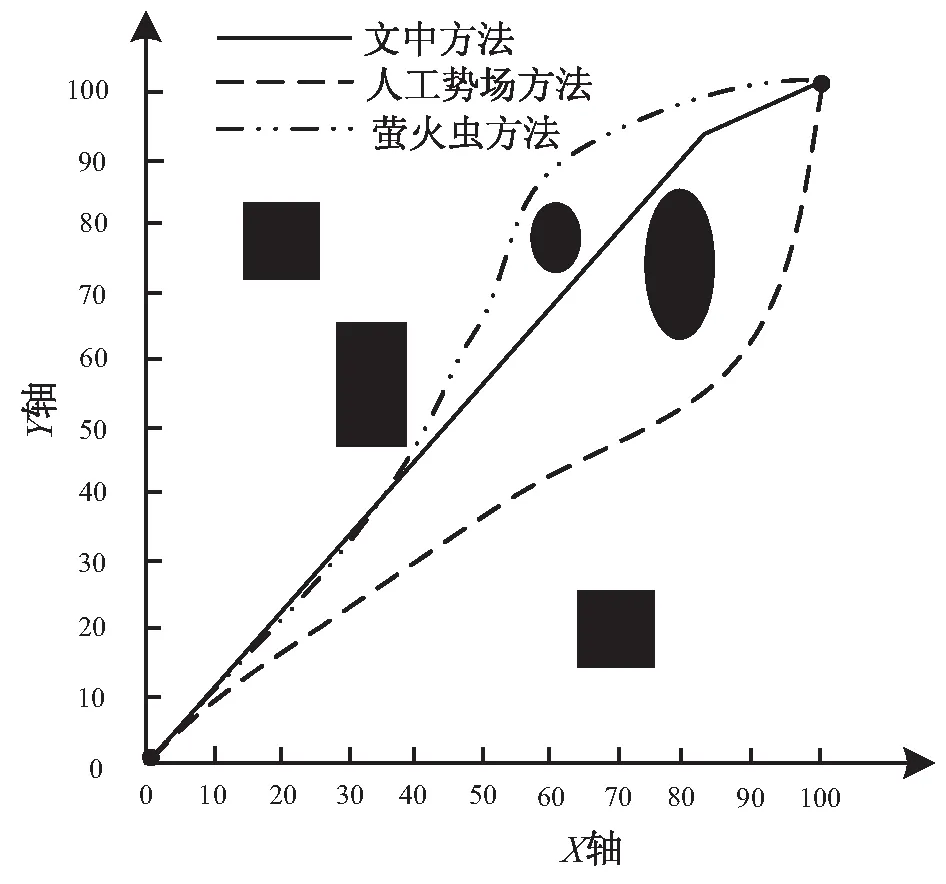
图2 地图1路径规划结果对比
从图2可以看出,采用三种方法均可基于地图1的环境地图实现机器人行驶路径有效规划。
为进一步验证文中方法对机器人路径的规划性能,统计采用三种方法对8幅地图实施机器人路径规划,重复10次迭代的最长路径、最短路径以及平均路径,对比结果如表2所示。

表2 机器人路径长度规划结果
从表2可以看出,采用文中方法对8幅地图实施机器人路径规划,规划结果的最长路径、最短路径与平均路径均明显低于另两种方法,说明文中方法规划机器人行驶路径时,可有效获取机器人行驶的最短路径,可满足路径总长度最短的目标。相比于人工势场方法以及萤火虫方法,文中方法所规划路径明显优于另两种方法,可有效获取机器人最优行驶路径,验证了文中方法的收敛精度较高。采用文中方法规划机器人行驶路径时,可有效解决复杂路径规划问题,验证了文中方法的机器人路径规划的有效性。
统计采用三种方法对8幅地图实施机器人路径规划,所获取规划路径的安全度,对比结果如图3所示。
从图3可以看出,采用文中方法规划机器人行驶路径,规划不同地图的路径安全度均明显高于另两种方法。采用文中方法规划机器人行驶路径可满足路径安全度最高的目标。文中方法可有效解决多目标优化问题,路径规划性能较高,同时满足路径总长度最短以及路径安全度最高的规划目标。
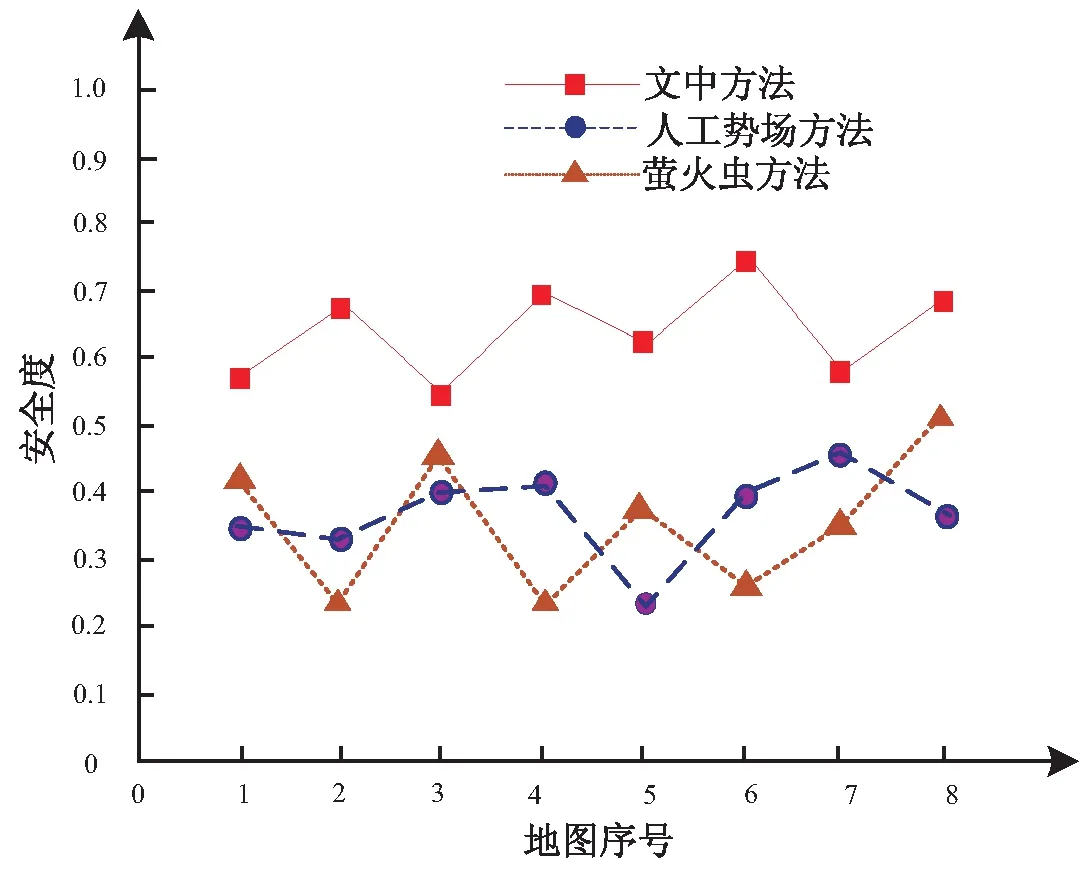
图3 路径规划安全度对比
统计采用文中方法规划机器人行驶路径的规划时间,统计结果如表3所示。

表3 不同地图规划时间对比
从表3可以看出,采用文中方法规划机器人行驶路径的规划时间明显低于另两种方法,采用文中方法规划8幅地图中机器人行驶路径的规划时间均低于400 ms,说明文中方法不仅可以有效规划机器人行驶路径,且规划时间短,可满足机器人路径规划实时性需求。文中方法在地图存在障碍物情况时仍具有较高的规划性能,可获取满足优化目标的最优路径,验证了文中方法具有较高的路径规划有效性以及可行性。
3 结束语
通过改进人工鱼群法实现机器人路径规划,利用自适应视觉范围以及拥挤度因子,提升改进人工鱼群法的全局搜索能力。将人工鱼群法中的鱼群历史最优位置利用公示牌记录,避免由于人工鱼群法中鱼群游动造成最优点有所改变,无法稳定问题。通过实验验证该方法可在较少迭代次数快速获取机器人全局最优路径。改进人工鱼群法可提升机器人路径规划实时性,为机器人路径规划提供科学、合理的理论依据。
