基于克里金算法的井田煤层三维建模方法研究

张小艳，王萌娟

(西安科技大学 计算机科学与技术学院，陕西 西安 710600)

0 引 言

近年来随着计算机科学技术与工业生产传统技术的快速融合与发展，数字化矿山已经成为了矿产行业的热点问题[1]。在建立煤层三维模型时，常用到的建模软件有Surpac Vision[2]、Google Ocean[3]、GOCAD[4]、3DMine矿业工程软件[5]、ArcGIS软件[6]、MICROMINE[7]、CATIA[8]、龙软[9]等，但采用这些软件所构建的三维模型很难进行跨平台使用， 同时也无法与煤矿企业现有的一些Web管理系统进行较好的兼并，不利于企业对信息的统一管理；同时，建模中常用的方法是单一空间插值算法或曲面拟合算法，不能很好地解决复杂的地质构造，构造的三维模型不太符合实际的煤层分布情况及空间关系[10]。因此，需要建立一个实现无插件、可移植、跨平台、准确度高、支持多浏览器运行的三维可视化模型。

在实际生产过程中，钻孔点不是按照规则化的网格进行获取的，而是空间中的随机离散点，钻孔数据没法做到规则化网格布点，也无需做如此大规模的浪费[11]，同时井田范围大、钻孔数据较少。为了构建一个能够精确地表征煤层分布情况的三维模型，该文首先采用改进的支持向量回归算法(SVR)优化克里金插值算法(Kriging)；然后，建立基于改进SVR的克里金高程估算模型，根据钻孔数据和煤层高程信息构建估算模型，对未知点的高程进行了估算，增加实现三维建模的数据点；最后，采用three.js技术和三角剖分算法[12]实现煤层三维模型，其能够较为精确地展示出煤层分布范围以及井田煤层空间关系。

1 理论基础

1.1 克里金插值算法

克里金算法是地质统计学中的一种空间插值技术，广泛用于各类观测的空间插值，地面风场、降雨、土壤、环境污染等领域。克里金插值法是根据采样点与估算点之间的位置关系与关联程度，由已知点的数据加权求和来估计未知点的值。它是一种具有无偏、线性特征的最优统计方法[13]。设x1,x2,…,xn为区域内的n个采样点，z(x1),z(x2),…,z(xn)为对应采样点的观测值。区域化变量在x处的估算值z*(x)表示为：

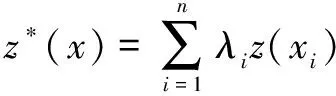
(1)

其中，λi(i=1,2,…,n)为权重系数，并且各权重系数的取值需满足两个条件：无偏性和最优性。权重系数λi的求解有两个步骤：首先，求得空间区域化变量对应的变差函数；其次，再进行插值[14]。

变差函数是用来表示区域化变量的空间结构特征，是克里金插值的基础。在求解变差函数模型中要求得三个参数：变程、块金值和偏基台值，这些参数反映了空间变化特征。在得到实验变差函数曲线之后，根据曲线的趋势去选择合适的理论变差函数模型，常见的三种理论变差函数模型有：球状模型、指数模型、高斯模型。

1.2 支持向量回归模型

在回归模型中，给定一组数据{(x1,y1),(x2,y2),…,(xm,ym)}，其中，xi∈Rd，yi∈R，希望学习到一个模型f(x)=ωTx+b，使得f(x)与y尽可能接近。支持向量机假设能容忍f(x)与y之间最多有ε的偏差，即仅当|f(x)-y|>ε时，才会计算损失[15]。SVR可以将模型转化为：

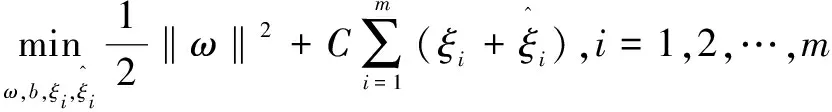
(2)

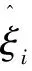
SVM算法在处理小样本、非线性和高维数等问题时有着许多独特优势，当模型为非线性回归时，SVR引入核函数，构造映射函数φ(x)将样本从原始空间映射到合适的可线性回归的特征空间中，从而使其线性回归。

1.3 可修改变异方向的差分进化算法

差分进化算法首先对种群进行初始化，然后通过对种群中所有个体进行变异、交叉操作，产生中间个体，将中间个体与当前种群中对应个体进行比较，选择出适应值较好的个体作为下一代的新个体。随着种群的进化，保留“基因”优秀的个体，确保最优个体逐步收敛至全局最优解[16]。为了提高差分进化算法的搜索效率，选用一种可以在变异过程中修正变异方向的自适应差分进化算法(UMDE)[17]，其中自适应的缩放因子定义为：

(3)

其中，fi(pre)是指当前个体的上一代个体的适应值，fmin(pre)是与上一代最优个体的适应值，fi(cur)为当代个体的适应值。如果在第一次变异之后，发现有个体适应值不如上一代个体适应值，则说明此次变异偏移了最优个体适应值的逼近方向，此时就需要适当调整缩放因子F，使其在下一次进化过程中向全局最优个体适应值的方向发展[17]。

2 UMDE-SVR-Kriging高程估算模型

地质统计学中的克里金插值算法已被应用在高程估算中，多位学者也证明了该算法有着较好的估算精度。因此，选择克里金插值算法对煤层高程进行估算。在克里金插值算法中，变差函数的求解是克里金插值算法的核心[18]。为了提高克里金算法的估算精度，该文采用UMDE优化后的SVR拟合克里金的实验变差函数。首先根据已有的钻孔坐标信息进行计算，得到实验变差函数值，并求得步长进行分组，然后求解SVR最优参数组，进而对变差函数进行拟合。采用改进的支持向量回归算法拟合变差函数能够克服常规克里金对变差函数选择的依赖性、局限性，以及变差函数选择的主观性和人为性，进而提高克里金插值算法的估算精度。

2.1 基于差分进化算法优化的支持向量回归

在SVR的参数求解中，运用UMDE算法优化支持向量回归，随着进化代数不断的增加，通过变异、交叉、选择操作，取得SVR最优的参数对(ε,C,γ)，求解步骤如下：

Step1：确定所求参数(ε,C,γ)；

Step2：初始化种群，其中差分进化算法的种群数量为100，缩放因子为0.6，交叉概率为0.65，遗传代数为500；

Step3：计算种群中各个个体的适应度值；

Step4：条件判断，若达到最大进化代数，则停止，输出最优结果，否则继续执行下一步；

Step5：执行差分进化操作，进行交叉、变异以及选择操作，生成新一代；

Step6：进化代数加一，然后跳转到第4步。

通过以上步骤的运算，便可求解到SVR最优参数对(ε,C,γ)。采用UMDE优化SVR，通过种群的不断迭代，UMDE在交叉、变异、选择操作后，求解出SVR的最优参数组，提高了SVR的拟合精度，为构建基于SVR的克里金高程估算模型奠定了基础。

2.2 UMDE-SVR-Kriging高程估算模型建立流程

基于UMDE-SVR的克里金算法高程估算模型建立流程如下：

Step1：准备构建模型所需的钻孔数据、煤层高程数据、煤层厚度数据，并对数据进行正态分布检验，若不满足，对数据进行处理，使其正态分布；

Step2：将观测点进行两两配对，计算每对数据点之间的距离以及半方差值。例如有采样点(x1,x2,x3)，将数据点进行两两配对之后有数据点对(x1,x2)，(x1,x3)，(x2,x3)，计算每对数据点之间的距离和半方差值，点对之间距离时选择欧氏距离，如公式(4)所示，半方差值的公式为公式(5)；

(4)

(5)

Step3：利用采样点数据计算变差函数值可以得到实验变差函数云图，它以离散且不规则的形式存在，需要对其进行处理才能使用。因此需要对步骤2中求得的距离进行分组，并计算组内变差函数值的平均值作为该组的值，在分组时选择平均最近距离作为步长对其进行分组；

Step4：拟合实验变差函数，采用2.1小节中的UMDE-SVR算法拟合变差函数，求得最优的SVR参数对，最终确定最优理论变差函数；

Step5：根据求得的变差函数模型构建的高程估算模型，对未知点的高程值进行插值估算。

变差函数反映的是区域化变量的空间变化结构，是克里金插值算法的基础。大多数变差函数模型的求解，往往是依据计算得到的变差函数值所绘制的实验变差函数云图的图形曲线，选择合适的理论变差函数模型，因此，变差函数模型的选择较为局限，影响了模型的精度。采用UMDE-SVR来对克里金插值算法的变差函数进行拟合，构建符合变差函数的最优理论变差函数模型，避免了选择常规的几种模型的局限性，以及模型选择的主观性，从而使得高程估算模型有着较高的估算精度。

3 实验与结果分析

3.1 实验验证与分析

本次实验数据来源为某煤矿的真实数据，包括钻孔数据、煤层数据以及各煤层的煤质信息，有705个钻孔数据，9层煤层数据，其中有8层煤为可采煤层。根据实验要求对数据进行处理，从钻孔数据表中提取钻孔编号、钻孔坐标X和Y；在煤层信息表中，将各个煤层的煤层信息进行整理，其中包括煤层编号、钻孔编号、煤层底板高程、煤层厚度；将各个煤层的钻孔编号与钻孔信息表中的钻孔编号对应，将煤层编号、钻孔编号、钻孔坐标X和Y、煤层底板标高、煤层厚度进行整合，构建了各个煤层信息表。本次实验采用的数据主要为钻孔坐标、煤层底板标高以及煤层厚度。

(1)实验环境。

本次实验的实验环境如表1所示。

表1 实验环境

(2)检验数据分布。

根据正态QQ图可以判断插值对象是否服从正态分布。在正态QQ图中，如果数据点围绕着一条直线上下波动，则服从正态分布。对于不服从正态分布的数据，可以对其采用对数变换、幂变换等方法，使其满足正态分布。

在ArcGIS软件中对该5-2煤层的高程数据进行空间数据探索性分析，得出其分布的正态QQ图(见图1)。

在图1中，可以看到数据点近似分布为一条直线，该煤层的高程值十分接近标准正态分布，满足插值对象为正态分布的前提条件。

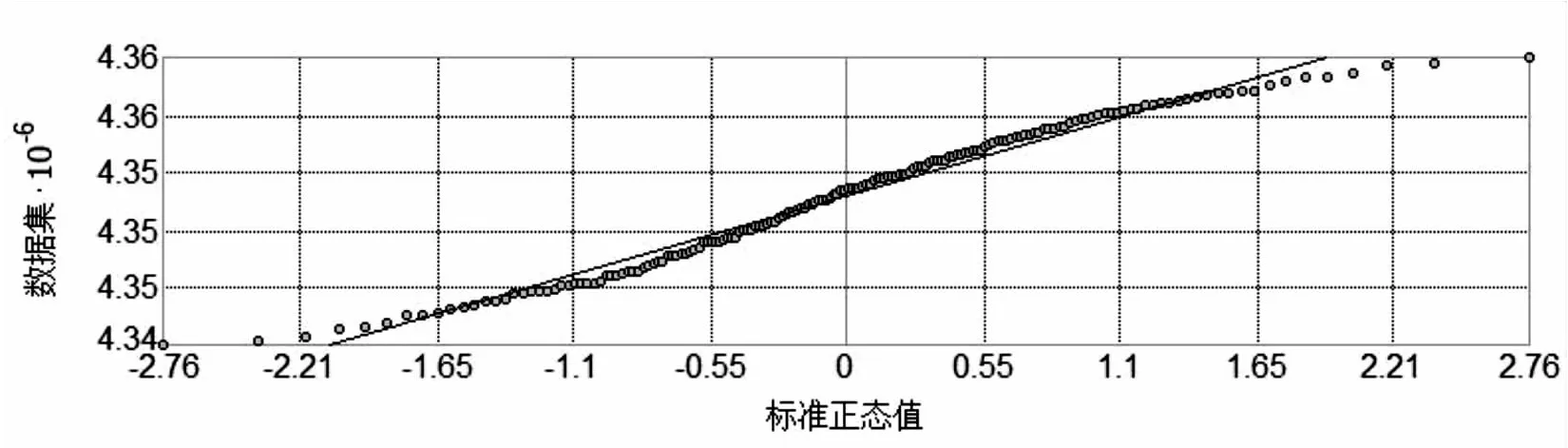
图1 5-2煤层高程值正态QQ图

(3)实验过程。

第一步：计算实验变差函数值，绘制变差函数云图。

当对5-2煤的钻孔数据(172组)进行两两配对计算其距离以及半方差值后，会得到如图2所示的实验变差函数云图，x轴表示点对之间的距离，也称滞后距，y轴表示其相应的实验变差函数值，即计算得到的半方差值。

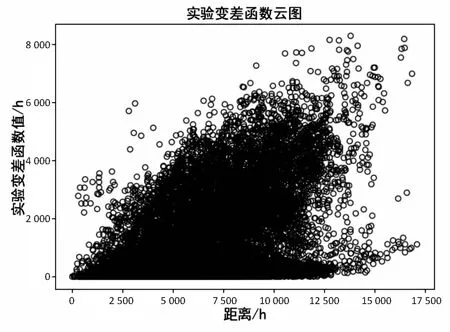
图2 5-2煤实验变差函数云图

第二步：计算步长并进行分组。

在图2中，可以看到图中的数据点分布散乱，很难对其进行求解，因此在实际的应用中，需要对其按照步长进行分组，求得组内平均值并绘制变差函数云图，然后再进行求解。本次实验中采用平均最邻近距离作为分组步长，根据上一步计算得到的点与点之间的距离，计算得到平均最近邻距离值为640.720 37，在具体实验中对其进行取整，即取分组步长为640 m，对图2中的点对进行分组，数据点可分为27组，得到分组后的实验变差函数云图，如图3所示。

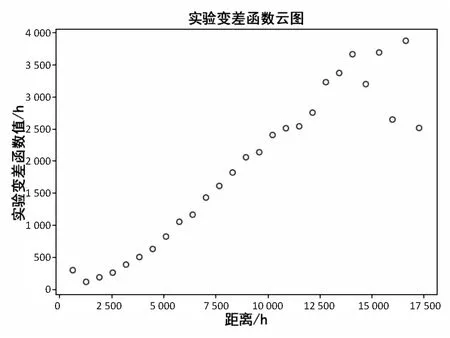
图3 5-2煤分组后实验变差函数云图

第三步：利用UMDE优化支持向量回归，得到支持向量参数。

根据分组后得到的实验变差函数值、距离值，采用自适应差分进化算法优化SVR，得到SVR最优参数组，其中差分进化算法的种群数量为100，缩放因子为0.6，交叉概率为0.65，遗传代数为500。

第四步：采用UMDE-SVR拟合变差函数并估算高程值。

根据第三步得到SVR最优参数组(ε,C,γ)为(1.81e-12，100.0，0.62)，拟合变差函数，构建高程估算模型。设搜索点数为30，对样本点高程进行插值估算。

为了合理评价UMDE-SVR-Kriging模型的估算效果，选用5-2、1-2煤层数据，与UMDE-Kriging的指数、高斯、球状模型，基于改进粒子群的SVR(Ipso-SVR)克里金法，以及基于留一法的SVR(Loo-SVR)的克里金法，在同一数据集上进行实验，通过均方误差(MAE)与均方根误差(RMSE)两个指标来评价模型的估算效果，证明UMDE-SVR-Kriging模型的高估算精度，结果如表2和表3所示。

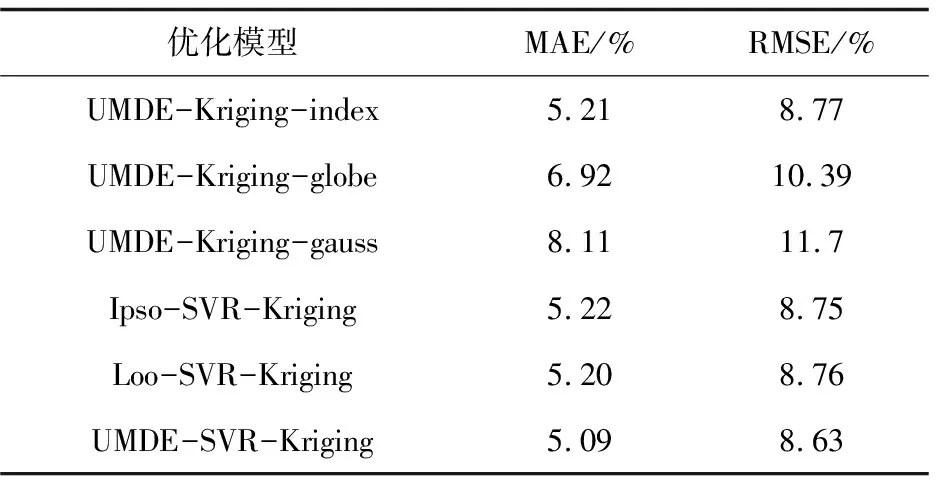
表2 5-2煤不同高程估算模型实验结果比较

表3 1-2煤不同高程估算模型实验结果比较

根据表2和表3中的实验结果，可以明显看到，相较于UMDE-Kriging算法的指数模型、高斯模型、球状模型，Ipso-SVR-Kriging以及Loo-SVR-Kriging，UMDE-SVR-Kriging的MAE和RMSE值较小，说明该模型估算的高程值相较于其他模型更为精准，证明了采用基于差分进化算法优化的SVR的克里金高程估算模型在煤层高程估算方面有着较高的估算精度，以及模型在井田煤层高程估算的可行性。

3.2 三维可视化

由于现有井田钻孔数据较少，画图无法真实反映煤层的分布情况，因此该文采用改进的SVR的克里金高程估算模型对未知点的高程值进行估算，增加三维建模数据，从而使得绘制出的煤层三维图更符合现实情况，并在3.1小节中通过实验证明了UMDE-SVR-Kriging高程估算模型的较高估算精度以及可行性。

因为煤层有着一定的厚度，煤层上下有着不同的变化规律，现有数据为钻孔坐标、煤层底板高度及煤层厚度，根据底板高度和煤层厚度，计算得到某个钻孔坐标煤层上的高度，之后分别对煤层上下的高程分别建立估算模型，实现对未知点的煤层上下高度的估算。

采用2.2小节中介绍的UMDE-SVR-Kriging模型分别建立煤层上下的高程值的估算模型，实现对未知点的高程值的估算。在数据点选择中，以钻孔坐标X、Y的最大值和最小值为最大范围，随机选取一定个数的未知点坐标，利用构建的煤层上下高程值的估算模型对同一坐标点煤层上下高程值进行插值估算，求得未知点煤层上下的高程值。根据估算得到某点煤层上下的高程值可以得到该点煤层厚度，已知每层煤层厚度范围，通过对估算得到的煤层厚度进行筛选，得到有效的估算点进行绘图。

为了建立无插件、可移植、跨平台、准确度高、支持多浏览器运行的煤层三维可视化系统，以Visual Studio为开发工具，采用vue框架等构建了井田煤层三维可视化系统，three.js三维引擎和三角剖分算法，以及原始数据如表4所示，UMDE-SVR-Kriging高程估算模型估算得到的5-2煤的高程数据如表5所示，实现web端的5-2煤的三维模型，如图4所示。

表4 5-2煤原始部分数据

表5 5-2煤估算得到的部分数据

图4 5-2煤层图

根据图4，可以看出5-2煤层的大致范围和分布情况，同时可对图形进行旋转，查看不同方向的煤层情况。

已知某井田内可采煤层共有8层，为1-2上、1-2、2-2、3-1、4-2、4-3、4-4、5-2煤层。分别根据各个煤层的钻孔坐标及高程数据，基于改进的SVR的克里金高程估算模型建立不同的估算模型并进行估算。根据各煤层估算得到的有效数据以及原始数据，采用Three.js三维引擎和三角剖分算法实现该井田8层煤的三维可视化模型，如图5所示，从上往下分别是1-2上、1-2、2-2、3-1、4-2、4-3、4-4、5-2煤层。

图5 某井田煤层图

由图5可以看出该井田的8层煤的分布和范围情况以及空间特性，并且在该模型中，可以随机选择煤层号，展示该煤层的具体情况。

4 结束语

由于在实际生产过程中，井田原始钻孔数据稀疏，由此数据绘制的煤层三维图无法真实地展示出煤层分布情况。该文构建了基于克里金插值算法的高程估算模型，对未知点高程值进行估算，增加绘图数据点。为了提高克里金的估算精度，采用改进的支持向量回归对克里金进行了优化，构建了基于UMDE-SVR优化的克里金高程估算模型，采用某煤矿实际数据，将该模型与差分进化算法优化的克里金的指数、球状、高斯模型，基于改进粒子群的SVR克里金法，以及基于留一法的SVR的克里金法的估算精度进行了对比，分别对某矿5-2、1-2煤层的高程值进行估算。实验结果表明，UMDE-SVR-Kriging模型的MAE与RMSE值都较优，证明了该模型有着较高的估算精度，可为井田煤层三维模型的实现提供技术支持。通过UMDE-SVR-Kriging模型构建的某井田煤层的三维模型，能够更为真实地展现出该井田煤层的分布情况，并且可以与煤矿企业现有的Web管理系统进行良好的契合，对煤矿企业的生产起到了很好的指导作用。