基于变动饱和带的产汇流模型及其参数确定方法
2022-05-10李彬权梁忠民付宇鹏胡义明
李彬权,梁忠民,付宇鹏,王 军,胡义明
(1. 河海大学水文水资源学院,江苏 南京 210098;2. 河海大学水科学研究院,江苏 南京 211106;3. 水利部珠江水利委员会水文水资源局,广东 广州 510611)
在全球气候变化与高强度人类活动影响的大环境下,原本依据天然降雨径流关系的水文模型或预报模式已经无法满足当前复杂下垫面环境以及对预报精准度日益增长的需求[1- 3]。当前变化环境下洪水预报面临新的问题和挑战,主要表现在[4- 5]:① 气候变化导致降水特征发生变化,水循环加快,极端事件增加,沿海防洪能力下降;② 下垫面变化改变了流域产汇流规律,破坏资料系列的一致性,模型参数的代表性不复存在,特别是资料缺乏地区的洪水预报问题仍是重大难题。气候变化和人类活动破坏了水文系列的代表性,资料不能满足模型参数率定的要求[6]。因此,亟需创新模型的理论方法,以反映下垫面变化对产汇流过程的扰动;发展分布式水文模型的物理确定方法,以解决资料缺乏地区模型参数的确定难题。
1995年,Garrote和Bras[7]在Cabral下渗理论[8]基础上,通过研究湿润锋演进及相对不透水层(变动饱和带)产生与发展过程,建立土壤水分剖面变化的数学表达方程,提出了一种描述径流发生位置及多源径流成分的新型产流模式,并逐步发展成为完整的分布式水文模型RIBS(Real- Time Interactive Basin Simulator)[9]。这种新型产流模式有别于传统的蓄满- 超渗2种产流机制水平向或垂向组合方式,避免人为设定某种产流机制的主观性,更接近真实的产流过程,但仍难以突破当前分布式水文模型的最大应用瓶颈,即参数高度依赖率定,在资料缺乏地区应用精度受限[10- 11]。
本文综合RIBS模型中的变动饱和带产流模式和网格水滴汇流方法,构建基于单元网格剖分结构的分布式产汇流模型,分析模型参数敏感性,建立敏感性产流参数与地形参数、土壤类型数据之间的统计关系,结合野外坡面流观测试验确定汇流参数,在多个实际流域进行应用检验。
1 基于变动饱和带的产汇流模型构建
构建的模型中产流模块为RIBS模型中变动饱和带产流模式[9],汇流模块借鉴了文献[12]提出的“网格水滴”汇流计算思路,由此构建得到的产汇流模型结构如图1(a、b、c分别代表③ 、⑤ 、⑦ 单元内的河段)所示。本节简要介绍模型产汇流计算的主要过程,详细内容可参阅文献[7- 9,12]。
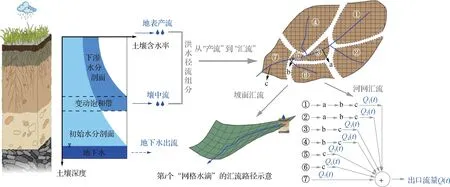
图1 基于变动饱和带的产汇流模型结构Fig.1 Framework of the rainfall- runoff model based on variable saturation zone concept
1.1 基于变动饱和带概念的产流模型介绍
1.1.1 产流模型基本假设
下渗模型包括非饱和下渗和饱和下渗2个阶段。由于饱和水力传导度随深度减小,随着下渗量的累积,土壤将有可能形成变动饱和带。忽略毛管力作用[13],则重力是非饱和下渗的主要作用力;同时在场次洪水模拟预报过程中假定地下水位恒定不变。以下垫面网格单元地表处为原点建立坐标系,与地面平行的方向为x方向(坡度下降方向为正),与地面垂直的方向为z方向(向下为正)。假定土壤饱和水力传导度(Ks)随深度呈指数衰减,即
Ksz=K0zexp(-fd)Ksx=K0xexp(-fd)
(1)
式中:d为土壤深度,mm;Ksz为z方向的土壤饱和水力传导度,mm/h;K0z为z方向的地表饱和水力传导度,mm/h;f为饱和水力传导度随深度衰减系数,取值为0~1 mm-1;Ksx和K0x分别为x方向的土壤饱和水力传导度和地表饱和水力传导度,mm/h。引入各向异性比率αr=K0x/K0z>1,描述z与x两方向上饱和水力传导度的关系[8]。
采用Brooks和Corey方法[14]计算z、x方向的非饱和土壤水力传导度分别为:
(2)
(3)
式中:Kz、Kx分别为z、x方向的非饱和土壤水力传导度;ε为土壤孔隙分布指数;λ为土壤孔隙分布指数;Se为关于土壤含水率(θ)的量纲一变量;θs为饱和土壤含水率,一般取值为0.3~0.6;θr为残余土壤含水率,一般取值为0.01~0.15。
1.1.2 恒定雨强的下渗模型
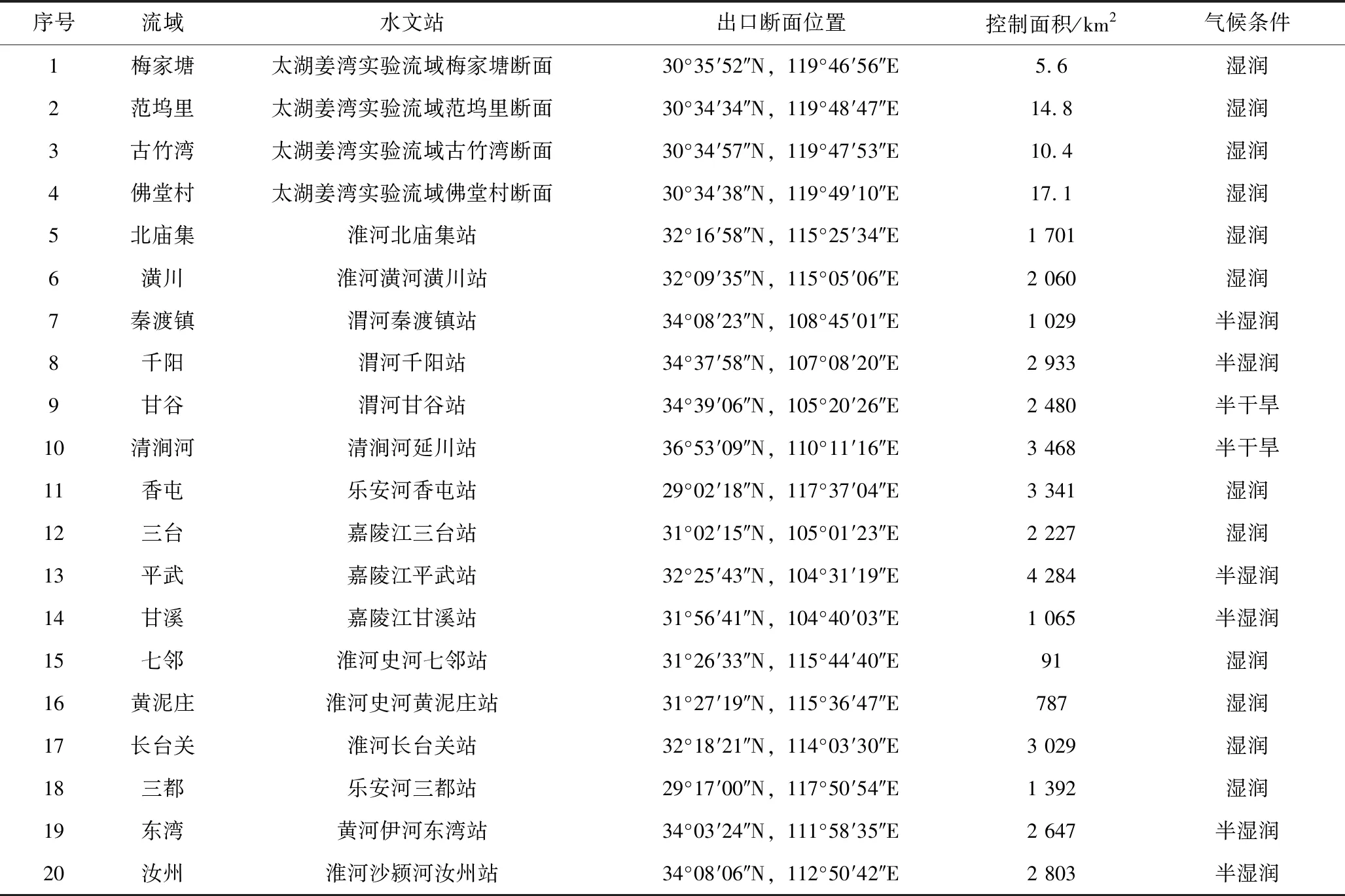
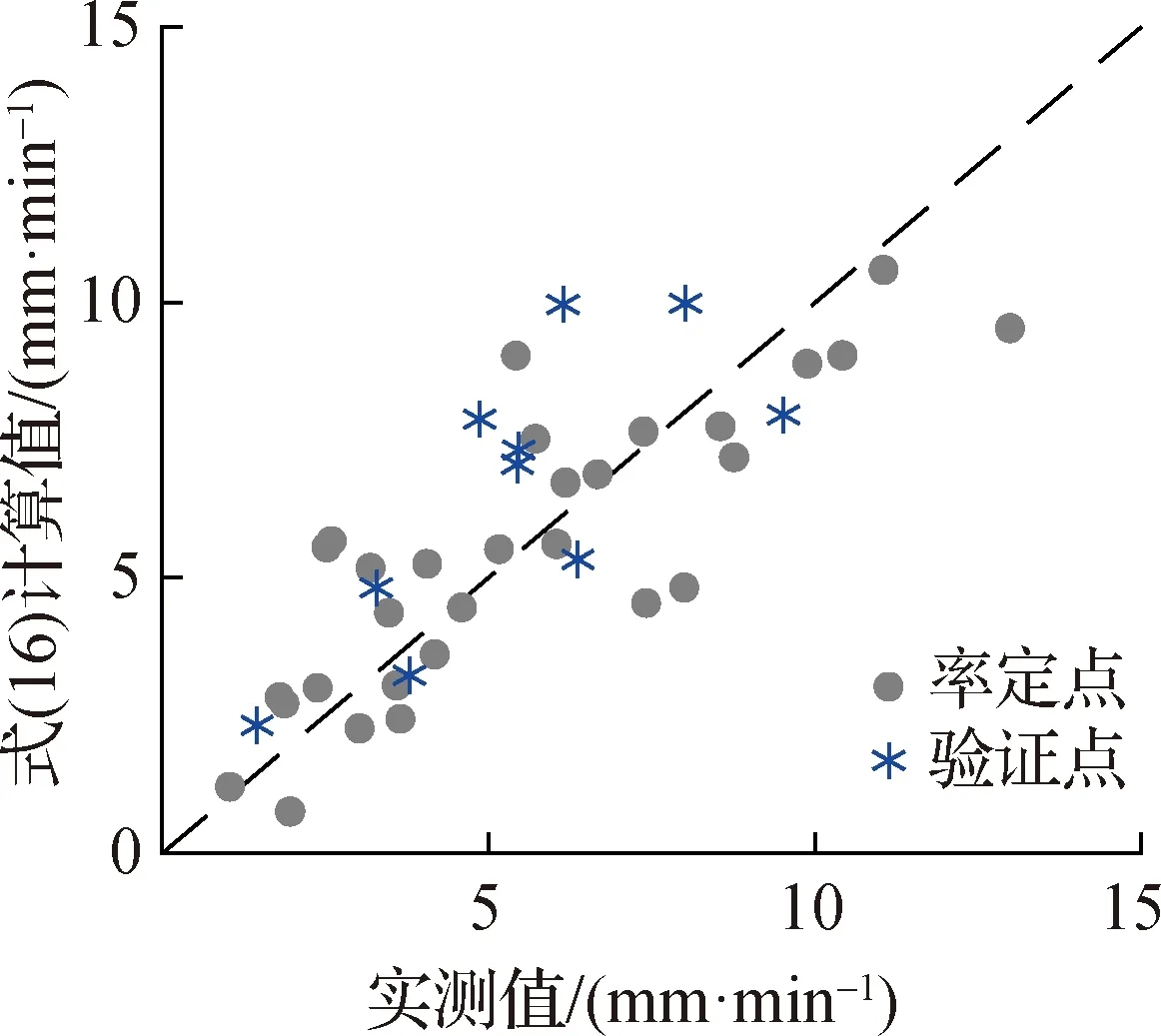
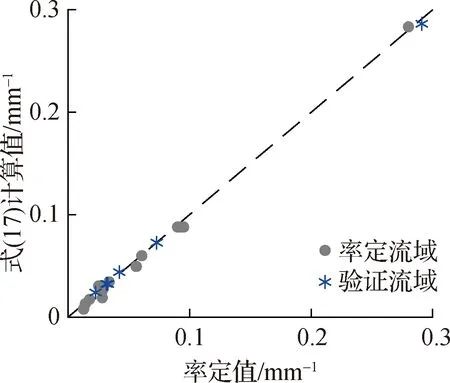
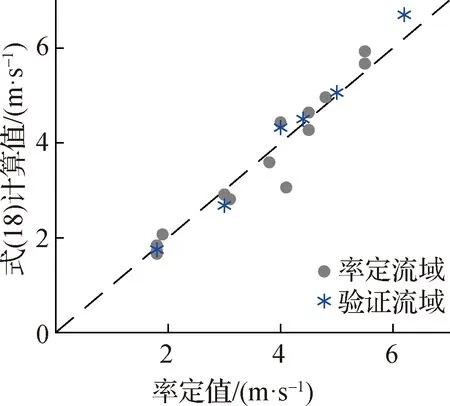
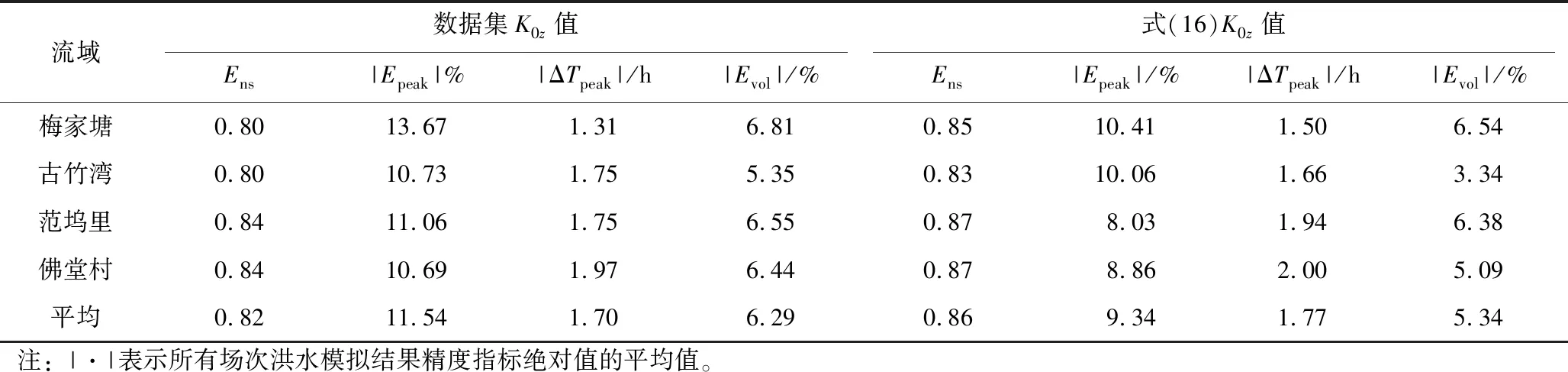
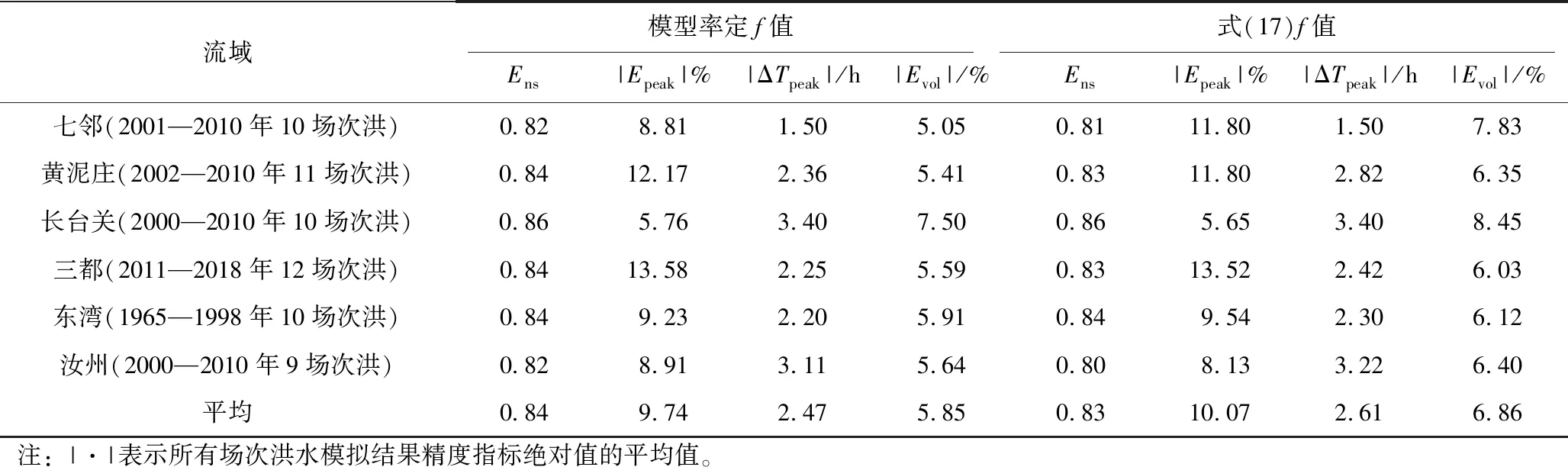
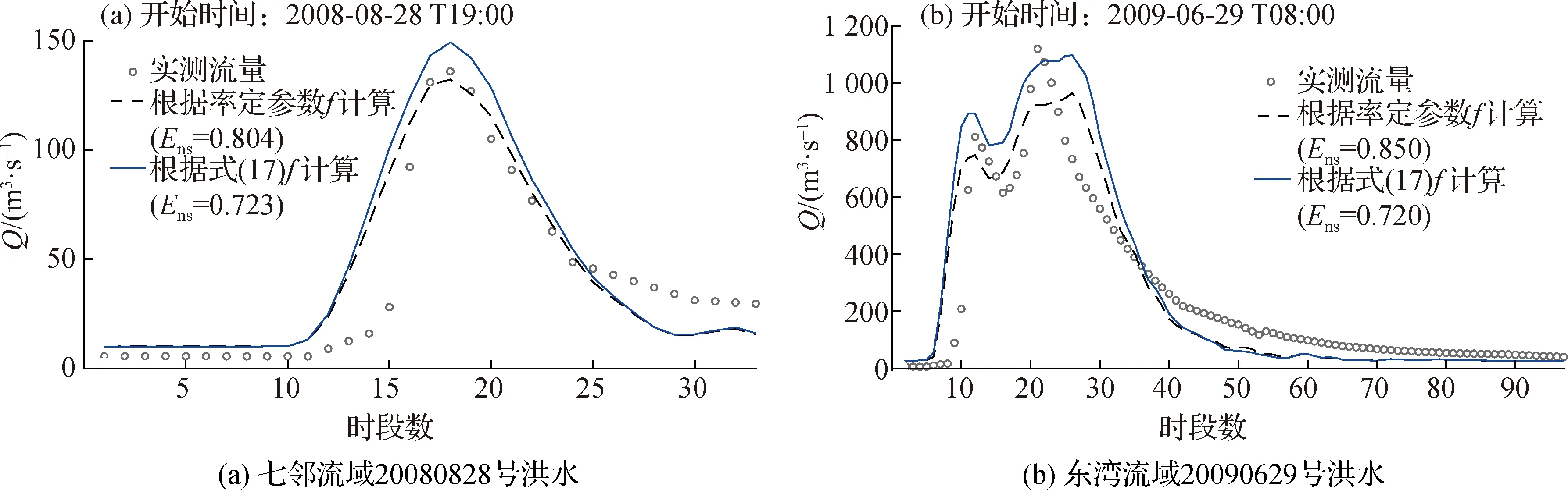
在恒定降雨强度条件下,土壤水分剖面通常会经历4个连续的状态过程(图2),湿润锋的位置深度记为NW,变动饱和带的上边界深度记为NU,地下水深度记为NG,4个状态下各深度之间关系为:① 非饱和状态NW≤NU 图2 土柱单元不同水分状态示意Fig.2 Schematic diagram of different moisture states of soil column unit 在变动饱和带尚未产生条件下,饱和水力传导度随深度递减,因此当恒定降雨强度I≤K0z时,一定存在一个深度Nb,使得该深度z方向上的饱和水力传导度与雨强相等,即Kz(θs,Nb)=I, 代入式(2) 得到[8]: (4) 在此深度之下,饱和水力传导度小于恒定雨强,湿润锋下降速率小于恒定雨强,因而水分在此深度以下开始逐渐积累,产生变动饱和带。在湿润锋到达Nb之前,湿润锋与土柱表面之间处于非饱和状态。定义一个比较小的恒定雨量为I0(取I0=0.1 mm/h),在持续时间较长的恒定雨强I>I0条件下,土壤水分剖面分成受I影响和湿润锋NW之下仍只受I0影响的2个不连续区域。 在I>K0z和NW>Nb2种条件下,湿润锋以上的土壤会处于饱和状态。定义Keq为饱和区域内饱和水力传导度的调和平均值: (5) NW和NU的计算公式为: (6) (7) 式中:α为网格单元地表与水平面的夹角;θI0,NW和θI,NU分别为受I0影响的NW处土壤含水率和受I影响的NU处土壤含水率。 在I (8) 1.1.3 变化雨强的下渗模型 为简化变化雨强条件下土壤水分剖面计算的难度,模型假定[7]:在变化雨强下只有第1个湿润锋向土壤深处运动,此后下渗水量均补充第1个湿润锋,直到土壤达到完全饱和状态。为此,引入等效降雨强度(Ie),该值将使得湿润锋以上非饱和区域的土壤含水量与变化降雨强度条件下实际土壤含水量相等。 应用迭代法求解土壤水分剖面方程可得到Ie的数值[7]。产生变动饱和带后,湿润锋控制方程2个变量NW、NU可由下式确定: (9) (10) 式中:θIe,NU为受Ie影响的NU处土壤含水率。 1.1.4 产流计算公式 在时间步长Δt内下垫面网格的地表产流量为 (11) 式中:Rf为地表产流量,mm。 相应的壤中流产流量为 (12) 式中:Rint为壤中流产流量,mm。 因此,在假定地下水位不变条件下产流总量为地表产流量与壤中流产流量之和。 所谓“网格水滴”,即将流域上降雨后有产流量的网格视作水滴,在重力驱动和阻力影响下沿地面坡度方向运动,每个水滴将在何时到达流域出口断面取决于路径长度和在路径轨迹上运动速度[12]。由于坡面与河网汇流的水力条件有所差别,坡面汇流和河网汇流采用不同的流速公式。 1.2.1 坡面汇流 根据流域DEM得到地形地貌信息,利用D8法确定流向和汇流路径长度。坡面流速主要受地形坡度、土地利用、地表糙率等因素影响,采用美国水土保持局提出的坡面流速公式为 (13) 式中:S为坡度;μ为坡度幂指数;Kv为坡面流速系数,m/s;ns为地表糙率,取值为0~1;m为糙率幂指数,一般取值为0.5~1.0。 1.2.2 河网汇流 对于“网格水滴”汇流路径上的河道网格而言,采用曼宁公式计算水滴的流速,公式为 (14) 式中:Cv为河网流速系数,m/s;nc为河道糙率;Rc为河道水力半径。 根据式(13)和式(14)确定的水滴流速,结合汇流路径长度即可得到水滴汇流时间为 (15) 式中:ti为第i个网格水滴的汇流时间,s;di为第i个网格水滴的汇流路径长度,m;Vi(x)为第i个网格水滴的流速。 选取20个流域的历史场次洪水资料用于模型参数确定和应用检验,各流域的出口断面水文站地理位置和流域控制面积见表1。其中,前4个流域属于太湖东苕溪支流余英溪姜湾水文站以上流域(姜湾流域)的子流域,是以和睦桥实验站[15]为基础发展而成的野外山坡实验流域。姜湾流域4个子流域的DEM空间分辨率为100 m,模型模拟时间步长为30 min;其他流域的DEM空间分辨率为1 km,模型模拟时间步长为1 h。 表1 选用的20个流域地理位置和控制面积 采用普适似然不确定性估计方法(GLUE)[16]分析6个产流参数的敏感性,先验分布为均匀分布,似然函数为确定性系数(Ens),其阈值取0.5。各流域的敏感性分析结果大致相同,参数K0z和f的较小改变均会导致Ens值的较大改变,θs、θr、ε和αr4个参数取值变化对模型精度影响不大。因此,参数K0z和f为敏感性参数,其他产流参数不敏感。 3.2.1 地表饱和水力传导度 选择姜湾流域开展野外双环入渗观测试验,建立地表饱和水力传导度实测值与地形参数的统计关系。在实验流域河谷内选择40个试验点,每个试验点开展5次以上平行的双环入渗观测试验,分析得到平均稳定下渗率,代表试验点所在下垫面网格(100 m×100 m)地表饱和水力传导度的平均值。 利用GIS软件提取得到姜湾流域下垫面网格的3类10个地形参数:① 一阶地形因子:坡度(Tslo)、坡向(Tasp);② 二阶地形因子:剖面曲率(Tpro)、平面曲率(Tpla)、坡度变率(TSOS)、坡向变率(TSOA);③ 复合地形因子:地表切割深度(Tcde)、粗糙度(Trou)、地形起伏度(Ttop)、高程变异系数(Tvar)。利用入渗试验的前30组试验资料建立地表饱和水力传导度与10个地形因子之间的统计关系,并利用后10组试验资料进行验证。建立的统计关系式见式(16),试验实测值与公式计算值对比结果如图3所示,式(16)的决定系数为R2=0.76,表明其具有较高的参数估计精度。 K0z=11 692.152+0.054Tasp-272.04Tpla-640.902Tpro+84.252Tslo-19.338Tcde- (16) 3.2.2 饱和水力传导度随深度衰减系数 参数f与土壤粒径随深度的变化有关,因此可通过建立f与不同深度土壤粒径的关系来确定该参数值。由于数据分辨率限制,难以采用试验测定方式获取下垫面网格参数f的真实值。本文通过模型率定获取流域空间平均的参数f值,建立率定的参数f值与不同深度土壤类型的统计关系式。土壤资料来源于中国科学院资源环境科学数据中心,包括表层(0~30 cm)和深层(30~100 cm)的砂土、粉砂土、黏土3种土壤类型数据。选用表1中前14个流域场次洪水资料率定参数f值,建立与不同深度土壤类型的统计关系式见式(17),决定系数为R2=0.995;选用表1中后6个流域资料进行验证,对比结果如图4所示。 f=-0.008Tsand-0.006 8Tsilt+0.000 01Tclay+0.006 3Ssand+0.004 1Ssilt+0.009Sclay (17) 式中:Tsand为表层砂土含量, %;Tsilt为表层粉砂土含量, %;Tclay为表层黏土含量, %;Ssand为深层砂土含量, %;Ssilt为深层粉砂土含量, %;Sclay为深层黏土含量, %。 验证流域的式(17)计算值与参数f率定值非常接近,相对误差为-1.6%~6.2%,平均相对误差绝对值为2.8%,表明该关系式较合理,结果具有较高精度。 3.2.3 非敏感性产流参数 非敏感性产流参数包括θs、ε、θr和αr。其中,θs和ε来源于根据遥感资料反演的全球土壤水力参数数据集[17](空间分辨率为30″),θr可基于表层土壤粒径分布数据利用经验公式[17]估算得到。根据已有研究经验[7- 9],参数αr可取10。 3.3.1 坡面汇流参数 坡面汇流参数包括Kv、ns、nc、m和μ。其中,ns、nc根据土地利用类型和文献[18]中给出的糙率经验值来确定,其他3个参数根据姜湾野外实验流域的坡面流观测试验分析确定。选用姜湾流域和睦桥实验站5场降雨(20180724、20180726、20180803、20180813、20180816)7个山坡共35组坡面流速观测数据,根据式(13)建立方程组,求解得到Kv=0.009 9 m/s,m=1.089,μ=0.65。 3.3.2 河网汇流参数 河网汇流模块的唯一参数为Cv,在假定河道糙率固定条件下取决于Rc,而Rc与水面宽(河宽)有关。借鉴已有文献研究成果[19- 20],在资料缺失地区忽略河道糙率,仅考虑水力半径的影响,Cv的估算公式为 (18) 式中:B为流域出口处河宽,m;c1、c2、c3为需要确定的参数。 采用表1中1—14流域场次洪水资料率定式(18),后6个流域资料进行验证,对比结果如图5所示。流域出口断面河宽结合水文站基本情况、野外实测和卫星影像综合估算,率定得到参数值为c1=0.074 5、c2=466.930 5、c3=0.362 2,关系式的决定系数为R2=0.925。验证流域的式(18)计算值与Cv率定值非常接近,相对误差均小于12%。 图3 K0z估算公式在姜湾实验流域率定与验证结果Fig.3 Calibration and validation of the estimate formula of K0z in the Jiangwan experimental watershed 图4 饱和水力传导度随f估算公式在20个流域的率定与验证结果Fig.4 Calibration and validation of the estimate formula of coefficient of attenuation of f in 20 basins 图5 Cv估算公式在20个流域的率定与验证结果Fig.5 Calibration and validation of the estimate formula of Cv in 20 basins 从场次洪水过程模拟角度检验模型应用效果,包括2个敏感性产流参数(K0z、f)确定方法与模型率定参数结果的对比分析。① 地表饱和水力传导度确定方法验证:选择姜湾流域梅家塘、范坞里、古竹湾、佛堂村4个子流域2018年7月至2020年8月共16场较大洪水进行模拟(11场用于率定,5场用于验证)。② 饱和水力传导度随深度衰减系数确定方法验证:选择表1中后6个流域的历史场次洪水进行模拟。模型模拟效果采用Ens、洪峰相对误差(Epeak)、洪峰滞时(ΔTpeak)和洪量相对误差(Evol)4个指标进行评定。 对比分析姜湾流域2套场次洪水模拟结果,见表2:① 参数K0z根据式(16)确定;② 参数K0z来源于全球土壤水力参数数据集[17];其他参数采用统一的率定值。对比各断面场次洪水模拟结果发现,除洪峰滞时指标外,式(16)的模型结果比遥感数据集中K0z值的结果精度更高,表明本文提出的参数K0z确定方法较为合理。图6给出了佛堂村子流域的验证场次20190901号洪水过程模拟结果,模拟时段步长Δt=30 min。 表2 参数K0z确定方法在姜湾流域场次洪水模拟中验证结果 图6 佛堂村子流域20190901号洪水过程模拟结果Fig.6 Simulated hydrographs for the flood #20190901 of the Fotangcun sub- basin 对比七邻等6个流域2套场次洪水模拟结果,见表3:① 参数f根据式(17)确定,其他参数通过率定获得;② 所有模型参数均通过率定获得。结果表明,6个流域的率定参数模拟结果均略优于式(17)的模型结果;总体上看,本文提出的参数f确定方法对应的场次洪水模拟的平均确定性系数为0.83、洪峰和洪量误差的平均绝对值分别为10.07%和6.86%、洪峰滞时误差的平均绝对值为2.61 h,满足精度要求。图7给出了七邻、东湾流域2场验证场次洪水的模拟结果,模拟时段步长Δt=1 h。 表3 参数f确定方法在6个流域场次洪水模拟中验证结果 图7 七邻流域和东湾流域洪水过程模拟结果Fig.7 Simulated the flood hydrographs the Qilin Basin and the Dongwan Basin 利用姜湾野外实验流域和16个实际流域的资料,建立地表饱和水力传导度和饱和水力传导度随深度衰减系数2个敏感性产流参数与下垫面特征数据的定量统计关系,并建立汇流参数的经验估计关系式。主要结论为: (1) 姜湾流域4个干流断面的实例应用表明,利用下垫面地形特征参数估算地表饱和水力传导度的方法在洪水模拟中精度较高,16场洪水的确定性系数、洪峰(洪量)误差和洪峰滞时误差均满足规范的精度要求;与使用遥感资料推求地表饱和水力传导度值得到的洪水模拟结果相比,除洪峰滞时误差略差外,其他3个精度指标均更优。 (2) 根据20个实际流域的资料对饱和水力传导度随深度衰减系数的估计关系式进行率定和验证,结果表明利用土壤质地数据估算深度衰减系数值的方法在场次洪水模拟中的精度指标均满足规范要求,但比单纯进行模型参数率定的结果略差。 (3) 提出的利用下垫面特征数据估算模型参数的方法在资料缺乏地区场次洪水模拟预报中具有适用性。
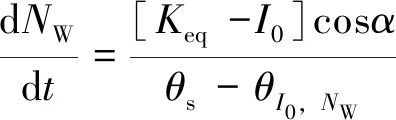
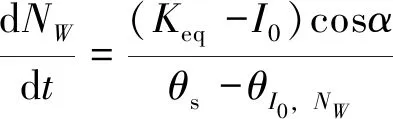
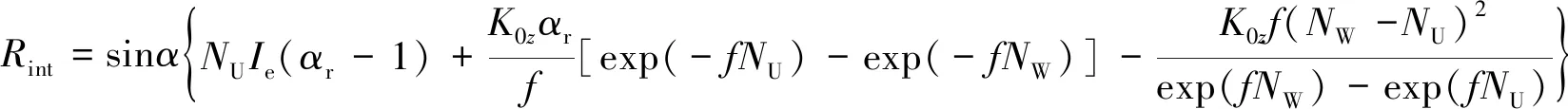
1.2 网格水滴汇流模型
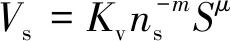
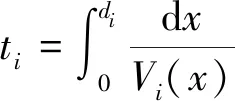
2 研究流域
3 模型参数的确定方法
3.1 参数敏感性分析
3.2 产流参数的确定
11 529.006Trou-3.354Ttop+135.792Tvar-34.326TSOS+0.894TSOA3.3 汇流参数的确定
4 模型的应用验证
4.1 参数K0z确定方法的验证

4.2 参数f确定方法的验证
5 结 论
