基于汇水区分级划分的城市洪涝模拟
2022-05-10王小杰夏军强董柏良侯精明李启杰
王小杰,夏军强,董柏良,侯精明,李启杰
(1. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2. 西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048 )
洪涝灾害是影响范围最广、死亡人数最多的自然灾害之一[1]。近几十年来,受全球气候变化和人类活动的双重影响,城市洪涝灾害问题日益严重[2]。据中国住房与城乡建设部统计,2008—2010年全国60%以上城市发生过不同程度的洪涝灾害,其中有近140个城市洪涝灾害超过3次以上[3]。据《中国水旱灾害公报》统计显示,2008—2018年全国年均有158座城市发生洪涝灾害,造成严重的经济损失和人员伤亡[4]。其中,2012年“7·21”北京特大暴雨洪涝灾害造成79人死亡和116.4亿元经济损失[2- 3];2016年7月武汉洪涝灾害造成全市12个区75.7万人受灾,直接经济损失22.7亿元[5];2021年“7·20”郑州特大暴雨洪涝灾害,全市因灾死亡失踪380人,直接经济损失409亿元[6]。日益严重的城市洪涝灾害是影响城市安全和健康有序发展的重要因素。城市洪涝问题受到了国家高度重视,已成为国内外研究的热点领域之一。城市暴雨洪涝模拟作为制定城市防洪减灾措施的重要依据之一,是城市洪涝致灾机理分析与暴雨洪涝预报的重要手段,如何提高城市暴雨洪涝模拟的精度与准确性已逐渐成为城市洪涝研究领域的难点与热点[7]。
目前国内外学者在城市暴雨洪涝模拟方面取得了一系列研究成果[8- 9],城市雨洪模型是研究暴雨洪涝问题的重要手段,常用的城市雨洪模型有SWMM、MIKE、Info Works ICM、HSP、STORM等[8- 10],其中由美国环境保护署(EPA)发布的免费开源软件SWMM不仅能模拟单一降雨事件,还可以对长期的降雨径流进行动态演算,利于二次开发,在城市降雨径流模拟中得到了广泛应用[11- 13]。常晓栋等[13]采用SWMM模型构建了山前平原型城市雨洪模型,分析子汇水区不同汇流方式及河道糙率对模拟结果的影响;侯精明等[14]基于SWMM模型构建了含低影响开发(LID)措施调控作用的城市雨洪模型,模拟不同重现期降雨下LID措施和传统开发情况下的径流控制及峰值削减效果;周云峰等[15]利用基于方差分解的Sobol方法,计算不同雨强下SWMM中各参数对径流量、峰值流量以及峰现时间的灵敏度;赵刚等[16]将改进填洼模型与SWMM模型进行耦合,使改进后的模型可以快速模拟洪水淹没状况;栾清华等[17]提出了缺乏管网流量监测数据时城区暴雨径流SWMM模型的构建方法,提高了城区复杂下垫面数字化的精细化程度以及雨洪径流的模拟精度;朱治州等[18]提出了SWMM模型子汇水区划分中顾及多要素的城市地表汇水区分级划分法,结果表明基于该方法的划分结果基本符合实际汇水情况。SWMM模型构建过程中,经常会遇到城市雨水井节点资料难以获取等问题,而雨水井节点数据是影响城市暴雨洪涝模拟积水结果的重要因素。子汇水区是SWMM模型的水文计算单元,子汇水区划分方法的准确性是影响城市洪涝模拟的关键因素[18]。目前,SWMM模型的研究主要集中在低影响开发措施调控作用、模型积水深度计算改进、参数率定及灵敏度分析等方面,对模型的地表空间离散化和无资料时雨水井节点数据确定方法研究较少。
本文提出考虑城市实际空间信息的汇水区分级划分方法和雨水井节点数据确定方法,以武汉市青山区为研究区域,构建SWMM模型;采用2场实际暴雨渍水数据对模型参数进行率定与验证,并将基于空间信息分级划分法的模拟结果与传统泰森多边形法和水文分析结合泰森多边形法的模拟结果进行对比分析。
1 暴雨洪水管理模型的改进
1.1 SWMM模型
SWMM模型是1971年由美国环境保护署设计研发的动态降水- 径流模拟模型,已广泛应用于城市暴雨洪涝研究以及排水系统规划、分析和设计[19]。该模型把研究区域划分为一系列子汇水区,子汇水区接受大气中的降水,一部分降水下渗进入不饱和土壤,一部分降水在子汇水区中形成地表径流,地表径流经雨水井节点进入排水管道汇流,排水管道输送径流至排水口排出。
子汇水区是该模型的水文计算单元,通常划分为透水区域、蓄水和无蓄水不透水区域。子汇水区中降水下渗进入不饱和土壤区域有3种模拟方式:霍顿(Horton)方程、格林- 安普特(Green- Ampt)模型和径流曲线数法。霍顿方程比较适合城区,且率定参数少,在国内外得到了广泛使用,本研究采用霍顿方程进行下渗计算[13]。地表径流量进入排水管道运动有3种演算模型:恒定波法、运动波法和动力波法。动力波法适合任何排水管网较短时间步长模拟,结果准确,适用性较强,本研究采用动力波法进行管网汇流计算[11,13]。
1.2 城市子汇水区划分
1.2.1 基于空间信息的汇水区分级划分
致谢:本文得到了广东省有色地质勘查院粤北分院肖元贵、郭兰宣高级工程师的大力支持;广东省有色金属地质局王军同志在图件及文稿修改方面给予了大量帮助,在此谨表衷心的感谢!
(1) 基于研究区域下辖行政区域和排水管道流向的一级汇水区划分。行政区域是国家为了进行分级管理而实行的区域划分,各行政区负责管辖区域内的防汛排涝及雨季防汛抢险[20],街道等下辖行政区域是分级管理的基础单位。城市子汇水区进行划分时,首先应根据出水口及排水管道流向进行一级汇水区初步划分[17];其次,应该基于研究范围内下辖行政区域对已划分的一级汇水区进行再次划分,完成一级汇水区的精细划分。
(2) 基于排水管道和城市道路的二级汇水区划分。城市雨水一般是沿着城市道路汇流,并通过雨水井进入排水管网,汇流至排水管道出水口排入河渠或通过泵站排入江河[21]。在一级汇水区划分的基础上,首先应以排水管道为边界将每个汇水区进行二级汇水区初步划分;其次,根据城市快速路、主干路、次干路、支路边界线对已初步划分的二级汇水区进行再次划分,完成二级汇水区的精细划分。
(3) 基于住宅、商业、绿地公园等地块的三级汇水区划分。住宅、商业、绿地公园等地块是城市规划管理部门根据某地具体用途划分的用地基本单元。在二级汇水区划分的基础上,参照高清影像图和现场调研获取的地表建筑物边界,以各个住宅小区、商场、绿地公园等为边界将相应二级汇水单元进一步划分为三级汇水区;住宅、商业等地块的排水管道和雨水井往往沿住宅、商业区内的道路铺设,对于占地较大的住宅、商业区等,根据区域内部道路对其汇水区进行再次划分,完成三级汇水区的精细划分。最后,根据研究区域内管道排水流向确定相邻汇水单元的上下游关系,完成模型子汇水区划分(图1)。
1.2.2 基于泰森多边形法的汇水区划分
美国气候学家Thiessen提出的泰森多边形法是对空间平面的一种剖分,其特点是多边形内的任何位置离该多边形的样点距离最近,离相邻多边形内样点的距离远,且每个多边形内有且仅有1个样点。基于泰森多边形法划分的汇水区保证了每个子汇水区有且仅有1个对应的雨水井节点,且雨水井节点到对应的子汇水区距离最短。这种方法相对简单,比较节省时间,被广泛应用于城市雨洪模型中汇水区的划分。
1.2.3 基于水文分析结合泰森多边形法的汇水区划分
泰森多边形法虽然应用广泛,但没有考虑管道流向和地形分布等情况[18]。基于水文分析结合泰森多边形法的汇水区划分则对这一情况进行了考虑。该方法首先结合地形和排水管道采用水文分析工具初步划出较大的子流域;其次在已划分的子流域内,根据雨水井节点的分布,采用泰森多边形法对每个子流域进行细分;最后,将划分的汇水区与遥感影像图进行叠加,根据出水口及排水管道流向对划分的汇水区进行调整,使汇水区的流向与实际排水流向一致,完成模型子汇水区的划分(图2)。为了使汇水区划分的结果更加接近真实流向,本研究在基于水文分析划分子流域时,将排水管道作为河渠水系,通过AGREE算法对DEM数据进行校正[22]。基于水文分析结合泰森多边形法所划分的子流域考虑了管道流向和地形分布等情况,但未考虑土地利用类型变化。

图1 基于空间信息的汇水区分级划分步骤Fig.1 Catchment hierarchical partition based on the method of spatial information
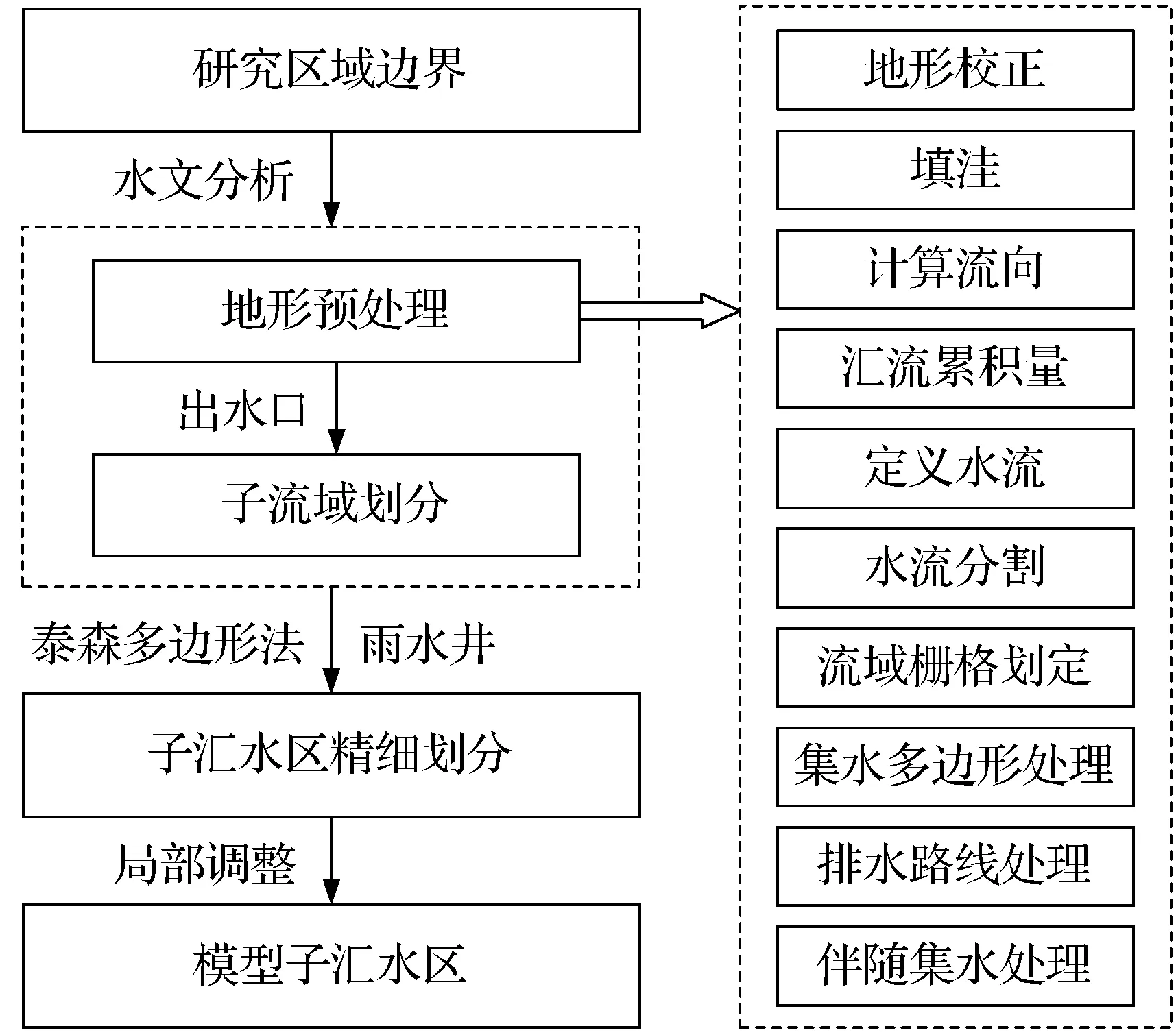
图2 基于水文分析结合泰森多边形法的汇水区划分步骤Fig.2 Catchment partition based on the Thiessen polygon method combined with hydrological analysis
1.3 雨水井节点数据确定
子汇水区的地表径流通过雨水井节点进入排水管网,雨水井节点是连接子汇水区与排水管网的重要枢纽。雨水井节点数据往往不完整且难以获取,对城市洪涝的高精度模拟提出了挑战,本文针对研究区域雨水井节点资料短缺现象,根据《室外排水设计规范:GB 50014—2006》(2016年版)[23]和少数已知的雨水井节点数据,对无资料的雨水井节点数据进行计算,尽可能地使计算结果更加接近真实情况。
(1) 确定节点位置。节点位置确定的原则为2段管渠相交处和2段道路相交处设置节点。每个排水管网系统管道末端设置1个出水口,每个子汇水区对应1个节点。每个子汇水区对应的封闭区域出口处根据需要设置节点。
(2) 节点数据计算。SWMM模型构建中需要确定各节点的内底标高与最大深度。节点的最大深度可通过节点地面高程与内底标高之差计算得到。采用研究区域1∶1 000高精度DEM数据提取各节点的地面高程。排水管道沿排水流向按照一定的设计坡度沿程递减铺设,节点的内底标高可根据排水管道长度、规范规定相应管径的最小设计坡度[23]和已知的上游节点内底标高进行计算。管网的最小设计坡度是由排水管道的管径决定的,如0.4 m管径对应的最小设计坡度为0.001 5,1 m管径对应的最小设计坡度为0.000 6[23]。节点内底标高的计算公式如下:
hj=hi-lijSij
(1)
式中:hj为节点j的内底标高;hi为j上游节点i的内底标高;lij为连接2个节点的管道长度;Sij为连接2个节点的管道最小设计坡度。
(3) 节点数据确定。根据节点地面高程和节点内底标高计算节点深度,节点深度应符合设计规范。规范规定,管顶最小覆土深度宜为人行道下0.6 m,车行道下0.7 m,即雨水井深度不应小于管径加埋深,检查井深度不应小于1.8 m。根据排水流向对各节点深度依次进行检查,对不符合的节点深度进行管道坡度的调整,其中,对于地形起伏变化较大的地区以城市道路坡度作为管道坡度,使所有节点深度均满足规范要求,得到各节点的最终数据。
1.4 积水深度计算
基于SWMM模型的城市暴雨洪涝模拟,能够获取研究区域内各溢流节点的积水流量过程,但无法直接获知各溢流节点的积水深度。当研究区域内各溢流节点产生积水时,SWMM模型默认节点上部积水区为蓄水设施,待排水系统非完全充满时,蓄水设施的积水再随之排出[7,19]。结合节点积水产生机理和相关参考文献[7,21],将节点积水水体等效概化为圆锥体,进而推导计算各溢流节点积水深度。
各溢流节点积水深度计算的步骤:
(1) 将各溢流节点上部的积水区域概化为圆锥体的蓄水设施,蓄水设施的体积为
(2)
式中:V为圆锥体的体积;d为积水深度;s为平均坡度。
(2) 将各溢流节点的积水流量过程作为该溢流节点蓄水设施的进流量。
(3) 计算各溢流节点蓄水设施的深度变化,即为该溢流节点的积水深度变化过程。
2 应用案例
2.1 研究区概况
研究区域主要位于武汉市青山区,西起罗家港,北临长江,东接东湖港与武丰湖,南至友谊大道,为城市水系统研究的典型片区(图3)。研究区域还包括了友谊大道向北与东湖港向南的少部分洪山区,该区域范围较小,在本研究中作为青山区冶金街道部分计算。研究区域雨水主要通过罗家路、港西和港西二期泵站排入长江,少部分直接排入罗家港、东湖港等渠道。武汉市青山区是武汉市的重工业城区、国家重要钢铁生产和化工基地。城区的下垫面由高低不一的建筑物和复杂的道路所组成,用材又多为砖、水泥、钢筋和沥青等,下渗能力较低,容易造成城市内涝积水现象[24]。
2.2 模型构建
根据当地的排水管网和地形资料,构建研究区域暴雨洪涝模型。由于实测资料获取的限制,本文只获得了研究区域内荆州街、随州街、工业路、工业一路和工业三路部分雨水井与出水口数据,针对缺少实测资料的雨水井节点,采用雨水井节点数据确定方法计算各节点内底标高和最大深度。根据获得的节点资料,将研究区域内圆形排水管道的雨水井最大深度限制为4 m,排水管涵的雨水井最大深度限制为6 m。从荆州街、工业路等已知节点沿管道流向依次计算未知的雨水井数据,得到的出水口底部标高与实测数据基本一致,且计算的节点深度和管道坡度均符合设计标准,表明该方法在雨水井节点数据缺失的城市暴雨洪涝模拟中具有一定的可靠性和适用性。为了保证研究结果的准确性,3种方法的节点数据均采用基于空间信息的汇水区分级划分法所得结果,即3种方法划分的节点数据和管道数据均相同,为790个节点和792条管线。
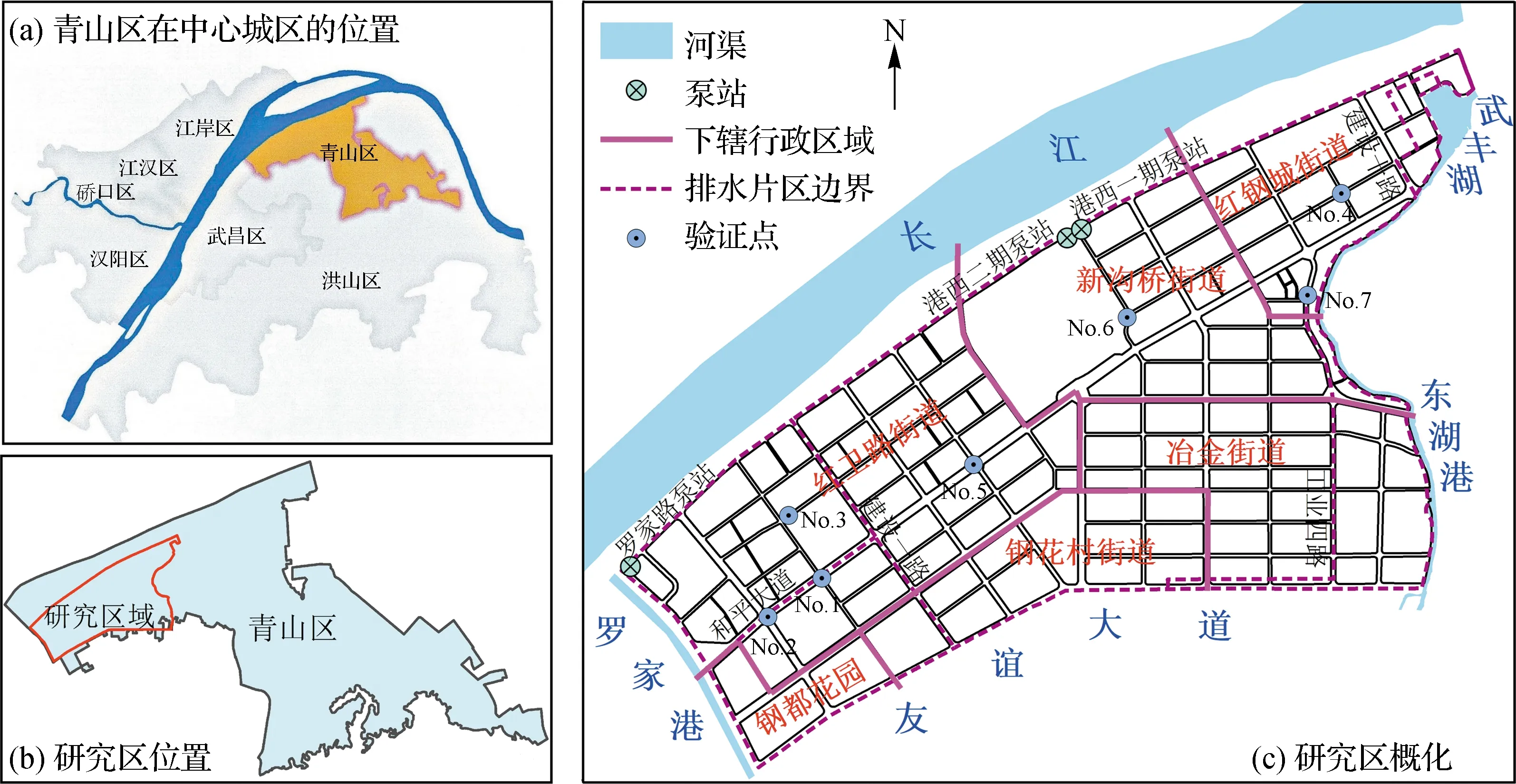
图3 研究区域概况Fig.3 Sketch of the study area
基于空间信息的汇水区分级划分法在研究区域的具体应用,包括3个步骤:首先根据出水口及相应连接的排水管线将研究区初步划分为罗家港北部排水片区(和平大道以北及建设一路以西的标注范围)、罗家港南部排水片区(和平大道以南及建设一路以西的标注范围)、港西排水片区(建设一路以东、工业四路以西及建设十路以西的标注范围)、武丰湖排水片区(建设十路以东的标注范围)以及东湖港排水片区(工业四路以东的标注范围)(见图3)。在初步划分的排水片区基础上,依据研究区域中各街区范围(图3),完成一级汇水区的划分。其次,根据排水管道和城市道路对已划分的一级汇水区进行二级汇水区深层次划分。最后,根据住宅、商业、绿地公园等地块进行三级汇水区的精细划分,最终把研究区域划分为705个子汇水区(图4(a))。基于泰森多边形法的汇水区划分,采用泰森多边形工具,根据雨水井节点的分布实现了汇水区的划分,研究区域划分结果见图4(b)。基于水文分析结合泰森多边形法的汇水区划分,首先利用水文分析工具实现较大子流域的初步划分,其次利用泰森多边形法在每个子流域内实现汇水区的精细划分,研究区域划分结果如图4(c)所示。
3种方法划分的子汇水区均符合SWMM模型的建模需求,但三者划分的结果具有明显的差异。以基于空间信息分级划分法、水文分析结合泰森多边形法和泰森多边形法划分的局部区域(对应图4(c)红色框线的标注范围)结果为例进行对比(图4(d))。基于空间信息分级划分法所得汇水区考虑了行政区域、建筑物边界、排水管道等对汇流过程的影响,水文分析结合泰森多边形法考虑了地形分布、管道流向和雨水井分布,泰森多边形法只考虑了雨水井分布。例如S85,和平大道与园林巷2条道路为两街道行政区域分界处,不同建筑物分布在2条道路的两侧,且和平大道道路中间铺设了高架桥墩,存在2根平行排水管道,属于不同排水片区,分级划分法所得结果体现了这一情况,水文分析结合泰森多边形法仅考虑了管道流向情况,泰森多边形法则未对此情况进行考虑,因此基于空间信息分级划分法所划分的汇水区更符合实际汇流情况。
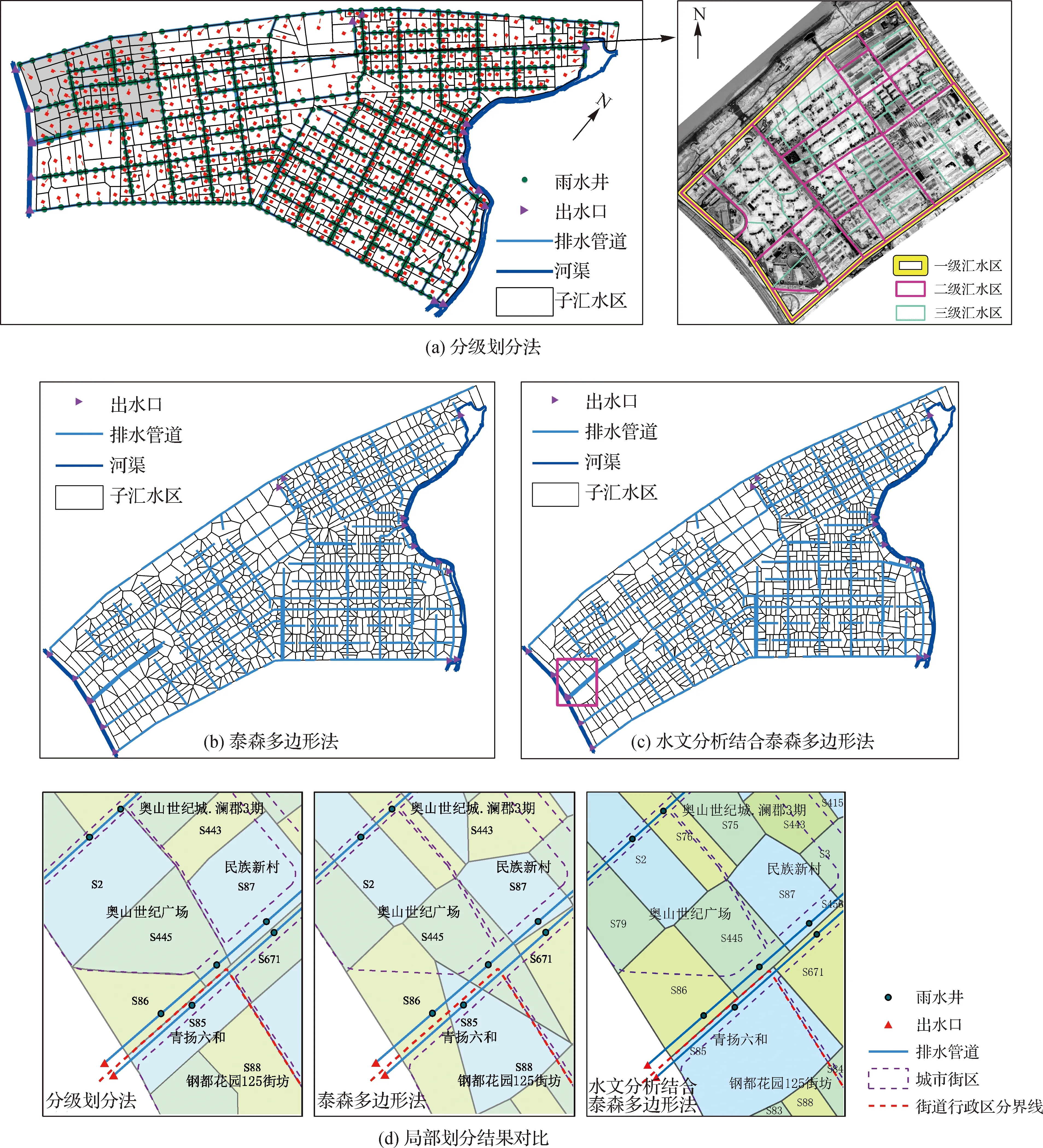
图4 不同汇水区划分方法的结果对比Fig.4 Comparison between the results using different subcatchment division methods
3 模型率定与结果分析
3.1 参数率定
2016年7月武汉市遭遇了严重的城市洪涝,6月30日至7月7日降雨量达到武汉市气象记录周降雨量最高值(图5(a))。本文选取2016年6月30日至7月3日(简称20160702)、2016年7月5—7日(简称20160706)2场降雨和5年一遇3 h/24 h降雨作为模型参数率定和验证的降雨过程。2016年7月2日24 h降雨量153.1 mm,相当于5年一遇24 h降雨量(162 mm);7月6日24 h降雨量241.5 mm,相当于20年一遇24 h降雨量(249 mm)。参照《武汉市排水防涝系统规划设计标准》(2013年版)[25],采用武汉市暴雨强度公式结合芝加哥雨型生成5年一遇3 h降水;根据武汉市24 h暴雨逐时雨量分配,得到20160702、20160706 场次降水情景和5年一遇24 h降水情景,如图5(b)所示。
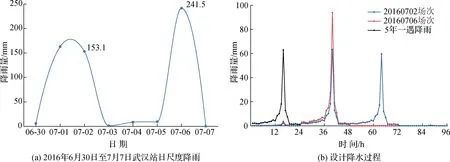
图5 研究区域实测与设计的降雨量过程Fig.5 Measured and designed rainfall hydrographs in the study area
采用综合径流系数作为目标函数对模型参数进行初步率定[11,26],选取2016年7月2日、2016年7月6日实际暴雨渍水点和2016年青山区5年一遇3 h(88 mm)/24 h(162 mm)降雨渍水风险图,对模型参数进行详细率定与验证。管道长度、子汇水区面积、特征宽度等参数可通过实际测量或计算得到。地表漫流曼宁系数、洼地蓄水、管渠曼宁系数等经验参数,根据SWMM模型用户手册[19]和相关文献查询[13- 15]确定各类参数范围,以综合径流系数作为模型参数校准的目标函数,使模型子汇水区径流系数符合规范[25];反复调试各类参数,直至模拟的积水点与实际渍水点最为接近,模型参数率定结果如表1所示。

表1 模型主要参数率定
3.2 结果分析
根据2016年7月2日和2016年7月6日暴雨渍水点资料,选取和平大道三弓路口(No.1)、和平大道园林路口(No.2)、旅大街(No.3)、建设九路(No.4)(见图3)为20160702场次暴雨内涝典型验证点,选取和平大道三弓路口(No.1)、和平大道建三路口(No.5)、建设五路桥洞(No.6)、沿港路(No.7)(见图3)为20160706场次暴雨内涝典型验证点,对比各验证点模拟的最大积水深度与实际积水程度,结果如表2所示。根据《武汉市排水防涝系统规划设计标准》(2013年版)[25]可知,路段积水平均深度h≤0.15 m为轻度积水,0.15 m

表2 溢流点最大积水深度对比
武汉市水务局发布了2016年青山区5年一遇3 h(88 mm)/24 h(162 mm)降雨渍水风险图,对比相同设计降雨条件下模型模拟的溢流点与风险图渍水位置分布情况,结果如表3所示。3种方法划分的汇水区所模拟的溢流点与渍水风险图对比,研究区域内未模拟出的渍水地区大体上有旅大街建设二路附近、建设六路附近(和平大道与红钢三街中间段)和红钢二街建设十路附近等,虽模拟结果与渍水风险图存在一定的差异,但模型计算的溢流点与实际渍水位置分布总体上是一致的。基于空间信息分级划分法划分的汇水区,模拟产生的220个溢流点中有80.0%的溢流点位置与渍水风险图相符;基于水文分析结合泰森多边形法划分的汇水区,模拟产生的225个溢流点中有76.4%的溢流点位置与渍水风险图相符;基于泰森多边形法划分的汇水区,模拟产生的226个溢流点中有77.4%的溢流点位置与渍水风险图相符。3种方法划分的汇水区所模拟的溢流点位置分布基本相同,但基于空间信息分级划分法所得汇水区模拟的积水深度与实际淹没程度更一致。因此,基于空间信息分级划分法所得汇水区的模拟结果精度更高,为数据匮乏地区的城市洪涝模型建立提供了参考。

表3 模拟溢流点统计
根据《武汉市排水防涝系统规划设计标准》[25],结合雨水管渠设计暴雨重现期和城区防涝标准要求,采用武汉市暴雨强度公式结合芝加哥雨型生成5 a、10 a、20 a、50 a和100 a重现期下2 h短历时暴雨,进行不同降雨情景下研究区域内涝积水模拟,结果如图6所示。随着降雨重现期的增大,3种方法划分的汇水区所模拟的积水时间和积水量逐渐增加,基于空间信息分级划分法所得汇水区模拟的积水量与其他2种方法模拟的积水量差呈增加的趋势。不同降雨重现期下,基于空间信息分级划分法所得汇水区模拟的溢流点个数和积水量总体相对较少。3种方法划分的汇水区所模拟的溢流点积水量大多数小于100 m3,约占溢流点总数的48%以上,随着降雨重现期的增大,占比总体呈减少趋势。降雨重现期不超过20 a时,3种方法划分的汇水区所模拟的溢流点积水时间主要集中在10~30 min,约占溢流点总数的41%以上,随着降雨重现期的增大,占比在逐渐减少。其中,5 a降雨重现期下,模拟的溢流点积水时间基本上未超过1 h,且发生积水的节点占比较低,表明5年一遇暴雨情景下的积水对研究区域影响程度相对较小;10 a和20 a降雨重现期下,积水时间在1~2 h的溢流点约占溢流点总数的17%~30%,且模拟的溢流点积水时间均未超过2 h,表明在10年一遇和20年一遇暴雨下研究区域的局部地区内涝积水较为严重。降雨重现期大于20 a时,3种方法划分的汇水区所模拟的溢流点积水时间主要集中在1~2 h,约占溢流点总数的41%以上,表明研究区域遭遇大于20年一遇暴雨时会发生严重的内涝积水,且随降雨重现期的增大,内涝积水程度越严重。特别是100 a降雨重现期下,溢流点积水时间最长超过2 h,总溢流量超过40万m3,可引起严重灾情,在一定范围内给行人和车辆安全带来影响。
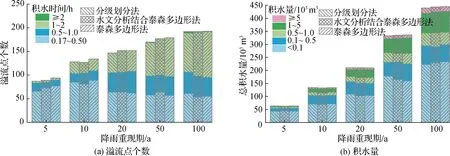
图6 不同降雨重现期下积水模拟Fig.6 Simulated numbers of overflow points and ponding volumes under the rainfall hydrographs with different return periods
4 结 论
针对城区复杂下垫面和雨水井数据缺失情况,分别提出了基于实际空间信息的汇水区分级划分法和雨水井节点数据确定方法。以武汉市青山区为研究对象,采用2场实际暴雨渍水数据对模型参数进行了率定与验证,主要结论如下:
(1) 雨水井节点数据确定方法是根据《室外排水设计规范:GB50014—2006》(2016年版)[23]和已知的雨水井节点数据对无资料的雨水井节点数据进行计算,计算的雨水井节点深度和管道坡度均符合设计标准,且采用实测数据进行了验证,表明该方法在雨水井节点数据缺失的城市暴雨洪涝模拟中具有一定的可靠性和适用性。
(2) 基于空间信息分级划分法、水文分析结合泰森多边形法和泰森多边形法所划分的汇水区,8个典型验证点模拟的最大积水深度中分别有100%、63%和75%验证点与实际渍水程度相符,模拟的溢流点中分别有80.0%、76.4%和77.4%的溢流点位置与5年一遇降雨渍水风险图相符。基于空间信息分级划分法所得的汇水区比较符合真实汇水情况,且模拟的结果比其他2种方法更加准确。
(3) 5年一遇降雨重现期下,3种方法划分的汇水区所模拟的积水对研究区域影响程度相对较小,但遇到高于此重现期的暴雨,局部地区会出现不同程度的内涝。降雨重现期大于20 a时,模拟的溢流点积水时间主要集中在1~2 h,会发生严重的内涝。特别是100 a重现期下,溢流点积水时间最长超过2 h,可引起严重灾情,在一定范围内给行人和车辆安全带来影响。
