基于物理学科大概念层级理论的教学思考

袁宁

摘   要：形成物理学科大概念是知识向素养提升的关键环节，利用物理概念与物理方法的总结、归纳、升华形成物理思维﹑建立物理学科大概念，进而形成学科观念，培养学科素养，凸显大概念能够提高物理教学的“纲领性”与学习知识的“策略性”。通过对“力的合成与分解”的矢量运算关系进行深度分析和归纳，最终呈现出二者的优选性与实效性，帮助学生在具体的力学模型处理中能够实现程序性向策略性的转变，最终培养“降维”分析的物理思维。

关键词：学科大概念;物理思维;力的合成与分解;降维

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2022）4-0063-4

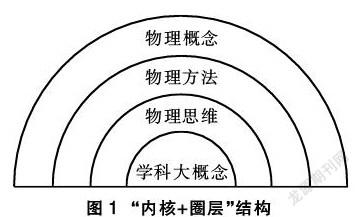
学科大概念是指反映学科本质及其特殊性的﹑构成学科框架的概念。从知识层级关系角度，大概念是奥苏贝尔所说的上位层级，最具抽象性﹑概括性﹑包容性，对于其他知识具有统摄和生发的功能，是一种“内核+圈层”结构（图1）[1];从认知角度，大概念是学科思维方式的升华﹑学生认识水平的提升，是整合所学知识中的一根红线，由独特的视角建构知识上位，逐步形成真正意义上的物理学科素养。

1    处理静力学模型矢量运算的常见思路

以常规斜面木块模型为例，简要呈现以下三种思路。

例1 木块静止在粗糙斜面上，已知斜面倾角为θ，重力加速度为g，木块质量為m，研究木块所受摩擦力f及弹力N的大小。

（1）平行四边形定则——力的合成解析。在力的合成过程中，按照物体最终动力学状态的需求，将N、f与G合成为等效合力F与G平衡。其中F为主观力，G﹑N﹑f为客观实际力，如图2（1）所示。

（2）平行四边形定则——力的分解解析。在力的分解过程中，按照物体最终的平衡需求，将重力可以分解为与N﹑f共线反向的两个正交分效果力Gx与Gy。其中，Gx与Gy为主观力，G﹑N﹑f为客观实际力，如图2（2）所示。

（3）三角形定则——力的合成解析。三角形矢量图解法中，G﹑N﹑f为客观实际力，如图2（3）所示。

由以上三种常见思路，可以发现合力﹑分力不全与实际力对应，实际力是由力学模型的受力环境定性得出的，因此无法从实际受力这一单一因素来确定合成与分解的优选性。下面从数模构建来探寻二者的关联性。

高中数学平面向量模型遵循二维线面运算法则，以三角函数为核心建立运算关系，可以分为以直角三角形建模的正余弦解析运算和以任意角三角形建模的正余弦定理解析运算。而对于任意角的数模分析，学生很难掌握一般化思维并进行理论解析，所以在高中阶段常见的思路是围绕直角的建构展开，将一般性二维向量化解为特殊方向的共线代数运算。如图3所示，将向量的二维运算关系统一到特殊方向单一维度的共线代数运算后，呈现出任意角与特殊直角的统一性与相通性。

由以上简单证明可以得出力的矢量运算中合成与分解两种思路在解析策略方面的相通性：合成是将多个力变共线力代数运算（一维），分解是将非共线多力变为两组特殊方向共线力合成（一维）——多维变一维。

3    优化选择，二元归一

由以上模型证明可以看出，力学模型解析过程涉及一种重要的物理思维——降维法。我们将例1的斜面木块模型的受力环境进行开放性修改，增加受力分析和题目解析的综合型，来更深层次体会降维降解这一重要的物理思维在解题中的应用。

例2 如图4所示，一质量为 M、倾角为θ的木楔，静置在水平面上，一质量为m的木块在该木楔的斜面上恰好可以匀速下滑。如果用与斜面成α角的恒力 F 作用在木块上，木块恰好匀速上滑，木楔保持静止。

（1）求木块与木楔接触面的滑动摩擦因数μ;

（2）当α=θ时，求匀速上滑过程中恒力 F 的大小;

（3）求第（2）问中木楔受到地面的摩擦力大小。

（2）以沿斜面向上为正方向，当α=θ时，斜面上木块受力分析及正交分解如图6所示。

由以上解析可以看到此题的标准解析过程对细节分析及书写能力要求较高。导致很多学生在题意理解的基础上还是大量丢分，是因为在进行分解处理时，虽然将非共线四力通过正交分解化为特殊方向的共线力代数运算，但是需要分解两组外力G与F，很容易出现函数关系误判导致分析错误。那么，当我们从降维的总体需求思考，此题难度关键在于力多（多于三个），如果能够进行一定的降维处理，再进行解析（三个力），解析的过程会更加简洁。

如图7、图8提供的第二种思路：

由图6中的几何条件可证明 γ=φ=2θ（γ为G与FR的夹角），则由三角形定则得出摩擦力 f 与支持力 N 的等效力 FR，FR=Gsin2θ。

由第（1）问可知FR与N1的夹角为θ，由于N1与斜面垂直，可知φ+α。 因α=θ，则可知 FR与拉力 F 垂直，则实际物体受力情况可等效为三力平衡，如图8所示。

在此方法中可以发现，主要的分析瓶颈在于作图和几何条件证明，一旦完成边角关系的分析，第（2）问的总体解析难度大幅度减小。所以从降解的角度，第二种思路利用合成FR去降维，最终建构矢量三角形进行数理分析，比第一种正交分解的思路更加简洁清晰，这种方法优选于正交分解法。而学生往往会更习惯用正交分解法的原因在于没有理解合成与分解的最终目的是相同的——降维分析，谁更简化就用谁，同时对学生数学的几何建模能力也提出更高要求。

（3）由于木块与木楔均处于平衡状态，将两者整体处理，对二元系统进行受力分析（图9）。

当然，第（3）问若首先利用第（2）问中的合成FR降维（图10），再利用牛顿第三定律将f1'与N1'等效为FR'，最终过程（过程略）与整体法的正交分解难易度相似，达到相同优选性。

現代心理学将知识共分为三类：陈述性知识﹑程序性知识﹑策略性知识[2]。在建立力学模型过程中受力分析定性解决了模型第一层级的力源问题，学生利用三种特性力的陈述性知识在实际力学模型分析过程中实现了陈述性向程序性的提升;当我们得出实际受的所有力时，将涉及到更高的层级要求——定量描述。通过上述的梳理旨在由程序性知识向更高层级的策略性知识进行探寻，从而得出力的矢量运算中所蕴藏的重要的物理学科思维（降维分析），从而在合成与分解的选择方面能够更快捷地确定优选思路。

图11展示的物理学科知识的建构逻辑是由内而外逐步外显的，大量门类繁多、体系细化的知识系统的背后是极简化的物理大概念与物理思维在主导和引领;而对应的物理知识的认知过程是渐进和螺旋式的，由外而内，层层剖析，不断深化，最终形成思维与上位概念。两者相互映射的闭环逻辑最终形成了物理学科的总体建构与认知层级。

参考文献：

[1]程力，李勇.恢复高考40年物理考试内容改革述评[J].中国考试，2017（9）：1-10.

[2]郭玉英，姚建欣，张玉峰，等.基于学生核心素养的物理学科能力研究[M].北京：北京师范大学出版社，2017.

（栏目编辑    蒋小平）