一道立几试题的解法赏析及变式拓展

刘海涛

(安徽省芜湖市第一中学，241000)

一、试题呈现

题目如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2BC=2CD=2,P为四边形ABCD所在平面外一动点,且PA=PB,∠APB=90°,设M为PD的中点,则CM的值为______.

这是笔者所在学校高三的一道模考题,试题结构简单明了,形式上为求线段的长度问题,主要考查空间线面的平行与垂直关系、解三角形等知识,体现了逻辑推理、直观想象、数学运算等核心素养的综合考查.笔者发现该题内涵丰富,题中并未说明平面PAB与平面ABCD所夹角的大小,点P为空间中一动点,于是点M亦为动点,但为何线段CM长度却为定值呢?现将对该题的剖析与读者分享交流.

二、解法探究

分析1要说明CM的长度为定值,因为不知二面角P-AB-D的大小,所以无法得到线段PC,PD的长度,难以在∆PCD中直接解得线段CM长度.而由条件可确定等腰Rt∆PAB各边的长度,故考虑利用平行关系转化到∆PAB中求解.

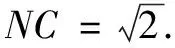
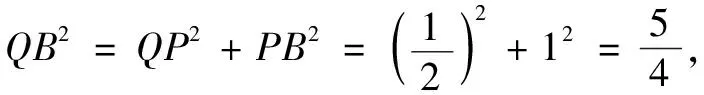
评注本题的解题策略是将动直线CM放入一个相对确定的平面∆PAB内,达到“以静制动”的解题效果.

分析2基于解法1,注意到线段MN为∆PAD中对应边PA的中位线,容易判断知∆MNC的具体形状,由余弦定理即可求出线段CM的长度.

评注解法2实为解法1的优化,将长度为定值的线段CM构造为一确定三角形的一条边,直观展示出线段CM的长度不受二面角P-AB-D大小的影响.实际上,立体几何中有很多这样的例子,比如将矩形ABCD沿着其一条对角线AC翻折,无论翻折成多大的二面角B-AC-D,所构成的三棱锥D-ABC的外接球球心始终为线段AC中点,球的半径始终为线段AC长的一半.

分析3利用空间向量解决立体几何问题,可大大降低空间思维的难度.因此考虑建立空间直角坐标系来分析点P,从而得出点M的情况.

评注引入空间向量解决立体几何问题,避开了传统方法中对平行、垂直、角、距离等问题所进行的大量繁琐的“定性分析”,只需建立空间直角坐标系进行“定量分析”,实现了几何问题的代数化处理.

三、命题背景剖析

四、变式

变式1如图6(1),在矩形ATCD中,AD=2DC=2,B为TC的中点,将∆TAB沿AB翻折,使得点T到达点P的位置,连结PD,得到如图6(2)所示的几何体,设M为PD的中点,则CM的值为______.

变式2在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2BC=2CD=2,P为四边形ABCD所在平面外一动点,且PA=PB,∠APB=90°,设M为PD的中点,则动点M的轨迹的长度是______.

变式3在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2BC=2CD=2,P为四边形ABCD所在平面外一动点,且PA=PB,∠APB=90°,设点M为PD的中点,则直线CM与平面ABCD所成角的正弦值的最大值为______.