利用基本不等式求最值的常用变形策略
2022-05-09平丽敏
平丽敏
(江苏省扬州市新华中学,225009)
“不等式”在新教材苏教版必修一的第三章,教学要求是让学生再次理解不等式的概念,掌握不等式的性质,进而研究基本不等式的证明和应用.不等式也是高考的热点和重点内容,能有效考查学生的数学抽象、逻辑推理和数学运算等核心素养,其地位举足轻重.利用基本不等式求最值时应具备“一正,二定,三相等”的三个条件,但很多情况下直观上看问题时都不满足上述三个条件,需要作适当变形,创造条件后再利用基本不等式求解.高一学生在学习这部分内容时,对如何变形常常感到困惑.本文结合实例介绍一些常用的变形策略.
一、双变量问题消元法

分析本题是求和的最小值,但直观上看问题并不满足基本不等式的条件,其积不是定值.当条件和目标的关系不清晰时,可用消元法减少变量,使关系更简单.


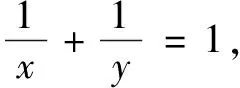

评注如果待求式中含有两个或多个变量,有时可以根据变量的关系进行消元,达到减元求解的目标,化解问题的难点.
二、乘“1”之后代换法


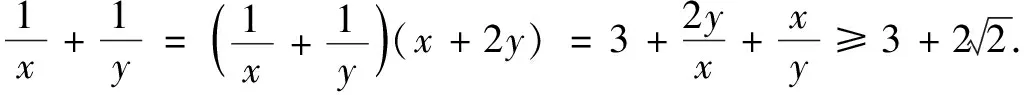
变式若正数x,y满足x+3y=5xy,求3x+4y的最小值.

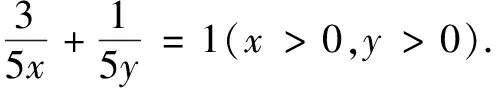
评注“1”的代换法是凑成基本不等式条件的关键,也是利用基本不等式求最值的常用方法之一.
三、引进常数配凑法
例3已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为( )
(A)2 (B)4 (C)6 (D)8
分析问题要求和的最小值,但条件不是积为定值,无法直接运用基本不等式求解.若注意到条件等式为二次三项式,因式分解可将条件变形为(x+1)(2y+1)=9的形式,再将目标函数写成(x+1)+(2y+1)-2的形式,就为利用基本不等式求最值做好了铺垫工作.



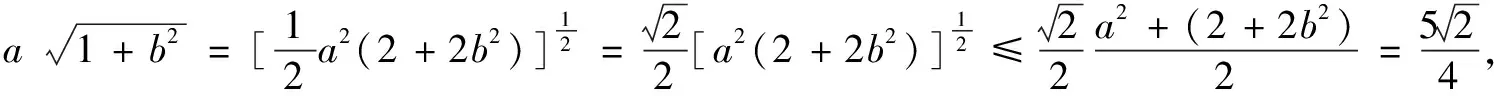
评注为了制造“定值”这一条件,有时需因式分解,有时要根据已知式和待求式的结构特点用添加法配凑出需要的一个常数.
四、简化分母换元法

分析目标式的分母不是单项式,若把分母看作一个整体,即用换元法,可使目标式和条件式的关系更清晰.



分析注意到分母是二次多项式,分子是一次多项式,要使问题简化,可把分母分解成两个一次的乘积,换元后分母就是单项式了,此时利用基本不等式可求解.


评注抓住题目中的结构特征,对分母实施双换元,就可以利用“1”的代换求出最值.
利用基本不等式求最值,关键在于“拆、拼、凑”,将条件式或者待求式变形为“和或积”为定值.当然,每一题目的解法不一定唯一,我们需要尽可能掌握好通性通法,才能以不变应万变.
