直线参数方程下两点间距离公式的微课探究——一次纠错的意外收获

仰宏丽

(安徽省无为第一中学,238300)

一、教学背景

在安徽省芜湖市2021-2022学年度第一学期高三年级的教育教学质量监控的文科数学试卷上,有这样一道题:

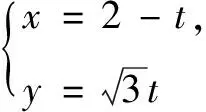
(1)求直线l的普通方程和曲线C的直角坐标方程;

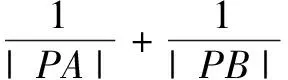
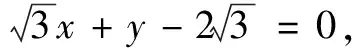
这是一道考查坐标系与参数方程相关内容的常规题,试题难度虽然不大,但第(2)问的解答却不尽如意.很多同学给出了如下的解答:

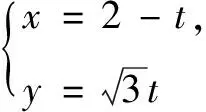
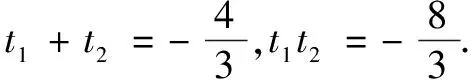
学生为什么会出现这样的错误呢?笔者认为主要是学生对直线的参数方程的相关知识发生遗忘,只会套用公式.那如何纠错呢?回归课本无疑是最好的策略.为此,笔者准备就此题在班上展开一次微课教学.

二、微课教学探究

首先，借助希沃白板投影了错误答案.

师:如此求解对吗?

生1:不对.

师:哪里不对?

大家陷入了沉思,笔者见时机已经成熟,请同学们拿出教材,重新阅读直线的参数方程这一节的内容.

师:通过阅读,大家对刚才的问题有何感想?

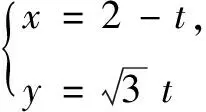
师:生2的意思是说题设中的直线可以有两种不同形式的参数方程,它们形式不同时,参数的含义也不同.

师:由教材可见,当直线l经过点M0(x0,y0),倾斜角为α时,它的参数方程可以表示成

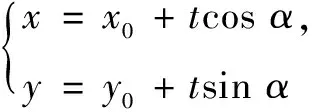
①

我们称① 式为直线l参数方程的标准形式,此时参数t有明确的几何意义.那大家能不能将此问题一般化呢?

生3:经过点M0(x0,y0),倾斜角为α的直线l的参数方程还可以表示成

②

师:可以将② 式称为直线参数方程的一般形式.② 式与① 式的区别在于参数t没有明确的几何意义,所以应用参数的几何意义解题时,我们通常选择① 式.如果题目给出的是② 式,我们可以把② 式转化为① 式.

错解的同学恍然大悟,原来是直线的参数方程选择不当导致的错误.

问题似乎已经得到了圆满解决,这时突然有学生提出了新的问题.

师:这个问题问得很好!大家看看该如何解答?

过了片刻,有同学提出如下的解答.

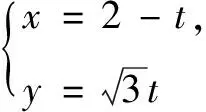
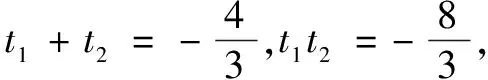
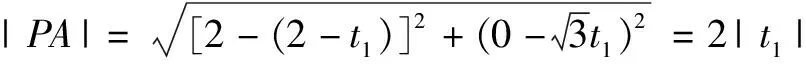
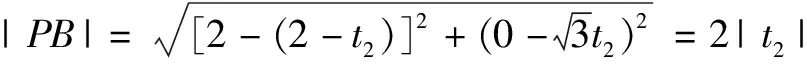
两种解法都能很好的回答学生4所提出的问题.

师:解题中不仅要会求PA，PB的长度,有时还要会求AB的长度.形式① 下两点间距离公式教材已经得到,那么形式② 下的直线上任两点A，B的距离公式如何表示呢?

师生共同探讨:设点AB在参数方程形式② 下所对应的参数为t1,t2,则其直角坐标分别为A(x0+at1,y0+bt1),B(x0+at2,y0+bt2).于是

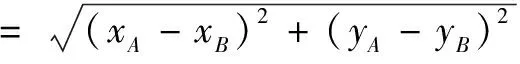
特别地,当a2+b2=1时,有|AB|=|t1-t2|,这便是标准参数方程形式① 下两点间的距离公式.

三、教学感悟

一次纠错,我们不仅让学生明白了他们错在何处,而且还意外收获了直线参数方程在一般形式下两点间的距离公式.这表明我们在一线教学时,一方面要引导学生认真阅读教材,透彻领会教材内容内在的深刻含义;另一方面要有不止于教材的研究意识,用科学的态度和方法专研教材,使所学内容有效拓展、融会贯通.