一道高考压轴题的探究历程与教学建议

2022-05-09刘再平

高中数学教与学 2022年7期

关键词：阿基米德压轴切线

刘再平张琪

(陕西省汉中中学,723000)

一、试题呈现

如图1，已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.

(1)求p;

(2)若点P在圆M上,PA,PB是C的两条切线,A,B是切点,求∆PAB面积的最大值.

此道是2021年全国乙卷理科圆锥曲线压轴题第21题,试题表述简洁,问题设置循序渐进,有一定的梯度. 第(1)问比较基础,考查圆外一点到圆上距离的最小值,根据圆的几何性质即可求出p的值;第(2)问显然需要用参数表示出∆PAB的面积,最后再求面积的最值,是此道压轴题真正的压轴点.

二、解法探究

求最值可以从函数、均值不等式和三角函数三个常见的视角出发,梳理解题活动的思维导图如图2,从而获得下列通性通法.

由点P在切线上,得x1x0-2y1-2y0=0,且x2x0-2y2-2y0=0,则点A,B的坐标满足方x0x-2y-2y0=0,即直线AB的方程为x0x-2y-2y0=0.

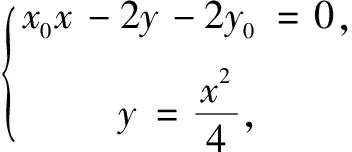
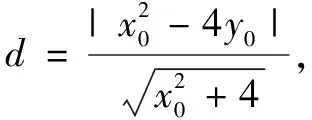
解法2设点P(cosα,-4+sinα),切线方程为y=k(x-cosα)-4+sinα,与x2=4y联立,可得

x2-4kx-4sinα+4kcosα+16=0.

令Δ=0,得k2-kcosα+sinα-4=0.故切线PA,PB的斜率k1,k2满足k1+k2=cosα,k1k2=sinα-4,即点P(k1+k2,k1k2).

评注解法1通过设点的坐标将三角形面积表示出来,使问题转化为二次函数的最值问题;解法2利用参数方程将三角形的面积转化为三角函数最值问题,其中还是需要借助二次函数的性质解题.因此,上述两种方法都属于解决此类问题的通法.

三、本质探究

在上述压轴题中,∆PAB称为阿基米德三角形.阿基米德(公元前287年——公元前212年),古希腊伟大的哲学家、物理学家,并享有“数学之神”的称号.为了纪念他，将抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形.

性质2直线AB的方程为(x1+x2)x-2py+x1x2=0.

性质4直线AB过抛物线内一定点C(xc,yc)时,点P的轨迹方程为xcx-py-pyc=0.特别地,当点C为抛物线的焦点F时,点P的轨迹为抛物线的准线,且PA⊥PB,PF⊥AB,且(S∆PAB)min=p2.

性质1至3仿上述解法1和解法2类似可证,这里从略.下面给出性质4的简证如下.

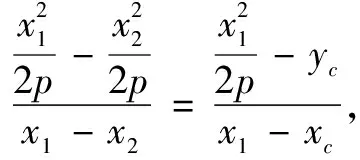
xcx-py-pyc=0.

四、试题简解

运用阿基米德三角形的性质3,此道压轴题即可获得如下简解:

五、性质运用

1.在高考题中的运用

(2)设∆ABM的面积为S,求S的最小值.

2.在自招题中的运用

例2(2010年清华大学自招题)F为抛物线y2=2px的焦点,过点F的直线l与该抛物线交于A,B两点,直线l1,l2分别是该抛物线在A,B两点处的切线,l1,l2相交于点C,设|AF|=a,|BF|=b,求|CF|.

3.在竞赛题中的运用

例3(2015年湖北省高中数学竞赛题)过直线x-2y+13=0上一动点A(点A不在y轴上)作抛物线y2=8x的两条切线,M,N为切点.求证:直线MN恒过一定点.

简解不妨设直线MN恒过一定点P(x0,y0),由阿基米德三角形性质4,可知点A的轨迹方程为y0y-4(x0+x)=0,即4x-y0y+4x0=0.此直线方程与x-2y+13=0等价,由待定系数法可得x0=13,y0=8.故直线MN恒过定点P(13,8).

(1)求证:直线AB过定点;

(2)求∆PAB的面积S的最小值,以及取得最小值时点P的坐标.

简解(1)不妨设直线AB恒过一定点M(x0,y0),由阿基米德三角形性质4知点P的轨迹方程为x0x-(y0+y)=0,即x0x-y-y0=0.此直线方程与y=x-2等价,由待定系数法得x0=1,y0=2.故直线MN恒过定点M(1,2).

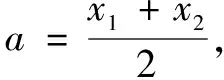
六、教学建议

1.夯实双基,提高数学运算能力

圆锥曲线问题充当压轴题的角色已经屡见不鲜,然而圆锥曲线压轴题并不是高不可攀.因为圆锥曲线解答题一般设置二至三小问,一般来说每问之间联系紧密,梯度明显,循序渐进,第一问往往立足基本知识,所以学生理所应当在日常的数学学习中夯实圆锥曲线的双基;第二、三问往往充当着压轴的地位,对学生的逻辑推理能力,特别是数学运算能力要求较高.如本文所阐述的2021年全国乙卷理科压轴题压轴第二问,通过认真审题,大部分学生应该都知道需要用参数表示出三角形的面积,然而三角形面积的表示并不容易,无疑对学生的运算素养要求较高. 所以教师要善于创设问题情境,将有关问题转化为运算问题,明确运算对象,确定运算思路,合理选用运算法则,培养学生的数学运算素养.

2.适当拓展,积极开展探究活动

查阅近十年的全国卷圆锥曲线解答题,不难发现很多题都有着丰富的数学背景.如本文所述的阿基米德三角形背景.所以教学中教师要善于超越具体知识与基本技能,深入到数学思维层面,适当拓展,积极开展探究活动,促进学生深度学习.然而,拓展探究并非易事,章建跃博士提出的如下探究 “基本套路”,值得借鉴.