基于改进的樽海鞘群算法的电力负荷经济调度策略

李玲玲，陈文泉，冯 欢

（1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学河北省电磁场与电气可靠性重点实验室，天津 300130）

电力负荷经济调度问题的优化能够提升发电厂的能源利用率，降低发电成本，提高电力系统的经济性[1-2]。

文献[3]提出了一种基于改进的粒子群算法和遗传算法的混合算法来解决综合考虑等式约束和不等式约束的经济负荷调度问题。但该混合算法依然具有很强的随机性，未解决算法收敛能力差和寻优精度低的问题。文献[4]将Lambda迭代法与模拟退火算法相结合，通过增加多个搜索机制来提高算法求解经济负荷分配问题的精度，但该算法的求解速度较慢。文献[5]提出了一种改进的社会蜘蛛优化算法，有效地简化了原算法的控制参数，避免了早熟现象的出现，但是其最优解的质量较差。

本文以电力系统的燃料成本最小为目标，建立了电力负荷经济调度的动态模型。同时，针对以往研究中存在的算法收敛速度慢、寻优精度差等缺点，提出了改进的樽海鞘群算法（improved salp swarm algorithm，ISSA），将Levy飞行策略[6]以及非线性收敛因子引入原算法。其中，Levy飞行策略可以扩大算法的搜索范围，进一步提升算法的寻优能力；非线性收敛因子提高了算法的局部搜索能力和收敛速度。在算例分析中，将ISSA得到的结果与粒子群算法（particle swarm optimization，PSO）、遗传算法（genetic algorithm，GA）得到的结果进行比较，以验证ISSA的性能。

1 电力负荷经济调度动态模型

电力负荷经济调度问题是一个非线性优化问题[7-8]。它的目标是在满足系统负荷需求和发电机实际运行约束包括功率平衡约束、输出功率约束、斜坡率约束和禁止操作区域限制的情况下，找到燃料费用最小时的机组最优组合[9]。

1.1 目标函数

该问题的主要目标是在满足各种等式和不等式约束的同时，使燃料成本最小化，满足电力系统在一定时期内的负荷需求。电力负荷经济调度问题的目标函数可以表示为：

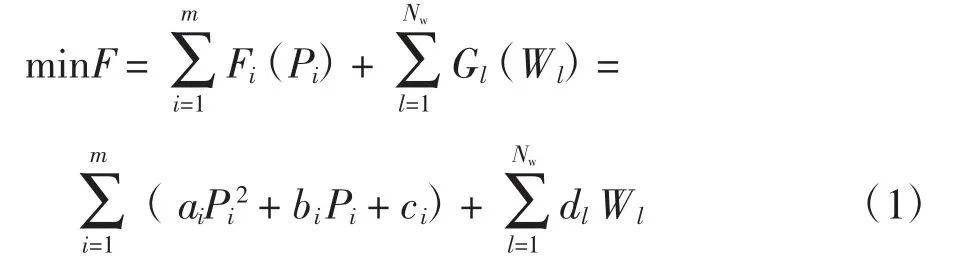
式中：F为燃料费用；Fi为第i个火力发电机的成本函数；Gl为第l个风力发电机的成本函数；ai、bi、ci为第i个火力发电机的成本系数；Pi为第i个火力发电机的输出功率；Wl为第l个风力发电机的输出功率；m为提交给操作系统的火力发电机组的数量；NW为风力发电机的数量；dl为风电场运行和维护的平均成本系数，该系数表示风电场每产生一单位的风电所花费的平均维护费用。

1.2 约束条件

为了更有效地优化电力负荷经济调度问题，通常假设发电机组的输出功率是固定的[10]。实际上，所有联机的发电机组的运行范围都受到其斜坡速率的约束，以限制发电机组在2个相邻时间段内的输出功率的变化。此外，蒸汽阀操作或轴承振动会造成发电机输入-输出曲线中出现禁止操作区域，这将会大大降低发电机组的性能，所以，在实际运行过程中应避免发电机组在这些区域进行操作。综上所述，发电机的运行条件复杂，要实现经济安全运行，必须考虑约束条件。

（1）功率平衡约束：

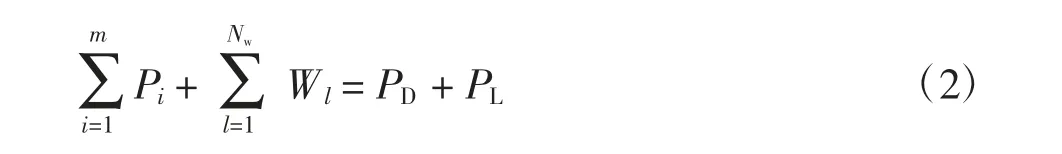
式中：PD为总负荷需求；PL为线路损耗，其值为输出功率的函数，可用B系数表示为：

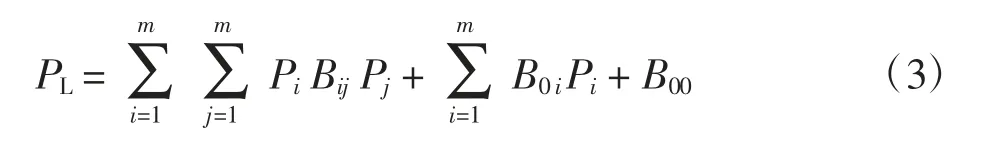
式中：Bij、B0i、B00均属于B系数，表示系统运行中的线路损耗。B系数详见文献[11]。在系统运行中，线路损耗要保持在较低水平，以减少燃料费用。

（2）火力发电机输出功率约束。每个单元的输出功率必须在其最小值和最大值之间。如果输出功率太大，会加速发电机组老化，缩减机组寿命；如果输出功率太小，发电机组没有得到充分利用，会造成资源浪费[12-14]。

式中：Pi为第i台发电机组的输出功率；Pi，min为第i台发电机组的最低输出功率；Pi，max为第i台发电机组的最高输出功率。

（3）风力发电机组输出功率约束

式中：Pav为风电场出力的最大值。

（4）斜坡率约束。发电机组的斜坡率约束是指机组发电过程中，发电功率变化范围的上限与下限[15]。具体如下：

式中：Pi(t-1)为第i台机组在前一个时间间隔的发电量；Ui和Di分别为第i台发电机组输出功率波动的上限和下限。本文将输出功率约束与机组斜坡率约束相结合，产生新的约束条件，即式（7）。若机组的输出功率能够在该范围内，即认为输出功率同时满足机组的输出功率约束和斜坡率约束：

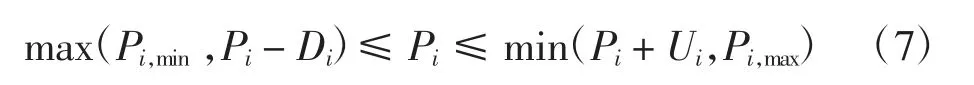
（5）禁止操作区域约束。每台发电机都有其发电能力限制。此外，一个典型的热单元可能有运行中的蒸汽阀，或轴承的振动，这可能会导致干扰，并导致输入-输出性能曲线的不连续，称为禁止操作区域[16-17]。为防止发电机组运行在禁止操作区域内，发电机组的作业区域描述为：

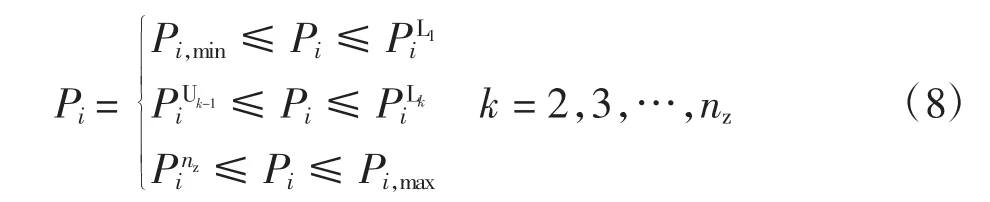
式中：PiLk和PiUk分别为发电机组i的第k个禁区的上限和下限；PiUk-1为发电机组i的第k-1个禁区的上限；nz为第i台机组禁止操作区域的数量。

2 樽海鞘群算法及其改进算法

樽海鞘群算法（SSA）是最近由Mirjalili等[18]提出的仿生算法之一。SSA模仿了樽海鞘在深海中高效导航和觅食时的群体行为。

2.1 樽海鞘群算法

在传统的樽海鞘群算法中，樽海鞘群体被划分为领导者和追随者，分别建立了相应的数学模型。领导者位于樽海鞘群的前端，并且领导者在搜索空间中引导其他群体向着目标移动。追随者是群体中的剩余个体，他们跟随群体的领导者。群体的目标是特定搜索空间中的食物源，记为G。对于d维搜索空间，用二维矩阵Sn×d定义所有樽海鞘在群体中的位置，其中n为樽海鞘的个数。矩阵S中的每个元素si，j对应于第i个樽海鞘在第j维搜索空间中的位置。

（1）在优化过程中，樽海鞘群体中领导者的位置根据食物来源进行更新，更新方法为：

式中：Gj为食物在第j维中的位置；uj和lj分别为第j维的上下限；r1、r2、r3均为参数，其中r2和r3是区间[0，1]上均匀分布的随机数，r1的更新方法为：

式中：t为当前迭代次数；T为最大迭代次数。

（2）在优化过程中，樽海鞘群体中追随者的位置更新方法为：

式中：2≤i≤n。式（9）和式（11）通过将食物源替换为全局最优的群体来模拟樽海鞘搜索食物的群体行为。但是，在优化问题中，全局最优是未知的。所以，当前获得的局部最优值可以被认为是当前的全局最优值，即在优化过程中全局最优值不断更新，并且通过搜索当前维度以及扩大搜索空间的方式，使得樽海鞘群不断向全局最优值移动。

佛像是佛、菩萨、罗汉、明王、诸天等像，不同的名对应不同的相。所谓如法，如为不变，引伸为恒定，也是依据法，尊重形象对于人心摄受的原理，让信众产生佛陀显前，教化众生的功效，如佛教教义之法，如佛像所传达信息之法，接引众生，见像起信。佛像要随时代而变，藏传佛像是藏族地区已经形成的对佛像的审美需求，是格式化的形态。汉传佛教是根据汉地人们的哲学观念、视觉习惯而形成的审美观念，形成的另一种格式化形态。

2.2 改进的樽海鞘群算法

2.2.1 Levy飞行策略

为了增加种群的随机行为从而提高种群的多样性，本文将Levy飞行策略引入樽海鞘群领导者的位置更新中。Levy飞行策略是一种非高斯随机过程，是服从莱维分布的随机搜索模式[6]。使用Levy飞行策略代替原方程中的随机数后，增大了领导者位置变化的范围，进而扩大了算法的搜索范围，避免算法陷入局部最优解。引入Levy飞行策略后的樽海鞘群领导者的位置更新方法为：

式中：d为位置矢量的维数；Levy（d）可表示为：

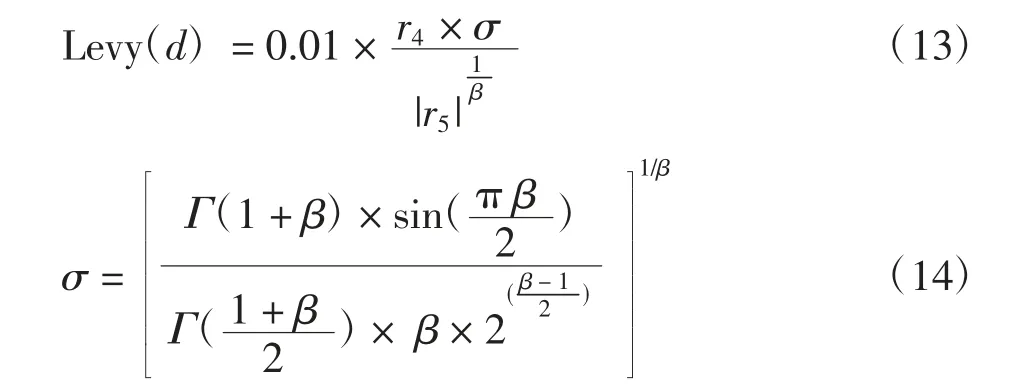
式中：r4和r5为区间[0，1]上的随机数；β为一个常量，通常设置为1.5；Γ（x）=（x-1）！。

改进算法通过引入Levy飞行策略，扩大了搜索范围，可避免算法陷入局部最优解，增强了算法的全局搜索能力。

2.2.2 非线性收敛因子

在传统的樽海鞘群算法中追随者的位置更新由当前个体与前一个体共同决定，为进一步提高算法的收敛能力，本文将非线性收敛因子引入原算法，并将当前最优解引入追随者的位置更新算式中。改进后追随者的位置更新方法为：

非线性收敛因子根据式（16）调整当前最优值在追随者更新公式中所占比重，使算法在当前最优值附近寻优，提升算法局部寻优能力以及收敛能力。非线性收敛因子表达为：

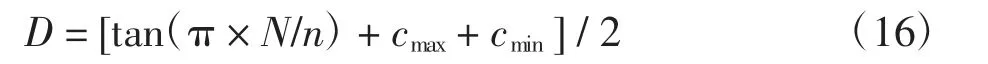
式中：N为最大迭代次数；n为当前迭代次数；cmin、cmax为2个学习因子。为了最大程度地提升算法求解负荷经济调度问题的收敛性，本文将cmin设置为0.000 04，cmax设置为1。非线性收敛因子以及当前最优值的引入能够大大提升算法的收敛能力，使算法能够迅速收敛到最优值。ISSA的算法流程如图1所示。

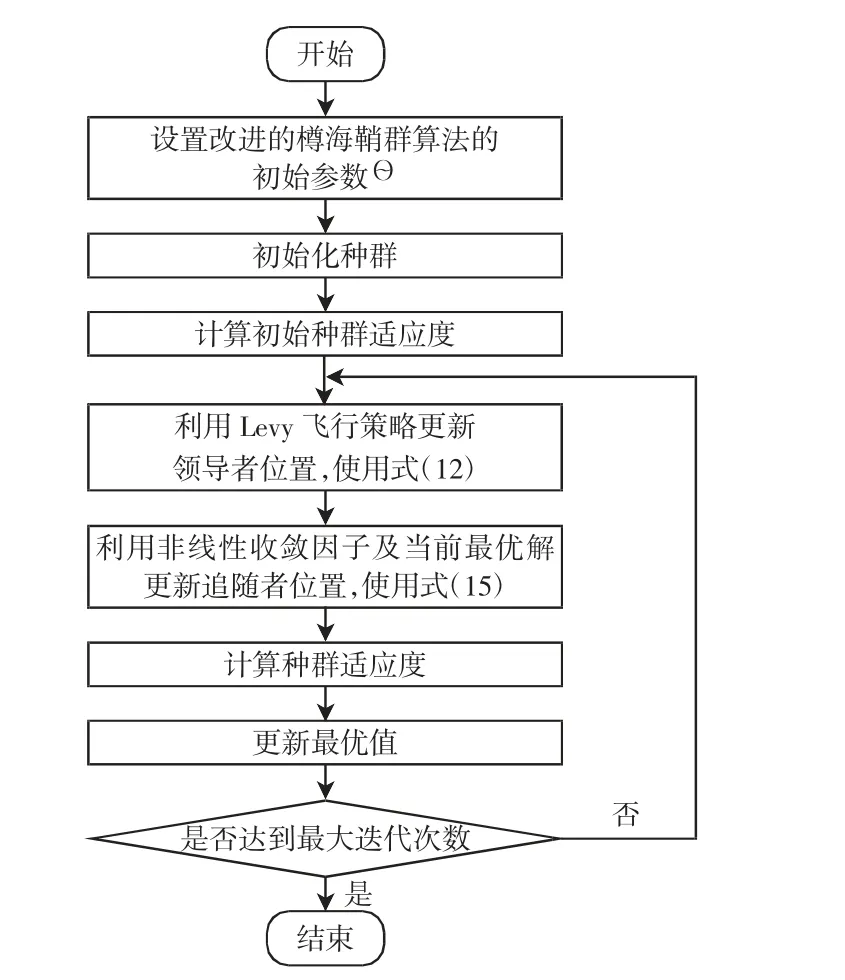
图1 改进的樽海鞘群算法（ISSA）流程图Fig.1 Flowchart of improved salp swarm algorithm

3 案例分析

3.1 基础数据

为了验证ISSA求解电力负荷经济调度问题的性能，本文将ISSA应用到两个电力系统中[19-21]。两个电力系统中分别包含6台[19-20]、15台[19，21]火力发电机组（以下分别称为六机组系统和十五机组系统），两系统的数据分别如表1和表2所示，两系统的负荷需求分别为1 263 MW和2 630 MW。

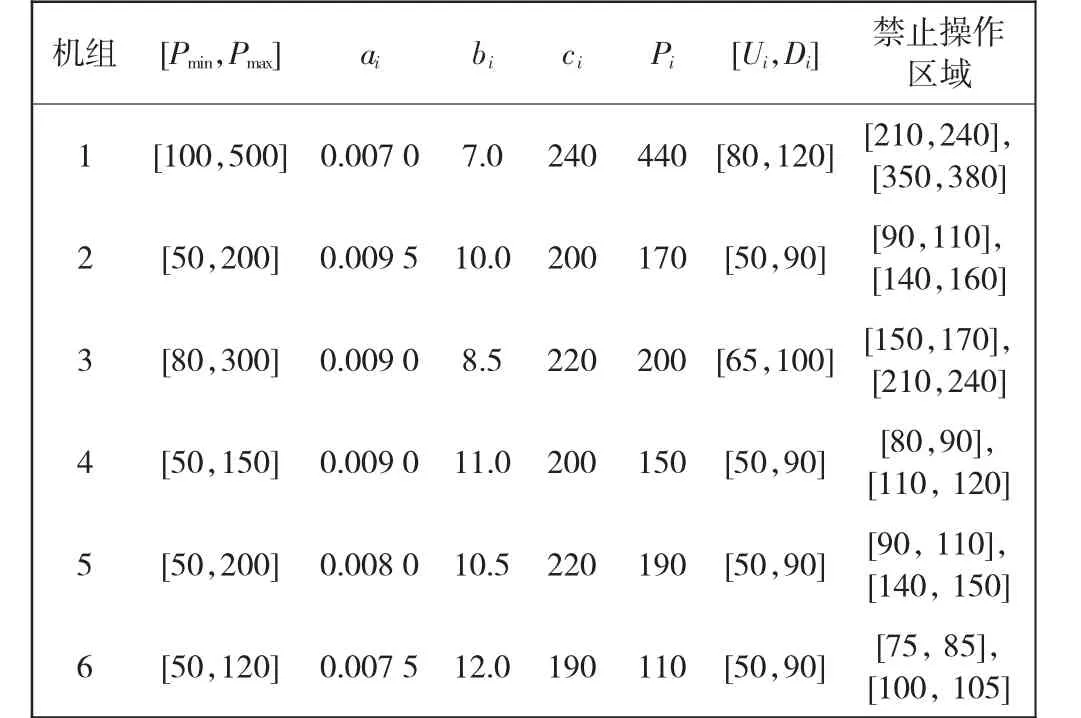
表1 六机组系统数据表Tab.1 Data table of six units system

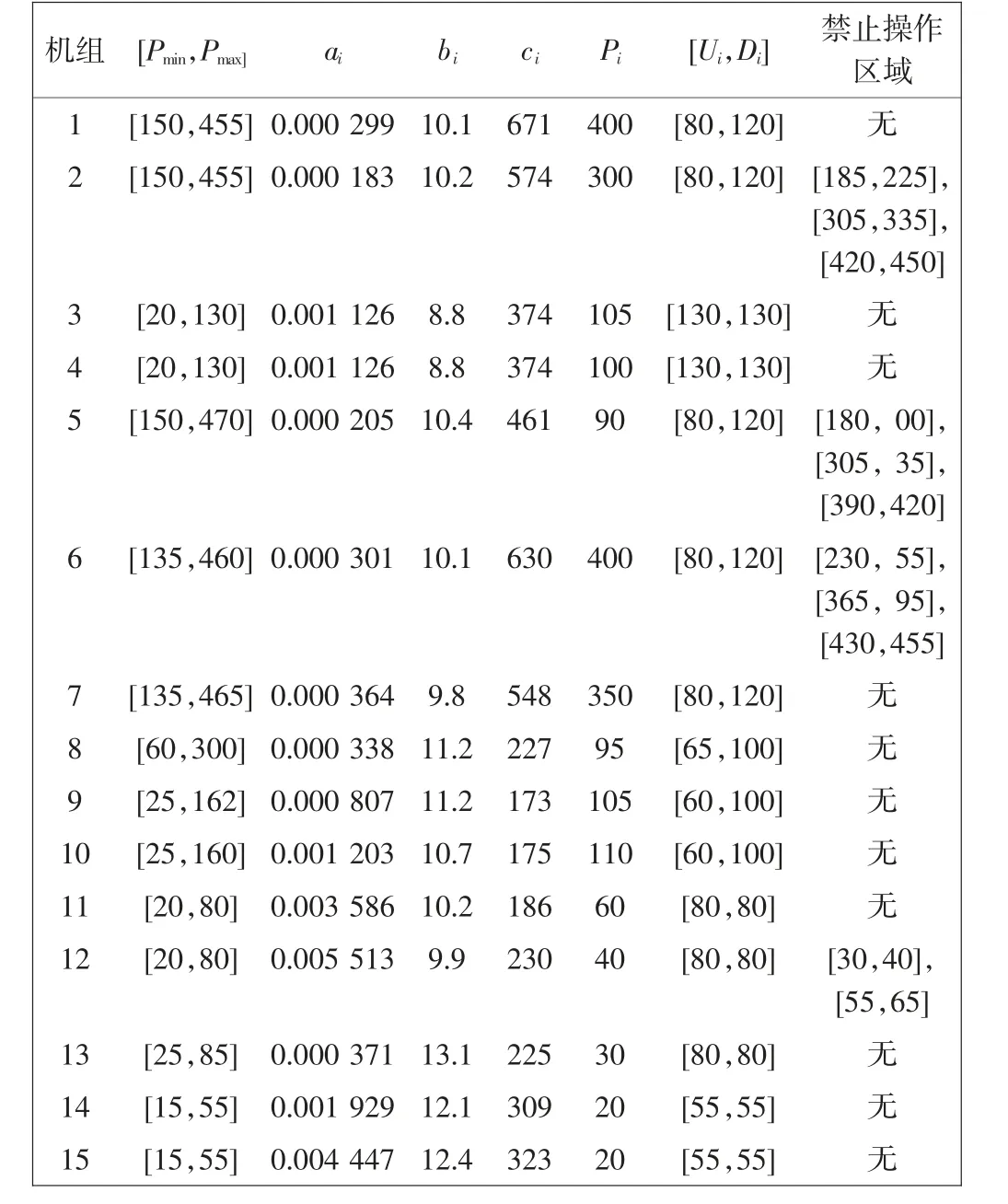
表2 十五机组系统数据表Tab.2 Data table of fifteen units system

本研究还在相应电力系统中加入风力发电机组。风电场的成本系数设置为7$/MW。在目前的技术条件下，风电总容量占所在电网容量的比例不能超过一定的值，一般认为是10%。因此，在这两个案例研究中，风力发电的功率份额按总负荷需求的10%进行处理。表2中部分机组不存在禁止操作区域，因此相关指标值为“空”。表1中数据来源于文献[19-20]。表2中数据来源于文献[19，21]。

3.2 算法性能分析

为了检验改进的樽海鞘群算法（ISSA）的性能，本文将之与传统的樽海鞘群算法（SSA）、粒子群算法（PSO）、遗传算法（GA）一并用来求解电力负荷经济调度问题，并将4种算法的计算结果进行对比分析。

3.2.1 六机组系统

上述4种算法应用于六机组系统时的计算结果如表3、图2和图3所示。

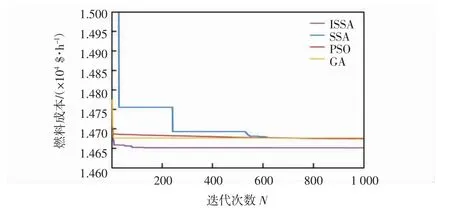
图2 六机组系统燃料费用最小化的收敛曲线Fig.2 Convergence curves of fuel cost minimization in six units system

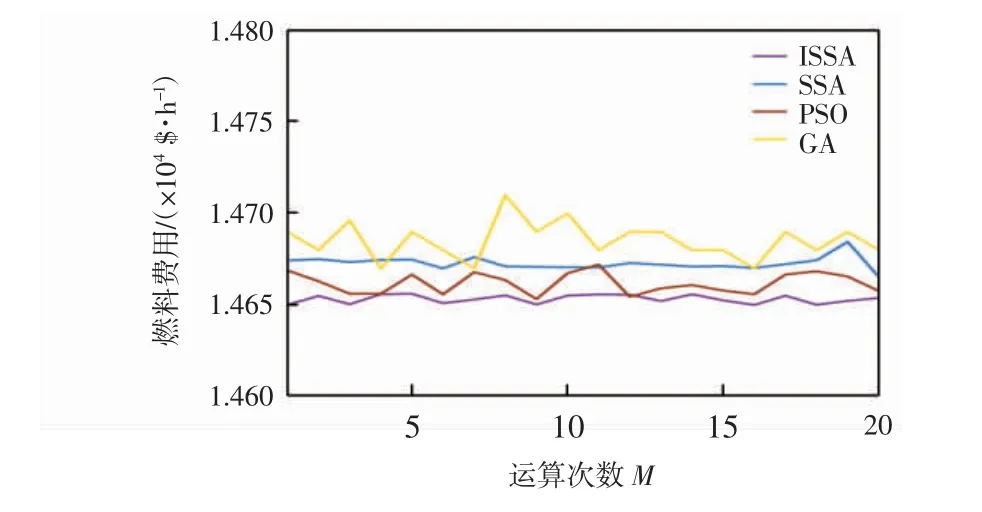
图3 六机组系统的燃料费用最优解Fig.3 Optimal solution of fuel cost in six units system

由表3可知，算法在确保各台发电机组的出力都满足各项约束的前提下，ISSA所获计算结果比SSA、PSO、GA更优，即燃料费用最低，线路损耗最小。改进的樽海鞘群算法得到的燃料成本费用比PSO、GA、SSA分别降低了0.14%、0.38%、0.15%。另外，与文献[19]、文献[20]分别采用人工免疫算法和改进型PSO所获得的关于六机组系统的最低燃料费用15 459$/h、15 453.50$/h相比，表3中由ISSA获得的14 652.67$/h明显更低，说明ISSA比上述各种算法能更好地解决六机组系统的电力负荷调度问题。

表3 六机组系统的燃料费用及各发电机组的出力Tab.3 Fuel cost of six units system and output of each generator unit

图2和图3则从另一侧面展示了ISSA的良好性能。由图2可以看出，ISSA的收敛曲线更为平滑，收敛速度更快，证明该算法有着良好的收敛效果。由图3可以看出，ISSA在20次计算中的求解结果波动最小，这说明ISSA比其他算法有着更好的稳定性。

3.2.2 十五机组系统

上述4种算法应用于十五机组系统时的计算结果如表4、图4和图5所示。

表4 十五机组系统的燃料费用及各发电机组的出力Tab.4 Fuel cost of fifteen units system and output of each generator unit

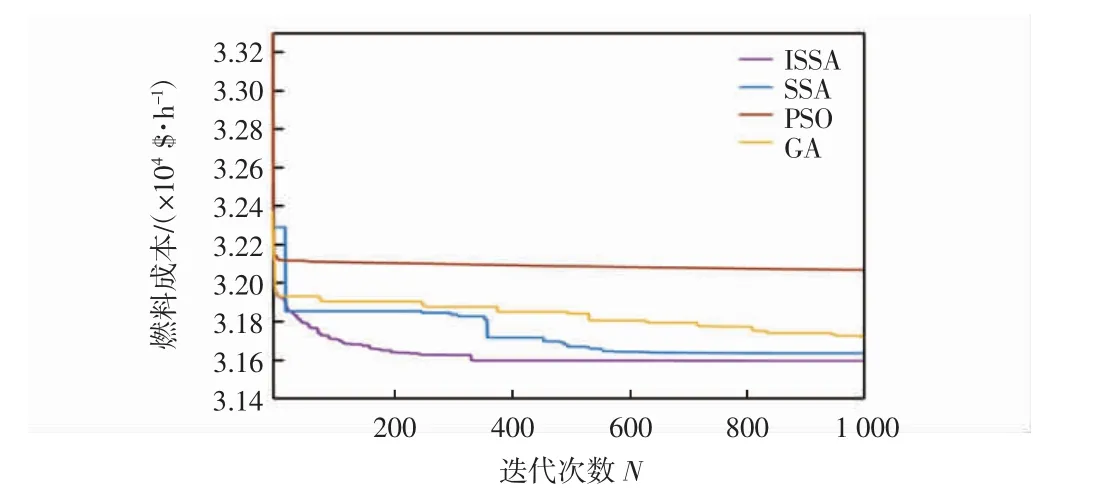
图4 十五机组系统燃料费用最小化的收敛曲线Fig.4 Convergence curves of fuel cost minimization in fifteen units system

与前文将4种算法用于六机组系统时的结论相同，ISSA在十五机组系统相关问题的求解中表现出比其他算法更好的性能。由表4和图4可知，ISSA得到的系统燃料费用最低，说明其优化效果最好，寻优能力最强。改进的樽海鞘群算法得到的燃料成本费用比PSO、GA、SSA分别降低了1.33%、0.39%、0.12%。另外，文献[19]和[21]分别采用人工免疫算法、改进的灰狼优化算法对十五机组系统的燃料费用最小化问题进行了求解，结果分别为32 873$/h、32 734.62$/h，明显大于ISSA得到的31 594.22$/h，说明ISSA能够比其他算法更有效地求解十五机组系统的电力负荷经济调度问题。

由图4还可以看出，ISSA的收敛速度比GA和SSA快、比PSO慢，但PSO过快的收敛速度和相对较差的优化结果证明其未能在效率和效果之间求得均衡，是算法早熟的一种表现，故其性能不如ISSA。图5中，ISSA的曲线最平滑、平坦，说明其稳定性最好。

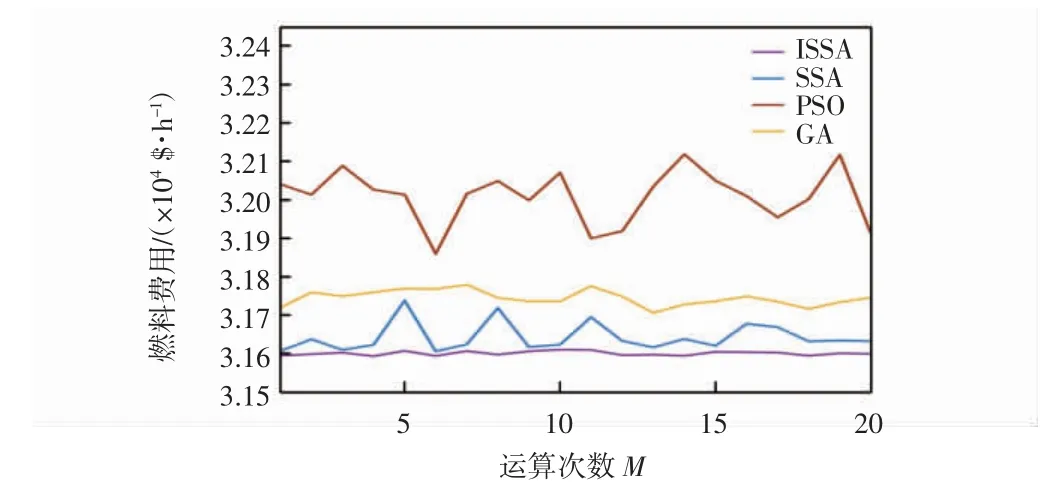
图5 十五机组系统的燃料费用最优解Fig.5 Optimal solution of fuel cost in fifteen units system

4 结论

（1）本文以燃料成本为目标函数，引入了功率平衡约束、发电机输出功率约束、斜坡率约束和禁止操作区域约束，最大程度地还原了动态电力负荷经济调度的数学模型。

（2）提出了改进的樽海鞘群算法（ISSA），使用Levy飞行策略代替原方程中的随机数，使领导者位置变化的范围更大，进而扩大了算法的搜索范围，避免算法陷入局部最优解；使用非线性收敛因子调整当前最优值在追随者更新公式中所占比重，使算法在当前最优值附近寻优，提升算法局部寻优能力以及收敛能力。

（3）将ISSA优化算法应用到六机组和十五机组系统的电力负荷经济调度案例中以验证算法的实际性能，并与SSA、PSO以及GA算法进行对比分析。结果表明，相比于其他3种算法，ISSA能够以较快的速度获得最低的系统燃料成本，对于六机组系统，ISSA的燃料成本费用比PSO、GA、SSA分别降低了0.14%、0.38%、0.15%；对于十五机组系统，ISSA的燃料成本费用比PSO、GA、SSA分别降低了1.33%、0.39%、0.12%。并且在多次计算中都能稳定地获得燃料成本的最小值，适宜用来求解电力负荷经济调度问题。

（4）在未来的研究中，会进一步完善电力负荷经济调度的建模，将光电等新能源以及需求响应加入模型中，并引入潮流方程等约束。同时，对ISSA算法进行相应改进，进一步提升其适用性。