基于RF-GA-SVM算法的施工升降机输入电压控制模型
2022-05-09徐伟雄高宗帅王莉静
郗 涛,徐伟雄,高宗帅,王莉静
(1.天津工业大学机械工程学院,天津300387;2.天津城建大学控制与机械工程学院,天津300384)
施工升降机是建筑工程中必不可少的施工设备,在超高层建筑的使用过程中供电电压一般为有级调节,即在低高层时使用的是380 V,在超高层时随能耗的增加使用690 V,但实际需要的输入电压远低于供电电压,造成了严重的电能浪费问题。针对以上问题,国内有人在控制方法方面做了研究。其中,文献[1]利用比例-积分(PI)自调整与模糊逻辑补偿的复合控制方法对控制系统进行改进,但PI自调整与模糊逻辑控制方法多适用于液位、压力、流量等控制系统,对电压的控制效果较差;文献[2]采用BP神经网络PID控制方法使电梯的运行更加稳定,系统动态性能有所提高,但BP神经网络算法的收敛速度慢且存在过拟合的问题,对于多因素影响的电压预测准确性较低;文献[3]采用模糊BP神经网络的电梯群控系统改善了运行效能,模糊控制改善了BP神经网络控制的准确性,但算法本身的特性限制了控制准确性的提高;文献[4]计算出能量目标函数,使用蚁群算法建立蚁群模型,并验证了算法在减少能耗方面是有效的,但蚁群算法的收敛速度较慢,对于电压的快速控制效果较差。虽然以上研究对电压控制进行了改进,但考虑的因素较少,算法的优良性较弱,没有从根本上改善问题,还有优化空间。
针对影响输入电压的多因素问题,本研究基于物联网平台采集的历史数据,考虑环境因素和能量传递中的多因素数据,提出一种基于数据挖掘的RF-GASVM输入电压的控制方法。利用随机森林算法(RF)计算各个因素的重要度,并根据计算结果进行因素选择,再将选取后的样本约简集合进行归一化处理,通过遗传算法(GA)对支持向量机(SVM)的参数进行优化,采用优化后的SVM算法进行回归计算,得到预测输入电压,并对预测和原始输入电压进行回归评价,分析该输入电压控制模型的准确性。
1 影响施工升降机输入电压的因素分析
1.1 外部环境影响因素
施工升降机多是露天使用,且使用时各地环境差别很大,因此,环境因素将对运行产生很大影响。其中,温度、风速、空气密度和瞬时风向是主要影响因素。风速、空气密度和瞬时风向将产生空气阻力,影响相对运动速度,空气阻力公式为:

式中:C为空气阻力系数;ρ为空气密度;S为物体迎风面积;V为物体与空气的相对运动速度。在考虑空气阻力时,施工升降机安装时的倾斜角会影响空气阻力的方向,所以安装倾斜角也是影响因素之一。
环境温度升高将使电机内部损耗增大,导致效率降低,影响电机的输出功率[5],在额定负载时,环境温度差(t2-t1)与电机温升差Δθ之间的简化关系为:

式中:θ为电机温升;K为等效的发热损耗系数。
1.2 能量传递过程中的影响因素
施工升降机的结构如图1所示。能量传递过程为供电电压经过滑触线传递到控制箱,控制箱通过变频器变电压和频率后输出到三相异步电机,电机再将转速和转矩传递给减速器,经过减速器降速度,提转矩,驱动齿轮齿条使吊笼运动。
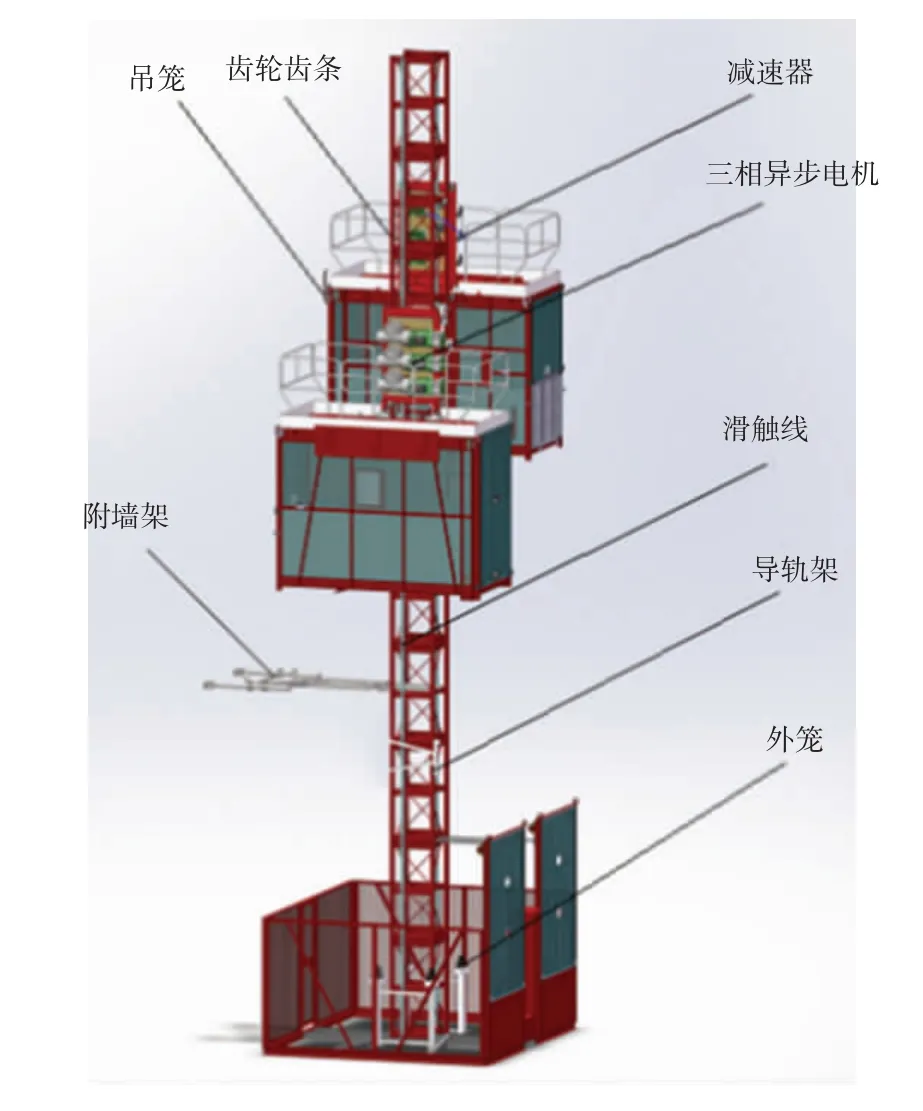
图1 施工升降机的结构Fig.1 Structure of construction elevator
滑触线随着运行高度变化以及电流的变化将产生压降,滑触线压降公式为:
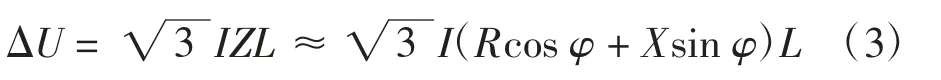
式中:I为负荷电流;Z为阻抗;L为滑触线长度;电阻R为电抗;cosφ为功率因数。
三相异步电机的温升产生的温度场对电机内部损耗有影响[6],转速和转矩对吊笼稳定运行有影响,转速公式为:

式中:f为供电频率;s为转差率;p为电机的级对数。
转矩表达式为:
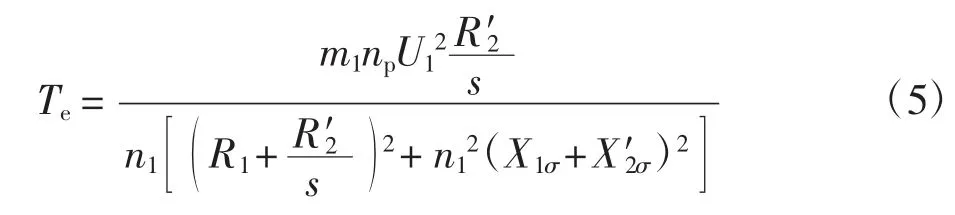
式中:m1为电机相数;np为极数;U1为额定电压;R1为相电阻;R'2为转子电阻;X1σ为漏抗;X'2σ为漏电抗;n1为同步转速。
减速器中的传动比、油压和温度对齿轮传递效率有重要作用[7-9]。
综上所述,在考虑影响因素时,应将环境因素和能量传递过程中的影响因素都考虑在内,做出因素决策表,如表1所示,通过物联网平台对各个因素进行数据的采集,作为算法分析的初始数据。
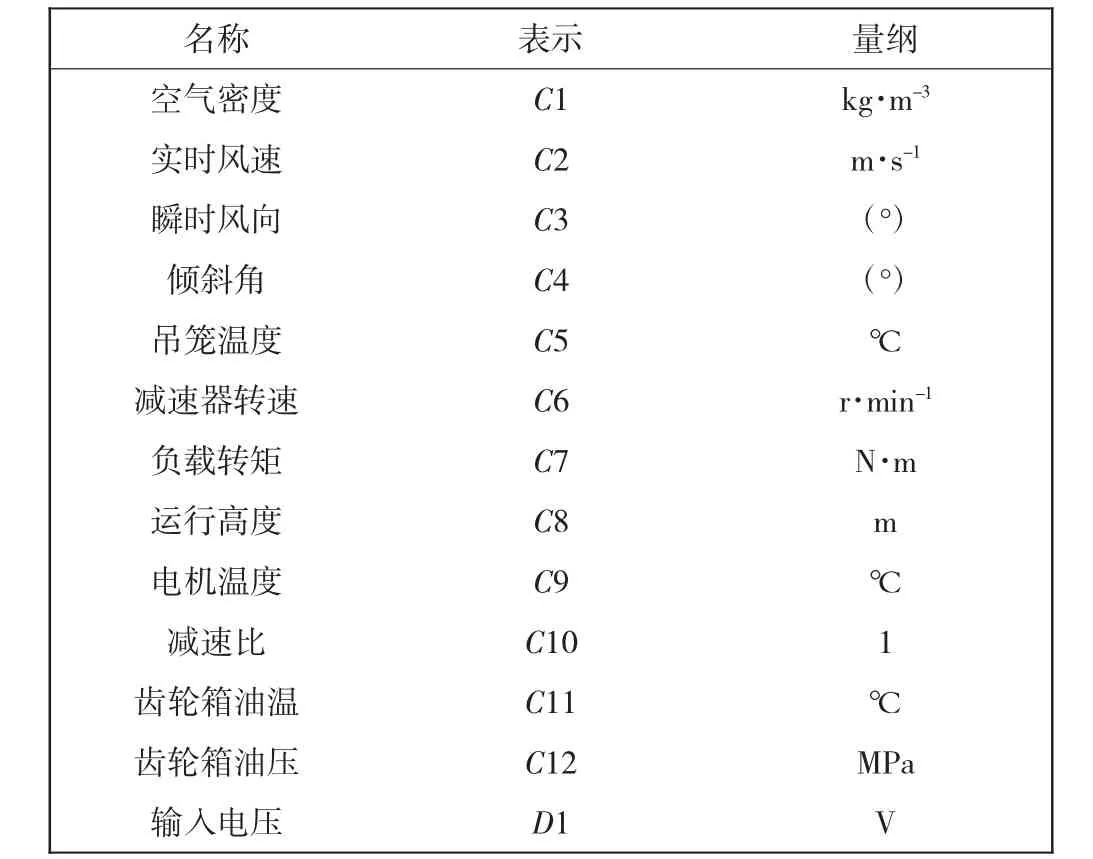
表1 因素决策表Tab.1 Factor decision table
2 基于RF算法的因素选择
由于输入电压受多因素影响,在进行回归分析时容易造成维数灾难、准确度下降、时间增加等问题,所以应该对多因素属性进行分类和因素选择。常用的分类选择算法有随机森林算法、朴素贝叶斯网络和鉴别分析分类器等。由于随机森林算法具有分类精度高、训练速度快、抗过拟合能力强、可处理高维度数据等优点,并且在训练完成后,能够检测属性间的影响及计算属性的重要性,所以本文选择随机森林算法。
2.1 随机森林(RF)定义及性质
随机森林算法是由Breiman L等[10-14]提出的,利用装袋(Bagging)算法优化的决策树模型,提升决策树的泛化能力。其利用自举法(bootstrap)和随机抽样法产生训练集和特征集,并构建决策树模型,通过投票方法计算出分类结果。
2.2 随机森林的建立
训练样本的生成是通过从训练集中随机且有放回地重复抽取K次,组成随机森林为f={h1,h2,…,hk}。从所有特征中随机抽m个特征子集构建决策树,并使用CART(分类与回归树)算法进行计算,其使用基尼指数(Gini,用G表示)挑选特征。设随机样本集D中第i类别样本占比为pi(i=1,2,…,m),且1,m表示类别总数,则D的基尼系数为:

假如某属性a将样本集D二元划分为D1、D2,则属性a的基尼系数为:
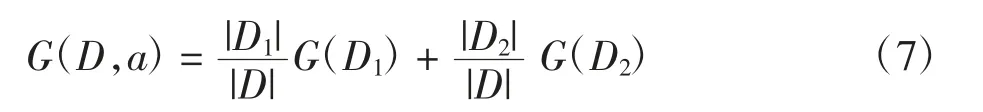
袋外数据(out-of-bag,OOB)指在生成训练集时,约有37%不会被抽到的样本。利用OOB对某个特征的重要性进行分析[15-17],设OOB数据集在第s棵树上的准确率为As,对任意变量U进行重要性分析,详细步骤为:
(1)重新随机排列训练集中变量U的值,得出新训练集NU,再次投入随机森林中,在决策树hs中OOB的分类准确率为AUs,s=1,2,…k;
(2)计算OOB在排列前后的分类准确率之差:
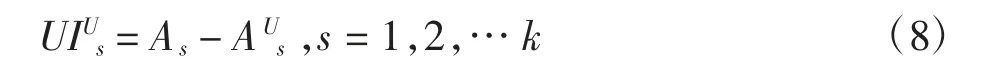
(3)变量U的重要性得分:

3 基于GA优化的SVM电压回归模型
本文通过随机森林算法对多因素进行选择后,再进行回归预测。支持向量机算法是最常用的回归方法,但传统参数确定方法还需要进行优化。本研究采用精度高、准确率好的遗传算法对参数进行优化。
3.1 支持向量机原理
支持向量机(SVM)通过求解最优分类超平面来确保划分样本的正确性,并使样本与超平面的误差最小,其计算常需要引入不敏感损失函数和核函数。本研究使用的支持向量机算法具体步骤[18-19]为:
(1)设已知训练集
式中:xi∈X=Rn,xi为特征向量;yi=Y[1,-1](i=1,2,…,l)。
(2)恰当选择核函数K(x,x')和惩罚因子C,构造和计算最优化问题
近年来,随着高校信息化水平逐步提高,智慧校园建设已成为高校建设发展的重要内容,面向学校校务管理及服务的各类信息系统逐渐建立并应用起来,这些独立的MIS系统在一定程度上解决了学校行政管理与服务方面的问题[3]。但随着业务数据的积累和各业务的不断变化,围绕学校主要业务(包括人事、科研、财务、学工、教务等)建设信息系统的高校信息化模式存在以下问题。
计算出最优解a*=(a1*,…,al*),式中:x为空间中的点;g为径向基半径。
(3)选择a*的一个正分量0 (4)构造决策函数 因为SVM回归的准确率和精度取决于惩罚因子C和径向基半径g的值,传统支持向量机是通过经验来寻找最优参数值的,准确度较低,本文利用遗传算法对传统支持向量机进行参数优化。 遗传算法(GA)主要用来寻找最优解,过程模拟了生物进化。计算的过程需要首先使用到计算机的编码方法,确定适应度函数;其次个体染色体通过随机生成初始种群,并计算个体的适应度值,根据生物进化原则,挑选出适应度好的个体;最后经过遗传算子选择出最优参数。利用GA优化SVM的参数C和g,基本步骤如图2所示。通过这些步骤可以找到最优的参数[20],通过参数优化使支持向量机的精度提高,结果达到最优。 图2 GA优化SVM参数的建模流程图Fig.2 Modeling flow chart of GA optimizing SVMparameter 在回归模型中,对预测的结果进行评价,常用RMSE、MAE、MAPE和R2这几个评价指标。其中,RMSE、MAE主要是对预测的稳定性进行评价,MAPE和R2是对预测的准确性进行评价。R2的数值越接近1,模型越准确;其它指标计算结果越小,回归模型越稳定、准确。 利用RF算法进行分类计算时,将12个因素变量作为输入量,输入电压作为输出量,参数设置为决策树个数200,特征属性用log2M+1计算,决策树迭代过程如图3所示,出袋错误量在决策树数量为12后趋于恒定值,说明RF算法具有较强的泛化能力。 图3 决策树迭代过程Fig.3 Iteration process of decision tree 利用OOB数据对输入量进行重要度计算,得到结果如图4所示,由图4可以得出各个因素的重要度值如表2所示。 图4 输入因素重要度分析Fig.4 Importance analysis of input factors 表2 重要度属性表Tab.2 Importance attribute table 根据表2中的重要度值可以得出:倾斜角、齿轮箱油温、瞬时风向、吊笼温度等为负值即干扰因素;减速比、齿轮箱油压由于数值较小可以忽略;因此,选取运行高度、减速器转速、负载转矩、实时风速、空气密度和电机温度这6个因素作为回归预测的样本数据。 用ROC曲线和AUC面积来评价分类的准确率,ROC曲线下方的面积即AUC面积,其面积越大,分类模型准确性越好。没有经过因素选择和经过因素选择的数据,通过SVM训练的ROC曲线对照如图5所示。由图5可以看出,经过因素选择之后,分类的准确率提高,说明因素选择是合理的。 图5 ROC曲线Fig.5 ROC curve 通过RF算法计算重要度值并进行因素选择后分类准确率升高,维数降低。因素选择后的样本约简集合如表3所示,此集合作为GA-SVM回归模型的样本数据。 表3 因素选择后的约简集合Tab.3 Reduction set after factor selection 对数据进行归一化处理,使用GA优化SVM的参数C和g,GA算法的参数设置为最大进化代数为300,交叉概率为0.4,变异概率为0.01,最大种群数量为40,代沟为0.9,惩罚因子C的变化范围为[0,100],径向基半径g的变化范围为[0,100],计算得到适应度曲线如图6所示。 图6 适应度曲线Fig.6 Fitness curve 由图6可以看出,终止迭代代数为150,进化代数在12代之后最佳适应度值达到稳定并有小幅波动,且与平均适应度的间距较小,说明收敛速度快,适应度较好。运行得到的最优参数C=3.565 3,g=0.040 3,并且适应度曲线的均方差MSE=0.001 518 1,说明参数计算的精确度较高。 SVM利用最优的C和g参数进行回归预测,结果如图7和图8所示,并对图7、图8中的数据进行回归分析,计算得到的评价指标值如表4所示。由表4可知,RMSE、MAE、MAPE数据较小,说明本文回归模型较准确;训练样本的R2为0.980 263,检测样本的R2为0.982 326,说明本文回归模型的预测正确性和稳定性很好。 表4 回归评价指标表Tab.4 Index table of regression evaluation 图7 训练样本的回归预测Fig.7 Regression prediction of training samples 图8 检测样本的回归预测Fig.8 Regression prediction of test samples 针对施工升降机供电电压有级调节带来的能耗浪费问题,将RF算法与GA-SVM算法相结合,提出RF-GA-SVM算法输入电压控制模型: (1)通过RF算法选择出运行高度、减速器转速、负载转矩、实时风速、空气密度和电机温度等6个重要度较高的因素,采用SVM得出ROC曲线和AUC面积,结果表明,因素选择后分类的准确率提高。 (2)采用GA算法对SVM进行优化,计算得出最优参数C为3.565 3,g为0.040 34,MSE为0.001 518 1。使用优化后的SVM对训练数据和测试数据进行回归预测,并对输入电压的预测值进行回归评价,检测样本的RMSE为1.493,MAE为0.899,MAPE为0.291%,R2为0.982,说明采用RF-GA-SVM算法进行输入电压的预测是准确、稳定的,将算法用于控制系统中可以有效控制输入电压。
3.2 遗传算法(GA)优化支持向量机(SVM)
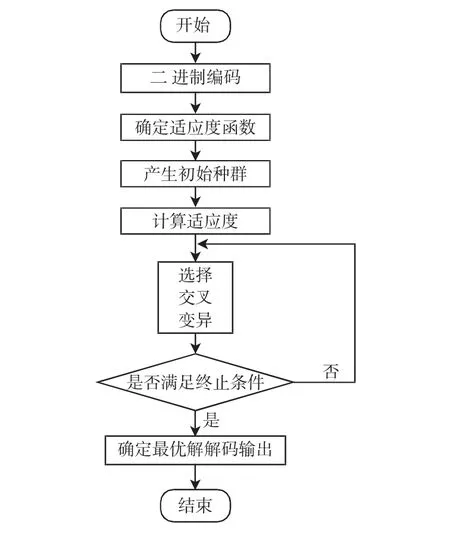
3.3 回归模型的评价指标
4 实例分析
4.1 因素选择
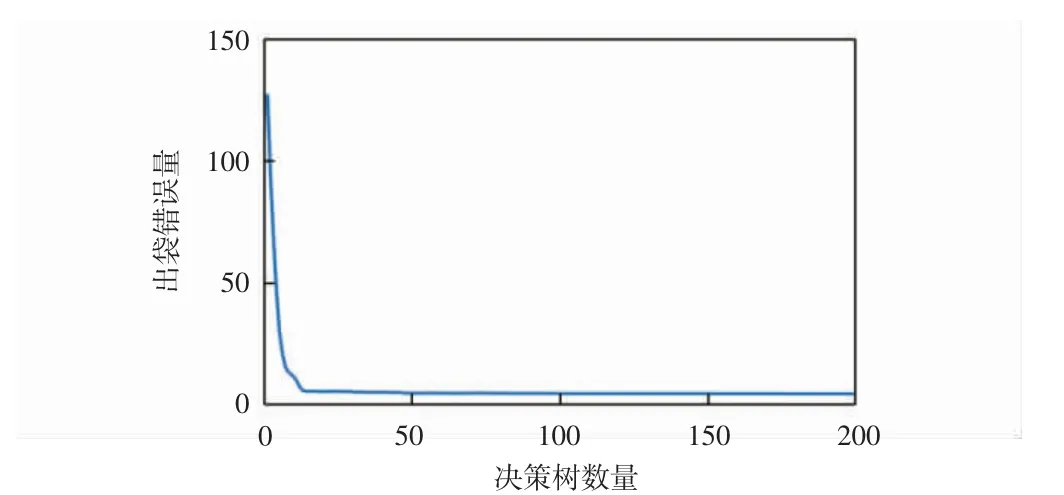

4.2 回归预测

5 结论
