数据驱动的卫星关键部件剩余寿命预测模型

刘大禹，徐二宝

（1. 中国东方红卫星股份有限公司，北京 100081； 2. 西安理工大学 机械与精密仪器工程学院，西安 710048）

0 引言

人造卫星载荷结构复杂、零部件繁多的特点给其健康管理带来了巨大的挑战。一旦某个关键零部件发生故障，将会引起连锁反应，甚至导致整个卫星服务中断。为了保证卫星在轨运行期间的高可靠性，减少意外故障的发生，对卫星及其载荷各子系统模块的健康状况进行预测成为一项极为重要的工作。

目前卫星的剩余寿命预测大多基于传统的可靠性和随机过程等统计学的方法，一般使用随机过程来描述设备的退化过程，用可靠性分布和参数估计等手段获得卫星零部件的故障概率和剩余寿命。然而，目前卫星逐渐向小型化和轻量化的趋势发展，且其精密程度越来越高，功能越来越强大，结构越来越复杂，影响其剩余寿命的因素具有多维、耦合等特点，因此越来越难以用精准的可靠性分布模型来描述卫星部件的退化和失效进程。

近年来，随着以物联网、大数据、人工智能为代表的新一代信息技术的蓬勃发展，传统的基于可靠性的预测方法正朝着更为直接、有效的基于数据驱动的方式转变。基于数据驱动的剩余使用寿命（remaining useful life, RUL）预测方法主要利用深度学习技术，具有较强的自适应特征提取能力，无需专业的统计学知识和精准的机理模型，完全依赖历史数据以及实时状态监测数据对设备的RUL进行预测，预测精度较高、普适性较强。事实上，随着健康管理技术的应用和发展，某些卫星已经建立了完善的实时在轨数据采集系统，并积累了一定数量的历史数据，为实施基于数据的预测提供了重要的支撑。

通过对现有研究成果的梳理发现，目前的卫星RUL 预测模型大多是基于卫星本身的遥测数据，并使用卷积神经网络（convolutional neural networks,CNN）或长短时记忆网络（long short-term memory,LSTM）等深度学习技术来构建的，普遍缺乏对部件周边环境类以及地面统计类等数据信息的考虑，导致预测精度不高。为了更精准预测卫星关键零部件的RUL，同时解决CNN 和LSTM 技术存在的时序数据提取能力不足以及模型训练速度过慢的问题，本文选用门控循环单元（gated recurrent unit,GRU）网络对卫星关键零部件的RUL 进行预测；而且在基于GRU 构建预测模型时除卫星遥测数据之外，将热噪声温度等在轨环境类数据以及通信质量等地面统计类数据也考虑进去，并使用CNN 与GRU 融合的方法来改善GRU 网络模型提取特征能力不足的问题。

1 GRU 理论基础

与传统的前馈神经网络不同，GRU 网络能同时处理当前和前序时间的数据，解决了传统神经网络难以有效处理时序类型数据的问题。GRU 网络由输入单元、输出单元和隐藏单元3 部分组成，其模型架构如图1 所示，其中，x、s和o分别为位置的输入数据、隐藏单元输出和输出单元输出。

图1 GRU 模型架构Fig. 1 Architecture of the GRU model

从其模型架构可以发现，GRU 处理时序数据时，序列中每个当前位置的输出值不仅依赖于当前位置的输入x，还依赖于前序位置隐藏单元的输出s，以此来实现对前序位置信息的记忆。GRU 的隐藏单元是一个比较复杂的门限结构，如图2 所示，每个隐藏单元包含更新门和重置门2 个门控。

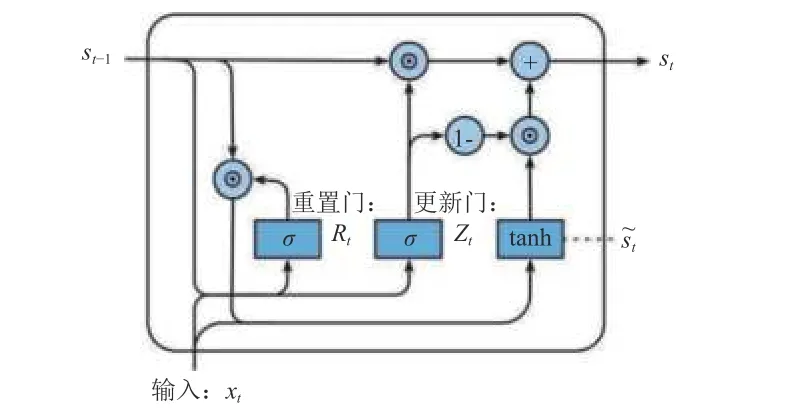
图2 GRU 隐藏单元的门限结构Fig. 2 Threshold structure of the hidden cell of the GRU model

更新门控制着序列中前序位置信息保留到当前位置的程度Z，值越大表示在当前位置中保留了越多的前序位置信息，更新门Z的计算表达式为

式中：(·)为Sigmoid 激活函数；为更新门对输入向量的权重；为更新门对前序单元输出的权重。

重置门控制着当前位置状态与前序位置信息结合的程度，R值越小说明忽略的信息越多，重置门R的计算表达式为

式(3)和式(4)中：为隐藏单元输出时对输入向量的权重；为隐藏单元输出时对前序单元输出的权重。

式(1)～式(4)中的、、、、、均为可训练的参数矩阵，在得到隐藏单元输出s后，经过全连接网络，即可得到当前位置的输出o。

2 数据驱动的卫星RUL 预测模型构建

卫星健康状态数据通常具有非线性相关、时序性强及退化过程复杂的特点，增加了后续时序特征提取及数据趋势预测的难度，导致在对卫星RUL进行预测时，使用一般的机器学习方法或单一的深度学习方法的预测效果无法满足应用要求。相比于RNN、LSTM 等常见的处理时序型数据的方法，GRU 可通过引入门控机制很好地解决模型训练时容易梯度消失的问题，并且能以更少的训练参数达到较佳的预测效果，因此本文选用GRU 网络进行RUL 预测；同时考虑到CNN 在从原始数据中提取显著特征时往往优于其他神经网络，结合CNN 和GRU 的网络结构优势，使用CNN 进行特征提取，将CNN 输出结果作为GRU 的输入，建立CNN 与GRU相融合的RUL 预测方法。相比原始输入，CNN 能够对更多关键信息进行编码，压缩序列的长度，增强后续GRU 捕获时间信息的能力；同时，模型的输入数据不仅包含传统的卫星遥测类数据，还添加了卫星在轨环境类数据，旨在提高卫星RUL 的预测精度。综上所述，本文提出的基于CNN-GRU 的卫星RUL 预测模型如图3 所示。

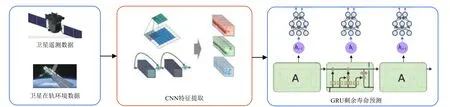
图3 基于CNN-GRU 的卫星RUL 预测模型示意Fig. 3 Schematic model for predicting RUL of satellite based on CNN-GRU

3 算例分析

为验证所构建模型的有效性，本文以某型号卫星的天线转发器这一通信系统关键部件作为具体研究对象，进行其RUL 预测。

影响天线转发器性能的主要参数为G/T（接收系统品质因数）、SFD（饱和通量密度）和EIRP（有效全向辐射功率），均与天线增益在轨监测参数息息相关。用于数据驱动的原始数据集除了包含天线增益在轨监测参数外，还要包括从地面站遥测历史数据库中检索出的遥测数据传输帧率、遥测误码率、信噪比、丢帧率、数据帧时延等反映通信质量的统计类参数数据，以及天线热噪声数据。卫星温度测点相对较少，因此将星间链路天线主反射器和锁紧/释放装置的温度等价为天线热噪声参数，用以反映天线在轨环境。最终把这些参数数据一并输入到模型中，将60%的数据作为训练集，20%的数据作为验证集，剩余20%的数据作为测试集，分别建立GRU 回归模型和CNN-GRU 模型对天线转发器的RUL 进行预测。

两模型均选择平均绝对误差（MAE）作为损失函数，选择tanh 激活函数，设置最大迭代步数为500。为防止模型出现过拟合情况，在模型中加入早停法，以获得更好的泛化性能。GRU 回归模型训练过程的迭代损失如图4(a)所示，迭代172 次后，模型在验证集上的表现开始下降，此时须停止训练。在模型验证环节，预测值与真实值的比对如图4(b)所示。图中的真实值是根据卫星发射时间及退役时间分阶段进行线性处理得到的，真实值（红线）中的拐点是天线转发器首次发生参数数据异常的运行时间点。

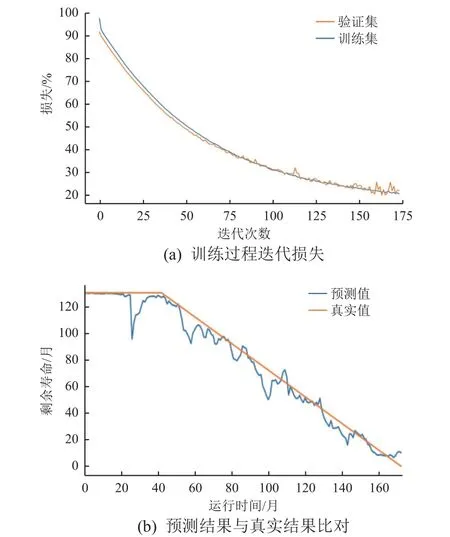
图4 基于GRU 的天线转发器RUL 预测模型Fig. 4 The prediction model for RUL of the antenna transponder based on GRU

通常使用MAE、均方根误差（RMSE）、决定系数（）等评价指标来衡量模型在训练集、验证集和测试集上的预测精度。MAE、RMSE 这2 项指标越小代表模型的预测精度越高；的范围为[0, 1]，其值越大表示模型拟合效果越好。GRU 模型的RUL预测结果评价如表1 所示。结果表明，该模型相比传统的LSTM 模型，预测准确度提高了近70%，预测速度提高了近10%，能更好满足大规模时序数据的预测需求。

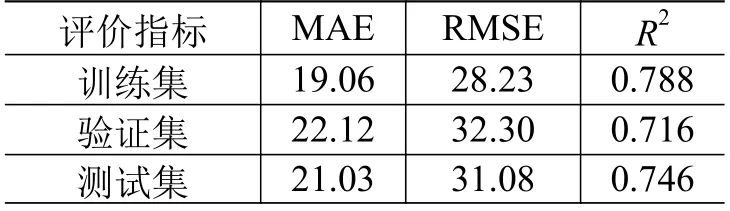
表1 GRU 模型RUL 预测结果评价Table 1 Evaluation of RUL prediction results based on GRU model

CNN-GRU 模型训练过程的迭代损失如图5(a)所示，迭代198 次后，模型在验证集上的表现开始下降，此时须停止训练。在模型验证环节，预测值与真实值的比对如图5(b)所示。相较于图4(b)可以直观地看出，CNN-GRU 模型的预测结果明显更接近真实值。

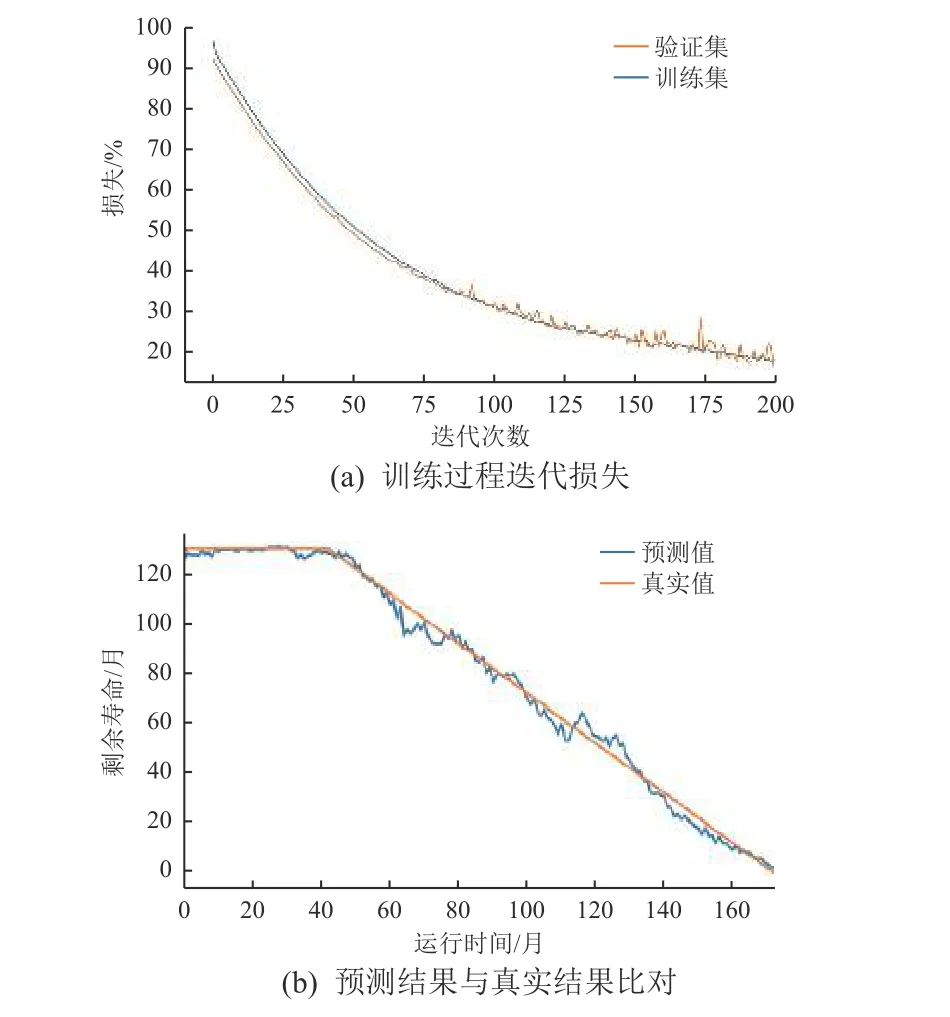
图5 基于CNN-GRU 的天线转发器RUL 预测模型Fig. 5 The model for predicting RUL of the antennatransponder based on CNN-GRU

CNN-GRU 模型在训练集、验证集及测试集上的RUL 预测结果评价如表2 所示。

表2 CNN-GRU 模型RUL 预测结果评价Table 2 Evaluation of RUL prediction results based on CNNGRU model

对比表1 和表2 可见，CNN-GRU模型RUL 预测结果的各项评价指标均较单纯GRU模型的有明显提升，说明CNN-GRU 模型的预测结果更接近真实值，验证了本文所提出的基于CNN-GRU 的卫星关键部件RUL 预测模型具有更高的预测精度。

4 结束语

本文构建了基于数据驱动的卫星关键部件剩余寿命预测模型，并将CNN 和GRU 相融合进一步优化模型。选取某型号卫星的天线转发器的数据传输质量类参数以及天线热噪声温度参数作为原始数据集，采用单纯的GRU 模型和CNN-GRU 融合模型进行RUL 预测。对两模型RUL 预测结果的评价对比，验证了相较于单纯的GRU 模型，本文提出的CNN-GRU 融合模型可充分发挥CNN 在特征提取能力方面以及GRU 在时间序列预测方面的优势，能更快速、精准地对卫星关键零部件的剩余寿命进行预测。