变系数耦合抛物方程边界能控性的必要条件

谢伟松， 张青青

(天津大学 数学学院, 天津 300350)

近年来，关于耦合抛物型偏微分方程能控性的研究已成为一项具有挑战性的工作，备受众多学者的关注[1-7].这些控制问题一般分为标量抛物型问题和非标量抛物型问题.

对于标量抛物型问题，能控性的研究已经相对成熟.例如，Fattorini等[8]用矩量法证明了一维热方程的零边界能控性的第一个结论.对于一般抛物型方程，Lebeau等[9]和Fursikov等[10]通过局部Carlmeman估计证明了其零能控性.结合Caroline等[11]的不动点方法，Enrique等[12]对于具有全局Lipschitz非线性的半线性热方程、甚至非线性方程以超线性方式增长但增长速度缓慢时，也得到了类似的结果.

对于非标量抛物型问题，研究工作大多集中在系统的内部能控性上，并且得到了系统能控的充分必要条件或者充分条件.Khodja等[13]主要研究了非自治抛物线性系统内部近似能控的一个充要条件.Manuel等[14]分析了m-方程线性耦合抛物系统在施加唯一分布式控制时的能控性.Dupaix等[15]证明了卡尔曼秩条件是获得n-耦合抛物型方程相对于迹精确能控性的充分条件而不是必要条件.杜润梅[16]考虑了两类耦合退化系统，证明了问题的零能控性，并利用Manuel等[17]的方法研究了“双”线性耦合退化系统的零能控性.Enrique等[18]研究了一类线性和半线性不可对角化抛物型偏微分方程组的内部能控性.Zhu等[19]通过共轭问题构造控制，证明了一类由耦合退化方程控制的系统是近似能控的.Du[20]考虑了一类带梯度项的耦合退化抛物型方程的近似能控性，并利用伴随方程的唯一延拓证明了方程的近似能控性.

关于非标量抛物系统边界零能控性的研究结果很少.Enrique等[21]给出了常系数非标量线性抛物型2×2系统(n×n系统[22])的零能控性的充分必要条件.Piermarco等[23]考虑了两个耦合一维退化抛物方程系统的零能控性，推广了在一维域[24-25]中得到的Carleman估计，恢复了与Manuel等[26]类似的能控性结果.Alabau-Boussouira等[27]考虑了n维情况，给出了一些充分条件和适当的几何条件.Molina[28]研究了具有控制的非等熵情况下，可压缩Navier-Stokes方程在有界域Ω上的边界能控性.

本文考虑拉普拉斯算子系数随时间变化的非标量抛物型方程边界能控性的必要条件.

本文用到的一些空间和符号表示的含义如下.

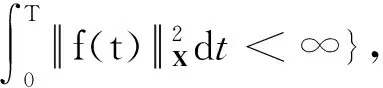
使得L2(0,T;X)是一个Banach空间[29].

当不引起混淆时L2(0,T;X)也可以简写为L2(X).由Magenes等[30]知，当X=Hm(a,b)时，L2(0,T;X)是一个Hilbert空间.

定义有界算子空间如下：L(R2;R2)={A:R2→R2,A是有界线性算子}，也可以简单记作L(R2)，L(R;R2)={A:R→R2,A是有界线性算子}.

1 问题和主要结果

固定T>0，考虑以下线性变系数方程

(1)

式中:A∈L(R2)和B∈L(R;R2)已知，y0∈H-1(0,1)2，v∈L2(0,T)是控制函数，y=(y1,y2)*是状态变量，a(t)>0且a(t)∈L2(0,T).

方程(1)具有适定性，并且对应的解连续的依赖于y0和v.对于任意的y0∈H-1(0,1)2，存在一个控制v∈L2(0,T)，使得其解满足:

y(x,T)=0且y(x,T)∈H-1(0,1)2

(2)

则称方程(1)在T>0是零能控的.

本文研究方程(1)的边界能控性，并且只将控制作用于边界的一部分.主要研究结果如下：

命题1若方程(1)在T>0是零能控的，那么卡尔曼秩条件

rank[B|AB]=2

(3)

成立.

证明若B=0，显然方程(1)在T>0不是零能控的，故只需考虑B≠0的情况.

用反证法证明.假设rank[B|AB]=1，即存在α∈R使得AB=αB.

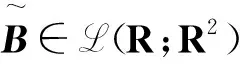
那么

因此

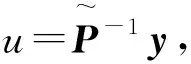
等价于

由于u的第二个组成部分是独立于v的，所以这个方程显然不是零能控的.这与假设方程(1)在T>0是零能控的相矛盾.因此，卡尔曼秩条件是方程(1)在T>0是零能控的一个必要条件.

定理1设A∈L(R2)和B∈L(R;R2)，A的特征值为μ1和μ2.若方程(1)在T>0是零能控的，那么对于任意k,j∈N且k≠j，存在t0∈(0,T]使得

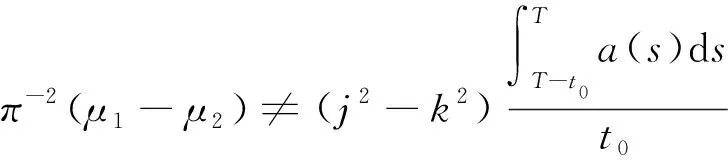
(4)

基于抛物型耦合方程的边界能控性，利用与Fattorini等[8]类似的方法和可观性不等式，容易证明定理1.

接下来给出方程(1)的弱解的存在唯一性以及方程(1)在T>0是零能控的等价命题.

2 观测不等式

为定理1的证明提供一个等价命题，即方程(1)的零能控性等价于其对应的可观测性不等式.

考虑线性向后演化方程

(5)

式中：g∈L2(0,T;L2(0,1)2).对于任意的g∈L2(0,T;L2(0,1)2)，方程(5)的解满足:

命题2设y0∈H-1(0,1)2，v∈L2(0,T)且y∈L2(0,T;L2(0,1)2).对于任意的g∈L2(0,T;L2(0,1)2)，方程(1)存在唯一弱解

y∈L2(0,T;L2(0,1)2)∩C([0,T];H-1(0,1)2)

且满足：

(6)

式中：z是方程(5)的解.

证明对于任意的g∈L2(0,T;L2(0,1)2)有

∬Ωy*gdxdt=

∬Ωy*(-zt-a(t)zxx-A*z)dxdt=

-∬Ωy*ztdxdt-∬Ωy*(a(t)zxx)dxdt-

∬Ωy*(A*z)dxdt

又

∬Ωy*(a(t)zxx)dxdt=

那么

-∬Ωy*ztdxdt-∬Ωy*(a(t)zxx)dxdt=

∬Ω(Ay)*zdxdt

由于A*是A的伴随矩阵，那么

因此式(6)成立.

又方程(5)的解满足：

且

由正则性可知，对于任意给定的y0∈H-1(0,1)2和v∈L2(0,T)，存在满足式(6)的唯一弱解.

考虑方程(1)的伴随方程

(7)

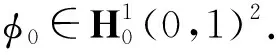
命题3下面两个性质等价

1) 对于任意的y0∈H-1(0,1)2，存在常数C>0和一个控制v∈L2(0,T)，使得

(8)

且状态变量满足式(2).

(9)

成立.

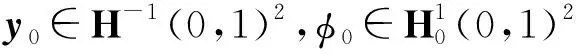
a(t)B*φx(0,t)v(t)

因此可以得到

〈y(x,t),φ(x,t)〉-〈y0,φ(x,0)〉=

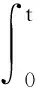
(10)

由1)推导2).在式(10)中令t=T，则

〈y(x,T),φ(x,T)〉-〈y0,φ(x,0)〉=

又在H-1(0,1)2中y(x,T)=0，因此

由y0和φ(x,0)的任意性可以得出

由2)可以推导1).固定y0∈H-1(0,1)2，构造一族适当的最优控制问题.对于任意的ε>0，考虑相应于方程(1)的最优控制问题

其中：y∈L2(0,T;L2(0,1)2)是与y0和v有关的状态变量.

利用变分法不难得出该控制问题有一个精确解vε∈L2(0,T)，且

vε(t)=-B*a(t)φε,x(0,t)

以及最优系统的伴随解

令t=T，将φε(x,T)和vε(T)代入式(10)中，则

由拉普拉斯算子的自伴随性，可得

因此

(11)

这个估计使得能够得到一个L2(0,T)中的子序列满足：

vε⇀v

yε(x,t)⇀y(x,t)

以及在H-1(0,1)2有

yε(x,T)⇀y(x,T)

在式(11)两边令ε→∞，则

因此，存在一个控制v满足式(8)且y(x,T)=0.

3 定理1的证明

定理1的详细证明过程如下.

证明记P=[B|AB]，则

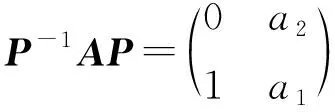
其中a1和a2是矩阵A的特征多项式qA(μ)=μ2-a1μ-a2的系数.

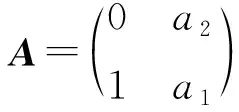
由命题3知，方程(1)的零能控性等价于其伴随方程(7)的解满足的可观测不等式.为了处理这个不等式，可以将原来的控制问题重新表述为如下问题：

设M(t)是常微分方程χt=Aχ的基解矩阵，ψ和ξ满足：

y=M(t)ψ和φ=M(t)*ξ

将y=M(t)ψ代入方程(1)，则ψ满足:

由于M(t)是χt=Aχ的基解矩阵，则

(12)

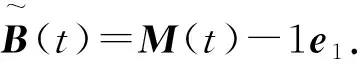
(13)

由于y=M(t)ψ，则方程(1)在T>0是零能控的等价于方程(12)在T>0是零能控的.因此，方程(1)在T>0是零能控的也等价于观测不等式

(14)

由分离变量法可以得到，方程(13)的解为

(15)

式中：{λj:λj=j2π2}j≤1为狄利克雷拉普拉斯矩阵在(0,1)上的特征值序列，aj和bj是ξ0分量的傅里叶系数.

将t=0代入式(15)中并且取范数，则有

记

情况1：A有两个相同的实特征值，显然成立.

情况2：A有两个不同的实特征值.

因此，有

和

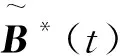
(16)

对于式(16)的右侧，有

因此，式(16)等价于

(17)

并且式(16)和式(17)是等价的.

不难证明若式(17)成立，则式(16)成立.下面证明当式(16)成立时，式(17)也成立.

由于

和

则

因此

故式(17)成立.

用反证法证明式(4)成立.假设存在j0,k0∈N且j0≠k0，对于任意的t∈(0,T]使得

成立.

设

式(17)的左侧满足:

式(17)的右侧满足:

由于

则

矛盾.

情况3：A有一对共轭的复特征值.

μ1=α+iβ和μ2=α-iβ

因此

M(t)=

(18)

对于式(18)的右侧，有

e-αt∂xξ2(0,t)a(t)cosβt|2dt=

类似式(16)和式(17)等价性的证明，不难得到式(18)等价于

(19)

其中

cj=aj+ibj和dj=aj-ibj.

用反证法证明式(4)成立.假设存在j0,k0∈N且j0≠k0，对于任意的t∈(0,T]使得

成立. 设

式(19)的左侧满足：

式(19)的右侧满足I=0，矛盾.