基于Kalman滤波的ARIMA-NAR神经网络模型在深基坑沉降监测中的应用

牛全福, 李月锋, 张 曼, 傅建凯, 马亚娜

(1. 兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2. 甘肃省应急测绘工程研究中心, 甘肃 兰州 730050; 3. 甘肃土木工程科学研究院有限公司, 甘肃 兰州 730050)

近年来，随着我国社会经济的快速发展，城镇化建设深入推进，建设用地日趋紧张，建设趋向高层、超高层的纵深发展，深基坑工程在城建中的安全施工显得越来越重要.近年来与基坑相关的工程事故频发[1-2],尤其在以湿陷性黄土为主的西北地区，深基坑工程在雨水较多的季节易发生变形甚至失稳现象.因此，进行基坑变形监测，掌握其变形状态，进而对未来的变形趋势做出预测对基坑工程安全开挖施工具有重要意义.

深基坑变形监测通常为长期的形变观测，并依据适宜的模型建模预测其变形趋势来指导安全施工.常用的数学模型有：回归分析模型[3]、灰色理论模型[4-6]、支持向量机(SVM)模型[7- 9]、时间序列模型[10-12]以及人工神经网络模型[13- 15]等.但是，单一模型虽有一定的趋势预测精度，但仍存预测残差随着期数增加而增大的问题[16], 因此，综合两种或两种以上模型优点的组合模型逐渐出现并应用到基坑变形预测中[17- 19]，方苏阳[20]等将时间序列模型与BP神经网络模型组合运用于地表沉降预测，取得了较好效果；王磊[21]等将ARMA模型与BP神经网络模型结合应用于基坑监测预测研究，得出其拟合精度要优于单一时间序列模型的精度的结论.

然而，为使深基坑监测预测能更加有效指导施工，除了选择较适宜的模型外，观测数据质量也制约着监测预测的精度.本文以兰州某深基坑施工监测项目为例，尝试一种基于Kalman滤波的ARIMA-NAR模型，探讨监测数据去噪情况下的组合模型监测预测精度，为本项目的安全施工提供指导.

1 基于Kalman滤波的ARIMA-NAR神经网络模型基本原理

1.1 Kalman滤波

由于监测数据不可避免的存在噪声，因此，本研究利用卡尔曼 (Kalman) 滤波对监测数据进行去噪处理.Kalman滤波基于最小二乘法法则[16]，采用前一刻的估计值和当前时刻的观测值，经过卡尔曼增益作用，实现对当前状态的最优化预测估计[22].

卡尔曼滤波数学模型由状态方程和观测方程两部分组成，离散化形式为

其中:Xk表示状态向量；Φk,k-1表示状态转移矩阵；Lk表示观测值向量；Ak表示设计矩阵；Wk和ek表示均值为零且相互独立的正态白噪声.利用Kalman滤波计算的预测状态向量为

(3)

计算新的状态估值为

(4)

1.2 ARIMA模型

差分自回归移动平均(auto regressive integrated moving average, ARIMA)模型[23]是将预测对象随时间(或空间)推移而形成的数据序列视为一个随机序列，然后用一个数学模型进行近似描述的模型.一旦这个模型的结构和参数确定后，就可以由这个序列的过去值及当前值对未来值进行预测.使用ARIMA模型进行建模，通常包括平稳性检验、平稳化处理、模型结构确定、参数估计和模型检验等过程[24].

ARIMA(p,d,q)模型一般表达式为

(5)

其中:hi为自回归项,i=1,2,…,p;p为自回归阶数；θi(i=1,2,…,q)为移动平均项，q为移动平均阶数；Δdyi为d阶平稳后的时间序列；ut为服从独立正态分布N(0,σ2)的白噪声序列.

1.3 NAR神经网络模型

非线性自回归模型(nonlinear auto regressive models，NAR)是基于时间序列的动态神经网络模型，由输入层、隐含层、输出层和滞后层四部分所组成.该模型每一时刻的输出是由当前时刻以前系统的动态结果综合拟合而得，具有反馈和记忆的功能[25].NAR神经网络模型表达式为

yn=G(yn-1,…,yn-k,xn,…,xn-1)

(6)

式中:x为模型输入;y为模型输出;n为离散时间;G为非线性函数.由于本研究的监测数据为时间序列，在模型的输入为未知情况下，对实测数据进行逼近计算时，NAR神经网络模型可改写为

yn=F(yn-1,…,yn-k)+kεn

(7)

式中:F为非线性函数;k为常数;εn为服从高斯分布的随机变量.

1.4 预测方法

基于Kalman滤波的ARIMA-NAR预测模型进行基坑监测预测工作流程如下：首先，将监测数据通过Kalman滤波算法剔除原始数据中的噪声；其次，利用ARIMA模型提取出滤波数据的趋势项，获取残差序列；最后，利用NAR神经网络模型对残差序列进行预测，获得最终的预测结果.具体流程如图1.

图1 技术流程Fig.1 Technical flowchart

2 工程实例分析

2.1 工程简介

兰州市某深基坑监测项目，场地东西向长约390 m，南北向宽约232 m，基坑深度为23.75 m，地下水位为3.7 m.钻探揭示场地土层主要为：填土层、粉土或粉质粘土层、卵石层以及砂岩层等.从2016年11月以来，对该基坑已连续观测了53期支护桩的沉降数据.为及时、安全指导基坑开挖施工，本项目一项重要是利用历史观测数据对有明显沉降的观测点进行监测预测工作.

2.2 随机噪声滤除

本试验选取兰州市某深基坑工程中ZJ52号监测点为研究对象，共观测了53期沉降数据.为便于验证，试验中将观测数据分为两部分，即前45期数据用于模型的建立，后8期数据用于预测结果验证.模型建立前的Kalman滤波去噪主要通过Matlab编程进行处理.对前45期监测数据进行Kalman滤波，从ZJ52监测点去噪前后的对比(图2)可以看出，原始监测数据在第12、20、21期出现明显跳变(噪声)，经Kalman滤波后的趋势线基本趋于光滑，且更加接近实际观测值，有效剔除了原始监测数据中的噪声(随机误差).

图2 滤波前后趋势对比Fig.2 Trend comparison pre- and post filtering

2.3 ARIMA模型预测

1) 平稳性检验

表1是对滤波后的时间序列进行ADF检验计算结果.可以看出，滤波序列在显著性水平0.01条件下的T统计量值小于-2.08，滤波序列接受存在一个单位根的原假设，表明滤波后序列为非平稳序列；一阶差分后的ADF检验表明，在显著水平0.01条件下的T统计量值小于-3.33，一阶差分序列拒绝存在一个单位根的原假设，且一阶差分后的自相关图(图3)较快减小至虚线以内，说明经过一阶差分后的序列已为平稳序列，可以为以后建模使用.

表1 滤波后ADF检验

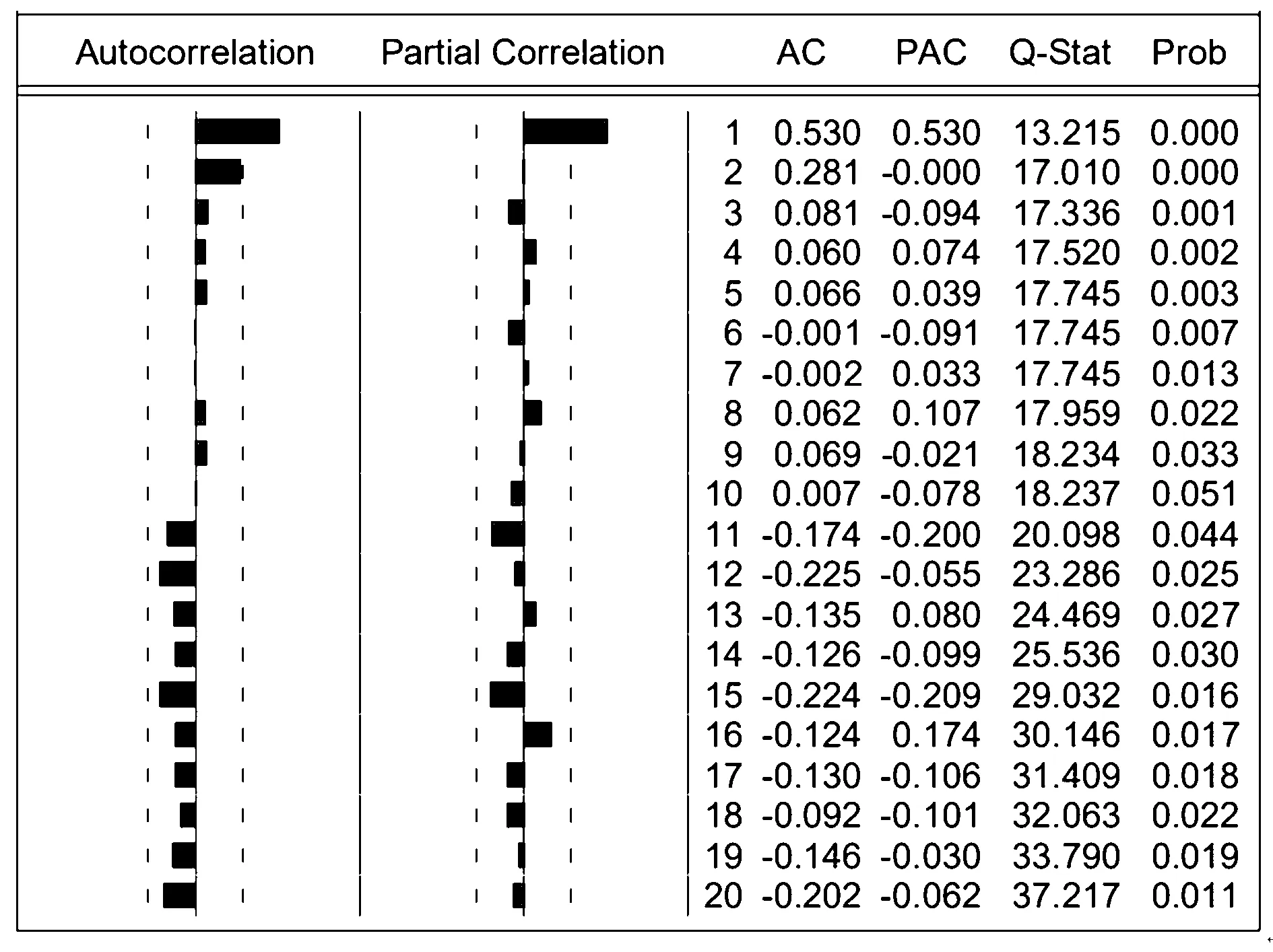
图3 差分序列相关图Fig.3 Correlation diagram of difference sequence

2) 模型建立与预测

根据残差序列的自相关图和偏自相关图(图3)以及不同的滞后阶数下的自相关数、偏自相关数所在的置信区间，确定的时间序列模型结构为ARIMA模型，根据项目监测中前45期滤波后的数据构建的模型，然后对项目监测的后8期数据进行预测(图4).结果显示，预测值的前2期较接近于实测值，随着预测期数的增加，预测结果残差也逐渐增大，残差的累计也随之增大，预测结果逐渐偏离实测值，预测结果并不理想.

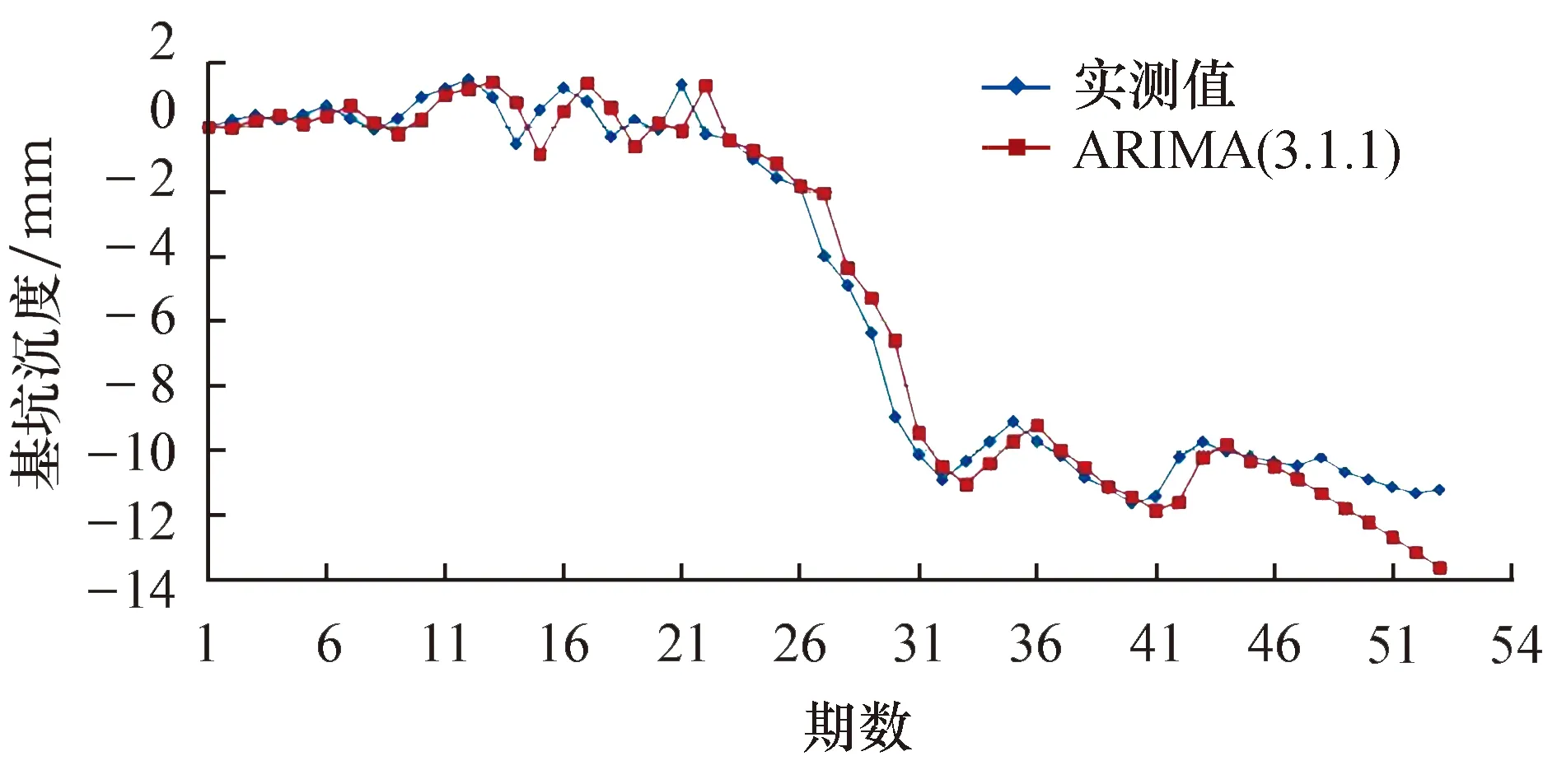
图4 ARIMA(3.1.1)预测曲线Fig.4 ARIMA(3.1.1) prediction curve

2.4 NAR神经网络模型

NAR神经网络建立中，隐藏神经元的个数过多会增加神经网络的训练时间和迭代计算次数，会出现过拟合现象，神经元个数过少会出现拟合效果差、样本识别率低等问题.因此，通过多次计算(表2)，本文确定隐藏神经元个数为6个.

表2 不同神经元个数下的MAE、RMSE、R2值

将项目监测的前45期数据(训练集31期、验证集7期、测试集7期，滞后阶数为2，隐藏神经元个数为6)进行训练.统计结果发现(图5)，训练数据和验证数据拟合优度均在0.996以上，测试集拟合优度为0.989 67，接近1；残差自相关的阶数(除0阶外)均位于95%置信区间内.基于模型上述参数，运用Matlab编程工具，对项目监测中的后8期数据进行预测(图5).结果发现，验证数据中，前4期与实测数据较接近，而后4期随着期数的增加，逐渐偏离了实测结果.

图5 NAR预测曲线Fig.5 Prediction curve of NAR

2.5 ARIMA-NAR组合模型预测

首先将原监测数据经过Kalman处理，获得去噪后的时间序列数据；其次，利用ARIMA模型提取去噪后时间序列数据的趋势项，得到残差序列数据；然后，利用残差序列数据经NAR神经网络进行建模，并对项目监测的后8期数据进行预测计算；最后，将预测结果与ARIMA、NAR神经网络模型的预测结果进行对比(表3和表4).

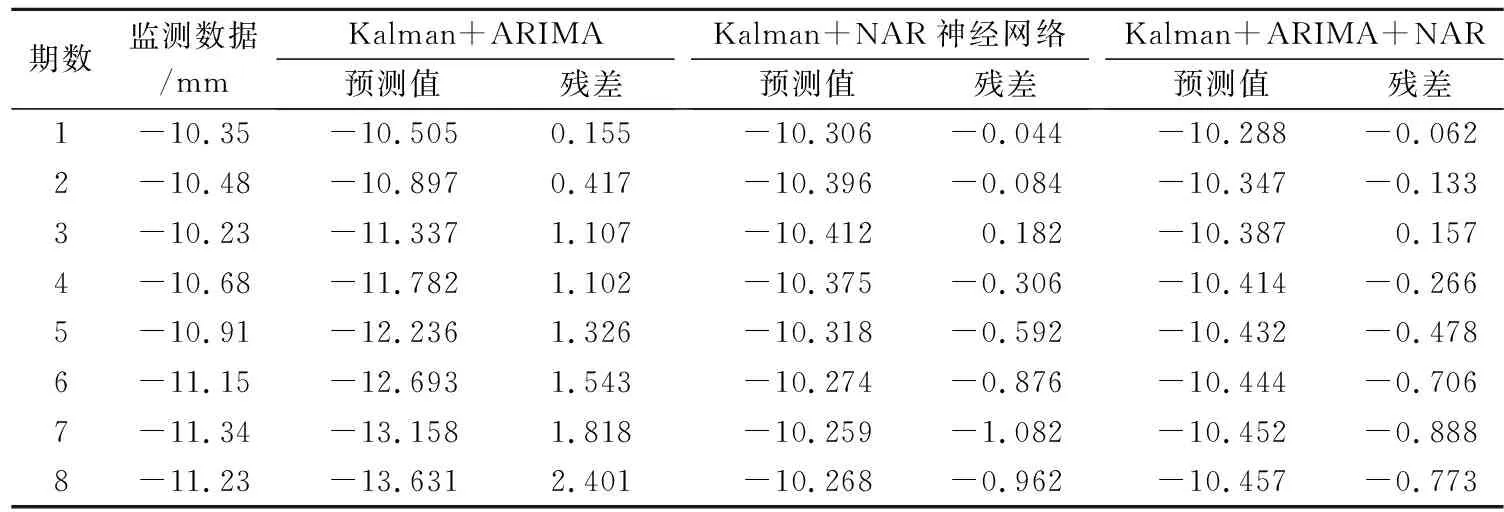
表3 三种模型预测结果对比

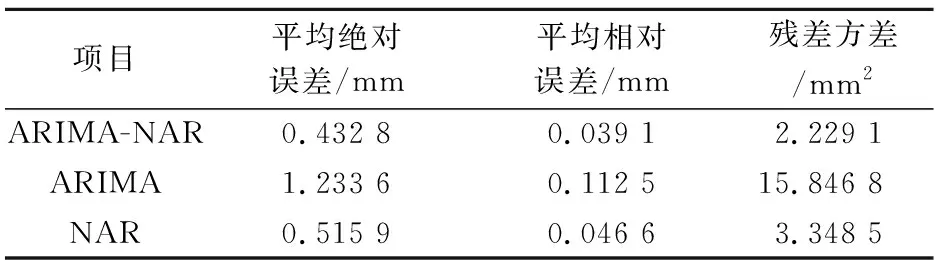
表4 三种模型预测精度对比

由表3和表4可知，基于Kalman滤波的ARIMA-NAR组合模型的平均绝对误差、平均相对误差和残差方差分别为0.43、0.04、2.23 mm，其预测结果均优于单一的ARIMA和NAR神经网络模型的预测结果.能对深基坑监测项目短期内的变形进行有效预测.

3 结论

基坑变形监测预测在现代城市建设安全施工中显得越来越重要.本文以兰州市某深基坑监测中具有明显沉降的ZJ52点为例，采取基于Kalnman去噪的ARIMA-NAR神经网络组合模型进行监测预测分析，取得了如下结论：

1) 由于监测数据不可避免地存在噪声，故将ZJ52点的53期沉降监测数据在模型建立前经Kalman滤波处理，结果显示原监测数据在第12、20、21期出现明显跳变(噪声)，经去噪后的趋势线基本趋于光滑、较接近于实际观测值，有效剔除了原始监测数据中的随机误差.

2) 将去噪后的时间序列基于ARIMA模型进行后8期预测，随着预测期数的增加，预测结果随着残差的累积逐渐偏离实测值；利用NAR神经网络模型预测，其结果较ARIMA较好，但仍存在随着期数的增加，与实测结果相偏离的问题；利用经过Kalman滤波的ARIMA-NAR组合模型进行预测发现，其平均绝对误差、平均相对误差和残差方差分别为0.43、0.04、2.23 mm，预测结果均优于单一的ARIMA和NAR神经网络模型的预测结果.

3) 本文基于监测数据存在不可避免的噪声及单一模型存在的缺陷，仅采取基于Kalman滤波的ARIMA-NAR神经网络组合模型、利用不同算法的优势进行基坑沉降监测、预测应用分析，对模型本身带来的预测质量较少探讨，因此，下一步将在算法自身的缺陷方面进行探讨，以期对深基坑监测预测提供借鉴.