模型纵然千百变，等距定心是关键*

福建省福清第一中学 (350300) 林琳琳

福建省福清市教师进修学校 (350300) 林新建

多面体外接球问题一直是数学高考的热点，此类问题由于模型多变，难度较大，要求学生有较强的直观感知和空间想象的能力，考生往往难以完美作答.其实，解决此类问题的关键在于球心位置的确定，考生若能直观问题的本质，依据球心到多面体各个顶点的距离相等，以及球心在各个面上的投影到面上各个顶点的距离也相等，则不难确定出球心的位置，问题也就不难获得解决.本文给出确定球心位置的四种策略，供借鉴.

1.依循定义，等距定心

依循多面体外接球的定义，循序找出与各顶点距离相等的点，该点即为多面体外接球的球心，问题随之获得解决.

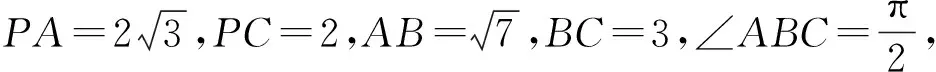
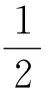
例2 (2017年福建省普通高中毕业班4月质量检查理数第10题)空间四边形ABCD的四个顶点都在同一个球面上，E,F分别是AB，CD的中点，且EF⊥AB，EF⊥CD.若AB=8，CD=EF=4，则该球的半径等于( ).

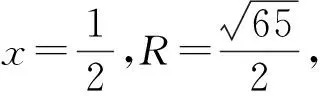
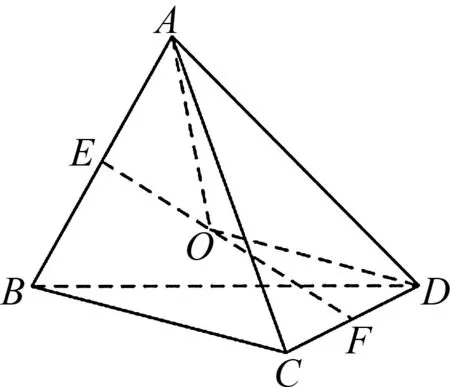
图1

评析：依循定义，先找出与部分顶点距离相等的点，进而判定这是与所有顶点距离相等的点，这是“依循定义等距定心”的关键.

2.补全形体，等距定心

将多面体的形体补全，如根据三条侧棱两两垂直，将四面体补成长方体或正方体；三对对棱两两相等，将四面体补成长方体等，则可根据对角线交点到各顶点的距离相等确定出球心，进而将问题轻松予以解决.

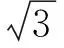
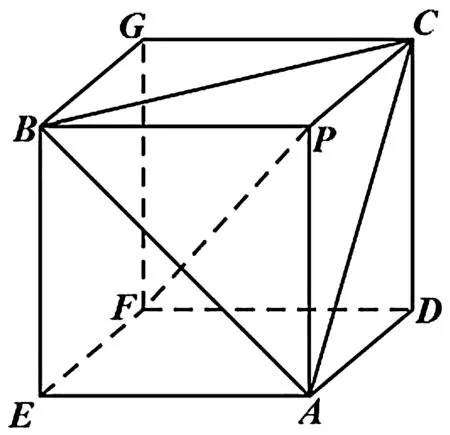
图2

例4 (2019年全国卷Ⅰ理科第12题)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，又E,F分别为PA,AB中点，∠CEF=90°，则球O的体积为( ).

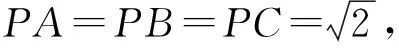
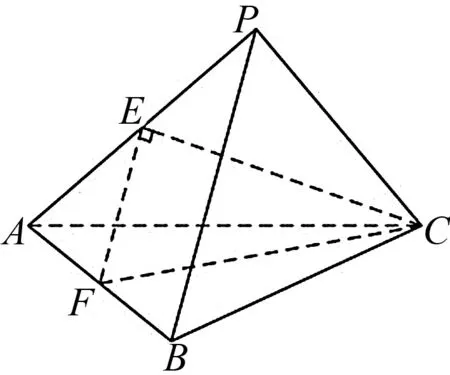
图3

评析：依据多面体的特征，判断这是哪一个形体的一部分，进而将其补全，这是“补全形体，等距定心”的关键.

3.找出投影，等距定心

根据球心到面上各个顶点的距离相等，可知球心在面上的投影到各个顶点的距离也相等，球心在过投影且垂直于平面的直线上，由此可过投影作对应平面的垂线，垂线的交点即为球心.

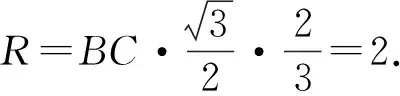
例6 (福州市2021年高中毕业班第一次质量检测第15题)在三棱锥P-ABC中，侧面PAC与底面ABC垂直，∠BAC=90°，∠PCA=30°，AB=3，PA=2.则三棱锥P-ABC的外接球的表面积为.

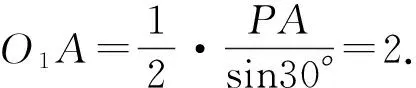
评析：解决此类问题关键在于两“心”(外心和球心)的确定，先确定面的外心，再确定球心，这是问题得以解决的关键.

4.以算代证，等距定心

当寻找或判定球心位置有难度时，我们可以以算代证，通过建立坐标系赋予顶点和球心坐标，进而通过等距得到方程，确定出球心位置.

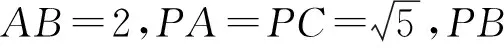
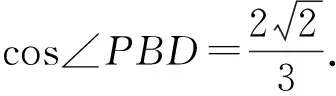
图4

评析：由于建系，我们赋予了点以坐标，将几何推证问题转化为代数运算问题，降低了空间想象的难度，使得解题具体形象，易于操作.

数学高考命题的原则是：以数学内容为主线，聚焦学生对重要概念,定理,方法,思想的理解和应用；注重数学本质,通性通法，淡化解题技巧.故我们在解题过程中，要引领学生如何利用数学本质来解题，而不是一味讲授解决此类问题应具备有什么样的技巧.只要基于问题本质，不管模型如何改变，题目如何变化，都会使学生从“山重水复疑无路”的窘迫中解脱，感受到“柳暗花明又一村”的惊喜.