一道2022年高考模考题的解法探究
2022-05-08江苏省启东市第一中学226200曹荣荣
江苏省启东市第一中学 (226200) 曹荣荣
二元条件最值问题可以很好的考查考生对高中数学不等式主干知识的掌握情况,及考生的数学运算能力和推理论证能力,因此在各类考试中备受命题者的青睐.
题目(2021年学年第一学期高三“山水联盟”开学联考试题第8题)已知实数x,y满足x2-2xy-3y2=1,则x2+y2的最小值为( ).
这是一道二元条件最值问题,主要考查利用基本不等式、重要不等式、三角换元法求最值,考查了考生的逻辑思维能力和运算求解能力,以下对这道试题进行多解探究,以期起到引导作用.
评注:将已知条件式子分解因式,再进行二元换元,分别表示出x和y,代入x2+y2,再运用重要不等式a2+b2≥2ab和不等式基本性质得出x2+y2的最小值.本解法比较基础,运用的是不等式中的主干知识,运算量比较少,体现了化归与转化思想中蕴含的复杂问题简单化的原则,有利于引导学生在不等式计算中把握运算规则.
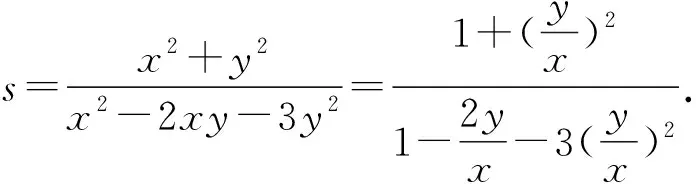
评注:本解法运用了判别式法,把待求式和已知式作商,再齐次化后换元,由判别式大于等于0,结合s>0,解不等式可得出s的最小值,从而得出x2+y2的最小值.本解法中蕴含了方程思想,有一定的思维层次,迁移了方程有实根与判别式符号的关系的知识,具有一定的运算量,有利于培养学生的运算求解能力和演绎推理能力.
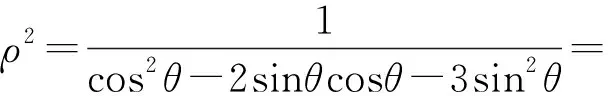

评注:本解法由待求式联想到三角函数平方关系式sin2α+cos2α=1,代入已知式子,进行三角换元,分离变量,最后运用辅助角公式得出分母的最大值,从而得出x2+y2的最小值.本解法通过三角换元,进行的三角恒等变换,培养学生的三角运算能力,提升数学运算的数学学科核心素养.

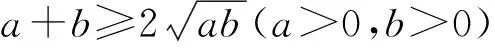
教师在平时的习题教学中,可以试着引导学生习题进行多解探究,通过比较多种解法优劣做到优化解题思路,使得解题活动变得有趣,提升学生的解题能力,培养学生的数学探究能力,促进学生提升数学学科核心素养.
