一道试题的探究与推广

重庆市铜梁二中 (402560) 李 波 禇晓渝

题目已知抛物线C:y2=2px(p>0)过点M(m,2)为其焦点为F，且|MF|=2.

(1)求抛物线C的方程；

(2)设E为y轴上异于原点的任意一点，过E作不经过原点的两条直线分别与抛物线C和圆F:(x-1)2+y2=1相切于点A,B，证明：A,B,F三点共线.

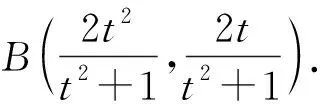
1 纵向探究

解析几何题目往往是某个一般规律的特例，这就要求我们不仅要会解题，更要求根溯源，揭示一般规律.上题中的圆F是以焦点F为圆心且与抛物线C相切的圆，经过探究，得到下面的结论.

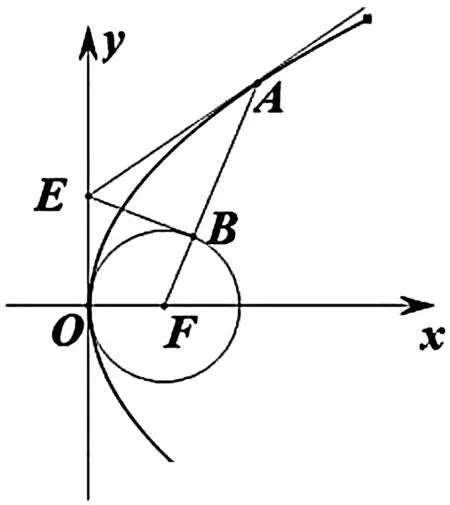
图1

2 横向类比

下面将性质1推广到椭圆上得到了更加优美的性质.

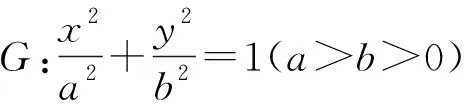
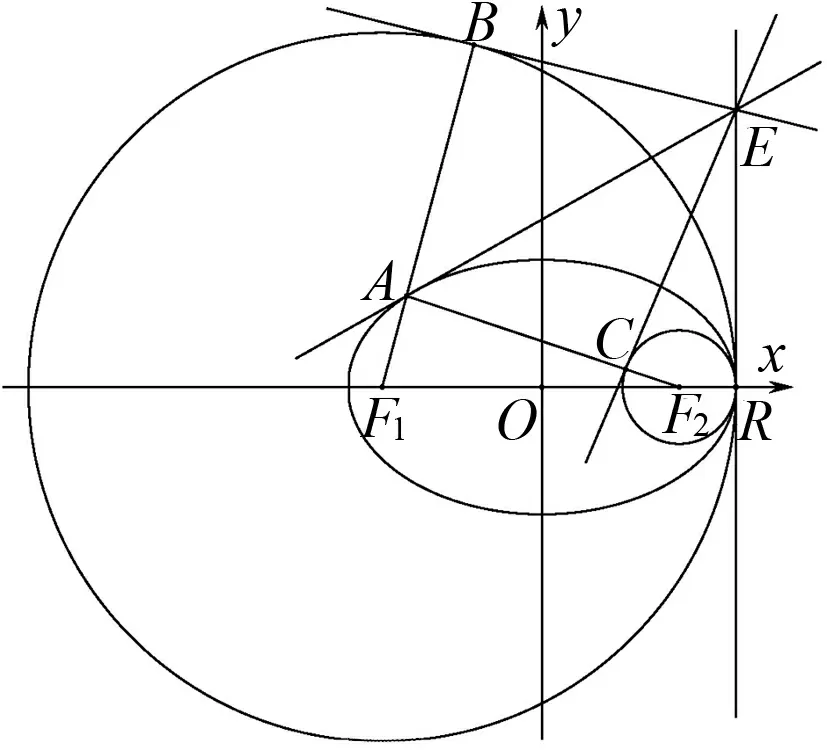
图2

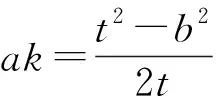
三 进一步的探究

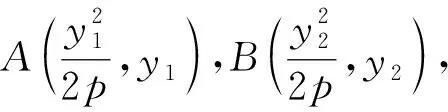
图4

(1)E1,E2的纵坐标之积为-(a-c)2且△E1FE2为直角三角形；

(2)E3,E4的纵坐标之积为-(a+c)2且△E3FE4为直角三角形；

(3)E1,F,E3共线，E2,F,E4共线；

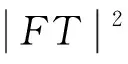
(2)类似于(1)的证明.

同理可证：E2,F,E4共线.

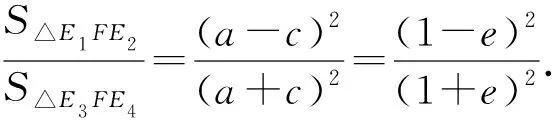
(1)E1,E2的纵坐标之积为-(a-c)2且△E1FE2为直角三角形；

(2)E3,E4的纵坐标之积为-(a+c)2且△E3FE4为直角三角形；

(3)E1,F,E3共线，E2,F,E4共线；

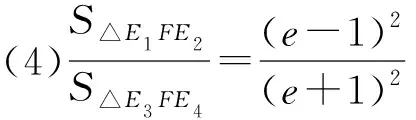
利用性质3和性质5，可以得到下面的结论.

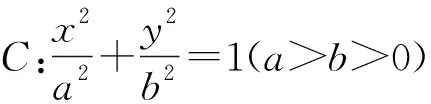
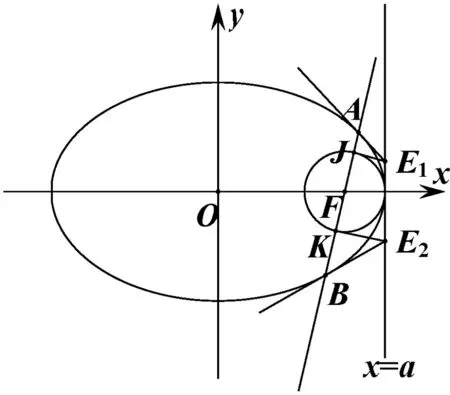
图5