椭圆中一类特殊三角形面积问题的推广

江苏省南京市燕子矶中学 (210038) 卢荣亮 岳 恒

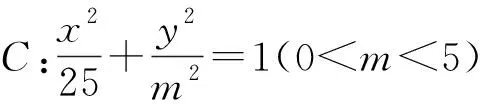
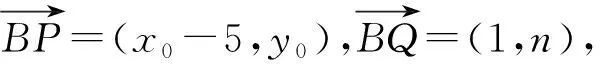
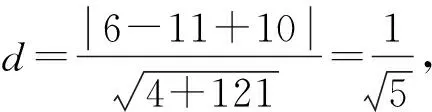
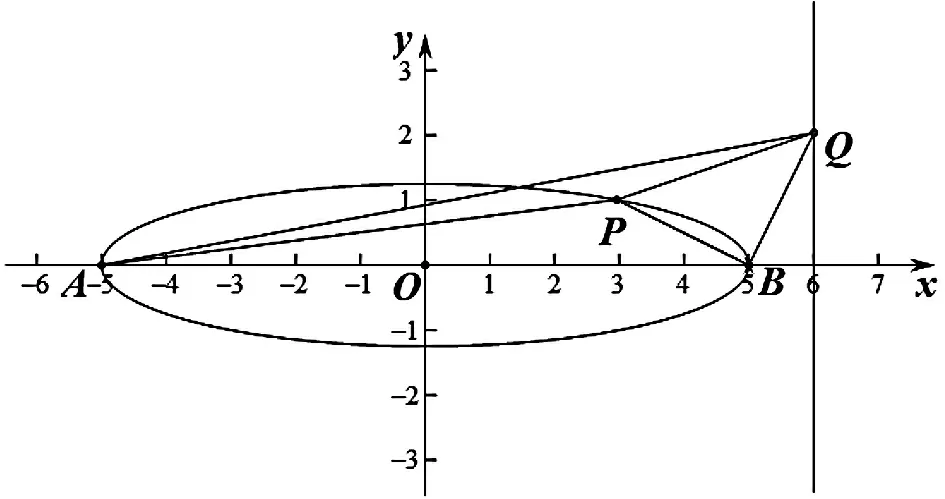
图1

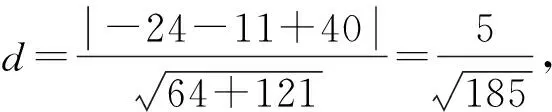
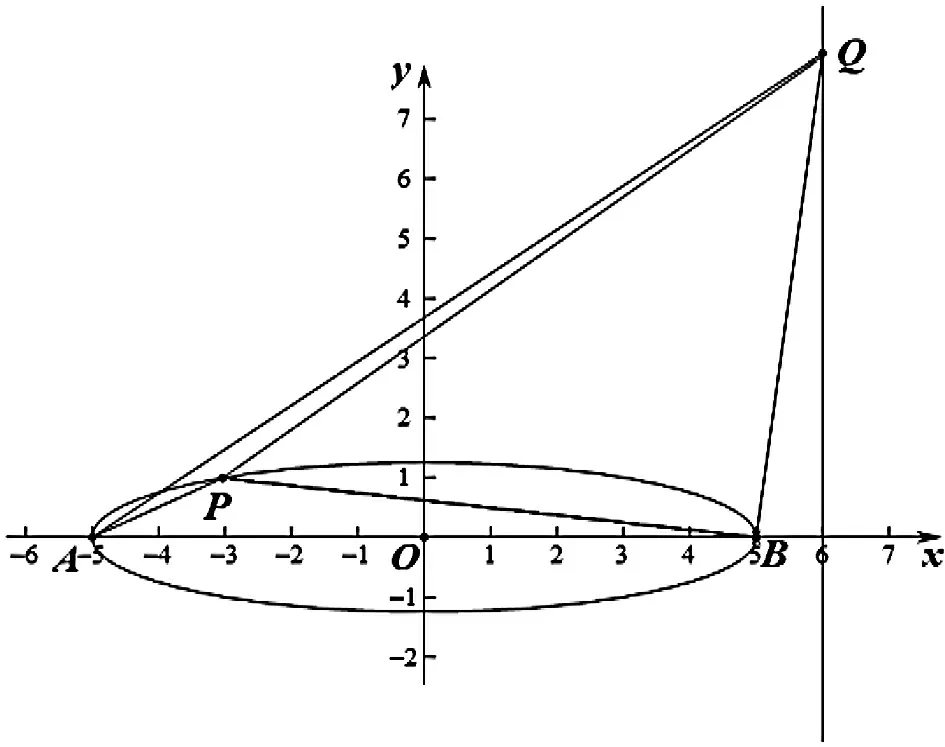
图2

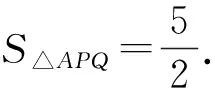
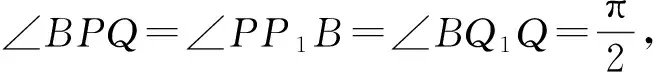
问1：点P横坐标在什么情况下唯一？点P横坐标在什么情况下有两解？点P在什么情况下又不存在呢？基于此，我们得到推论1.

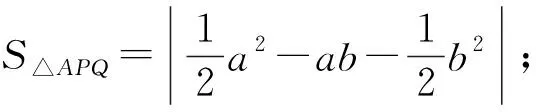
(3)若m>a+b，则点P不存在.

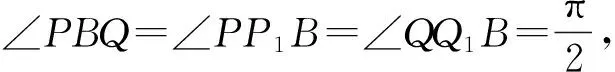
图3

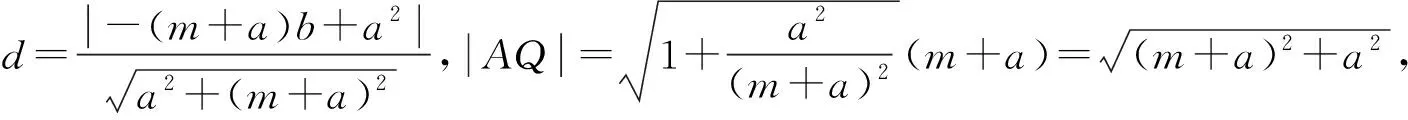
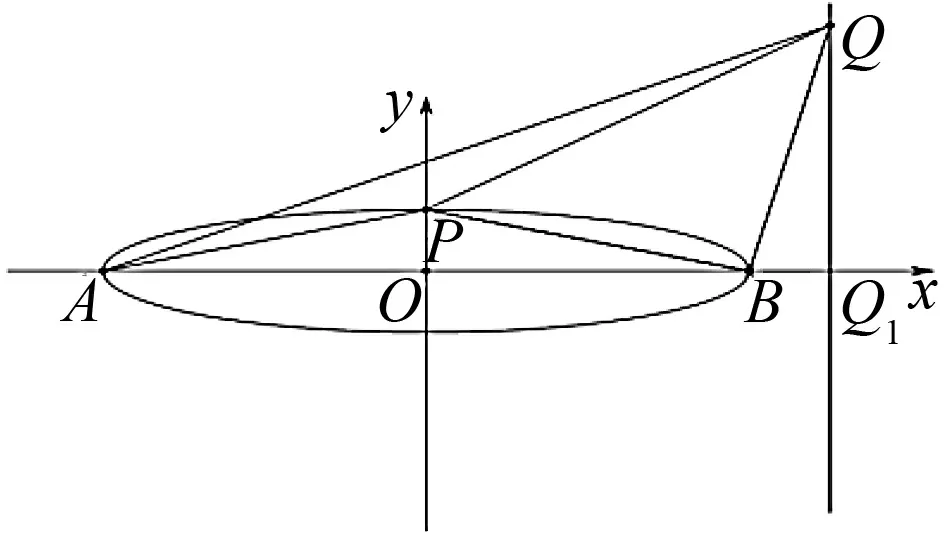
图4

(1)若a0.

①如图5，若点P(n,m-a)，则Q(m,a-n)，又因为A(-a,0)，则直线AQ方程为(a-n)x-(m+a)y+a(a-n)=0，所以点P到直线AQ距离

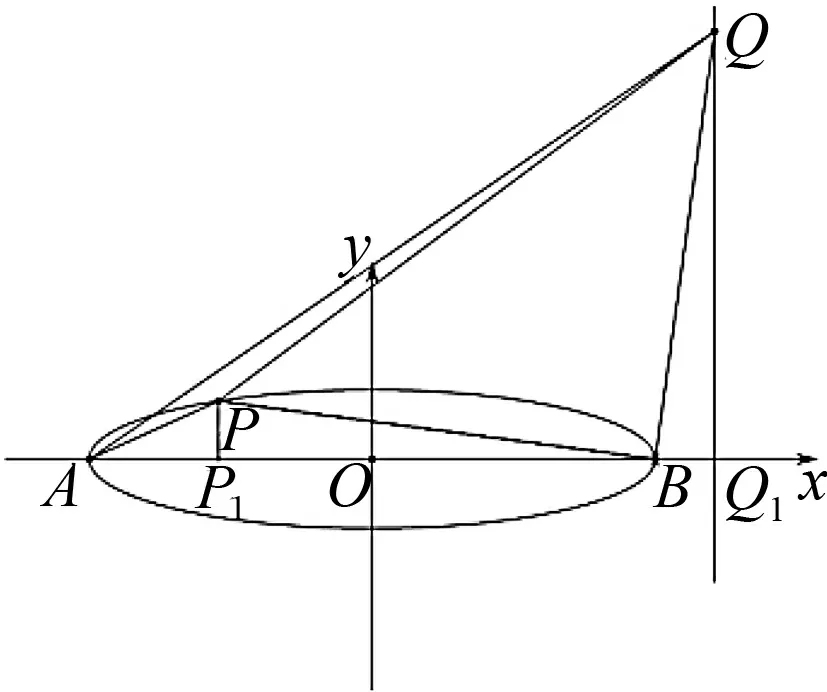
图5

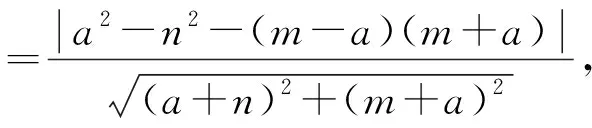
图6

(2)若m>a+b，则|PP1|=m-a>b，又因为0≤|PP1|≤b，所以点P不存在.

问2：若原条件“|BP|=|BQ|”改为“|BP|=λ|BQ|”，还有类似结论吗？基于此，我们得到推论2.

(3)若λ(m-a)>b，则点P不存在.

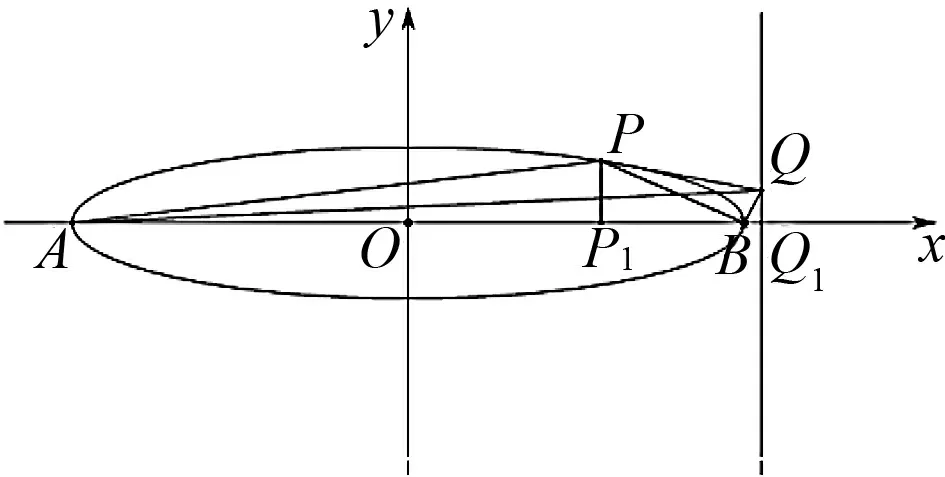
图7

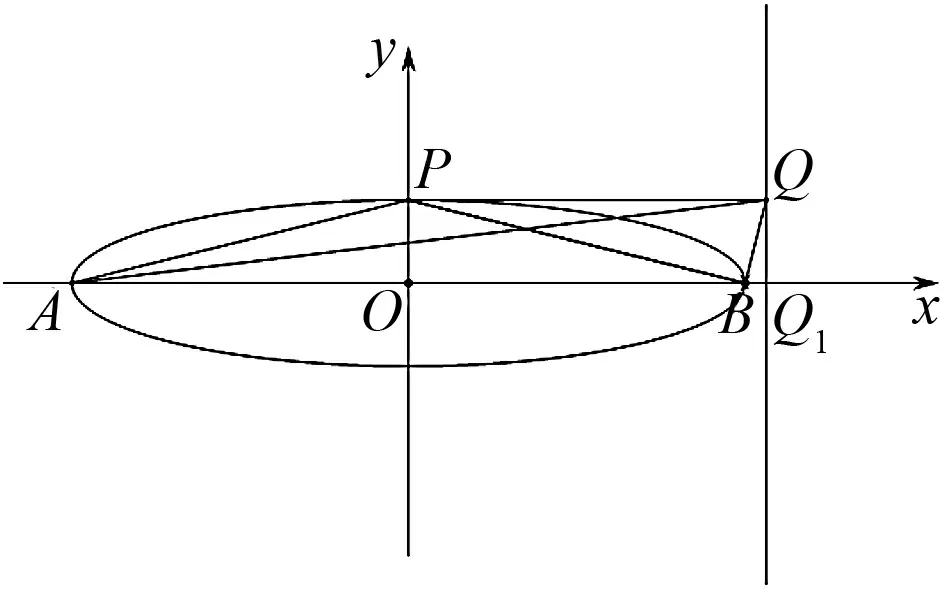
图8

(2)若0<λ(m-a)0.

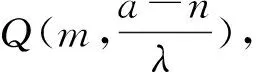
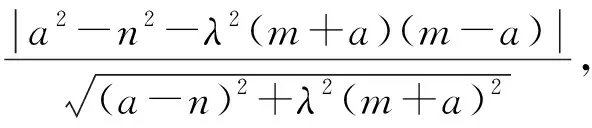
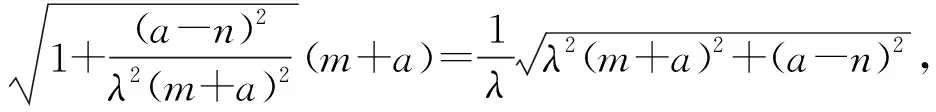
图9

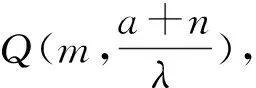
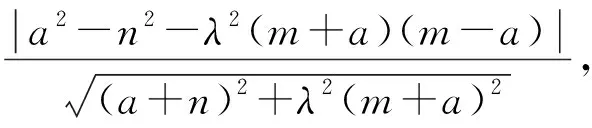
图10

(3)若λ(m-a)>b，则|PP1|=λ(m-a)>b，因为0≤|PP1|≤b，所以点P不存在.

注：当λ=1时，该结论就是推论1.

用“由特殊到一般”和“数学结合”的思想方法研究数学问题并不难，学生完全可以掌握，本文是由笔者和学生共同讨论而完成.在平时研究高考题的过程中，教师一个人研究，不如带领全班学生一起研究.在笔者所执教的班级中，每周带领学生研究一道高考题.在研究的过程中，笔者只需将自己平时研究数学问题的基本思想方法教给学生，变学生的“被动刷题”为“主动研究”，从而培养学生的数学核心素养，训练学生数学思维，提升学生的数学学习兴趣，同时又能促进自身的专业成长.