用逻辑纠正一道题的解答

江西省瑞金第一中学 (342500) 谢小平

题目：已知函数f(x)=log2x．

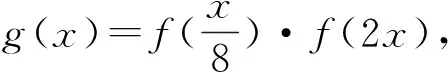
(2)若不等式f(k·2x)≥f(4x-k)在区间[1,2]有解，求实数k的取值范围．

这是一道高一期末考试题，命题者提供的解答如下：

(1)易得值域为[-4,+∞) (具体过程略)解.

争议的本质：题设应理解为区间[1,2]是定义域的子集，再确保不等式在区间[1,2]上有解？还是区间[1,2]与函数的定义域有交集，在确保不等式在交集内有解即可呢？对此先看如下问题：

已知区间D⊆E，则“不等式f[g(x)]>0在区间D有解”是“不等式f[g(x)]>0在区间E有解”的( ).

A.充要条件 B.充分不必要条件

C.必要不充分条件 D.既不充分也不必要条件

答案选B.若把题目的区间换成[0,2]，即若不等式f(k·2x)≥f(4x-k)在区间[0,2]有解，求实数k的取值范围.