基于数字控制器的石英挠性加速度计再平衡回路设计

袁文辉,王晓东,仇 斌,孙培华

（北京航天控制仪器研究所,北京 100039)

0 引言

石英挠性加速度计具有体积小、精度高的优点,目前使用最为广泛的模拟式伺服电路的输出一般为模拟电压或电流,需要与模数转换电路配合工作才能接入数字计算机系统,这种工作模式有两个缺点:1)转换电路存在转换误差且转换过程为开环工作模式,由此会引起转换精度损失;2)结构复杂、占用空间大。以上缺陷不利于未来惯性导航系统的高精度、微型化发展,研究脉冲输出型数字伺服电路能有效改善以上问题。

当前,石英挠性加速度计数字伺服电路核心组成部分主要为表头差动电容检测模块、数字信号处理模块和力矩器加矩模块。对表头差动电容的检测,主要的实现方法有谐振法[1]、载波电容调制解调法[2-4]、开关电容法[5]等;对摆片的控制策略主要有PI控制算法[6]、PID算法[7]、自适应PID算法[8]、最少拍无纹波算法[9]等。其中,最少拍无纹波控制算法仿真结果相比于PID算法具有更好的动态特性,但其控制本质依赖于被控对象的精确数学模型,在实际应用中难以达到预期的控制效果。

本文研制的数字伺服电路应用了单载波开关电容充放电调制、滑动平均滤波算法解调的电容检测方案,由现场可编程门阵列（Field Programmable Gate Array,FPGA)生成方波作为载波信号对差动电容进行充放电,极大地简化了电路结构,对调制后的电容信号进行周期性数字滑动平均处理,提高了电容检测的增益和稳定性;采用线性自抗扰控制（Linear Active Disturbance Rejection Control,LADRC)算法对石英摆片组进行控制,能够有效跟踪摆片的位置和速度信息以及系统总扰动,基于以上方案研制的数字伺服电路具备高精度、高动态特性。

1 数字伺服电路闭环检测系统组成及原理

1.1 系统组成

石英挠性加速度计数字伺服电路的结构如图1所示。当加速度作用于加速度计表头时,摆片在惯性力作用下偏离平衡位置而与电容传感器形成差动电容,由电容检测电路将差动电容值转化为电压差值,A/D转换器将电压差值转化为数字量作为数字控制器（FPGA)的输入,实现差动电容检测,控制器计算结果一方面以脉冲的形式输出表征加速度的大小,一方面输入至D/A转换器转化为电压值,通过V/I转换电路转化为直流对力矩器进行加矩,实现对摆片的控制。

图1 数字伺服电路原理框图Fig.1 Principle block diagram of digital servo circuit

1.2 差动电容检测原理

目前,石英挠性加速度计数字伺服电路电容检测应用最为成熟的方案为单载波调制解调法,其原理如图2所示。由载波生成电路产生载波信号,将微弱的电容信号调制到高频的载波信号中,通过后续的解调电路还原电容信号,但该方法电路结构相对复杂且对器件对称性要求较高。

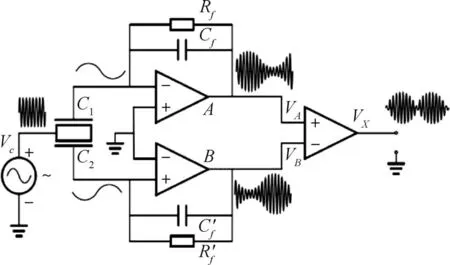
图2 单载波电容调制电路原理图Fig.2 Schematic diagram of single carrier capacitance modulation circuit

本文提出了一种单载波调制、电容充放电式的差动电容检测方案,其原理如图3所示。由FPGA生成幅值为0V～3.3V、频率为6kHz的方波作为载波信号,该信号通过两个相同电阻同时对石英挠性加速度计表头中的差动电容极板进行充放电,两路电容的电压值分别接入差分仪表放大器进行差分运算,运算结果通过A/D转换为数字量输入至数字控制器FPGA中进行数字解调,从而实现差动电容检测。该方案具有两个优点:1)结构简单,有利于电路的小型化;2)对器件的对称性要求相对较低,载波频率较低,因而对后续差分运放的压摆率要求不高,实际中只需保证两个充电电阻具有较好的对称性即可。

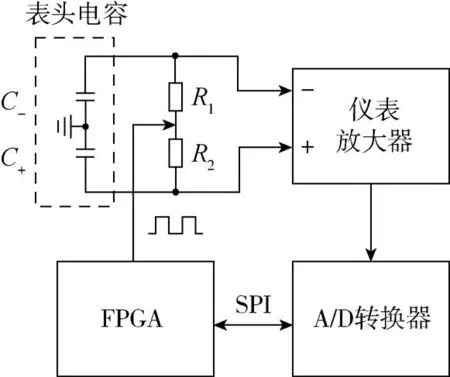
图3 差动电容检测原理图Fig.3 Schematic diagram of differential capacitance detection

1.3 力矩器加矩

力矩器加矩的原理如图4所示。线性自抗扰控制器的输出由D/A转换器转化为模拟电压值,经过运算放大器作用,电流一方面通过精密电阻Rs形成回路,一方面输入至力矩器线圈。固定于摆片两侧的线圈中通有直流时能与力矩器中的磁钢形成电磁力,该电磁力用于平衡由外界加速度作用产生的惯性力,推动摆片回到平衡位置。

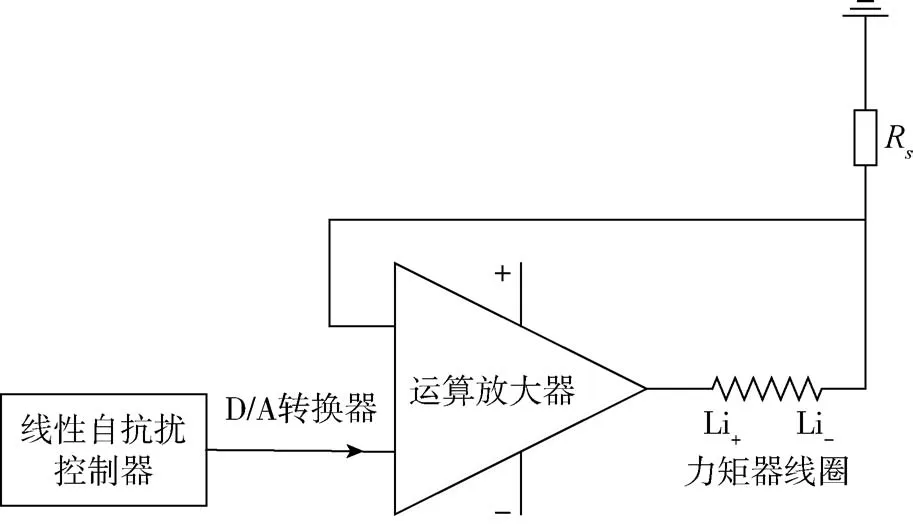
图4 力矩器加矩原理图Fig.4 Schematic diagram of torque added to torquer

1.4 数字控制器

传统的模拟式伺服电路难以实现相对复杂的控制算法且电路结构复杂、抗干扰能力弱,采用数字式的方案能有效克服模拟电路的不足。本文以FPGA作为数字控制器,基于Verilog语言实现载波生成、与A/D和D/A芯片的数据交换、差动电容解调、滑动平均滤波算法、LADRC算法和脉冲输出功能,信号处理过程如图5所示。

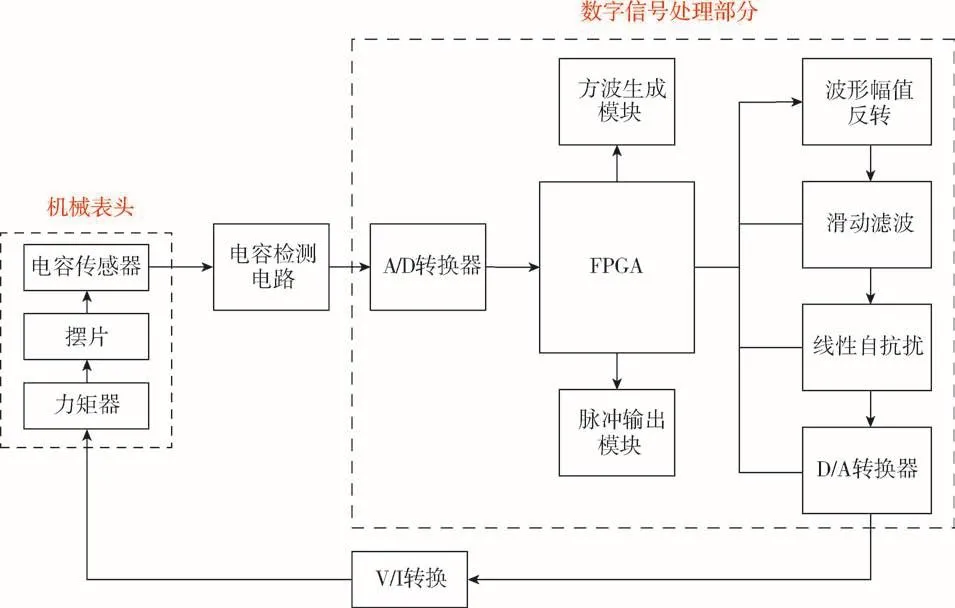
图5 数字信号处理流程图Fig.5 Flowchart of digital signal processing

在石英挠性加速度计数字伺服电路中,表头差动电容的检测和摆片的控制精度是影响最终加速度测量结果的两个关键因素,下面重点介绍实现过程。

2 差动电容调制解调

电容传感器检测到的差动电容值可以表征加速度计敏感到的外界加速度大小,电容检测精度直接影响加速度测量结果。在石英挠性加速度计中,摆片在平衡位置时电容值一般为几十皮法（pF),受加速度作用电容变化量能达到飞法（fF,1fF=1×10-3pF)甚至阿法（aF,1aF=1×10-6pF)级别,如此微弱的电容信号极容易淹没在干扰电容中。本文将微弱的电容信号调制到高频载波中,然后通过数字解调过程还原过程电容信号,达到微弱电容检测的目的。

2.1 电容信号调制过程

对于平板电容,当通过电阻R、0V～3.3V方波信号对其进行充放电时,电容充电过程电容电压随时间的变化关系如式（1)所示,电容放电过程电容电压随时间的变化关系如式（2)所示。

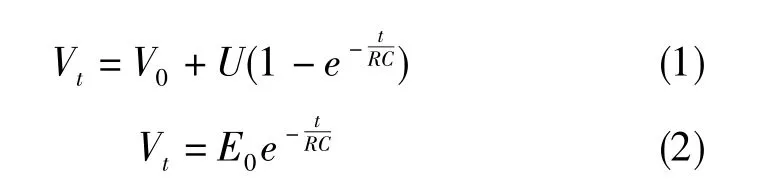
式（1)、式（2)中,U为电容充电时的终值电压,E0为电容放电时的初始电压。

在方波信号作用下,电容充放电波形如图6所示。

当有加速度输入时,石英摆片在惯性力作用下偏离平衡位置,摆片距离两侧极板间距不同,两路电容充放电速度不一致,且电容差值越大,充放电速度差异越大,其过程如图7所示。

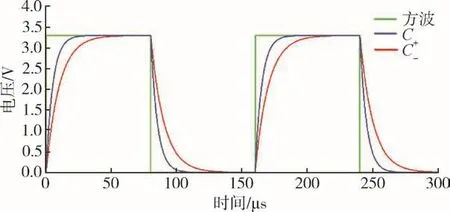
图7 加速度作用下差动电容充放电示意图Fig.7 Diagram of differential capacitance charge and discharge under acceleration

2.2 电容信号数字解调过程

两路电容分别接入差分运算放大器输入端进行差值计算,计算后的波形如图8所示,计算结果作为A/D转换芯片的输入。一个方波周期内A/D芯片进行N次采样,将模拟量转换为数字量输入到FPGA进行计算,经过FPGA反相、滑动平均滤波处理后表征出电容差值大小。

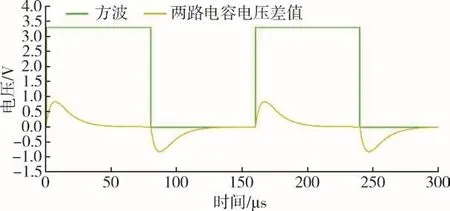
图8 差分运放输出Fig.8 Output of differential amplifier

（1)反相

根据电容充放电特性,一个方波周期内的电容电压差值总是一半为正,另一半为负。考虑后续的滑动平均滤波算法,需要对每个方波周期内一半的波形进行反相,此过程通过FPGA数字化运算实现,反相后的波形如图9所示。经过运算后,表征电容电压差值的数字量在每个方波周期内均为正值或负值,其符号能反映出表头差动电容的大小关系。

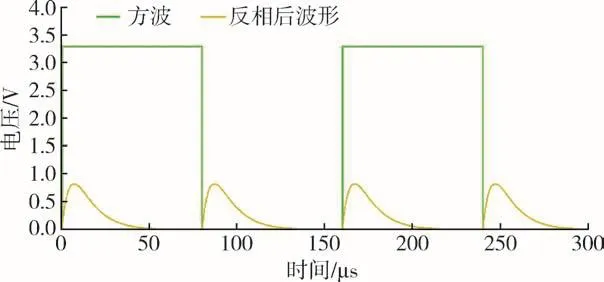
图9 波形反相结果Fig.9 Result of reversed waveforms

（2)滑动平均滤波

由前面的分析可知,波形反转后一个方波周期内电压曲线与时间轴围成的面积大小可以表征电容差值的大小。为求其面积,可以对反转后一个方波周期内A/D采集到的离散点进行累加,即算术平均的思想。但该方法每N个采样点才能输出一个结果,严重影响系统的响应速度。本文采用滑动平均滤波算法,其原理如图10所示。内存中存储N个采样数据点为一个队列,此后每采集一个新数据,就将队列中最早采集的一个数据点移除,而后计算包括新数据在内的N个数据的算数平均值。

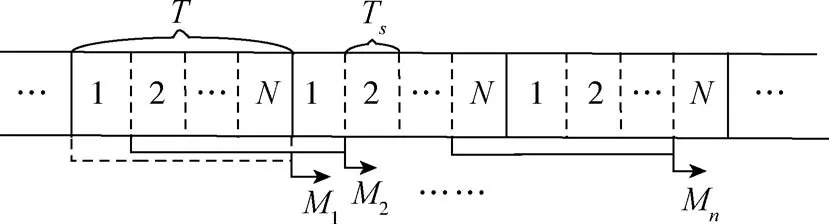
图10 滑动平均滤波原理图Fig.10 Schematic diagram of moving average filter

图10中,T为波形反转后的输出信号周期,Ts为A/D采样周期,Mi为每一次滑动平均后的计算结果。相比于算数平均,该方法每采集一个数据点就能输出一个结果,滤波阶数越高则输入采样值越准确,经过运算后的输出值也更精确,数字伺服系统的稳定性越好。然而过高阶的滤波会影响系统的动态特性,故滤波阶次应在保证稳定性的前提下尽可能的高。经过数字滑动平均滤波处理后的实测结果如图11所示,其值越大,表征加速度计表头差动电容差值越大,至此完成差动电容的检测过程。

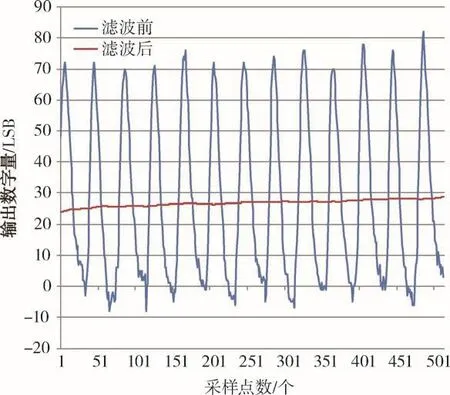
图11 滑动平均滤波前后对比图Fig.11 Results of moving average filter

3 基于线性自抗扰控制的摆片控制方法

目前对石英挠性加速度计摆片的控制算法主要为PID控制,该方法是将偏差e的比例、积分和微分进行线性组合形成控制量u,对被控对象进行控制的一种控制方法。该方法具有不依赖被控对象准确的数学模型、参数物理意义明确等优点,但响应快速性和超调之间存在一定矛盾,特别是在石英挠性加速度计摆片控制过程中,摆片的活动间隙一般为17μm～21μm,过大的超调容易导致控制过程中摆片与两侧力矩器发生碰撞,出现打摆现象。考虑经典PID控制的缺陷,本文提出采用线性自抗扰控制算法对石英摆片进行控制。

3.1 线性自抗扰控制

线性自抗扰控制[10]（LADRC)是一种基于状态反馈的线性控制策略,其结构如图12所示。控制器的核心为状态观测器（Linear Extended State Observer,LESO),控制信号u和系统输出y为LESO的两个输入,z1、z2、z3为LESO的输出,分别为y、y·和系统总扰动的观测值。

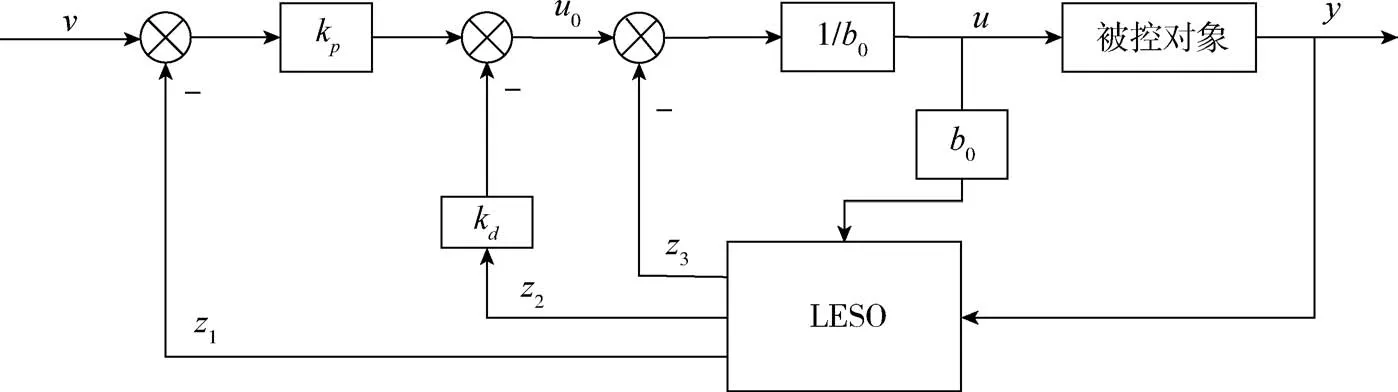
图12 线性自抗扰控制结构图Fig.12 Structure diagram of linear active disturbance rejection control

离散形式的LESO为

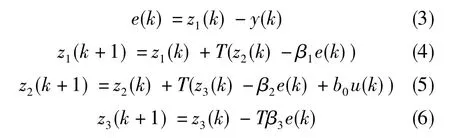
线性控制律为

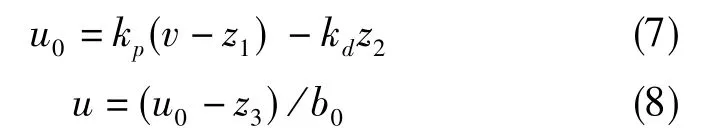
式（3)～式（8)中,T为采样周期,v为期望的输出。在加速度计摆片控制系统中,LADRC控制器的输入y表征石英摆片的位置,期望位置v为两电容极板的中心。 kp、 kd、 b0、 β1、 β2、 β3为需要整定的控制系统参数,实际工程应用中,可以采用带宽法[11]进行参数的调节,通过极点配置的方法,让控制器增益kp、kd的选取与控制器带宽（ωc)相关, 让观测器增益β1、 β2、 β3的选取与观测器带宽ω0相关,满足关系式kp=、 kd=2ωc、β1=3ω0、 β2=3、 β3=, 通过调节 b0、 ωc、 ω0完成闭环控制系统参数的调节过程。

石英挠性加速度计线性LADRC控制系统框图如图13所示。滑动平均滤波的输出结果作为控制器的输入y,当摆片未处于平衡位置时,摆片与两侧电容极板间距不一致使得差动极板电容值大小不同,因此滑动平均滤波后的计算结果不为零。经LADRC计算后,后续模块输出相应大小的电流值,该电流值流经力矩器线圈产生电磁力推动摆片回到平衡位置。

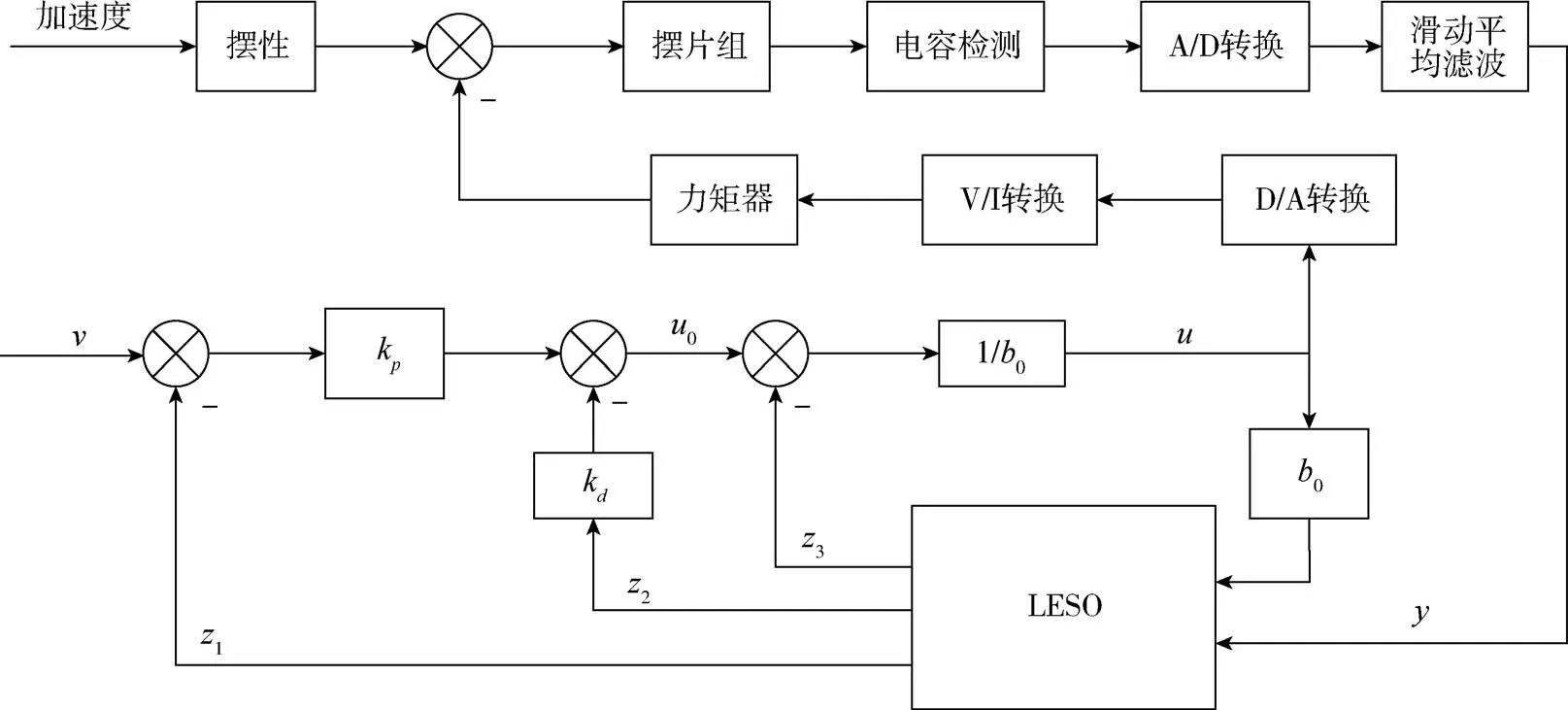
图13 LADRC结构框图Fig.13 Structure block diagram of LADRC

3.2 仿真分析

对闭环系统进行仿真,以滑动平均滤波后的输出y作为LADRC的一个输入,对摆片施加阶跃信号,与PID控制算法的对比仿真结果如图14～图16所示。

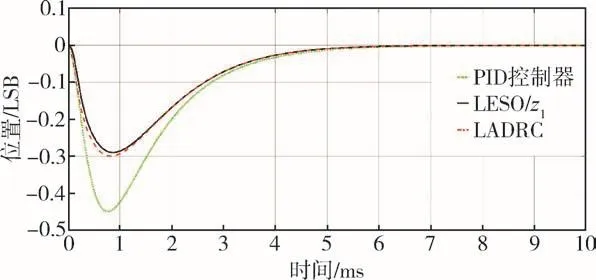
图14 摆片位置Fig.14 Diagram of pendulum position

图15 摆片速度Fig.15 Diagram of pendulum velocity

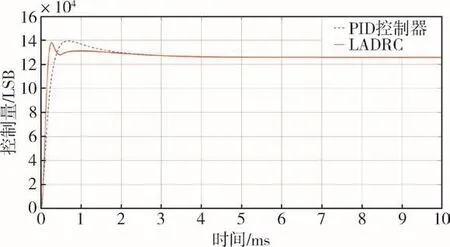
图16 控制信号波形图Fig.16 Waveform of control signal

由仿真结果可知,在外部输入为阶跃信号时,z1能够精确地跟踪摆片的位置信号,在t=5.5ms时,摆片达到平衡位置,稳态时无静差;z2跟踪摆片的速度,t=6ms时,摆片速度趋近于零;控制量u的波形表现为典型的阶跃响应曲线,调节时间约2.5ms,超调量9.8%。与经典PID控制算法相比,LADRC响应速度更快,相同加速度作用下摆片偏离平衡位置最大值减小33.2%。以上结果表明,LADRC可以用于石英挠性加速度计的摆片控制中,且响应速度快,控制效果更稳定。

4 试验验证

首先,对传统模数转换电路中普遍采用的I/F转换方案进行了性能测试,分析转换过程的精度损失。然后,根据 《GJB 1037A-2004单轴摆式伺服线加速度计试验方法》[12]规定的加速度计试验方法对研制的样机进行了电路特性测试和性能测试。最后,将本文研制的数字伺服电路与传统模拟式伺服电路的精度进行了对比分析。

4.1 模数转换电路测试

以精密恒流源作为输入,测试某型号电流/频率（I/F)转换电路的转换精度,测试结果如表1所示。转换电路的非线性误差、温度系数等指标均为10-6量级,而石英挠性加速度计的部分指标能达到甚至优于10-6量级,将加速度计的输出通过I/F转换电路转化为数字量的方案会由于转换电路的精度等级不同而产生不同的精度损失。

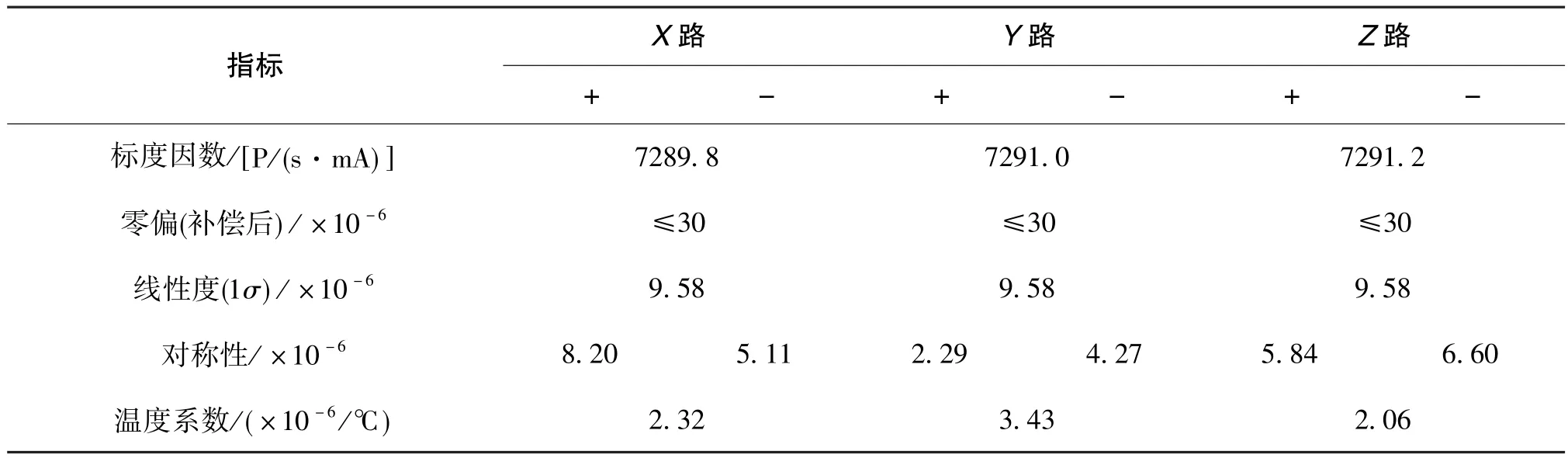
表1 I/F电路实测结果Table 1 Test results of I/F circuit

4.2 电路跟踪特性测试

利用电激励模拟外界输入加速度,电激励的接线图如图17所示。信号发生器通过限流电阻Rr对力矩器线圈施加电流值模拟外界加速度的变化情况,利用示波器观测采样电阻Rs两端的电压信号,分别测试数字电路对阶跃信号和正弦波信号的跟踪特性,实测实物图如图18所示,实测结果如图19～图21所示。

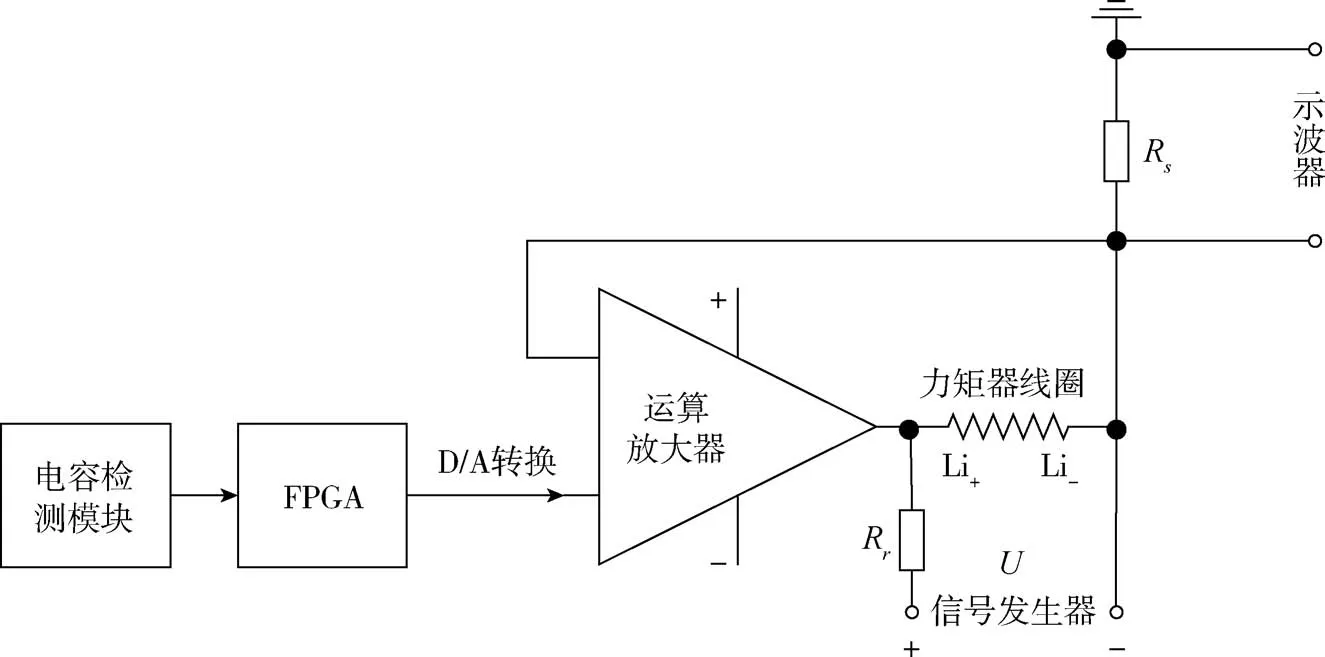
图17 电激励接线图Fig.17 Connection diagram of electric excitation

图18 阶跃响应实测实物图Fig.18 Physical diagram of step response experiment

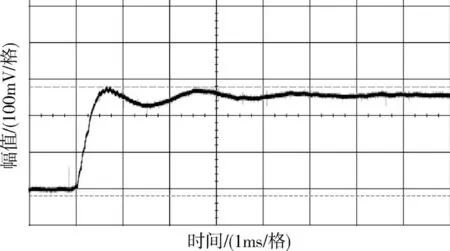
图19 实测闭环阶跃响应曲线Fig.19 Experiment result of closed-loop step response curve

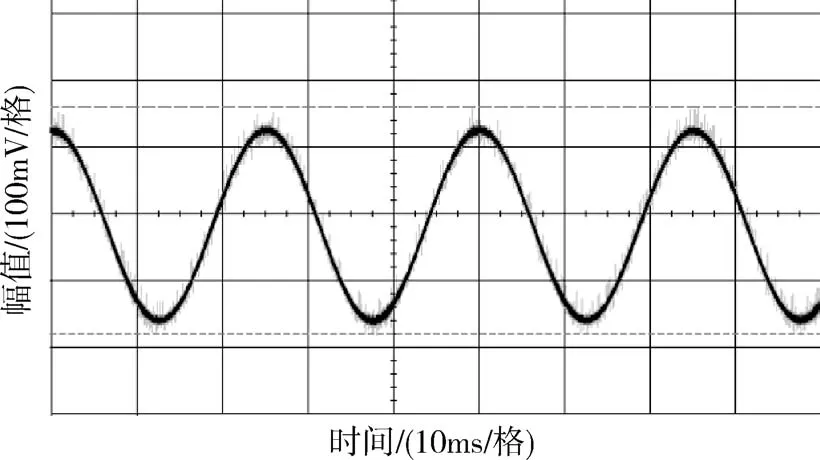
图20 40Hz正弦波跟踪效果图Fig.20 Tracing result of 40Hz sinusoidal wave

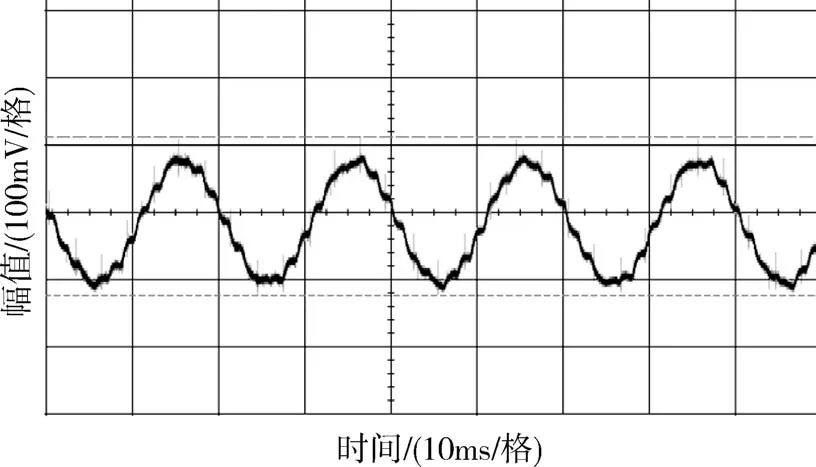
图21 截止频率正弦波跟踪效果图Fig.21 Tracing result of sinusoidal wave with cut-off frequency

该部分的测试结果表明:闭环系统阶跃响应上升时间为0.6ms,调节时间约3ms,超调量11%,系统带宽为976Hz。

4.3 分辨率测试

将研制的数字伺服电路与石英加速度计表头相连,在光栅分度头上测试整机的分辨率,在零位附近以3μg步进转动分度头,测试的实物图如图22所示,加速度计分辨结果如图23所示。

图22 分辨率测试实物图Fig.22 Physical diagram of resolution experiment

加速度每变化3μg,脉冲输出理论值变化12个,当实测值达到理论值的50%～150%时,可以认为加速度计能分辨出该加速度值。实测结果表明:逆时针转动分度头实测脉冲变化值分别达到了理论值的58%、92%、67%,顺时针转动分度头实测脉冲变化值分别达到了理论值的125%、117%、108%。由以上结果可知,本文研制的石英加速度计数字电路能够有效辨别出3μg的加速度变化值,即分辨率为3μg。

4.4 稳定性测试

分别在0g/1g加速度作用下每60s记录一次脉冲输出值,加速度计脉冲输出当量为12378个/（g.s),测试结果如图24、图25所示。

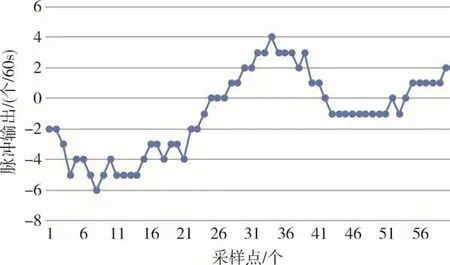
图24 0g稳定性测试结果Fig.24 Experiment result of stability under 0g condition

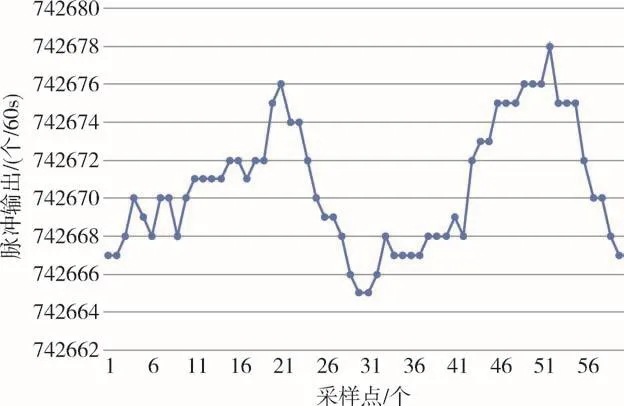
图25 1g稳定性测试结果Fig.25 Experiment result of stability under 1g condition

0g/1g加速度作用下标准差分别为3.013μg、3.279μg,则1σ准则下本文的数字伺服电路0g/1g稳定性分别为4.06μg、 4.41μg。

4.5 对比分析

采用相同的方法对同款加速度计配合模拟伺服电路进行连接并测试相同指标,测试结果汇总如表2所示。由测试结果可知,本文研制的数字伺服电路各项指标基本达到了模拟伺服电路水平。

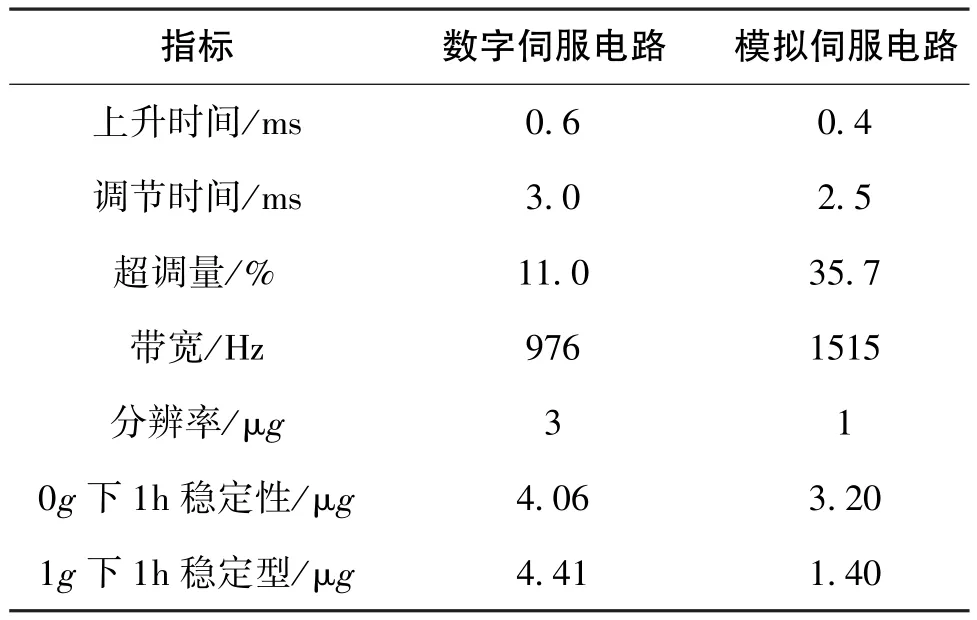
表2 两种电路对比结果Table 2 Comparison results of two circuits

5 结论

本文研制了一种基于电容充放电的石英挠性加速度计数字伺服电路,以FPGA作为数字控制器完成了加速度的数字化检测方案。文中提出的滑动平均滤波算法和线性自抗扰控制算法能够有效实现微弱电容检测、石英摆片控制的功能,制作的样机分辨率可达3μg,0g/1g稳定性分别为4.06μg和4.41μg,系统带宽为976Hz,兼具良好的动态特性和精度。