光子纠缠光纤陀螺的光路互易性分析

张桂才,冯 菁,马 林

（天津航海仪器研究所,天津 300131)

0 引言

在干涉测量中,给定有限的资源（如光功率或光子数等),相位检测灵敏度受光源或探测过程的统计不确定性限制。研究证明,传统光纤陀螺采用光的经典态（比如激光器和宽带光源),相位灵敏度受散粒噪声限制[1]:Δϕ=1/。其中,Δϕ为相位误差,N为Sagnac干涉仪的输入光功率（或输入光子数)。另一方面,量子干涉测量技术采用光的非经典态[2-4],基于被探测光子的纠缠特性,导致一种缩短的de Broglie波长,理论上可以突破经典光纤陀螺的散粒噪声极限,达到Heisenberg极限:Δϕ=1/N,这为光纤陀螺提供了一种新的精度提升途径[5-7]。

众所周知,传统光纤陀螺采用一个宽带光源和一个探测器,输入/输出共用Sagnac干涉仪的一个端口,这种结构构成一种互易性光路,使Sagnac干涉仪中的两束反向传播的光束具有相同的传输特性[1,8],也即各种因素引起的两束光的附加相移相同。采用互易性结构使传统Sagnac干涉仪的相位测量精度远超其它类型的光纤干涉仪,能够检测出优于10-7rad～10-8rad（量级)的微小相位差。另一方面,光子纠缠光纤陀螺同样存在互易性问题。一般情况下,光子纠缠光纤陀螺需要采用双端口输入/双端口输出的光路结构,这种光路结构与传统光纤陀螺完全不同,是否具备互易性尚未被人们充分认识。

光子纠缠光纤陀螺作为一项前沿技术,目前尚处于原理论证和理论探索阶段,相关文献报道还很少,且主要集中在Heisenberg极限灵敏度的理论分析方面,个别实验报道虽已产生量子增强效果,但其精度和实验手段距离实用还较远。本文主要对光子纠缠光纤陀螺的原理和误差机制进行研究,针对光子纠缠光纤陀螺通常采用双端口输入/输出的光路特征,利用散射矩阵模型分析了非理想分束器的相位特性,理论推导了各种非经典输入态的二阶符合输出光强。在此基础上,首次研究了光子纠缠光纤陀螺的光路互易性。

1 光子纠缠光纤陀螺的光路结构

1.1 传统光纤陀螺的光路互易性

传统光纤陀螺的光路结构如图1所示,分束器（2×2光纤耦合器)和光纤线圈共同构成Sagnac干涉仪（其它部分未示出)。Sagnac干涉仪有两个输入/输出端口,分别称为端口1和端口2。端口1的输入场为a1,端口2没有输入场,则从端口1输出的顺时针（cw)光波前后两次通过光纤耦合器,先经历一次透射（传输)过程再经历一次耦合过程;从端口1输出的逆时针（ccw)光波先经历一次耦合过程再经历一次透射（传输)过程。两束反向传播光波各经历了一次耦合和一次传输,累积相位差为零,经典干涉输出（端口1)必为中心明纹（1+eiϕ)形式。从端口2输出的顺时针（cw)光波两次通过光纤耦合器,两次经历透射（传输)过程;而从端口2输出的逆时针（ccw)光波则两次经历耦合过程。由于耦合光束相对反射光束存在相位差（理想情况下为π/2),这意味着即使陀螺静止,两束反向传播光波之间也存在一个π弧度的累积相位差,干涉输出必为中心暗纹 （1+ei（π+ϕ)=1-eiϕ) 形式。 传统光纤陀螺能够检测10-8rad（量级)的微小相位,这意味着这个π弧度的相位差也应具有相同量级的稳定性。但实际中,光纤耦合器存在插入损耗,且插入损耗和分光比通常是不稳定的,受环境温度、振动等的影响很大,这个π弧度的相位差也是不稳定的,会在陀螺中产生较大的误差或漂移。因此,在传统光纤陀螺中,端口1通常称为互易性端口,既是输入信号端口,也是输出信号端口,而端口2称为非互易端口。传统光纤陀螺这种输入/输出共享一个端口的互易性光路结构确保了两束反向传播光波经过光纤耦合器时历经的耦合相移和传输相移相等,从而使干涉信号的固有累加相移抵消为零,这是传统光纤陀螺与其它光纤干涉仪（如M-Z干涉仪)相比具有较高相位检测灵敏度的主要原因。

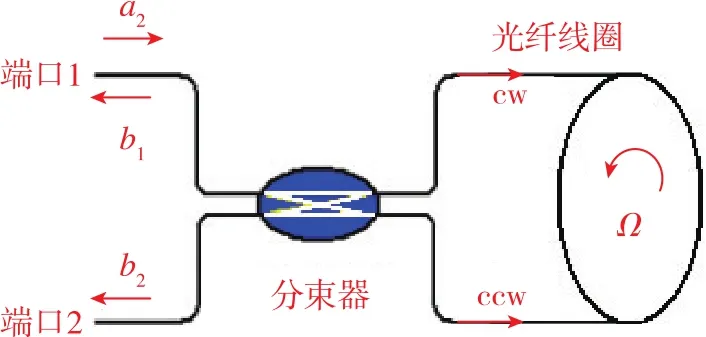
图1 传统光纤陀螺的互易性结构Fig.1 Reciprocity structure of classical fiber optic gyroscope

1.2 采用双环行器的光子纠缠光纤陀螺

在光子纠缠Sagnac干涉仪中,需要两个输入端口和两个输出端口,以便实现二阶符合计数。实际中,为了实现输入和输出模式的有效分离,提出了一种采用双环行器的Sagnac干涉仪结构,如图2所示。

图2 采用双环行器的光子纠缠Sagnac干涉仪Fig.2 Photon entangled Sagnac interferometer with double circulators

在量子理论中,输入/输出场振幅均用湮灭算符表示,因为这些算符的行为类似经典场中的复数场表示。假定a1、a2为对应端口1和端口2的输入,b1、b2为相应端口的输出。a1、a2、b1、b2对经典来说是场振幅,对量子来说是场的湮灭算符,则Sagnac干涉仪的输入输出关系为

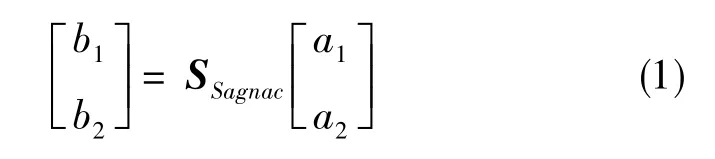
式（1)中的传输矩阵SSagnac可以写为[9]

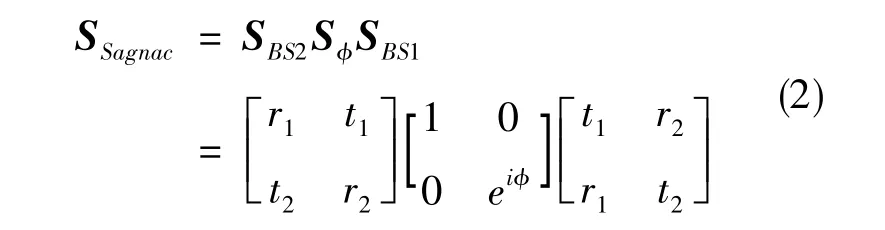
式（2)中,SBS1为光第一次经过分束器时的传输矩阵,SBS2为光第二次经过分束器时的传输矩阵,ϕ为旋转引起的Sagnac相移,Sϕ为光纤线圈（可以看成一个相移器)的传输矩阵,（t1,r1)和（t2,r2)分别为从分束器两侧输入时的振幅透射系数和振幅耦合系数。对于分立光学元件或空间光学元件,分束器可由半透半反镜构成;对于光纤器件,分束器是一个2×2光纤耦合器。其中,半透半反镜的透射光束对应光纤耦合器的传输光束,半透反射镜的反射光束对应光纤耦合器的耦合光束,两者的分析模型相同。

在分析量子分束器时,同样用场的湮灭算符a1、a2、b1、b2分别表示输入和输出,分别为与之对应的创生算符,则输入/输出关系写成矩阵形式为

由于分束器的互易性, 有φ1= φ2、ψ1= ψ2。通常认为反射镜厚度为零,则反射相位相对透射相位的相位差:ψ1- φ1= ψ1、ψ2- φ2= ψ2。因此,对于无损耗分束器,由式（7)得到: ψ1= ψ2= π/2。

2 非理想分束器相位特性的散射矩阵分析

2.1 分束器的散射矩阵模型

实际分束器通常是不理想的,这表现为光纤耦合器存在插入损耗和分光比不等于50:50。其传输矩阵不再是幺正矩阵,耦合光束相对传输光束的相位关系也将偏离π/2。可以用散射矩阵分析非理想分束器的传输特性[10-11],如图3所示,对于含有4个端口的光纤耦合器,不考虑内部反射,则其散射矩阵S为

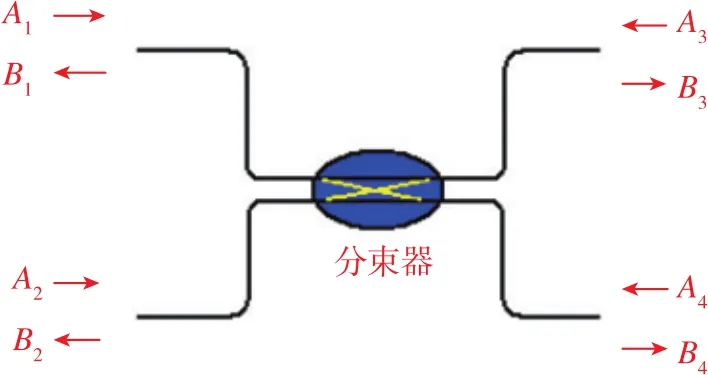
图3 光纤耦合器的散射矩阵模型Fig.3 Scattering matrix model of optical fiber coupler

式（8)中,Sij为耦合器散射矩阵的元素。

式（11)中,D=[I]-[S]H[S]为耗散矩阵。对于含有损耗的光纤耦合器,[A]H[A]-[B]H[B]>0,因此式（11)为正定二次型。由于DH=D,所以D为厄密矩阵。根据矩阵理论,实域上实对称矩阵及其正定二次型性质可以推广到复数域的厄密矩阵及其正定二次型。矩阵D=[I]-[S]H[S]为正定的充要条件是其各阶顺序主子式detiD>0。据此,可以分析非理想分束器的相位特性。

2.2 非理想分束器的相位特性

分束器存在损耗时,假定损耗没有破坏分束器的功率互易性,此时ψ1=ψ2但不等于π/2。设ψ1=ψ2=ψ,根据前面的分析,有损耗的分束器传输矩阵可以表示为

图4为插入损耗αs对分束器相位特性的影响,图5为分光比误差ε对分束器相位特性的影响。由式（16)、图4和图5可以看出,当αs为零,即没有损耗时,光纤耦合器的累积耦合相位2ψ=π,与分束器分光比无关;但当考虑插入损耗αs时,累积耦合相位2ψ将大大偏离π相位,且变得与分束器分光比也有关系。尤其在实际中,耦合器插入损耗和分光比误差还随环境如温度、振动变化,对于非互易的光路结构,2ψ与Sagnac相移寄生在一起,将对光纤陀螺的相位检测灵敏度产生严重影响。

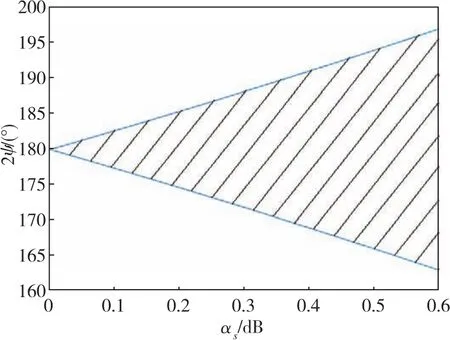
图4 插入损耗αs对分束器相位特性的影响Fig.4 Effect of insertion lossαson phase characteristics of beam splitter

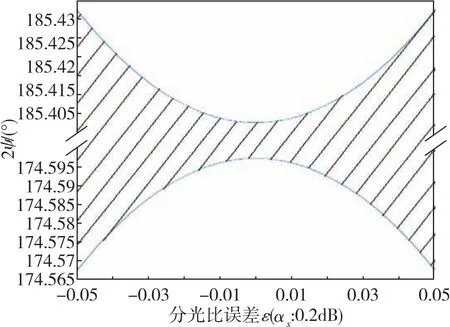
图5 分光比误差ε对分束器相位特性的影响Fig.5 Effect of splitting ratio errorεon phase characteristics of beam splitter

3 输入态对光子纠缠光纤陀螺互易性的影响

非理想分束器传输矩阵SBS取式（12)的形式时,由式（2),非理想Sagnac干涉仪的传输矩阵为

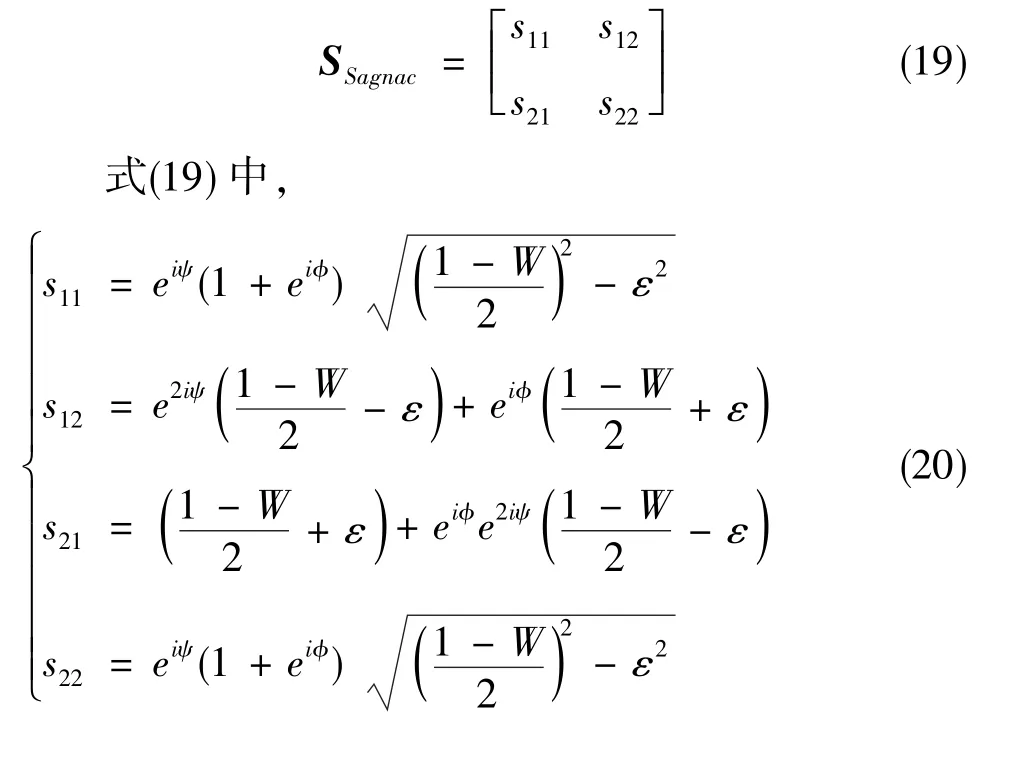
3.1 非对称Fock态输入

当输入态为非对称双模Fock态时,为方便运算,这里以 | 21〉态为例,二阶符合计数为

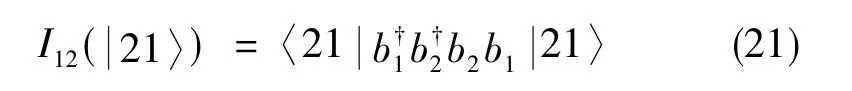
将式（1)、 式（19)、 式（20)代入式（21)中, 并忽略ε的二阶及高阶小量,则有

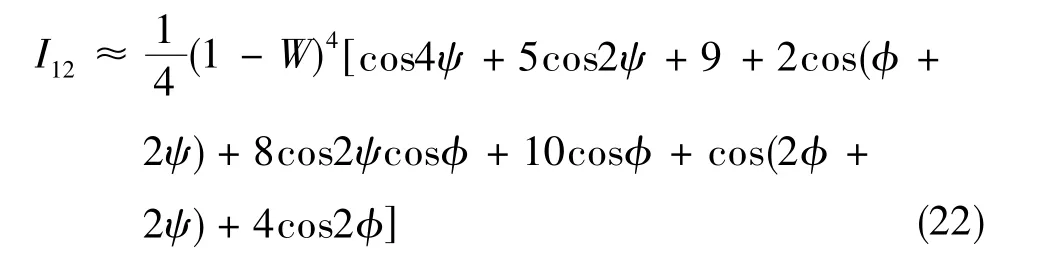
可以看出,非互易误差2ψ寄生在与量子增强项2ϕ有关的余弦项中,与Sagnac相移不可区分。令2ψ =π-δ,可以证明,δ对式（22)中其它项的影响产生了一个二阶强度涨落,可以忽略。考虑偏置相位ϕ→Φ0+ϕ,Φ0=π/4,测量微小ϕ时,只考虑上式中的量子增强项cos（2ϕ +2ψ)+4cos2ϕ,有

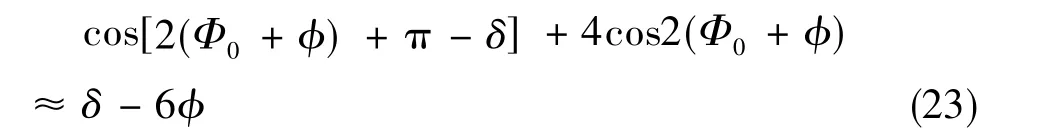
分束器插入损耗和分束器给定,δ是一个固定值,对相位检测没有影响。但分束器常常随环境如温度、振动等变化,致使δ存在不稳定性,进而分束器不理想引起的相位漂移Δϕ为

广义地讲,如果两个端口的输入态是完全不同的量子态,则图2所示也必然是一个非互易性光路,典型例子是相干态+压缩态输入 |α,r〉。其中,α为相干态的振幅,r为压缩态的压缩参数,其二阶符合光强I12中量子增强项为

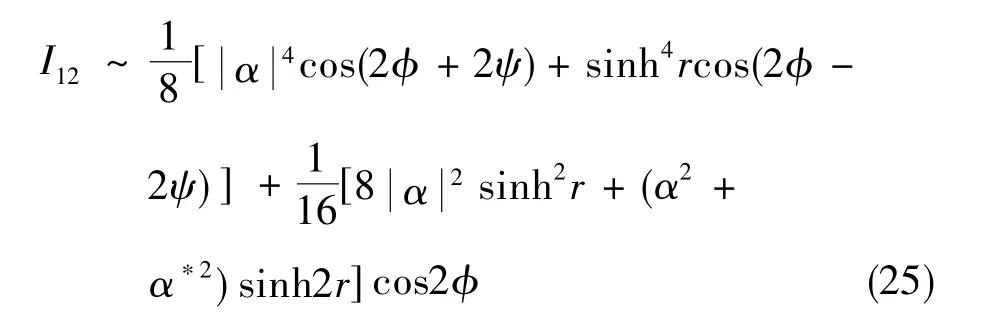
它是δ的一阶小量,不能忽略。因此,对于非对称Fock态输入,光子纠缠Sagnac干涉仪将是一个非互易性光路结构。

在与量子增强项2ϕ有关的余弦项中存在寄生的2ψ相位,显然光路不具有互易性。

3.2 对称Fock态输入

当输入态为对称的双模Fock态时,以 |22〉态为例,二阶符合计数为

可以看出,在与量子增强项2ϕ有关的余弦项中没有寄生的2ψ相位,2ψ只对I12的强度有影响。令2ψ =π-δ,同样考虑偏置相位ϕ→Φ0+ϕ,Φ0=π/4,测量微小ϕ时,分束器不理想引起的相位漂移Δϕ为

这是δ的二阶小量,可以忽略。因此,对于对称的Fock态输入,光子纠缠Sagnac干涉仪将是一个互易性光路结构。

对称Fock态输入的典型光源是双模压缩态,通过参量向下转换（SPDC)产生[9]

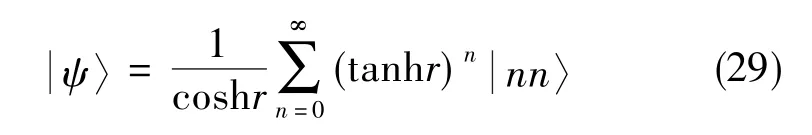
3.3 N00N态

这些都是经过理想分束器产生4004态的输入态,这两种N00N态的输入态都含有非对称Fock态。下面以式（34)为例,研究N00N态的光路互易性。忽略振幅项中与δ2有关的高阶误差项,通过非理想Sagnac干涉仪的二阶相关光强I12为

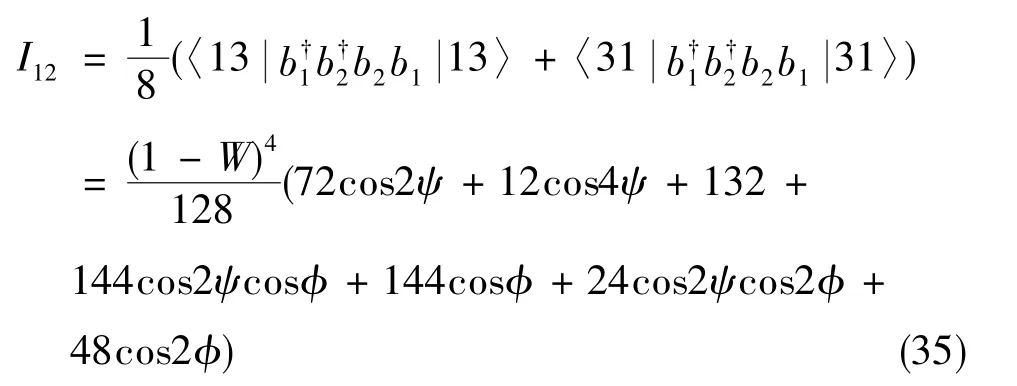
这说明,通过理想分束器后能够生成理想N00N态的输入态组合。在第一次经过Sagnac干涉仪的非理想分束器后,尽管生成的N00N态非理想（含其它态),但第二次经过非理想分束器后,对二阶关联光强I12来说,与量子增强项2ϕ有关的余弦项中不含与2ψ有关的寄生相移。这说明,基于N00N态的光子纠缠光纤陀螺,由于其输入态组合包含等概率形式的非对称Fock态的叠加,理论上仍是一个互易性光路。

4 结论

本文运用散射矩阵模型对非理想光纤耦合器的相位特性进行了理论分析,光纤耦合器耦合光束相对传输光束的相位ψ与光纤耦合器的插入损耗和分光比有关,而插入损耗和分光比随环境（如温度、振动)的变化导致相位ψ存在不稳定性。传统光纤陀螺采用单端输入,输入/输出共享一个端口,确保两束反向传播光波经过光纤耦合器时历经的耦合相移和传输相移相等,从而使干涉信号的固有累加相移抵消为零,这种互易性的光路结构是传统光纤陀螺具有较高相位检测灵敏度的主要原因。本文针对光子纠缠光纤陀螺通常采用双端口输入/输出的结构特征,通过分析不同Fock态输入时的二阶符合计数,对光子纠缠光纤陀螺的光路互易性进行了分析。研究表明,采用对称输入的Fock态（比如双模压缩态),光子纠缠光纤陀螺的双端口输入/输出光路结构仍然具有互易性;但对于非对称的输入态,相位ψ寄生到量子增强的Sagnac相移中,产生一种不能忽略的非互易误差。幸运的是,尽管N00N态的输入态含有非对称Fock态分量,但采用双环行器的非理想Sagnac干涉仪对N00N态来说,仍是一个互易性光路。本文的研究对于光子纠缠光纤陀螺的光源选型具有参考意义。