沉积物可交换态磷量与颗粒物浓度的关系探讨
2022-05-08欧志超高增文
欧志超,高增文,*,程 晨
(1.青岛大学环境科学与工程学院,山东 青岛 266071;2.中国科学院南京地理与湖泊研究所,江苏 南京210008;3.中国科学院大学,北京 100049)
引 言
磷(phosphorus, P)是生物体生长发育和能量传输所必需的营养元素,也是大多数淡水环境和部分近岸海域富营养化的限制性因子[1-3],在水体中的浓度常受到沉积物吸附-解吸作用的调控[4]。在自然水体中,当上覆水磷浓度过低时,沉积物上可交换态磷可被快速解吸到水体中[5],其解吸量与可交换态磷量密切相关;当水体中有过多外源磷输入时,沉积物常表现为吸附磷,这时可交换态磷能够控制沉积物吸附磷的整体行为[6],进而影响沉积物吸附特性的相关参数。此外,可交换态磷量还可用于初步推断沉积物的组成成分(活性铁铝氧化物、有机物等)以及污染历史[7]。因此,确定沉积物在现实环境中的可交换态磷量就显得尤为重要。
研究人员将沉积物原先吸附的可交换态磷称作原有交换态磷(exchangeable phosphate)、本底吸附态磷(native absorbed phosphorus,NAP)或潜在可交换磷[8],虽然叫法有区别,但都表示沉积物在当前状态下已具有的全部可交换态磷量。显然,对于某具体的天然沉积物,其所有的交换态磷含量应是固定的。目前,获得沉积物可交换态磷量的常用方法有提取法和截距法。理论上,沉积物NAP的测定需满足实验溶液的体积无限大且溶液中始终不含磷的理想条件[5],但由于现实实验条件的限制和吸附过程的不完全可逆性,通过提取法和截距法得到结果应表示沉积物在实验环境下的可交换磷量(Q0),而非全部的可交换态磷(NAP);可见,沉积物的NAP与Q0的差异在于:NAP可以表示沉积物在理想状态下能解吸的可交换态磷的总量,Q0表示的是沉积物在真实环境下能解吸出来的部分可交换磷量。因此,确定Q0具有更实际的参考意义。
通过提取法和截距法获取的Q0常随固体浓度(Cs)变化[5, 9],其原因是固体浓度效应的影响。理想情况下,对于给定的天然沉积物,在确定的温度和溶液组成的条件下,沉积物对P的交叉型吸附等温线是唯一的[10]。然而,在实验中通常会观察到偏离这一理想行为的情况,即吸附量(吸附密度)会随着固体浓度的增大而减小(研究人员关注的焦点通常在横轴上方的吸附区),进而导致同一沉积物在不同的固体浓度下都会有与之对应的吸附等温线出现,因此常会引起在每一个固体浓度下的Q0也不相同。关于Q0-Cs的关系,由前述固体浓度效应的分析,解吸的磷量通常也会随着Cs的增大而减小;并且,提取实验结果已表明,Q0-Cs呈负相关关系[5, 11]。但我们发现有的文献中用截距法获取的Q0-Cs却是正相关的关系,这与提取法的结果相矛盾,也与上述固体浓度效应的理论现象相矛盾。
目前,关于Q0-Cs关系的关注与研究较少,本文针对截距法确定Q0时出现的Q0-Cs正相关的矛盾现象,以渤海沉积物为例,进行磷的吸附实验,尝试探讨该矛盾出现的原因,并适当改进截距法。
1 材料和方法
1.1 样品采集与制备
实验用沉积物和海水取自渤海埕岛油田海域(118°19′ E,38°08′ N)。由于该海域的沉积物不易由箱式采泥器获取,改由潜水员采集;将采集的沉积物尽快送回实验室,并置于阴凉处风干,沉积物捣碎、研磨后过100目筛,置于封口袋中密封保存;海水用采水器收集,实验前用0.45 μm滤膜过滤。
1.2 吸附等温实验
在一系列500 mL容量瓶中添加一定量2 mg/L的KH2PO4溶液,再加入上述海水定容,使得其中磷浓度分别接近:0.02、0.05、0.1、0.2、0.3、0.6 mg/L,并采用钼锑抗分光光度法测定具体的磷浓度(初始浓度);准备100 mL离心管若干,分别称取0.1、0.3、0.5 g的沉积物于离心管中,再加入50 mL不同磷浓度的上述溶液,使得固体浓度分别为2、6、10 g/L。每组实验设置三个平行;实验样品在恒温振荡器中恒温(25±1 ℃)震荡24 h[12],取出,离心(转速为5000 r/min),上清液用0.45 μm滤膜过滤,再次测定磷浓度(平衡浓度)。以下列公式计算单位吸附量:
(1)
式中Q为沉积物单位吸附量(mg/g);Ce和C0分别为平衡浓度和初始浓度(mg/L);V是加入离心管中溶液的体积(L);m为沉积物质量(g);Cs为固体浓度(g/L)。
1.3 可交换磷量的计算
之前的研究表明,沉积物与磷作用的热力学宜采用改进的Freundlich经验公式[12]表达,故采用该经验式拟合获取可交换磷量。
在绘制吸附等温曲线时,研究人员对横坐标的选择存在分歧,既有使用C0为横坐标的,又有使用Ce为横坐标的;从总体上看,这两种选择都不会改变吸附曲线的走向,但从细节上来说,横轴的选择至关重要(见下文2.2),本文将对这两种情况进行对比分析。我们在拟合时根据横坐标的不同,将该公式分为两种表达形式:
(2)
(3)
式中,Q、q为沉积物的单位吸附量(mg/g),正值时表示沉积物吸附磷,负值时表示沉积物解吸磷;C0、Ce分别为溶液中的初始磷浓度和吸附实验后的平衡磷浓度(mg/L);Kf、kf为Freundlich吸附平衡常数;N、n为常数,通常小于1。理论上,NAP0、nap0表示实验前沉积物已吸附的全部交换态磷量,是吸附等温图上的纵截距(取绝对值);但是在真实情况下,由于实验条件的限制,计算出来的纵截距只能表示当前实验条件下实际能参与交换的磷量(部分可交换磷量),即Q0(mg/g)。
2 结果与讨论
2.1 横坐标选择对Q0与Cs相关关系的影响
分别以C0和Ce为横坐标绘制吸附等温曲线,用公式(2)、(3)进行拟合,拟合结果见表1。拟合优度R2衡量的是回归方程整体的拟合度,可见F型公式(2)、(3)都较好的拟合了吸附等温数据,且公式(2)拟合情况略优于公式(3)的结果。如图1所示该沉积物吸附等温线为交叉型,横轴上方为吸附区、下方区域为解吸区。在吸附区,无论以C0为横坐标还是以Ce为横坐标,吸附等温线均随固体浓度的升高而下降,说明该沉积物对P的吸附存在明显的固体浓度效应现象[10]。值得注意的是,图1(a)与图1(b)中Q0-Cs的相关关系相反:图1(a)中,以Ce为横坐标拟合出的Q0-Cs是反常正相关关系;而在以C0为横坐标的图1(b)中,Q0-Cs是预期的正相关关系。
在一些相关文献中也出现了Q0-Cs是正相关关系的情况[13-16],尽管这些文献未明确指出该关系,如文献[13]中的图2、文献[16]中的表1,要注意的是他们均是以Ce为横坐标绘制吸附等温线,进而计算得到沉积物可交换磷量。而Koski-Vähälä与Hartikainen在用吸附等温线对重悬沉积物进行风险评估时[9],以C0为横坐标,计算出的Q0-Cs是负相关关系(文献[9]中的表2)。综合以上案例,考虑到获取的实验数据来自同一沉积物,而我们只是在计算Q0时选取了不同的横坐标:选择以C0为横坐标,计算结果Q0-Cs能够符合负相关的关系。因此,我们推测是选取Ce作为横坐标引起了Q0-Cs正相关关系的出现。

图 1 不同固体浓度下吸附量与磷浓度(平衡浓度或初始浓度)的关系(下面的图分别为对应上图的局部放大)
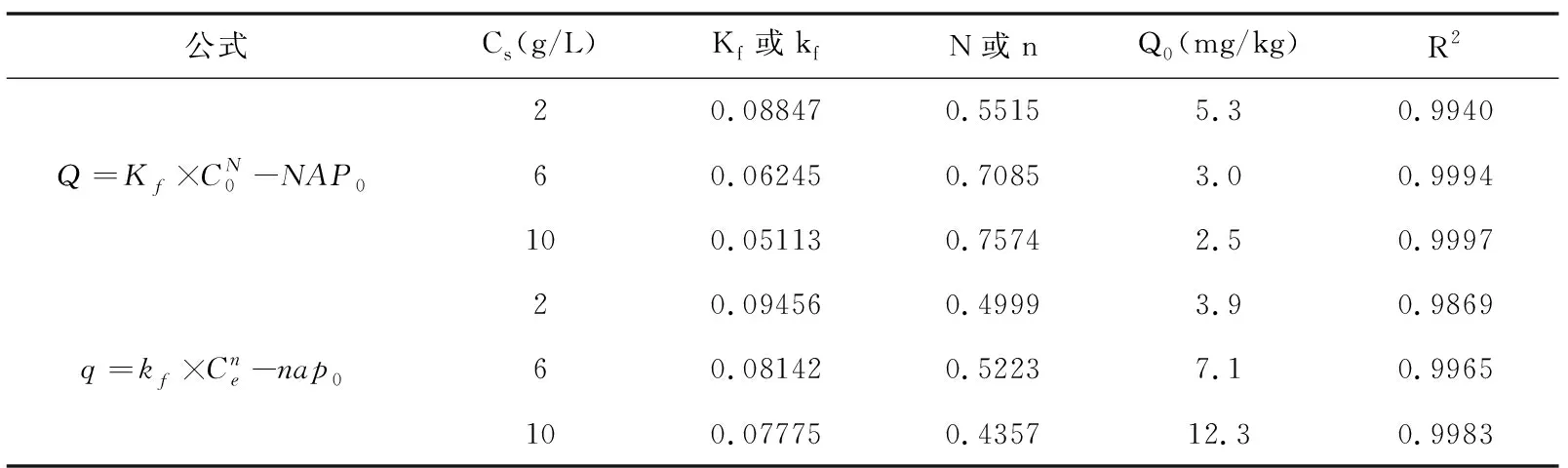
表1 模型拟合优度及吸附参数的拟合结果
2.2 横轴选择影响Q0的潜在原因
从Q0含义的角度解释上述现象:以Ce为横坐标,Q0表示在溶液平衡磷浓度为0 mg/L时,单位质量沉积物解吸出的磷量,这意味着实验需要在无限体积的溶液中进行;这显然与实际相矛盾,因为实验时溶液体积是有限的,沉积物若能解吸出磷,磷的平衡浓度便不可能为0 mg/L;若横坐标选择C0,Q0的物理含义可表示当溶液初始磷浓度为0 mg/L时,单位质量沉积物能够解吸出的磷量,并不涉及平衡磷浓度,这时Q0含义就能明确表达。
提取实验已经证明,Q0-Cs是负相关关系[5, 11]。而固体浓度效应在吸附等温图上的表现是:随着固体浓度的增大,吸附等温线在吸附区的位置越低(单位吸附量越少),但是固体浓度越大,对应的吸附等温线在解吸区的位置应该越高(Q0越小),因此不同固体浓度的吸附等温线在图上应两两相交,促使在交点之下区域改变吸附等温线位置的高低。基于以上讨论,我们观察图1(a):以Ce为横坐标作图得到的吸附等温线可认为是以C0为横坐标得到的吸附等温线的向左拉伸移动,其移动的程度会让各固体浓度下吸附等温线不易在纵轴(y轴)的右侧相交,这导致计算出的Q0与Cs正相关。而在图1(b)中,当以C0为横坐标时各固体浓度下的等温线会在纵轴的右侧相交,这就会出现纵截距Q0-Cs的关系呈现出负相关。关于交点位置的移动影响Q0-Cs的关系是通过观察上述吸附等温线做出的初步推测,其具体原因还有待于进一步探讨。
因此,在利用截距法计算沉积物的Q0时,宜以C0为横坐标。
2.3 Q0-Cs负相关关系的启示
在天然水体中,河床、潮间带和海洋工程区(比如人工鱼礁区)的沉积物在外力作用常发生再悬浮现象[9],再悬浮的强度和持续时间可能对内部磷负荷起决定作用[17]。这是因为再悬浮的沉积物相对于底部沉积物而言其固体浓度是降低的,由于Cs-Q0是负相关关系,再悬浮状态的沉积物的可交换磷的迁移能力会增强(Q0增大),进而提高调控水体磷浓度效率;这与悬浮颗粒物的固体浓度增大,其缓冲能力增强的效应相似[17]。倘若误认为Cs-Q0是正相关关系,将会对水体治理和水质预测产生误导。
Q0可以表征磷在颗粒物-水界面的迁移能力,而Q0随固体浓度的变化则表明沉积物对磷的调控能力与环境条件密切相关。因此,在关于沉积物的吸附特性实验研究中,实验条件的选择应与实际的环境条件尽量相近,这样得到的实验结果能够更好的反映真实情况。此外由于真实环境条件的复杂性,还应适当关注沉积物Q0的变化范围。Q0的范围区间可表现出该区域水体的健康水平与自我调节能力,可为环境决策提供参考。
截距法公式中的纵截距表示为NAP,所以研究人员通常会认为计算出来的纵截距是沉积物全部的可交换磷量,并常会强调该值是被低估的[18]。事实上,用截距法计算出的被低估的“NAP”是沉积物在真实的实验条件下的可以参与交换的磷量Q0。对于某一特定沉积物,Q0会因实验条件的变化而变化;而NAP是一个理论值,是Q0的上限。因此截距法仅适用于直接计算沉积物的Q0;NAP是一个重要的参数,对于获得固液间的分配系数有重要影响。关于NAP的计算,可以使用AMINOT提出的无限稀释外推法(IDE法)[5],IDE法的理论依据之一就是Q0-Cs是负相关关系。在实际水体中,若已知固体浓度的范围,则可通过截距法获得该区域沉积物Q0的范围。
3 结论
(1) 截距法是获取沉积物可交换磷量的重要手段,在使用该方法的过程中,横坐标的选择关系到计算结果的合理性。以C0为横坐标,其对应的Q0的物理含义清晰明确,本文实验结果表明,以C0为横坐标用截距法获得的Q0-Cs是负相关关系,这与文献[11]中提取实验的结果一致;而当以Ce为横坐标用截距法获得的Q0-Cs是正相关关系,这与事实不符。
(2) 通过截距法计算得到的结果是沉积物在实际环境中参与交换的磷量,而非理论上的全部可交换磷量,这是由于理想环境在实验室实验中很难达到。截距法适用于直接计算沉积物的Q0,且宜以C0为横坐标。
(3) 对于固体浓度变化频繁的水环境,如人工鱼礁区,Q0-Cs的负相关关系可帮助了解该局部区域的Q0区间范围,并可为该局部水体的营养健康情况和自我调节能力的评价提供依据。
