微通道内气液两相流中气化率的预测研究

赵晓赋，王 林，杨文韬，张健欣

（内蒙古工业大学自动化系，呼和浩特 010080）

微精馏系统的优点包括使用安全性高、体积小、传质传热的效率高以及易于操控，已经广泛应用于很多领域，其中包括生物医学、有机合成和食品加工等。在微尺度效应的影响下，微通道与常规尺寸的通道相比，两相流型存在很大不同[1]。在微精馏系统中研究最多的、最重要的是微通道内气-液两相流的流动。受不同热边界条件的影响，在微通道内，传热特性对流质的流动有着显著影响[2-3]；微通道内局部热点对流动换热、流型又有很明显的影响[4-5]。在微通道中，改变混合流质的流量对流动及传热特性有显著的影响[6-7]。

顾娟利用微元玻尔兹曼方法，研究了在恒壁温与恒热流2种热边界条件下，稀薄效应对微通道内流质流动、传热特性的影响。微通道内气体受流动特性与稀薄的变化相同，传热特性与稀薄的变化截然相反[2]。KEEPAIBOON 等在水力直径0.68 mm矩形微通道中，在传热方面发现传热系数与流型有一定关系。在低热流范围情况下，传热系数随着饱和温度的变化具有一致性[3]。影响通道内流质的气化率的因素有很多，其中包括气相和液相表观流速的变化和通道壁面加热温度的变化。申利梅等采用VOF（volume of fluid）方法，对局部热点对微通道内压降、换热系数、流型和温度的影响进行了分析[4]。王鑫宝等利用Fluent 软件研究了微通道在滑移区的流动换热情况[5]。刘冬稔和刘肖研究了当微通道内流质的流型为弹状流时，当气相的流量不变时，液相的流量发生改变对流型的影响很小[6]。

本研究建立微通道模型，并利用计算机仿真软件Fluent对其进行求解。在入口流质比例不变的情况下，改变入口流速、管壁加热温度，通过Fluent的后处理计算得到当前工况下流质的气化率。利用最小二乘法，建立流质气化率与流质入口流速、管壁加热温度的多元回归预测模型，并应用其进行不同流速下、不同加热温度下的气化率预测。

1 微通道

1.1 微通道的结构

KANDLIKAR 针对通道内沸腾问题，基于水力直径得出了通道尺度的划分[8]：常规通道（Conventional channels）→3 mm；细通道（Minichannels）→200 μm～3 mm；微通道（Microchannels）→10 μm～200 μm。

本研究建立模型的截面积为800 μm×100 μm，长度为5 mm。水力直径的计算：

式中，R为水力直径，A为过水断面面积，X为过水断面上水流所湿润的边界长度。

将上述条件代入公式(1)得R=44.4 μm，符合微通道的水力直径范围。

1.2 模型入口流速的确定

利用仿真软件Fluent对模型进行求解，模型的入口流速范围是由现场实验设备的流量范围确定的。

实验设备是型号为2PB-10005Ⅲ的平流泵，其体积流量为0.1～100 mL/min。模型的流速范围：

其中：x为换算后模型的流速，S为模型的截面积，y为平流泵的体积流量。

将平流泵的体积流量0.1～100 mL/min、模型的截面积S=0.08 mm2代入式(2)，求得模型的流速为20.84 mm/s～20.83 m/s。因此Fluent 求解器对模型进行求解时，流速范围应当在此范围内。

2 模型的建立与计算

2.1 流体材料的选定

对模型进行流体仿真时，选择液态酒精、气态酒精、液态水和气态水完成气液混合相的确定。流体属性参数如表1所示。

表1 流体属性参数Tab 1 Fluid property parameters

2.2 VOF的参数设置

仿真采用VOF 模型，在模型入口处液态酒精、气态酒精、液态水、气态水的体积比为0.7:0:0.3:0，在出口处测量混合流质的气化率，因此将主相phase-1设置为液态酒精，将phase-2设置为气态酒精，phase-3 设置为液态水，phase-4 设置为气态水。在模型的计算中会发生相变，液态酒精→气态酒精相变温度78.4 ℃，气态水→气态酒精相变温度100 ℃。

2.3 模型和网格

2.3.1 模型的建立

微通道模型的建立采用与现场实验所定制的微流控芯片尺寸一致。因此微通道模型是截面积为800 μm×100 μm，长度为5 mm的管道。

2.3.2 网格的划分

划分后的网格按照网格点之间的相接关系可分为非结构化网格划分和结构化网格划分。结构化网格的网格点之间都是有顺序的并且规则的，此类网格内部各层的网格都要相同的网格数；当几何模型的形状不是很简单时，结构化网格很难划分出符合要求的网格[9]。非结构化网格之间的网格点是无顺序的、不规则的，其划分复杂的结构更为准确，因此选用非结构化网格对微通道模型进行网格划分。

边界层是在高Re绕流中紧贴壁面的粘性力必须考虑的流动薄层。在任何流体域的壁面上都需要设置边界层。在此微通道模型内含有多种气液混合，并且通道内发生液态酒精到气态酒精的相变，为保证结果收敛和计算精度，需要设置边界层，进行局部网格加密[10]。边界层设置情况见图1，边界层数为5。

图1 边界层设置Fig 1 Boundary layer setting

2.3.3 网格无关性检验

在进行数值模拟之前，要先对建立的模型进行网格划分，网格质量和网格的大小对仿真的最终结果起着十分重要作用，后面数值计算结果的准确性直接被其影响。因此对网格的无关性的检验在利用Fluent 软件对模型进行求解时显得尤为重要。

按流质的流速为20.84 mm/s，壁面的加热温度分别设定为99 ℃，时间步长1 ms，对A、B、C、D 4 种网格数进行无关性检验，得到的结果如表2 所示。由表2可知，网格数量对模型气化率结果具有极大影响，当网格超过10 万个时，模拟结果变化差异不大。

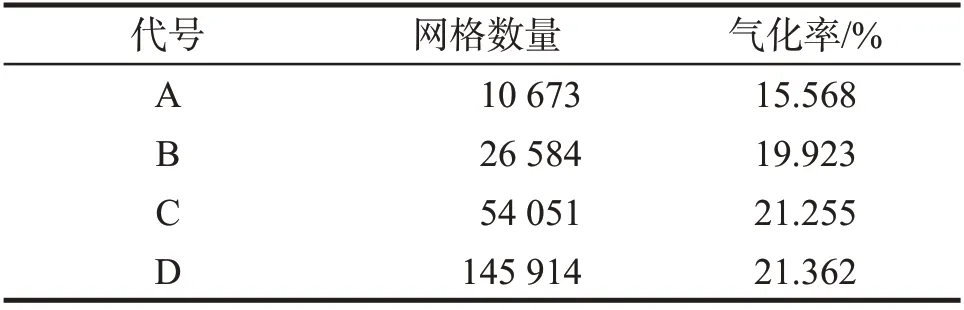
表2 网格无关性检验结果Tab 2 Grid independence test results

结合模型的尺寸，选择合理的网格大小，生成非结构性网格之后，最终得到网格单元总数为54 051。检查划分后所有网格偏度都小于0.8 以下，从而满足计算精度要求。微通道模型的网格划分如图2所示。

图2 模型网格划分Fig 2 Model grid division

2.4 计算模型与边界条件

2.4.1 VOF模型

在液态酒精和水的加热过程中，会产生气态酒精，从而产生两相流的混合问题，Fluent软件中提供了多种多项流模型，其中流体体积（VOF）方法用于捕获多相流交界处中的拓扑变化[11]。

模拟流体的非定常运动的总过程通常采用VOF 方法。在流体域中的每个网格，此函数为混合流质的体积与网格体积的比。对于气-液两相流，气体的体积分数α定义为：

α=单位流体体积/单位体积。(3)

当α=1 时，区域内只有液体；当α=0 时，所定义的区域内只有气体；当0＜α＜1时，区域内气液均存在。

对于VOF 方法跟踪相之间的界面是通过求解连续方程得到的。对于不可压缩的牛顿液体，连续性方程和动量方程及流体运输方程为：

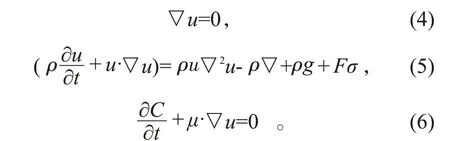
式中，▽为梯度算子；u、ρ、μ、p和g分别为混合流质的速度矢量、密度、黏度、压力和重力加速度。C为流体体积函数，表示网格内混合流质体积与网格体积的比，C=0表示网格内不含目标流体，0＜C＜1表示网格内存在不同的流体，C=1示网格内全部是目标流体。

2.4.2 层流模型

雷诺数（Re）是一个无因次数群，用来判别具有粘性力的流体流动状态。圆管雷诺数的计算：

式中，ρ为混合流质密度，μ为混合流质的动力粘性系数，v为流体域的特征速度，L为特征长度。

当Re＜2 300 时，流动是层流；当Re＞2 300时，流动是湍流；当Re=2 300时，流动是临界流。

对于非圆断面管流，计算雷诺数时需要引入水力直径R，其计算如式(1)所示。代替圆管雷诺数中的特征长度L，经计算本算例的Re＜2 300，因此在模型中流体的流动是层流。

2.4.3 边界条件

模拟中，求解器为压力基求解器，时间为瞬态，由于是微通道模型，因此不考虑重力影响，模型需要对管壁提供连续的热量，开启能量守恒方程。Fluent 的主要边界条件包括入口边界条件、出口边界条件和壁面条件，这些量是一些数学和物理变量。边界条件的设定：采用标准的层流模型方程，速度入口作为入口边界条件，混合流质的流速设置为7 个：2.084、6.25、12.5、18.756、25.0、31.26、37.512 cm/s，入口处温度设置为30 ℃。出口边界为压力出口，出口处温度同样设置为30 ℃。壁面条件的设定：壁面的加热温度分别设定为99～79 ℃间每隔2 ℃。

3 预测模型

3.1 多元回归预测模型

由多个自变量组成的组合{x1，x2…，xn}(n≥2)和因变量y 构成随机样本数据集(x1，x2……，xn，y)，并存在一种如式(8)的线性关系，这种关系通常叫做多元线性回归。

就可以确保模型的预测值最接近实际值[12]。在构建多元非线性回归预测模型的过程中，提高模型预测精度的重要前提是选取契合具体的观测数据的模型函数。

预测模型的精度可以通过回归模型的检验指标实现，主要包括拟合优度检验和显著性检验[13]。

使用判定系数R2作为拟合优度判定模型的拟合优度的主要依据。定义为：

式中，SSR为预测平方和，SST为总离差平方和，SSE为残差平方和。

对预测模型拟合程度的高低，根据判定系数来确定。判定系数越大，预测模型与原始数据越拟合，判定系数越小，说明拟合程度越差，与原始数据偏差更大。R2的取0～1，因此R2越接近于1，模型的拟合效果就越理想。

采用F检验对建立的预测方程进行显著性检验，F统计量定义为：

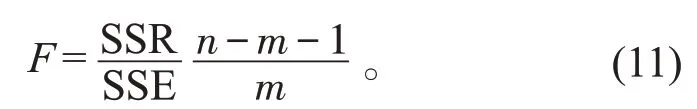
式中，m为自变量个数，n为样本数，F为统计量服从第1自由度m、第2自由度为n-m-1的F分布，即F～(m,n-m-1)。

由F统计量的定义可以得到，当F偏大时，在对因变量造成的变化方面相比，自变量比随机因素的影响大。由此可得，F统计量越大，回归方程的拟合效果也就。

3.2 预测模型的建立

预测模型的建模过程包括数据预处理、建模、分析及预测4大部分，其具体步骤如图3所示。

图3 多元回归流程Fig 3 Multiple regression process

在Fluent 仿真计算中，所得数据共7 组（7 种流速条件），总共77 个样本点（7 种流速×11 个壁面温度），其中1 组数据如表3 所示。其中气化率为出口处气相组分（气态酒精）所占面积与出口截面面积的比。

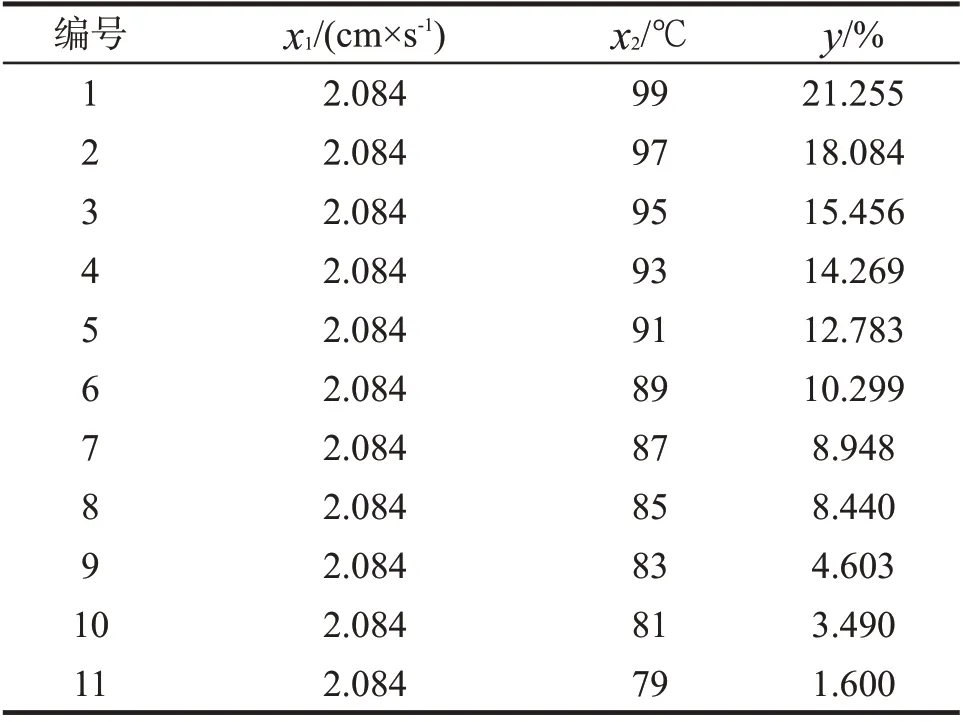
表3 仿真结果（部分）Tab 3 Simulation results(partial)

测量值比预测值之间的差值，通过标准化残差可以明确的表示出来，并且还能得到在绝对值上本次测量的样本点的残差与其他残差之间的差值。当标准化残差的绝对值大于等于某一数值时（在些选择0.5%-线性&0.3%-非线性），表示此残差对应的样本点存在问题。在剔除某样本点后，回归方程的标准差有所下降，即认为此样本点为异常，在拟合时，就对此样本点进行删减。线性和非线性预测模型的残差如图4和图5所示。

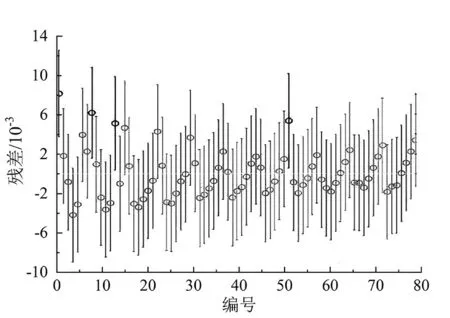
图4 线性回归残差Fig 4 Residual plot of linear regression

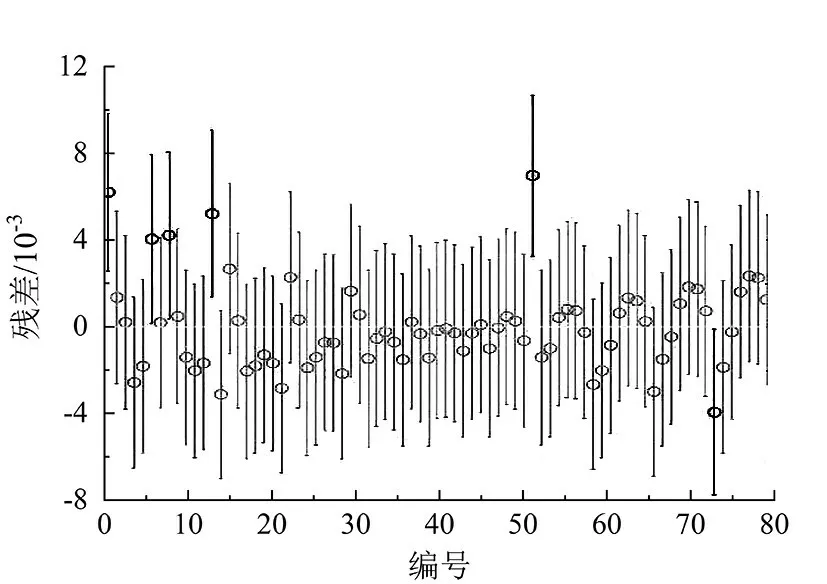
图5 非线性回归残差Fig 5 Residual plot of nonlinear regression

将多元线性预测模型的样本点中第1、8、13、50 个样本点剔除，和多元非线性预测模型的样本点中第1、6、8、13、50、71个样本点剔除后的标准差如表4所示。

表4 剔除异常值前、后的标准差Tab 4 Standard deviation before and after excluding outliers

表5为回归模型拟合检验结果。

表5 回归模型的检验结果Tab 6 Estimated results of the regression model

由表5 可以看出，非线性模型比线性模型在R2统计量上提高了0.178，在F统计量上提高了32.90。

图6为非线性预测方程的三维拟合。

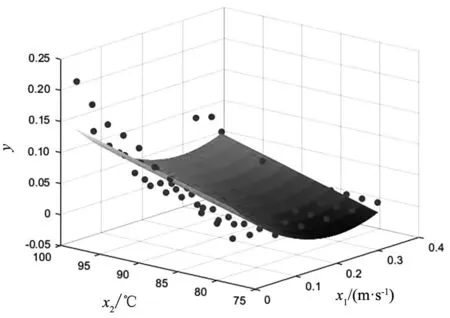
图6 非线性回归模型拟合Fig 6 Fitting graph of nonlinear regression model

综上所述，非线性回归模型拟合结果达到了预期的目标。

3.2 预测模型的应用

为使气化率预测模型对本课题的通用性得到验证，利用预测模型分别在3 种工况下求出气化率，然后与Fluent的计算结果进行比较，结果如表6 所示。考虑到微小截面气相面积分的不精确性，设定的预测精度指标为20%。

由表6 可以看出，3 个仿真模型的气化率误差均低于预测模型精度指标，预测模型的有效性和可行性得到了充分的验证。

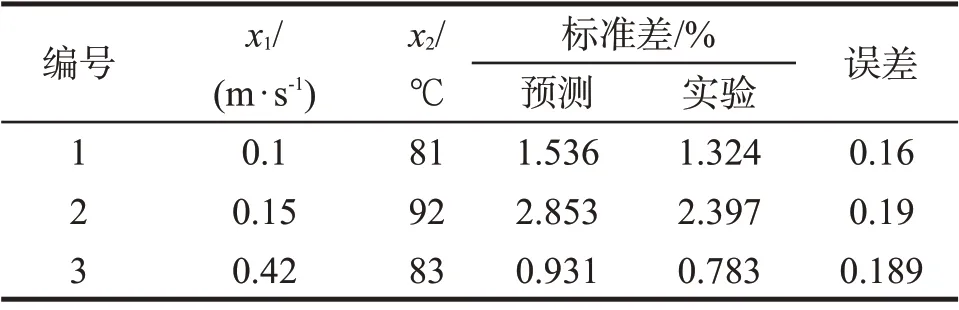
表6 3组仿真结果Tab 6 Three sets of CFD results

4 结 论

通过利用仿真软件Fluent对建立三维微通道模型在不同工况下，对模型出口处的截面混合流质的气化率进行了求解。利用最小二乘法对77 组原始数据处理，建立多元回归预测模型，通过线性预测模型和非线性预测模型的比较，确定了非线性模型结构。利用这个预测模型，对3种独立的入口条件进行了计算。通过和Fluent 的计算结果比较，预测误差均低于20%的预测精度指标。

通过建立入口流速、壁面加热温度与出口气化率之间的关系，可以定量分析两相流的传质传热特性，为构建微精馏系统数学模型做好理论准备。

在下一步的工作中，还将在实验平台上，继续验证预测模型的精度，以期得到实验-仿真-预测模型三者计算结果的统一。