基于改进MF-DFA特征的环形零件缺陷识别

王 幸， 刘文超， 陈文重

(1 湖北工业大学机械工程学院， 湖北 武汉 430068；2 现代制造质量工程湖北省重点实验室， 湖北 武汉 430068)

作为一种高效率、高精度重要检测手段，图像识别技术能够较好地解决机械零件识别中的问题[1-2]。但传统方法只能提取机械零件图像的浅层几何特征，不适用于非线性机械缺陷识别问题。而多重分形作为单分形的延伸与拓展，相比较于单一分形能够更精确和细致地刻画非线性机械零件的全局和局部特征信息。多重分形去趋势波动分析算法(multifractality detrended fluctuation analysis，MF-DFA)是一种将去趋势波动分析与多重分形法相结合的方法[3-4]。林近山[5]利用MF-DFA算法计算得到齿轮箱故障信号的多重分形谱的奇异值，以提取不同故障情况下的特征，用于诊断正常、轻微磨损、中度磨损与断齿情况下的齿轮箱的故障。赖科学[6]使用分形理论中的分形维数(FD)对同步器齿环零件进行了缺陷识别的研究，通过利用结构函数法计算正常与缺陷齿环内轮廓展开曲线的分形维数，根据所得维数的差异完成对正常和缺陷齿环的准确识别。余坤[7]利用三角形盒子法计算齿环、齿轮、螺钉和螺母等零件图像的多重分形谱，从而获得这4类零件图像多重分形谱的特征值，并设计贝叶斯分类器实现正常与缺陷齿环零件的识别。豆永坤[8]关注于硬件的选型、视觉系统的设计、相关算法的研究以及相机标定等方面，设计了机器视觉技术的检测平台，并据此分析研究机械零件的外形缺陷检测、垂直度、同轴度以及零件的平行度，对所选取合适的对象进行检测，以满足齿轮轮齿缺陷检测的需求。朱霞[9]针对不规则零件尺寸检测出现的问题以及该零件表面缺陷检测等进行了研究，构建了检测无规则卡箍缺损的硬件平台，并且针对机器视觉的不规则卡箍检测的软件系统进行了探索开发。在前人研究的基础上，本文提出一种改进的MF-DFA算法，通过联合滑动窗口、经验模态分解(empirical mode decomposition, EMD)与三角覆盖模型，不仅可检测长程相关性确定分形结构特征，而且还能判断时间序列是否具有多重分形属性[10]。

1 基于滑动窗口与EMD的三角旋转覆盖MF-DFA

根据EMD的计算步骤，从原始信号中逐次分解出n个imf和一个残余分量rn(t)，余项就是消除趋势波动项，代替最小二乘多项式拟合消除趋势波动后的残差序列yv(i)，进而得到波动项，然后将该波动项分成几个部分，按照不同的q值，计算信号的波动函数Fq(s)，求取Fq(s)与q的对数最小二乘拟合斜率，就可以得到信号的广义Hurst指数。

滑动窗口不会丢失尾部数据，不需要把原始数据进行倒置重复一次，以免影响多重分形分析结果的客观性。本文选取的滑动窗口步长为1。对同一条不规则且具有一定自相似的轮廓曲线分别用正方形模块(图1a)和三角形模块(图1b)进行覆盖。在部分正方形模块中，图形轮廓实际只占据正方形模块区域很小一部分，但计算时仍算作是一格。由于图形面积是按占据模块的面积来计算，因此正方形模块覆盖会导致对图像的过度覆盖，使计算结果出现较大误差。而三角形覆盖方法在保证图像完全覆盖的情况下，解决了过度覆盖的问题，提高了图像覆盖的精度。故本文利用滑动窗口技术、EMD与三角旋转覆盖模型对传统MF-DFA算法进行改进。

图 1 覆盖轮廓曲线图

基于滑动窗口技术和EMD的三角旋转覆盖MF-DFA算法的具体计算步骤如下。

1)对一幅大小为M×N的图像x(m,n)构造去均值和序列R(i,j):

(1)

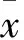
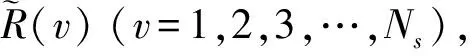
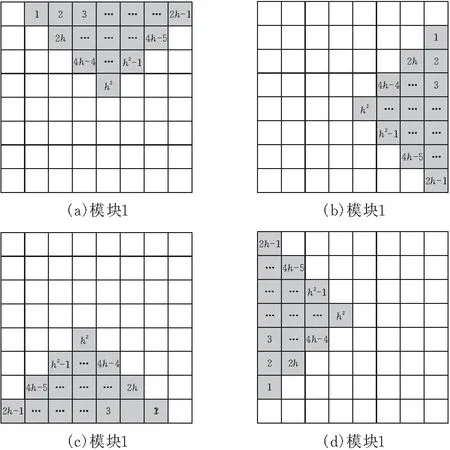
图 2 三角形覆盖轮廓曲线图像

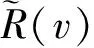
(2)

4)计算均方误差

(3)

5)对于N-s+1个区间，求F2(s,v)的均值，并计算q阶波动函数Fq(s)

(4)

6)重复第5)步，不断改变等腰三角形模块的高h，获得一组不同尺度h下的测度波动函数Fq(s)，对s和Fq(s)取对数得到log(s)和log(Fq(s))。将两者进行线性拟合得到h(q)，计算奇异指数α、奇异谱f(α)得到图像多重分形谱。

2 零件图像的缺陷特征提取与分析

为实现轴承的缺陷识别，以常用的轴承零件为研究对象，利用改进MF-DFA算法计算轴承零件图像的多重分形谱，提取其多重分形谱中特征值。通过分析零件非线性特征，从非线性特征中找出可作为缺陷识别的特征值，在智能识别领域显得非常有必要。本文选用如图3所示的轴承进行实验，每张图像的像素大小为512×512。

图 3 正常与缺陷轴承零件图像

使用改进MF-DFA算法对图3所示的轴承零件图像进行广义Hurst指数h(q)计算，其中q的选值范围为-15～+15，取值间隔为0.18，计算结果如图4所示。可以观察到轴承零件图像的h(q)均随着q值的改变而显著变化着。因此轴承零件具有多重分形特性，可以使用多重分形谱对其进行特征分析。

图 4 正常与缺陷轴承图像的广义Hurst指数h(q)

利用改进MF-DFA算法对图4所示的正常与缺陷轴承零件图像进行多重分形谱的计算，计算结果如图5和图6所示。其中图像的多重分形谱上有167个点，每个点的横坐标为奇异指数α，每个点的纵坐标为奇异谱f(α)。单张零件图像的多重分形谱无法完美诠释零件图像的整体特征，因此采集各20张正常与缺陷轴承零件图像，并计算其多重分形谱，从中分析并提取出最具代表性的特征值。图5a为其中编号为1的正常轴承图像的多重分形谱，图6b为其中编号为1的缺陷轴承图像的多重分形谱。

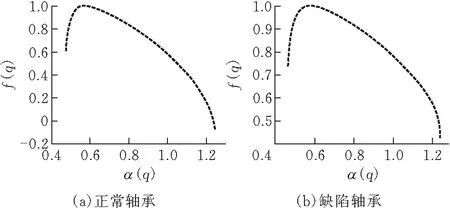
图 5 编号1图像多重分形谱

零件图像缺陷特征的数据资源来自正常与缺陷各20张轴承图像，每张图像均有167个数据。因此轴承零件缺陷特征数据可以组成一个大小为40×167的矩阵A1。A1的每行数据均为一张轴承零件图像的缺陷特征数据，其中第1～20行为正常轴承图像的缺陷特征数据；第21～40行为缺陷轴承图像的缺陷特征数据。本文选用的降维方法为核主成分分析(kernelized principal component analysis,KPCA)[11]，将A1作为样本数据集进行降维处理，可提取出轴承零件的缺陷特征值，经过后A1特征值的累计贡献率如图8所示。

图 6 A1特征值的累计贡献率

根据图6可知。A1在其第二个特征值处的累计贡献率Bi超过了0.95，因此A1被降维后，每个样本(即每张图像)均具有2个主成成分特征值——λ31与λ32。最终轴承零件缺陷特征值Y1是一个大小为40×2的矩阵。将每张图像的2个主成成分特征值作为每个二维空间点的位置坐标，以二维图像的方式将Y1展示在图7中。如图7所示，数据点组成的2个群簇分别代表正常与缺陷轴承的零件图像，表明零件图像缺陷特征提取成功。

图 7 轴承零件图像缺陷特征值

3 基于LS-SVM的零件图像缺陷识别

获得了较为精确的轴承零件图像缺陷特征值，接下来的工作便是进行轴承零件的缺陷识别。在众多识别方法中，由于最小支持向量机(least squares support vector machines, LS-SVM)[12]把 SVM 中的不等式约束变为等会约束，把偏差的一次方求解变为二次方，很大程度上方便了拉格朗日乘子 alpha 的求解，并且将二次规划问题转化为利用最小二乘法求解线性方程组的问题，加快了计算求解速度。因此本文选择的识别方法为LS-SVM。

3.1 零件图像缺陷识别数据准备

3.1.1零件图像缺陷识别训练集与测试集获取轴承图像缺陷特征值Y1，Y1是一个大小为40×2的矩阵，来自各20张正常与缺陷轴承，Y1的每行数据均为每张轴承零件图像的缺陷特征值。先对轴承零件图像缺陷识别训练集与测试集进行获取与格式调整，因此需将Y1转化为轴承图像的缺陷识别训练集与测试集。具体工作如下：为使得训练数据集均衡，从Y1里的正常与缺陷轴承零件各20张图像缺陷特征值中各随机抽取10张图像的缺陷特征值，将它们整合后作为轴承缺陷训练数据集D3。其余轴承的正常与缺陷零件10张图像的特征值则整合后作为轴承图像缺陷测试数据集E3。D3与E3均是大小为20×2的矩阵。随后，根据LS-SVM的标准调整D3、E3的格式，将它们依次归一化，得到轴承图像的缺陷标准训练集train_chq2，以及轴承图像的缺陷标准测试集test_chq3，train_chq3与test_chq3均是大小为20×2的矩阵。由于D3、E3、train_chq3与test_chq3的数据量较大，本文将每张轴承图像的缺陷特征值作为每个二维空间点的位置坐标，D3、E3、train_chq3与test_chq3如图8与图9中可视化显示。

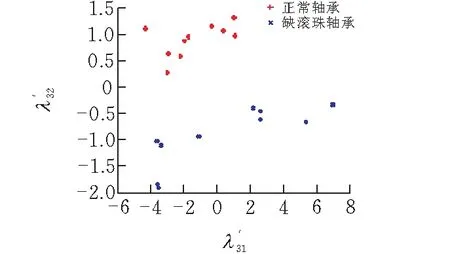
(a)轴承图像缺陷训练数据集D3

(b)轴承图像缺陷测试数据集E3图 8 轴承零件缺陷训练与测试数据集

(a)train_chq3

(b)test_chq3图 9 轴承图像缺陷标准训练集与测试集

3.1.2轴承缺陷识别Lib-SVM最佳参数选择获取轴承图像的缺陷标准训练集train_chq3后，需将其进行交叉验证以获取轴承图像缺陷识别的最佳参数。具体工作为，在2-7～27内分别多次改变 ，并且将其对应的train_chq3中20张轴承图像的数据各随机分成4个数据量相同的部分，轮流将train_chq3中的每一个部分作为轴承图像测试集进行预测，train_chq3其他3个部分作为轴承图像训练集对LS-SVM进行训练，分别计算train_chq3这4个部分轴承缺陷识别准确率的平均数p3，取使p3最大的参数为轴承图像缺陷识别最佳参数。交叉验证结果如图10所示，其中的线条代表p3的等高线，每条线上的数值均为p3的100倍。本次测试p3的最大值为100%，且有多组数值不同的(c3,g3)可以使得p3取得最大值。由于惩罚参数c3过高时会造成过学习状态，因此选择惩罚参数c3最小的一组参数作为最佳参数。本次最佳参数(c3,g3)的取值分别为c3=0.0078125，g3=0.5。

图10 最佳参数(c3,g3)交叉验证结果

3.2 零件图像缺陷识别预测结果

将轴承图像最佳缺陷识别参数与train_chq3带入LS-SVM中的训练函数(svmtrain)进行训练，可获得轴承图像缺陷识别SVM模型model3。随后将model3、test_chq3，带入LS-SVM中的模型测试函数(svmpredict)进行运算，即可获得轴承图像缺陷识别预测结果。轴承图像缺陷识别预测准确率Accuracy3为100%，标志着本次轴承图像缺陷识别成功。如图11所示，test_chq3中20张正常与缺陷轴承图像的特征值全部被准确识别预测。

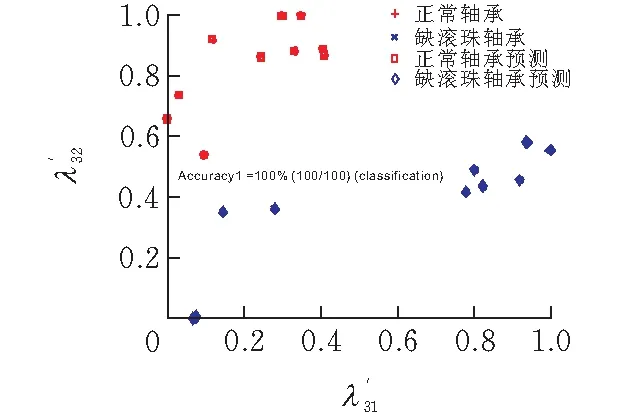
图11 轴承图像缺陷识别预测结果

4 结束语

本文使用改进MF-DFA算法描述机械零件图像的属性特征，用于零件图像的特征提取与缺陷识别。利用滑动窗口技术方法对目标序列进行分割，再利用EMD方法代替基于最小二乘原理的多项式拟合计算去趋势函数，通过三角旋转覆盖模块替代传统MF-DFA算法的正方形覆盖，提出一种基于滑动窗口技术、EMD和三角旋转覆盖模型的改进MF-DFA算法。使用改进MF-DFA算法计算轴承图像的多重分形谱，针对特征资源数据量过大，维数较高的问题，将其降维，得到数据量少而精的轴承零件图像缺陷特征值。选用LS-SVM作为零件图像缺陷识别方法，将轴承零件图像缺陷特征值转化为零件图像缺陷训练集与测试集，获得零件图像缺陷识别结果。结果表明，轴承零件图像缺陷识别准确率高，特征鲁棒性好，能有效识别缺陷零件图像。