爆破振动下露天矿台阶边坡的稳定性分析

肖 雨， 汤 华， 邓 琴， 翟会超

(1 湖北工业大学土木建筑与环境学院， 湖北 武汉 430068； 2 中国科学院 武汉岩土力学研究所， 湖北 武汉 430071；3 云南黄金矿业集团股份有限公司， 云南 昆明 650000)

保障矿山边坡的稳定性是露天矿山开采中最重要的工作。随着我国经济建设的快速发展，对矿产资源的需求也日益增加，保障露天矿山在开采过程中边坡的稳定性就是保障了矿山的生产效率。平面滑动是露天矿岩体边坡中常见的一种破坏形式，对此国内外已做了很多相关研究[1-6]。典型岩质边坡的平面滑动破坏通常是滑体沿与山坡倾向大致相近的单一滑面滑移，其稳定性在很大程度上由岩体中的控制性结构面决定。

影响露天矿山边坡稳定性的因素有很多，除了受到地质、岩体等自然条件影响外，还受到采矿工程活动的影响，如爆破震动[7-8]。爆破作业是露天矿山的生产开采中的日常工作，岩体结构在频繁地受到爆破震动的影响下势必会产生裂隙，对此如果没有控制管理措施，将会导致台阶发生局部破坏从而影响到正常的生产作业。因此保证露天矿山的台阶边坡在爆破震动的影响下的稳定性是不容忽视的。

时卫民等[9]对阶梯形边坡的稳定性进行了研究，通过静力平衡方程解得边坡稳定系数的解析解，得到了阶梯形边坡的简化计算公式。该公式具有计算快速简便的特点，但仅考虑了边坡的自重因素，未考虑其他外来因素对边坡稳定性的影响。缪世贤等[10]考虑地震对边坡的影响，改进得到了台阶边坡平面滑动破坏时安全系数的公式，并分析了台阶坡高、滑面倾角、边坡角等因素与安全系数之间的关系，其所求得的关系式不方便工作人员对边坡稳定系数快速求解的需求。蒋斌松等[11]对折线和台阶形边坡、边坡出现张裂缝和静水压力的情况、考虑地震力的影响，对这几种类型边坡进行了分析，得到了可以求解出边坡最不利滑面和最小安全系数的解析算式，但是该解析解中各参数对边坡稳定系数的具体影响，作者没有进行分析。类似方面的研究如，文献[12]按照毕肖普法推导出爆破振动下顺层边坡稳定系数的计算公式，说明了爆破振动拟静力系数和顺层边坡安全系数的关系[12]。文献[13]对边坡在水力作用下滑面的极限倾角进行了解析解的推导，并根据建立的解析解，编写了计算程序[13]。以上研究均未看到爆破荷载作用下多台阶边坡的滑面倾角的解析解。

本文依托于云南省北衙万硐山矿段露天金矿开采工程，对该露天金矿开展了台阶边坡稳定性分析工作，考虑爆破振动力的影响，求解边坡发生平面滑动时最危险滑面倾角和最小稳定系数的解析解，并对主要参数进行了敏感性分析，为露天矿山台阶边坡的设计提供了参考，结合实际工程应用证实了该公式的正确性和适用性。

1 台阶边坡稳定性分析

按照《非煤露天矿边坡工程技术规范》(GB51016-2014)中5.2.5所示，爆破振动力荷载可采用拟静力法，并可按规范的规定取值。本文在运用极限平衡法对受爆破影响的矿山台阶边坡进行稳定性分析时，考虑到爆破振动力是一种变化的动力荷载，为了简便计算，将爆破振动力拟静力化对矿山台阶边坡的稳定性进行分析。

1.1 单阶边坡的稳定性分析

如图1所示，假定边坡滑面为直线，已知θ为边坡滑面倾角，α1为台阶边坡坡角，l和k分别是滑面长度和台阶坡高，γ是岩体重度，c和φ分别是粘聚力和内摩擦角。

图 1 单阶边坡计算模型

根据边坡稳定系数的定义和力的平衡条件，考虑爆破影响下边坡的稳定系数

(1)

式中:B为爆破等效静力;B=β0k0G。为方便计算，令k=β0k0，定义k为计算折减系数。

根据三角形正弦定理求得滑体重量

(2)

为了方便计算求解出解析解，引入滑面水平投影距离x，则可得出以下几何关系式：

将上述几何关系式代入式(2)，得滑体重量

(3)

将式(3)和几何关系式代入式(1)，得

(4)

(5)

对式(5)求导，并令其导数等于零，得

化简得

(h+k2h+C1-C1kcotα1)x2- (2C1kh+2C1hcotα1+2h2cotα1+2k2h2cotα1)x+ (h3cot2α1+k2h3cot2α1+C1kh2cotα1-C1h2)=0

解上述方程得

由图1的几何关系可知当x≤hcotα1时，滑面会出现在台阶边坡外，这不符合常理，因此方程所求解为

(6)

因此所求解式(6)就是单阶边坡最不利滑面的水平投影距离，将其代入式(4)即可求出单阶边坡最不利滑面的稳定系数，这个稳定系数也就是台阶边坡的最小稳定系数。同时根据几何关系θ=arctan(h/x)，可以求出单阶边坡最不利滑面的倾角θ。

1.2 二阶边坡的稳定性分析

已知a1是台阶平面宽度，k1和k2分别是两阶边坡的坡高，α1和α2分别是两阶边坡的坡角。根据几何关系可得三角形ABC的重量

(7)

四边形BDEF的重量

(8)

为了求解方便，令

得

则滑体重量G为三角形ABC的重量G1减去四边形BDEF的重量G2，即

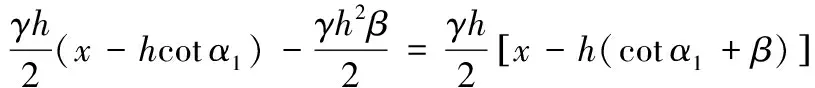
(9)

将式(9)和几何关系式代入到式(1)中，得

(10)

(11)

对式(11)求导，并令其导数等于零，获得方程求解：

±

同理从图2中可以看出，当x≤hcot (α1+β)时，滑面会出现在台阶边坡外，这不符合常理，因此方程所求解为

(12)

式中

式(12)就是二阶边坡最不利滑面的水平投影距离，将其代入式(10)即可求出二阶边坡最不利滑面的稳定系数，这个稳定系数也就是二阶边坡的最小稳定系数。同时根据几何关系θ=arctan(h/x)，可以求出二阶边坡最不利滑面的倾角θ。

图 2 两阶边坡计算模型

1.3 多阶边坡的稳定性分析

通过对比式(12)和式(6)不难发现，求解出的二阶边坡最不利滑面的水平投影距离的解析解和单阶边坡的解析解相比，只是cotα1换成了cotα1+β。通过推导过程也可以知道，β与边坡滑体的重量G相关，只需要推导出多阶边坡滑体的重量G的规律公式，即能够求得β的值，由此就可以推导出多阶边坡的解析解。

对于露天矿山台阶边坡而言，为了便于施工生产，一般情况下各级台阶边坡的结构参数相同，即台阶边坡的平台宽度a1=a2=…=an=a，台阶边坡角α1=α2=…=αn=α，台阶高度k1=k2=…=kn=k/n。

所以对二阶边坡而言，易得

(13)

由图3易得，滑体重量为三角形ABC的重量减去四边形DEFJ和四边形JHIB的重量，即

(14)

式(13)联立式(9)可解得

(15)

图 3 三阶边坡计算模型

由图4易得，滑体重量为三角形ABC的重量减去阴影部分的重量，即

(16)

图 4 四阶边坡计算模型

同样联立式(9)，可解得

(17)

比较式(13)、(15)、(17)，当台阶边坡有n阶时，β的值为

(18)

在求解时，将β值代入式(12)中即可求解出多阶边坡最不利滑面的水平投影距离，继而求解出最不利滑面的倾角θ和最不利滑面的稳定系数F。

2 敏感性分析

上述所求的解析解中含有大量的岩体力学参数和台阶边坡结构参数，为了针对性的对边坡稳定性问题提出优化解决方案，需要对这些参数进行敏感性分析。根据大量的文献调研和现场勘察，选取五个参数进行敏感性分析，分别是台阶高度、平台宽度、坡面角、粘聚力、内摩擦角。

2.1 计算结果

某露天矿山北帮边坡[14]的参数分别是：台阶高度12 m，平台宽度10 m，坡面角65°，粘聚力200 kPa，内摩擦角36°。根据该矿以往爆破试验取得计算系数k值为0.012。以该露天矿山的三台阶边坡为例，按偏离度-20%，-10%，0，10%，20%作为敏感度计算的参数域，见表1。

表1 参数敏感度计算取值表

采用控制变量法将各个参数取值代入式(12)计算边坡的稳定系数，最终得到在爆破振动下各因素对边坡的稳定系数的影响(图5-图9)。为了更加准确地得到五个参数对稳定系数的敏感度，定义无量纲形式的敏感度函数[15]：

(19)

式中：Si(λi)为λi对P的敏感度，λi为第i个影响因素，ΔP是系统特性的差值，P是基准状态下的系统特性，Δλi是影响因素的差值，λi是基准状态下影响因素的值。

按上式计算得到爆破振动下五个影响因素对稳定系数的敏感度如表2所示。

表2 结构参数和力学参数对稳定系数的敏感度

2.2 数据分析

从图5中可以看出，增加台阶高度会导致边坡稳定系数明显减小，台阶高度9.6 m时稳定系数最大，台阶高度14.4 m时稳定系数最小，稳定系数的减小幅度为33.71%。从图6中可以看出，随着平台宽度的增大，边坡的稳定系数缓慢增加，在平台宽度8 m时，边坡的稳定系数最小为3.22，在平台宽度为12 m时，边坡的稳定系数最大为3.77，稳定系数的增加幅度为16.80%，增加幅度不明显。从图7中可以看出，在台阶坡面角为52°时，稳定系数最大为4.28，随着台阶坡面角的逐渐增大，边坡的稳定系数显著减小，当坡面角增大到78°时，稳定系数减小到2.89，此时稳定性数最小，稳定系数的减小幅度为32.47%。如图8和图9所示，随着岩体的粘聚力和内摩擦角逐渐增大，边坡的稳定系数也在增大，在粘聚力的变化影响下稳定系数增加幅度为28.10%，在内摩擦角的变化影响下稳定系数的增加幅度为22.78%，稳定系数增加都比较明显。

图 5 台阶高度对稳定系数的影响

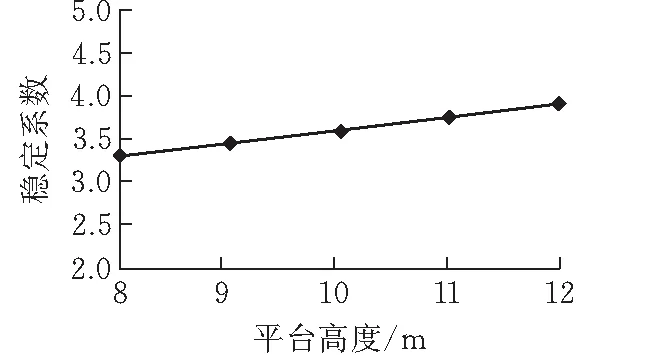
图 6 平台宽度对稳定系数的影响

图 7 坡面角对稳定系数的影响

图 8 粘聚力对稳定系数的影响

图 9 内摩擦角对稳定系数的影响

从图5-图9的数据分析中可知，边坡的岩体物理力学参数和台阶结构参数的变化均会对露天矿山边坡的稳定系数产生影响，但总体来说，台阶结构参数对露天矿山边坡稳定性的影响大于岩体物理力学参数对露矿山边坡稳定性的影响。结合表2所示的各参数对稳定系数的敏感度能更加准确的看出，在爆破振动下对露天矿山边坡稳定系数影响最大的因素是台阶高度，影响最小的因素是平台宽度，各因素对稳定系数影响程度由大至小分别是台阶高度>坡面角>粘聚力>内摩擦角>平台宽度。

3 工程应用

云南省鹤庆北衙万硐山矿段位于滇西北鹤庆县城南部172°方向，露天矿采场边坡以灰岩为主。以南西侧矿山边坡为研究对象，根据工程地质调查报告结构面的统计数据显示，如图10所示，在北衙露天金矿南西侧区域一共统计了15处共计31组结构面，其中包括6组层理和25组节理。层理与坡面反倾，大部分倾角小于30°。节理发育有一组顺倾30°的节理。

根据现场爆破方案，得爆破计算系数k=0.061。台阶高度为15 m，台阶坡面角为70°，安全平台宽度设置为4 m。根据现场开展的原位直剪试验，灰岩粘聚力取值为200 kPa，内摩擦角为39°，岩体容重为26.9 kN/m3，如表3所示。

图10 矿区南西区结构面统计图

表3 结构参数和力学参数取值表

采用上述解析公式得到3台阶边坡最不利滑面倾角θ为40.06°，稳定系数为2.00；4台阶边坡最不利滑面倾角为41.03°，稳定系数为1.74；5台阶边坡最不利滑面倾角为41.89°，稳定系数为1.57。这些最不利滑面的稳定系数均大于《非煤露天矿边坡工程技术规范》(GB51016-2014)中表3.0.9所示设计安全系数，这说明现状边坡的稳定性是满足规范要求的。

然而，需要注意的是，边坡最不利滑面倾角和爆破系数有直接的关系。上述稳定性是建立在现有爆破设计方案的基础上，随着采矿作业的深入，在今后的爆破作业施工中需要关注爆破方案的变更可能会引起优势节理面发生破坏，引起局部台阶边坡发生失稳破坏，进而影响施工生产。

因此，在今后的开采爆破施工作业中，应该根据边坡已有层理弱面形状、方位、倾向先查明滑面位置，判定产生滑动的岩体部位，根据可能允许影响的程度确定爆破规模，调整爆破参数和装药结构并采取其它有效技术措施，以避免爆破振动直接诱发台阶边坡的破坏。

4 结论

台阶边坡的平面滑动破坏是露天矿边坡局部破坏的主要形式。本文在考虑爆破的影响下推导了平面滑动下最不利滑面的倾角，开展了影响因素的敏感性分析，并应用于北衙露天矿边坡，得到如下结论：

1)建立考虑爆破振动影响下多台阶边坡计算模型，推导出了多台阶露天矿山边坡发生平面滑动最不利滑面倾角的解析解。

2)对爆破振动下多台阶露天矿山稳定影响最大的因素是台阶高度，其次分别是坡面角、粘聚力、内摩擦角、平台宽度。随着台阶高度和坡面角的增加，边坡的稳定系数单调递减，随着粘聚力、内摩擦角和平台宽度的增大，边坡的稳定系数单调递增。

3)在云南北衙金矿工程实践应用中，对矿区南西侧多台阶边坡求解，得到最不利滑面倾角在40°左右，说明台阶边坡当前稳定性较好，但在今后的爆破作业中需要注意爆破炸药的使用量，避免因为炸药用量的加大直接诱发局部台阶边坡的破坏。