改进的小波包双参数双阈值降噪方法

李伟 李林

（铜陵学院，安徽 铜陵 244061）

一、引 言

在现代电子测量和传感测试领域中，采集到的数据经常无法避免地被各种噪声所干扰。为了提高特征提取的准确度，对采集到的数据进行降噪处理是很有必要的。小波包变换是一种具有时频域、多分辨率等特性的信号处理方法，非常适合用于消除非平稳噪声。目前基于小波包变换的降噪方法包括模极大值法、空域相关滤波法和阈值法等。其中，小波包阈值降噪法理论简单、可实行性高且在工业现场被广泛应用。

从提出到现在，已有许多学者对小波阈值去噪法做了深入的研究，其中最为经典的是Donoho等[1]提出的软、硬阈值函数去噪法。虽然这两个函数具有一定的去噪效果，但也存在许多不足之处。针对其不足，国内外很多学者相继提出了一些改进的阈值去噪函数[2-3]。这些函数虽然在一定程度上兼顾了软硬阈值函数的特点，但也存在一些如函数阈值选取相对固定、函数缺乏灵活性等不足。针对上述问题，文献[4]提出了一种小波双阈值双因子函数。该函数通过引入双阈值和可变因子，使其能通过改变参数值来调节降噪幅度。但研究发现，该阈值函数不能根据实际信号中的噪声能量分布来局部调整降噪程度，从而导致降噪效果不太理想。本文丢掉可变因子，引入新的调节参数和函数模型，以期改进后的阈值函数能够根据实际信号中有用信号和噪声信号的分布来整体和局部的调整函数的降噪幅度。改进后的阈值函数亦连续且抑制了恒定偏差。最后通过仿真和实验信号，比较不同小波阈值去噪法的信噪比和均方误差，验证本文方法的有效性。

二、传统与现有阈值降噪方法

w是原始信号小波包分解后的系数，T是阈值，η(w)是阈值函数处理后的小波包系数。

(一)传统双阈值法

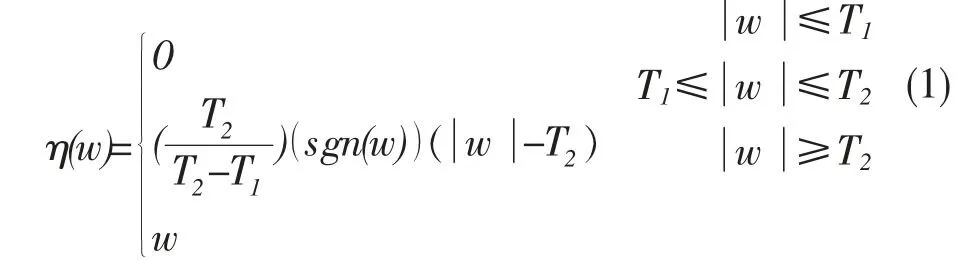
传统双阈值函数克服了函数不连续的问题，并有效地抑制了处理后小波包系数之间的恒定偏差。但该方法对大于上阈值的部分不做任何处理，可能导致去噪不干净的情况发生。

(二)文献[4]的阈值法

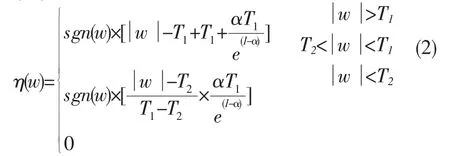
式中，T1、T2分别为上、下阈值，β为关联参数。α可以用于调整阈值函数整体降噪程度，在(0,1)之间取值。该函数克服了函数不连续和恒定偏差的不足，并可以通过改变调节参数来调整降噪幅度和降噪区间。但它不能根据实际信号的噪声能量分布，自适应地调整整体和局部的降噪幅度。

三、改进的小波包双阈值函数

（一）新阈值变换函数

（1）阈值函数表达式

根据上节讨论，对小波包系数w来说，阈值函数均为奇函数。设Cmin、Cmax分别表示小波包系数w绝对值的最小和最大值。参考文献[5]中阈值降噪函数条件：

1.在函数定义域范围内具有单调性且无间断点。

2.在定义域范围内，导函数值逐渐增大，或者先增大再减小，这样才能使小波包系数中间区域的系数差异增大，便于识别。

3.导数（尤其是区间[Cmin,Cmax]中段的导数）应大于1。

根据文献[5]中阈值函数条件和文献[4]中阈值降噪方法的不足，本文在此基础上，定义了下式所示的双参数双阈值函数：

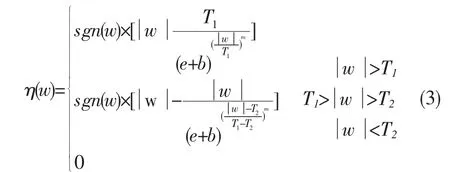
式中，下阈值T2=βT1＜T1；β(0＜β＜1)为阈值关联参数。m、b为本文引入的新的调节参数。下面来证明，新阈值函数不仅满足以上条件，而且具有独特性质。

（2）改进的阈值函数分析

函数的性态包括连续性、单调性、渐进性及凹向等。

1)函数连续性

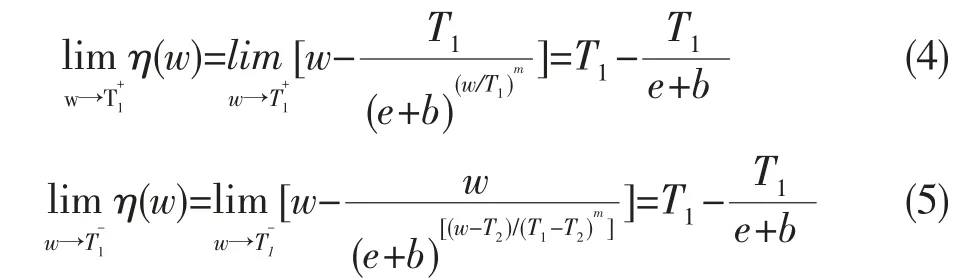
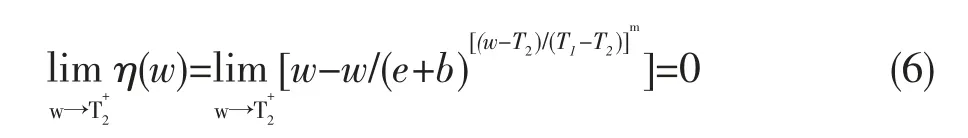
由式(4)～(6)可知，阈值函数η(w)在阈值T1、T2处连续。

2)函数单调性

当T1＞w＞T2时，设w1＜w2

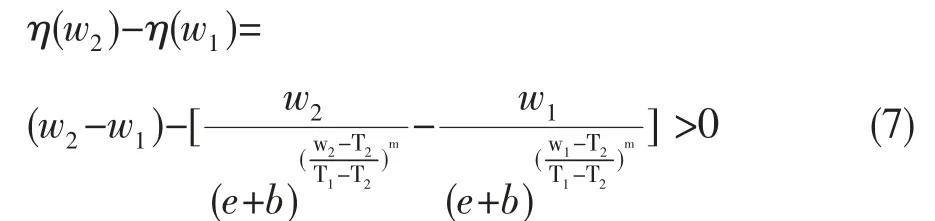
同理，当w＞T1时

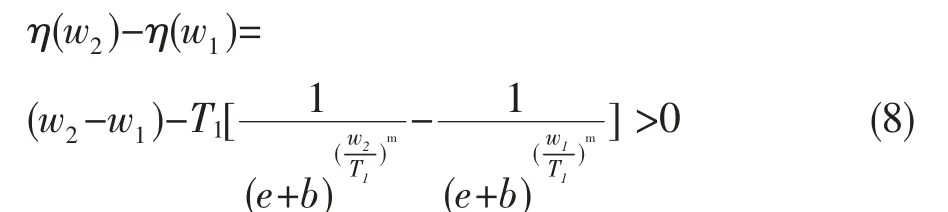
式(3)是奇函数。由上述函数单调性证明得，本文阈值函数在定义域范围内单调递增。故本文阈值函数符合条件(1)、(2)。

3)渐近性

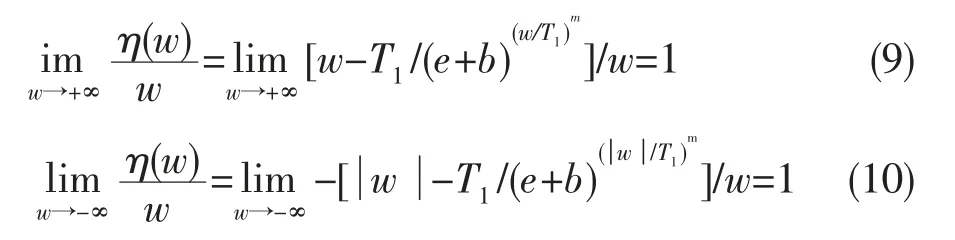
由上述函数推导得，本文阈值函数以y=x为渐近线。与阈值变换函数的条件(3)相符。

4）导函数性态

由于本文阈值函数是奇函数，故下面在[0,+∞)内验证本文阈值函数导函数特性。

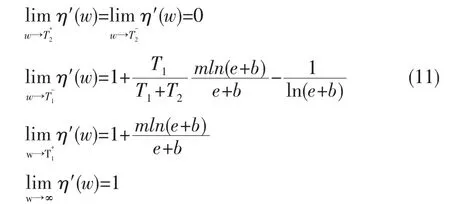
由式(11)得，当m较大时，式(3)的导函数在T1处的导数值大于1。除此之外，式(3)在各阈值区间内均是初等函数组成，因此本文阈值函数在个阈值区间内导函数连续，并以为渐近线。因此，改进后的阈值函数在[T1，+∞)内导函数均大于1。故本文阈值函数符合上述条件(3)。

5)函数偏差性

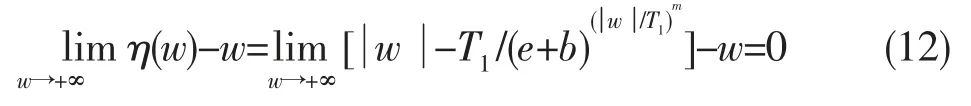
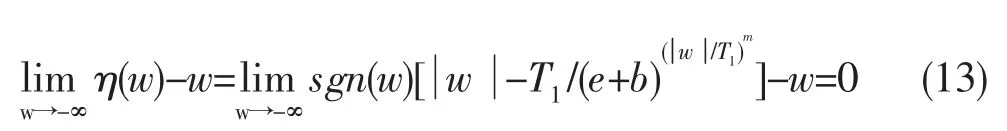
由阈值函数的恒定偏差性证明得，当本文w值趋向于无穷时，η(w)=w。故本文提出的改进后的阈值函数无恒定偏差。

由上述分析可知，改进后的阈值函数在基本满足阈值去噪变换的条件下，继承了文献[4]函数在阈值点连续及无恒定偏差的优点。

6)调节参数m与b影响分析

此部分参数影响分析，令下阈值T2=5，上阈值T1=12。通过控制变量法，调节m与b的值来研究相应阈值函数降噪幅度的影响。结果如图1所示。

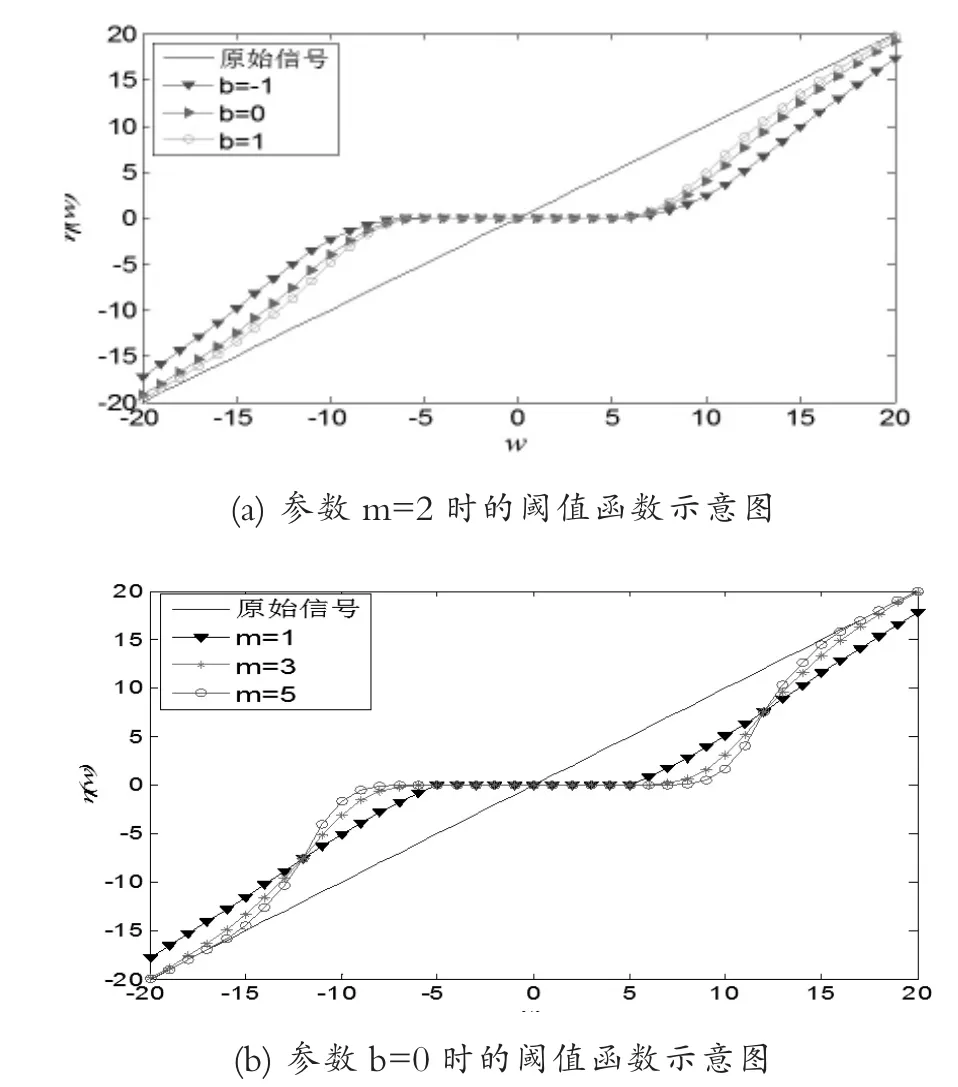
图1 改进阈值函数示意图

由图1（a）可见，m值不变的情况下，b越大降噪幅度越小；反之，降噪幅度越大。由图1（b）可见，b值不变的情况下，m越大函数在不同阈值范围内变化越明显，从而对大于和小于阈值的部分极大程度地保留和收缩，实现有用信息和噪声信息的分离。反之，降噪幅度越小。

（二）阈值及调节参数的确定

(1)参数m的确定

参数m主要反映不同小波包的能量分布。为了进一步提高方法的自适应性，对函数表达式中参数m进行数学建模为：

式中，mj,k表示小波包分解第j层中第k段小波包系数的调节系数。Ej,k是小波包系数的能量，表达式为。Ej是小波包总能量，表达式为Ej=

实际工况下，噪声能量一般大于有用信号，因此，Ejk/Ej值一般较小。另外，由式(3)和图(1)可知，1＜m＜5。综合考虑，m0=1，α=10。

(2)上下阈值的确定

文献[4]中指出利用sqtwolog准则选取的阈值一般偏大的特点。除此以外，现有阈值选取准则，均存在自身的不足。针对现有方法的特点，文献[6]指出：采用sqtwolog准则选取上阈值T1，再通过T2=βT1(0＜β＜1)确定下阈值能尽可能地保留有用信号。但阈值关联参数?应和调节因子b一起遍历选取，以达到最好的降噪效果。

(3)参数b的取值范围

由式(3)可知，为了对小波包系数实现收缩作用，分母(e+b)应大于1。但数值试验表明：若(e+b)过大，反而降噪效果较差。因此，本文选定参数b在[-1.5，1.5]之间取值。对于不同信噪比的信号，若参数b的取值跨度较大，易造成降噪不充分或过度降噪的情况，相反跨度较小，虽避免了上述情况，但会极大地增加计算量。

(4)参数b和系数k的联合确定

本文首先通过sqtwolog准则确定上阈值T1的值。其次根据式(14)确定实际信号经小波包分解后每频段能量分布系数m。最后，以降噪后信号的最大信噪比为目标函数，在b和k的调节范围内，选择最佳的b和k的参数组合。具体方法如下：

(1)在b和k的取值范围内，选择合适的步长△b和△k，并以此分别将对应区间等分成M和N份。

(2)由步骤(1)得到一个参数矩阵D，其包含M×N个数据点。每个数据点代表一种b和k的组合。遍历该矩阵中的每个数据点，利用式(3)进行降噪，以最大信噪比作为目标函数[7]确定最佳参数组合。

四、仿真与试验验证

文献[4]中的阈值函数通过引入双调节因子，使其能够灵活地调整函数降噪幅度。但其忽略了小波分解后能量分布的影响，针对这一点，本文在其基础上进行改进。基于此，本节欲通过仿真和试验信号验证改进后阈值函数的有效性。

（一）仿真信号验证

首先通过Matlab软件仿真冲击信号(bumps)，并由wnoise函数对仿真信号添加不同程度高斯白噪声，以仿真不同信噪比的原始信号。然后采用传统双阈值法、文献[4]中的阈值方法和本文提出的阈值方法对不同信噪比的仿真信号进行降噪处理。最后计算不同方法降噪重构后对应信号的信噪比(SNR)和均方误差(RMS)。

以SNR=3的冲击信号为例，不同方法降噪重构后的信号分别如图2所示。

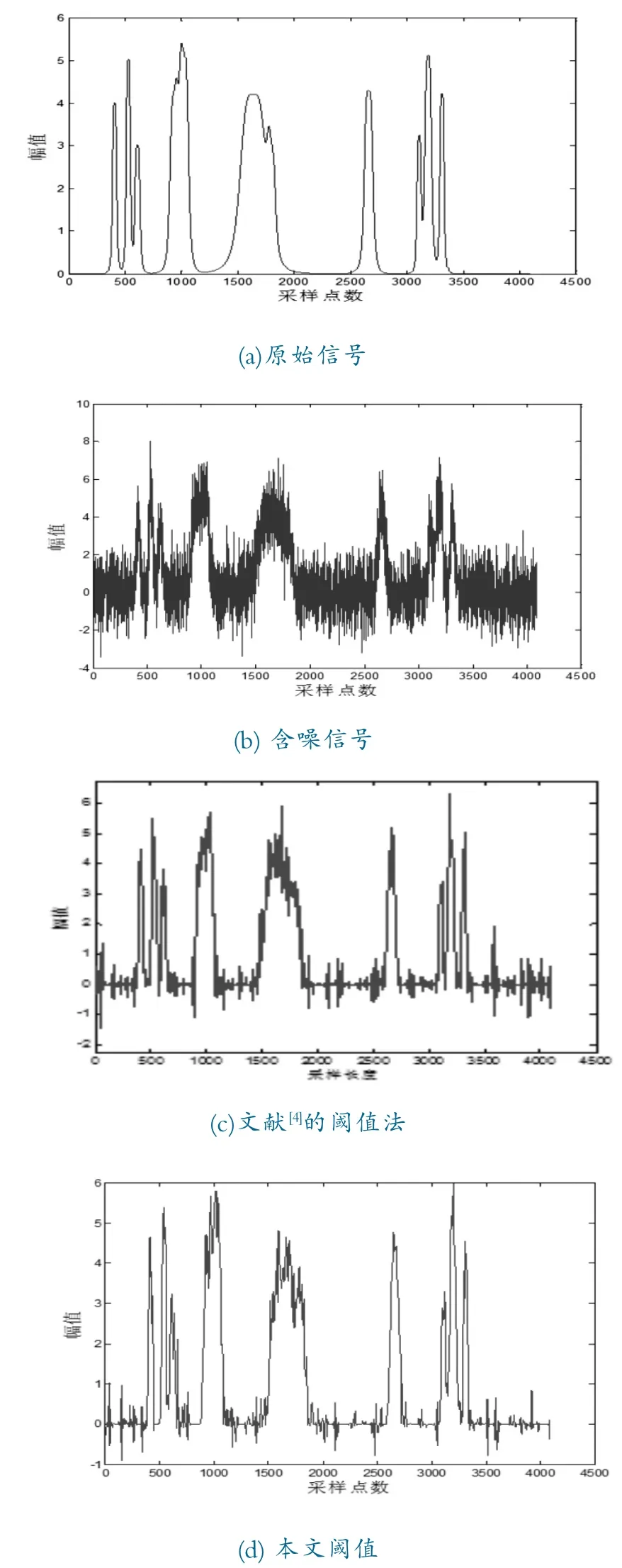
图2 仿真信号降噪效果图

由图2(a)和图2(b)可见，在SNR=3的信噪比下，原始冲击信号(bumps)的冲击特征已基本被淹没。由图2(c)可见，文献[4]中的双阈值法能有效地降低噪声对冲击特征的影响，但仍出现大面积的信号震荡现象，且信号突变部分的处理较为粗糙。由图2(d)可见，改进后的阈值函数的降噪效果要明显优于文献[4]的方法。另外，比文献[4]的方法更有效地抑制了信号震荡现象，震荡幅度更小且突变部分处理较好。

为进一步研究不同信噪比下本文阈值函数的降噪效果，采用不同信噪比的仿真信号，对比计算不同方法降噪后的信噪比和均方误差，计算结果如下表1、2所示。

表1 不同阈值函数去噪后信噪比

由表1和表2可见，无论是去噪后信号的信噪比还是均方误差，通过本文提出的新阈值函数处理后的信号均优于传统降噪方法。与图2的分析结果相同。

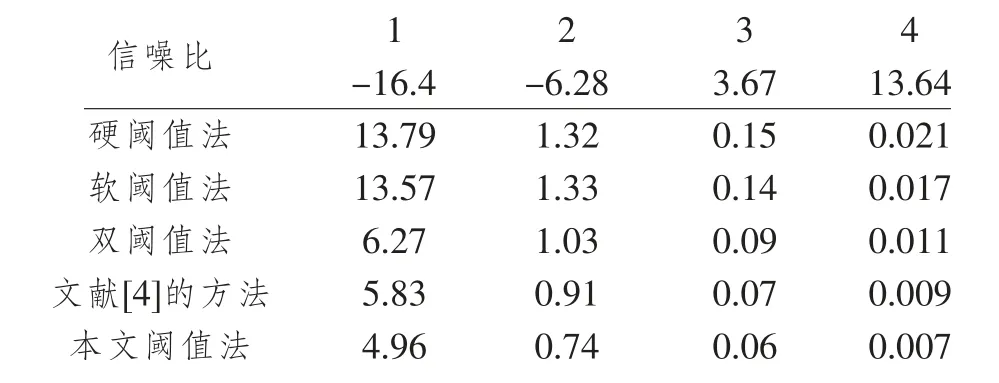
表2 不同阈值函数去噪后均方误差

（二）试验信号验证

本节统一选取行星齿轮箱太阳轮裂纹故障实验信号为分析对象。实验内容、步骤、故障设置及信号采集过程等如文献[8]所述。利用不同降噪方法对加噪信号进行降噪处理，并计算每种方法降噪重构后信号的信噪比，结果如表3所示。

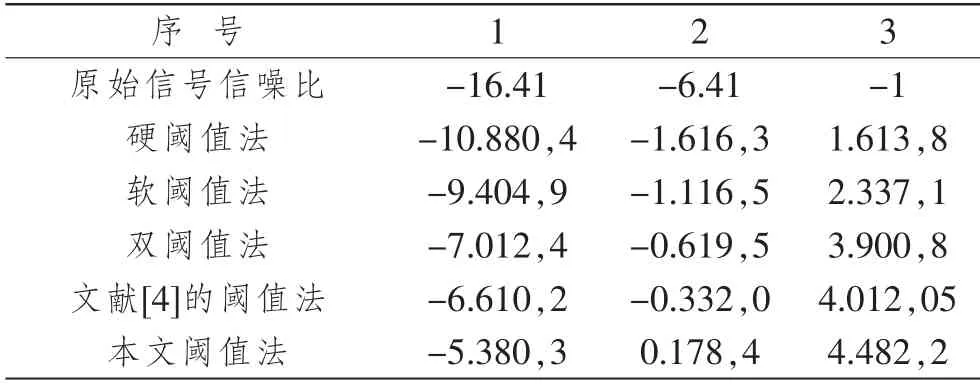
表3 不同降噪方法去噪后信噪比

由表3可见，在不同信噪比情况下，相比于其他降噪方法，改进后的阈值法降噪后信号的信噪比更高，即降噪效果更明显。进一步验证了本文提出的阈值方法的有效性。

五、结论

现有的阈值函数已函数连续且无恒定偏差，且通过改变调节因子大小改变函数降噪程度，但其不能根据实际信号中噪声能量的分布自适应地调整不同频段的降噪幅度，故而降噪效果不够理想。针对这一问题，本文引入了两个新的调节参数，提出了一种双参数的双阈值函数。改进后的阈值函数在基本满足阈值变换的条件下，亦函数连续且无恒定偏差。另外，函数通过调节新的调节参数b和m值，使改进后的函数能够根据实际信号中的不同频段内噪声及有用信号的能量分布，自适应的调整函数整体和局部的降噪幅度。最后利用仿真和试验信号，对比验证了改进后阈值方法的有效性。