连接器信号串扰优化浅析
2022-05-06刘兴平岳明旗
刘兴平,左 静,陈 惠,王 超,岳明旗
(四川华丰科技股份有限公司,四川绵阳,621000)
1 引言
近年来,随着技术发展,消费者对产品的倾向越来越小,速率越来越高,在这种情况下,就必须更加注意电路中串扰现象。对产品信号完整性的要求越来越高,解决信号完整性问题关系到信号速率是否能够再次提升,以满足市场的需求。
通常SI工程师在产品研发阶段,经常会遇到各种各样的信号完整性问题,就拿高速连接器来说,因为连接器结构复杂,所以串扰优化也是最困难的,本文通过解析串扰原理及借用实际工作中经验提出了优化串扰的常用手段。
2 串扰产生的原因
串扰指的是当信号传输过程中,电磁能量耦合到其他了其他的传输线上,而这个耦合能量是不期望的能量。串扰在数字链路中普遍存在,包括芯片、PCB、连接器、电缆等。串扰将会通过改变线路的传输特性来影响信号完整性以及时序特征,也会将噪声耦合入传输线,这将损害信号完整性减少噪声裕量。
2.1 互感和互容
从电路角度看,串扰是由于临近两导体之间的互感和互容引起,这两种现象都是在线路间通过磁场(互感作用)和电场(互容作用)耦合能量产生的[1]。
感性耦合是由于干扰源上的电流变化产生的磁场在被干扰对象上引起感应电压从而导致的电磁干扰,如图1.

图1 互感耦合原理
互感是引起串扰的两个重要因素之一,互感系数LM标志了一根驱动传输线通过磁场对另外一根传输线产生感应电流的程度。从本质上来说,如果“受害线”和“侵略线”的距离足够接近,以至于侵略线产生的磁场将受害线包围其中,如图2,则在受侵略的传输线上将会产生感应电流,而这个通过磁场耦合产生的电流在电路模型中就通过互感参数来表征。

图2 传输线磁场及电场耦合
互感 LM的作用下,将根据侵略线上的电流变化率而在受害线上引起一定的噪声,噪声电压的大小与电流变换率成正比,通常可由下列公式(1)来计算[2]:
△υL=Lm di/dt
(1)
由于感应噪声正比于信号的变化率,互感在高速数字电路的应用中显得尤为重要。
容性耦合是干扰源上的电压变化在被干扰对象上引起感应电流从而导致的电磁干扰,如图3.

图3 互容耦合原理
互容是引起串扰的另外一个重要因素,互容是两导体间简单的电场耦合,这种耦合在电路模型中以互容的形式表现出来。互容Cm将产生一个与侵略线上电压变换率成正比的噪声电流到受害线,通常可以由下列公式(2)来计算:
△iC= Cmdv/dt
(2)
同样,感应噪声也是正比于信号的变化率,说明互容也是非常重要的。
2.2 近端串扰与远端串扰
容性耦合和感性耦合总是同时发生的,受害线上同时包含了容性耦合电流与感性耦合电流。在两根信号线耦合较弱时,总串扰近似为容性串扰与感性串扰的累加。受害线上与攻击信号传播方向相反的一端称为近端,与攻击信号传播方向相同的一端称为远端。由于两种耦合,在受害线的近端产生的串扰称为近端串扰,记为VNEXT,在受害线的远端产生的串扰称为远端串扰,记为VFEXT。图4直观地显示了两种耦合电流的产生、流动方向、近端串扰和远端串扰以及它们之间的关系。

图4 近端串扰与远端串扰
从串扰的产生可以得知,串扰主要是因为互感和互容耦合引起,互感和互容为串扰提供了攻击路径,所以优化串扰应该从耦合上做文章。
3 降低串扰的常用手法
3.1 增大平行走线间距
对于串扰来讲,增大平行线走线间距是改善串扰最直接也是最有效的方式,由于串扰的来源主要是容性耦合和感性耦合,如图2,拉大走线间距能有效减少走线间的互容和互感,从而减小串扰。
如图5所示,建立一个带状线模型,保持其他变量不变,分别设置间距S1值为10mil、20mil、30mil,对比不同间距串扰值。
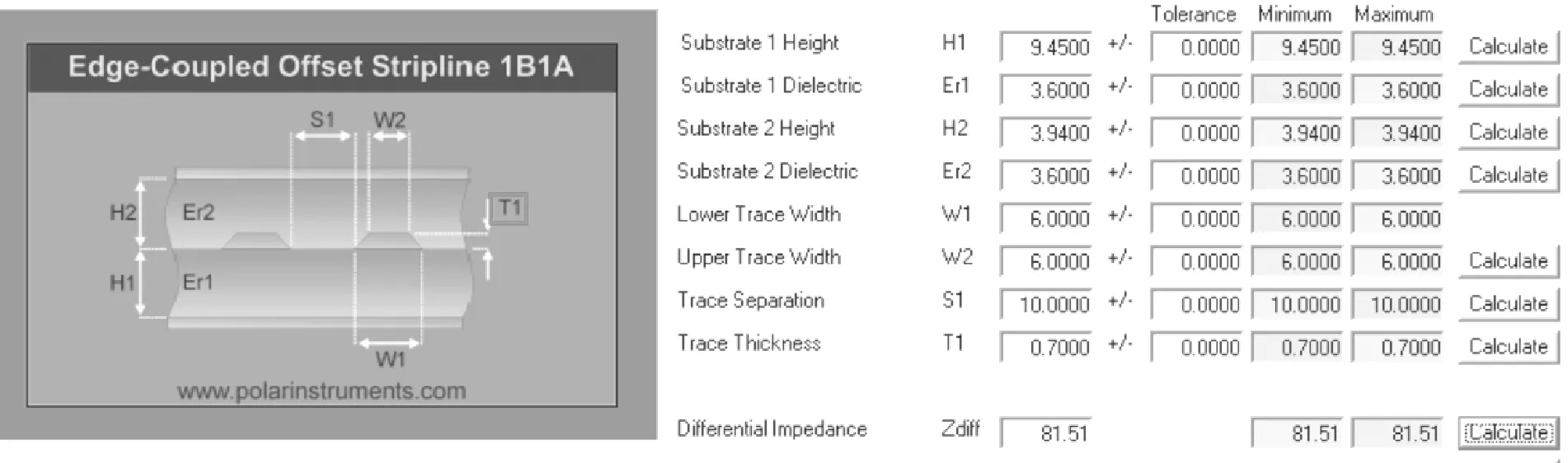
图5 带状线串扰模型
串扰仿真结果如图6所示。
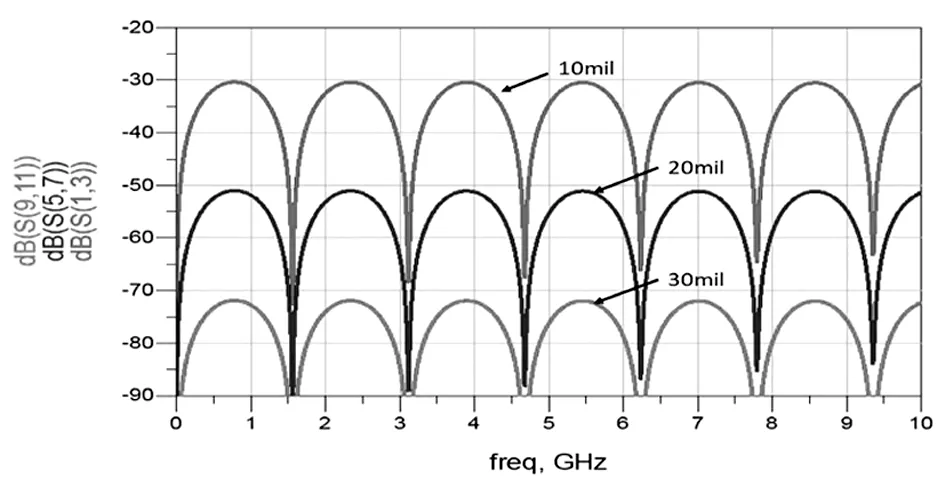
图6 不同间距串扰仿真结果
由图6可知,随着间距S1不断增大,串扰将不断减小,这也符合串扰的产生原理,所以增大走线间距是减小串扰的最有效方式。
3.2 增加保护地线
串扰的路径是容性耦合和感性耦合,我们需要明白的是只要是金属与金属之间就会产生耦合电感和耦合电容,距离近的耦合大,距离远的耦合小。同样,增加保护地线,实际上就是提供了信号与保护地的耦合路径,串扰遵循哪儿电容大去儿,哪儿电感小去哪儿的规律,所以理论上增加保护地线,将会减小串扰耦合。
a.我们按差分信号间距4mm建立模型,当间距不变情况下,在差分信号中间增加会留地GND,仿真对比串扰差异,如图7所示。

图7 两种不同的串扰模型
串扰仿真结果:

图8 是否带保护地仿真结果对比
按图8仿真结果,增加保护地能够减小串扰,这就是我们经常看到高速信号都带有保护地的原因,因为空间原因,当信号间间距不能再增大时,增加保护地是一个改善串扰的有效方式。
通过上述理论,我们知道增加回流地会减小串扰,我们厂家的PCB板会使用完整的参考平面,这将继续增大信号与地的耦合,依据理论,耦合能量会向电容大和电感小的地方前进,则使用完整参考平面将会进一步减小串扰。
b.在CASE1和case2的基础上,我们增加一个距离信号0.25mm的参考平面,如图9,对比串扰值。

图9 加屏蔽的串扰模型
串扰仿真结果如图10所示。

图10 加屏蔽仿真结果对比
从图10仿真结果可以看出,当增加屏蔽后,CASE3和CASE4的串扰都比不增加屏蔽效果好,且两种方式串扰值基本重合,所以增加屏蔽接地能有效的降低串扰。
CASE3和CASE4的仿真结果虽然重合,但并不代表所有的情形,因为文中仿真只到10GHz,所以不代表更高频段结果,按照设计经验更高频段将会体现出差异值。要想保证CASE4中的串扰更好,需要保护地搭接点数量够多且密度大,一般需要遵循搭接点距离小于λ/4。对于搭接点过少,且信号速率变得更高的时候,增加保护地线将会起到相反的效果,会导致串扰变差且出现谐振,还比不上CASE3,其结果将会类似后面的CASE5情形,所以使用CASE4需要重点关注。事实上,当在更高速率的产品设计时,CASE4将会给高频段串扰带来更好的结果,前提是设计时能提供更多更密的搭接点。
我们注意到,带保护地线与屏蔽有两个点首尾搭接,如果不搭接是否会影响串扰呢?我们按一下建模再分析。
c.在CASE2基础上,建立CASE5保护地线首尾不增加搭接点,CASE6整个保护地线全部搭接,如图11,建立模型仿真。

图11 保护地与屏蔽搭接点串扰模型
串扰仿真结果如图12所示。

图12 保护地与屏蔽搭接点仿真结果对比
从如图12中可以看出,当保护地和屏蔽无搭接时,串扰将会恶化,而仿真中的保护地首尾相连CASE2、无保护地CASE3以及保护地与屏蔽全搭接CASE6的仿真可以看出,串扰基本一致,这是因为信号耦合到保护地上时,当保护地搭接点数量足够时,会给耦合回流提供最短路径,保护地上的信号回流会以最短时间最短路径回到屏蔽上,所以表征出的串扰结果相差不大,当然,保护地与屏蔽的搭接点应遵循规律,搭接点与点的距离最好小于λ/4,λ为入射波的波长。
我们在进行高速连接器走线设计时,应尽量避免出现CASE5情况,当保护地与屏蔽未搭接时,信号的回流路径将被一分为二,而耦合到保护地上的回流将需要绕到更远的地方才能回到屏蔽上,这就直接导致了串扰变差,严重的将会产生谐振,影响信号完整性。
由以上案例可知,信号速率越高,回流地的设计将会起到至关重要的作用,特别上现在连接器越来越高密度且小型化。
3.3 最小化平行走线长度
我们见得最多的走线是平行走线,因为能节约空间进行更多信号的布局。按照电磁场理论,串扰是因为互感和互容,如果两条信号线互相垂直,磁感线耦合到另一信号线上的机会将会非常的小,如图13,串扰也会很小。如果条件允许空间阻抗,是否可以带角度布线或者垂直布线呢,其实同平面采用这种方式基本不可行,特别是连接器,垂直走线将会使空间利用率极低,还不如将信号线间距拉大。由于PCB走线不同层可实现垂直布线,可以使用该方法降低层间串扰。

图13 耦合线
3.4 阻抗匹配
对于高速数字信号传输,如果阻抗不匹配,就会发生反射。同理,当信号沿传输线传播时,遇到阻抗不匹配,则会发生反射,而反射的信号同样会耦合到受害线端,造成串扰增加,传输线上的阻抗不匹配处往往会发生多次反射,周而复始,直至幅度衰减为0,如下图14为反射过程。
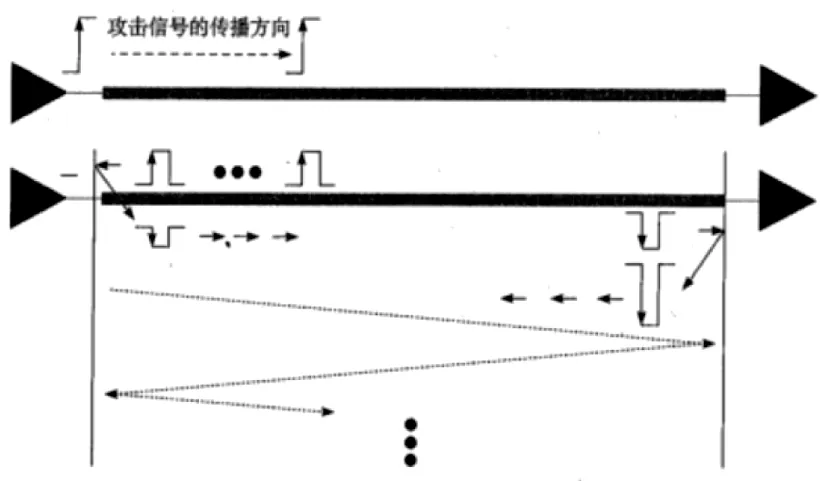
图14 串扰反射
建立一组仿真模型,一组传输线阻抗匹配P1,一组增加两个不匹配点P2,如下图15,观察其串扰结果。

图15 阻抗模型
其串扰仿真结果如图16所示。
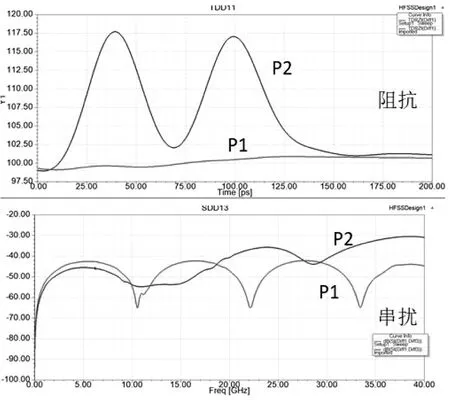
图16 阻抗及串扰对比
由图16可知,阻抗不匹配的P2模型随着频率增加,串扰呈明显的上升趋势,而阻抗匹配的串扰增长比较缓慢,所以阻抗匹配有助于改善串扰。
I.保持回流地平面完整
高速连接器及PCB设计中经常会用到完整的屏蔽片作回流地,连接器由于冲制加工等因素,屏蔽片的形状经常会有掏空部分,PCB因为过孔反焊盘及阻抗匹配,也会存在掏空部分。这些空洞会使电磁场的耦合泄露到相邻的信号线,从而产生串扰,特别是对于高速背板的相邻层,对串扰的影响尤其明显。
建立一个相邻层的模型,如图17,模型a为相邻层不掏空,模型b为相邻层屏蔽增加两个空洞,仿真对比串扰大小。

图17 相邻层屏蔽模型
串扰仿真结果:

图18 屏蔽对比仿真结果
由仿真结果可知屏蔽完整的a模型串扰非常好,曲线光滑,而b模型走线两侧增加空洞后串扰明显变差,且在25G左右出现谐振。可见屏蔽完整性会影响串扰。
II.使用介电常数更低的绝缘材料
就介电常数 E ,本身来说,对串扰的影响微乎其微。对于图19所示的横截面积尺寸,当介电常数为4.2时,阻抗约为50Ω。如果不考虑阻抗控制,保持横截面几何结构不变,仅仅换成介电常数为3.4的板材,容性相对耦合度与感性相对耦合度变化趋势如图20所示,横轴表示介电常数,纵轴表示相对耦合度。图21为结构完全一致,只是改变了介电常数的串扰仿真值,可以看出串扰基本没什么变化,介电常数的变化对于相对耦合度几乎没有影响。因此,介电常数 E ,本身并不影响串扰的大小[2]。

图19 层叠结构

图20 相对耦合度与介电常数
当使用小介电常数的板材时,为了阻抗控制,必须使用更薄的介质,介电常数为3.4时,为了阻抗保持为50欧姆,需要修改横截面尺寸,如图21所示,介质变薄。此时相对耦合度如图22所示。介电常数为3.4时,相对耦合度明显减小;使用介电常数较小的板材,其串扰明显减小。
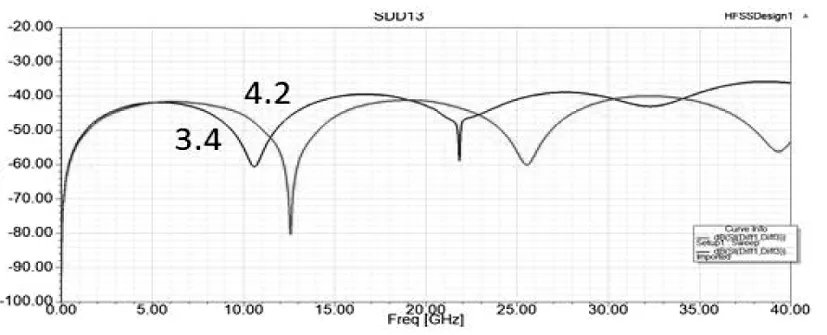
图21 结构相同介电常数不同的串扰值

图22 介质变薄层叠结构

图23 阻抗控制的相对耦合度
介电常数本身不影响串扰,但是因为阻抗匹配,使用低介电常数因为阻抗匹配会拉近信号与地的耦合,因此间接的降低了串扰。
4 结束语
对于高速类产品,串扰的优化是极其重要的部分,本文通过电磁场理论衍生到实际仿真应用,着重描述了串扰的产生及优化方式,为高速连接器及PCB设计串扰优化提供一些改进方向。
