随钻方位电磁波测井响应快速正演方法与地质导向应用
2022-05-05岳喜洲刘天淋李国玉聂在平马明学孙向阳
岳喜洲, 刘天淋, 李国玉, 聂在平, 马明学, 孙向阳
1 电子科技大学电子科学与工程学院, 成都 611731 2 中国海油田服务股份有限公司油田技术研究院, 北京 101149
0 引言
随钻方位电磁波测井技术是大斜度井/水平井实时地质导向的关键,在海上和非常规油气藏勘探开发中发挥着重要作用(Wu et al., 2020a,b; Pardo et al., 2015; Fang et al., 2008; 王磊等, 2018).相比于传统无方位的随钻电阻率仪器,随钻方位电磁波测井可实现对地层界面、电阻率等信息实时反演,从而将被动式导向升级为主动式导向,极大地提高了储层钻遇率(Wang et al., 2019; Wilson et al., 2019;王磊等, 2020; 胡旭飞等, 2018).如何实现随钻方位电磁波测井快速、精确正演,是其实时反演的关键.各向异性介质电磁场正演方法可分为三类:一维解析法、二维半解析半数值法、三维数值法.其中,三维数值法可适用于复杂地层条件,可对仪器结构进行精细模拟(Teixeira, 2008),但其计算量大,复杂度高,不适用于实时地质导向;二维半解析半数值法计算速度快,可应用于直井地层侵入等模型下的仪器响应研究(Wang et al., 2009),不适用于大斜度井/水平井实时地质导向;一维解析法针对径向或纵向分层地质模型,对仪器响应解析求解,具有速度快、精度高等优点(肖加奇等, 2013),是当前随钻电磁波测井实时反演的基础.国际各大油服公司的随钻方位电磁波测井仪均搭载了相应的一维正演算法,如斯伦贝谢PeriScope(Li et al., 2005)、阿特拉斯Azitrak(Wang et al., 2007)、哈里伯顿ADR(Bittar et al., 2007)等.
近年来,各向异性介质电磁场解析计算得到快速发展,介质模型由单轴各向异性发展到双轴各向异性,甚至全张量各向异性(Løseth and Ursin, 2007; Yuan et al., 2010; He et al., 2016).在数理意义上,双轴各向异性、全张量各向异性介质模型更具有普适性(邓少贵等, 2020;Hu et al., 2018),单轴各向异性介质模型可由其退化而得.但对于随钻电磁波测井尺度而言,特别是海上随钻测井,绝大部分地层表现为各向同性,或单轴各向异性.双轴各向异性、全张量各向异性介质模型电磁场计算通常需要双重积分,计算复杂度较高,难以适用于实时反演;而单轴各向异性介质模型电磁场通常为含贝塞尔函数的一重积分,高斯积分、快速汉克尔变换等积分方法均可实现其快速计算(莫平华, 2007; Guptasarma and Singh, 1997; Kong, 2007).因此,目前在随钻电磁波测井领域,单轴各向异性地层模型及其快速算法更具代表性与适用性.
针对平面分层各向异性介质麦克斯韦方程组一维求解方法,可分为镜像源法(Wang and Liu, 2014)、并矢Green函数法(魏宝君等, 2007)、TE波与TM波分离法以及Hertz势函数法(Zhong et al., 2008;陈赟等,2021)等.当利用边界条件进一步确定各层中的场系数时,又可分为广义反射法和系数递推法(姚东华等, 2010)等.虽然物理意义上场的传播是收敛的,但在解的推导过程中,中间变量常出现指数增大项,受计算机位数限制,易出现数值上溢或下溢情况.为解决数值计算中的场溢出问题,Zhong等(2008)对系数递推过程中的传递矩阵进行变形,压制了因层厚等原因造成的数值溢出,取得了一定成效.Hong等(2014)引入振幅消除了TE波、TM波在传播过程中的指数增大项,使得算法适用于任意多层介质模型,压制了积分上限等原因造成的数值溢出.在早期工程计算中,为避免因层厚导致数值溢出,有学者将厚层分解为多个电阻率一致的薄层,但该方法将引入“假界面”,从而降低计算效率.因此,基于层状各向异性介质电磁场全张量一维正演方法,消除工程计算中的数值溢出,可实现随钻方位电磁波测井响应收敛、快速正演模拟.
本文基于赫兹势函数法求解各向异性介质中的麦克斯韦方程组,不同于Zhong等(2008),对解中的指数增大项进行了改造,并消除系数递推矩阵中的溢出因子,使得递推过程完全收敛.然后,将所得的无溢出各向异性介质全张量电磁场快速正演算法应用到随钻方位电磁波测井领域,对国产随钻方位电磁波测电阻率井仪DWPR信号响应进行分析,原始信号正演分析表明,与国外同类仪器相比,DWPR特有的双斜线圈系进一步提升了探边距离,达到了国际领先水平.最后以物理实验与地质导向实例验证算法的可靠性与高效性,以及仪器的稳定性与实用性.
1 一维各向异性介质正演解析算法
1.1 层状各向异性介质中麦克斯韦方程组的解
各向异性层状介质中若只存在时谐磁偶极子源时(图1),麦克斯韦方程组可写为(时谐因子取e-iω t):
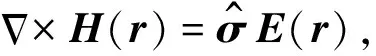
(1)
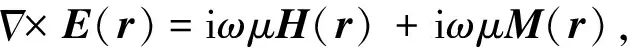
(2)
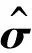
(3)
式中,σh指介质水平方向电导率,σv指介质垂直方向电导率.
引入赫兹势函数Π,与电磁场E、H关系为:
(4)
(5)
以及洛伦兹规范条件:
(6)
代入式(1)、(2),得到Π的波动方程后对其进行求解,即可得无限厚介质中势函数Π通解,层状各向异性介质中势函数Π表达式可写为通解与特解之和.
当磁偶极子源沿z方向发射时,Πx、Πy均为0,Πz可写为:
×kρJ0(kρρ)dkρ,
(7)
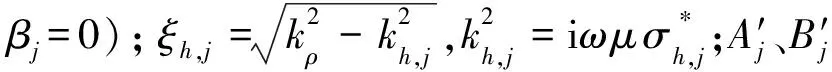
×kρJ0(kρρ)dkρ,
(8)
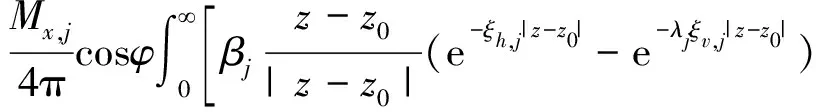
-ξv,jP′je-λjξv,jz+ξv,jQ′jeλjξv,jz
+S′je-ξh,jz+T′jeξh,jz]J1(kρρ)dkρ,
(9)

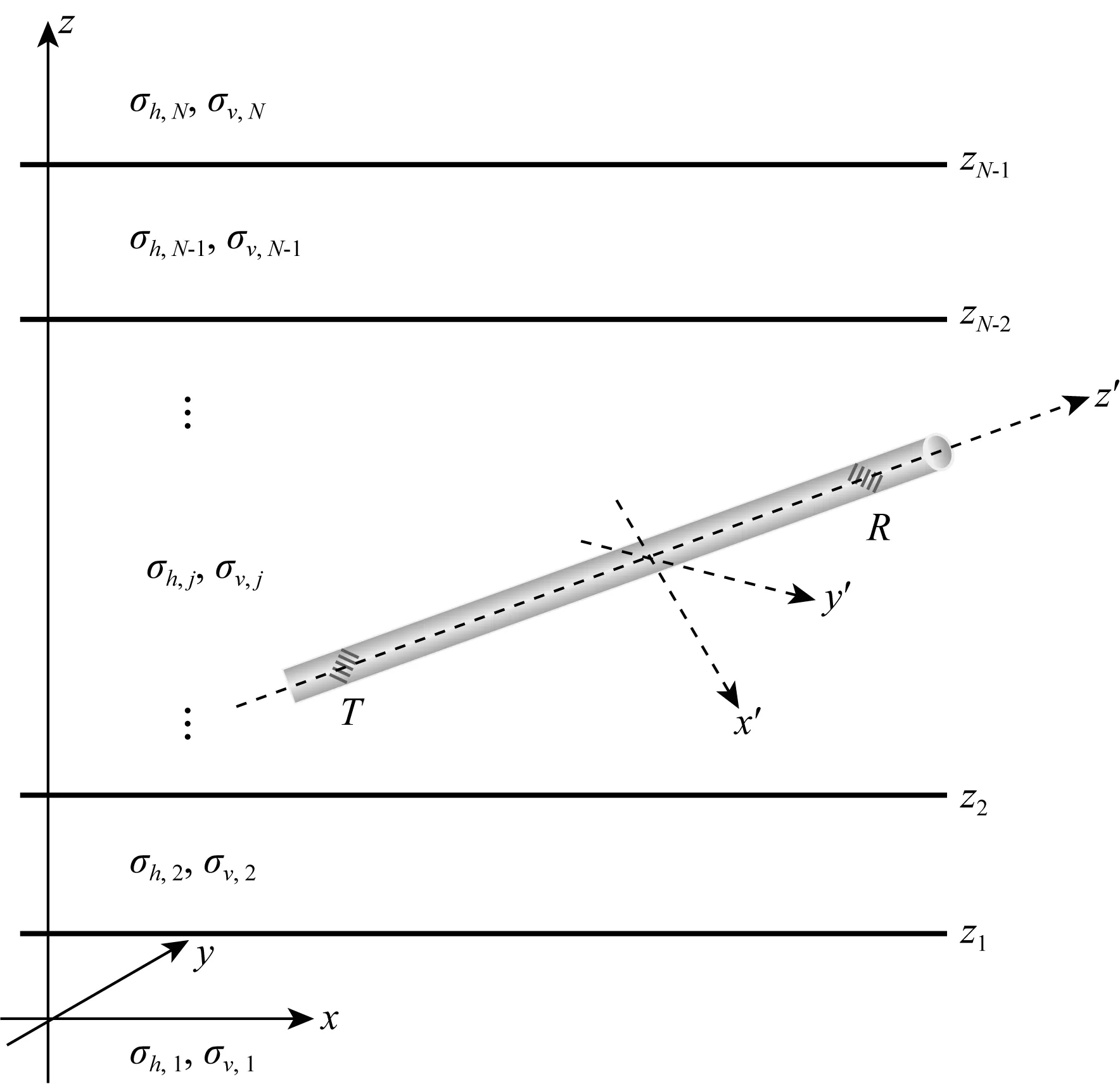
图1 层状各向异性介质模型Fig.1 Layered anisotropic formation model
1.2 系数收敛递推法
式(6)、(7)、(8)中,由于z可为任意实数,积分变量kρ∈(0,∞),故z>0时eξh,jz、eλjξv,jz项为指数增大项,z<0时e-ξh,jz、e-λjξv,jz项为指数增大项,在计算过程中将会存在严重的数值溢出问题.因此,考虑到场的收敛性与衰减性,在上述表达式中引入地层边界位置.磁偶极子源沿z向发射时,将式(7)改写为:
×kρJ0(kρρ)dkρ,
(10)
磁偶极子源沿x向发射时,式(8)、(9)改写为:
+Qjeλjξv,j(z-zj))kρJ0(kρρ)dkρ,
(11)
-ξv,jPje-λjξv,j(z-zj-1)+ξv,jQjeλjξv,j(z-zj)
+Sje-ξh,j(z-zj-1)+Tjeξh,j(z-zj)]J1(kρρ)dkρ,
(12)
式中,zj-1、zj分别表示第j-1、j个界面.Aj、Pj、Sj可认为是Hertz势在第j-1个界面处向上传播的波幅,e-ξh,j(z-zj-1)、e-λjξv,j(z-zj-1)则代表其传播的衰减模式;Bj、Qj、Tj可认为是Hertz势在第j个界面处向下传播的波幅,eξh,j(z-zj)、eλjξv,j(z-zj)则代表其传播的衰减模式.
由于第1层为向下延伸的半无限厚层,不存在下界面,故A1、P1、S1均为0;类似的,第N层为向上延伸的半无限厚层,不存在上界面,故BN、QN、TN均为0.相应的电磁场表达式可以此类推.
在第j个界面处,电磁场切向分量连续:Hx,j=Hx,j+1,Hy,j=Hy,j+1,Ex,j=Ex,j+1,Ex,j=Ex,j+1.首先考虑无源区,对于沿z向发射的磁偶极子源:
(13)
可得:

ξh,iAie-ξh,i(zi-zi-1)-ξh,iBieξh,i(zi-zi)=ξh,i+1Ai+1e-ξh,i+1(zi-zi)-ξh,i+1Bi+1eξh,i+1(zi-zi+1),
(14)
μi(Aie-ξh,i(zi-zi-1)+Bieξh,i(zi-zi))=μi+1(Ai+1e-ξh,i+1(zi-zi)+Bi+1eξh,i+1(zi-zi+1)),
(15)
以hj表示第j层层厚,即hj=zj-zj-1.令:
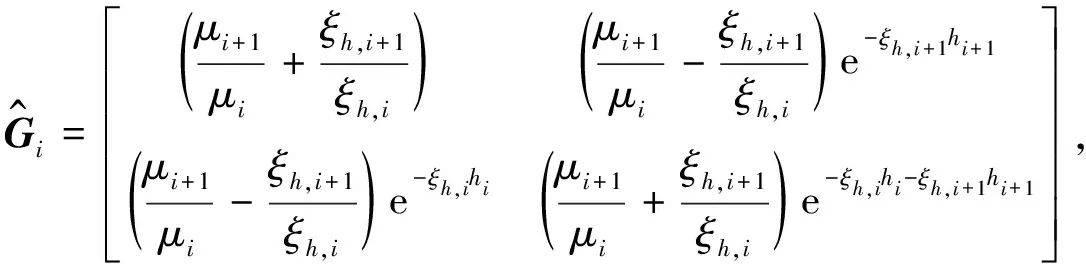
(16)
(17)
可得系数递推式:
(18)
同样的,对于沿x向发射的磁偶极子源:
μi(-ξv,iPie-λiξv,ihi+ξv,iQi)=μi+1(-ξv,i+1Pi+1+ξv,i+1Qi+1e-λi+1ξv,i+1hi+1),
(19)
(20)
μiSie-ξh,ihi+μiTi=μi+1Si+1+μi+1Ti+1e-ξh,i+1hi+1,
(21)
ξh,iSie-ξh,ihi-ξh,iTi=ξh,i+1Si+1-ξh,i+1Ti+1e-ξh,i+1hi+1,
(22)
令:
(23)
(24)
可得系数递推式:
(25)
(26)
值得注意的是,式(18)、(25)、(26)中的溢出因子eξh,jhj、eλjξv,jhj等项被单独提取,以方便观察、处理.
然后考虑有源区.假设源位于第m层,在界面z=zm处,朝z向、x向发射的磁偶极子源,分别有:
(27)
(28)
(29)
在界面z=zm-1处,有:
(30)
(31)
(32)
结合系数递推式(12)、(13)、(14),可得:

(33)
(34)
(35)

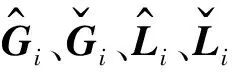
1.3 算法验证
当仪器坐标系与地层坐标系不重合时,已有大量文献证明地层坐标系下的场与仪器坐标系下的场可由旋转矩阵R进行转换,如Zhang等(2004)、邓少贵等(2021),这里不再赘述.
本文采用Guptasarma和Singh(1997)所述120/140点快速Hankel变换计算0阶/1阶贝塞尔函数广义积分,以实现单轴各向异性介质中电磁场快速计算.本文所述算法与格林函数法(魏宝君等, 2007)、截断溢出法在Oklahoma地层模型(图2a)下进行对比,计算结果如图2b、c所示,其中仪器频率为2 MHz,源距为101.6 cm,相对井斜角为60°.由图2可知,截断溢出法在层厚较大和电阻率变化较大的层位出现明显误差,其原因为核函数在该情况下容易溢出,导致积分被截断.而本文所述方法与格林函数法结果一致,从而证明本文所述方法的正确性.
2 随钻方位电磁波测井响应
近年来,随钻方位电磁波测井技术得到广泛应用,极大地提高了大斜度井、水平井储层钻遇率,为油气资源勘探与开发提供了强有力的支撑.国际三大油服公司10余年前便相继推出随钻方位电磁波测井仪,占有国际绝大部分随钻探边市场;国内中海油服于2019年推出了自主研发的商用随钻方位电磁波测井仪DWPR,在渤海油气田等取得良好应用;DWPR仪器结构异于斯伦贝谢、贝克休斯与哈里伯顿的随钻探边仪器,本文结合DWPR仪器结构,从正演角度阐述仪器响应特征及算法应用情况.
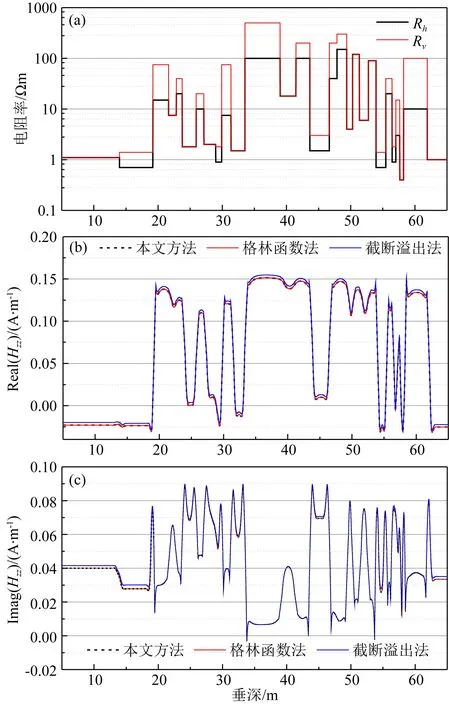
图2 Oklahoma地层模型及Hzz分量响应Fig.2 The Oklahoma formation model and the responses of Hzz
2.1 DWPR原始信号响应
如图3所示,DWPR仪器中包含轴向发射-轴向接收、轴向发射-倾斜接收、倾斜发射-轴向接收、倾斜发射-倾斜接收四种线圈系结构.在井下测量时,仪器旋转一周进行采样,轴向发射-轴向接收线圈系(常规线圈系)接收信号为场zz分量信号,轴向发射-倾斜接收(单斜线圈系)与倾斜发射-轴向接收磁场信号类似,均可用一阶三角函数表示(马明学等, 2018):
(36)

图3 DWPR仪器结构Fig.3 The structure of DWPR tool
式中,φ表示仪器自旋角度.倾斜发射-倾斜接收线圈系(双斜线圈系)磁场信号可用二阶三角函数表示:
(37)
基于上述信号构成,建立7层地层模型,层厚均为5 m,以中频(400 kHz)、长源距线圈系(208.28 cm、243.84 cm)为例,仪器以89°穿过地层,其单斜、双斜线圈系原始磁场信号幅度、相位响应如图4所示.图4中Rh与Rv分别为地层水平、垂直电阻率.
这里假设仪器匀速钻进,图4中A82M、P82M表示208.28 cm(单斜)线圈系旋转一周均匀采样16个扇区的幅度、相位值在深度上的均匀展开,A96M、P96M表示243.84 cm(双斜)线圈系旋转一周均匀采样16个扇区的幅度、相位值在深度上的均匀展开.由图5可知,208.28 cm、243.84 cm原始相位、幅度信号在地层边界处波形幅度明显增大,并且仪器由高阻入低阻、低阻入高阻时,波形幅度各不相同,故取其信号波形幅度即可作为方位探边地质信号.在不同电阻率的地层中,波形基值不同,表明其对地层电阻率敏感,故可将其用于反映地层电阻率.
2.2 DWPR地质信号响应
由式(28)、(29)可知,将仪器旋转测量所得信号经一阶、二阶三角函数拟合,得到原始信号波形幅度,作为仪器方位探边信号,如图5所示.
由图5可知,208.28 cm、243.84 cm地质信号在地层边界处达到极值;且从高阻层入低阻层时,信号为正值,从低阻层入高阻层时信号为负值.即208.28 cm、243.84 cm地质信号准确反映了地层边界位置及方位信息.
为对比单斜线圈系与双斜线圈系地质信号响应特征,建立两层地层模型,其电阻率为100 Ωm和1 Ωm,线圈系源距均为243.84 cm,频率为100 kHz,以89°倾角由100 Ωm地层穿过1 Ωm地层,其幅度原始信号与幅度比地质信号响应如图6所示.
由图6a可知,仪器靠近界面时,单斜线圈系与双斜线圈系幅度原始信号波形幅度均增大,在界面处达到最大值.将原始信号处理为地质信号,并以0.02 dB为门槛值,如图6b所示,单斜线圈系幅度比地质信号探测距离为6.19 m,双斜线圈系幅度比地质信号探测距离为6.8 m.由此可说明,双斜线圈系具有比单斜线圈系更突出的探边距离.
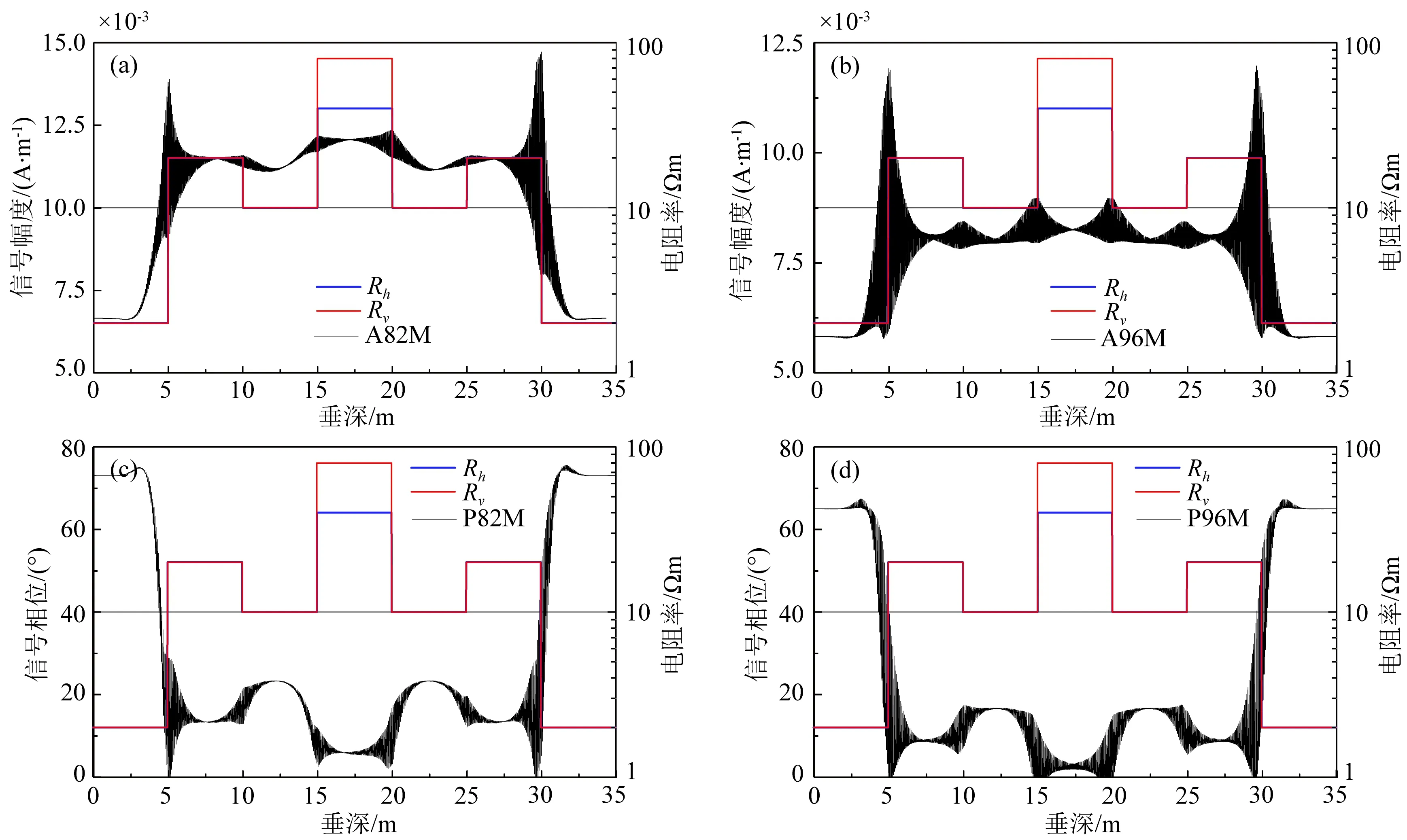
图4 208.28 cm、243.84 cm线圈系信号响应Fig.4 The responses of receivers at 208.28 cm and 243.84 cm spacing
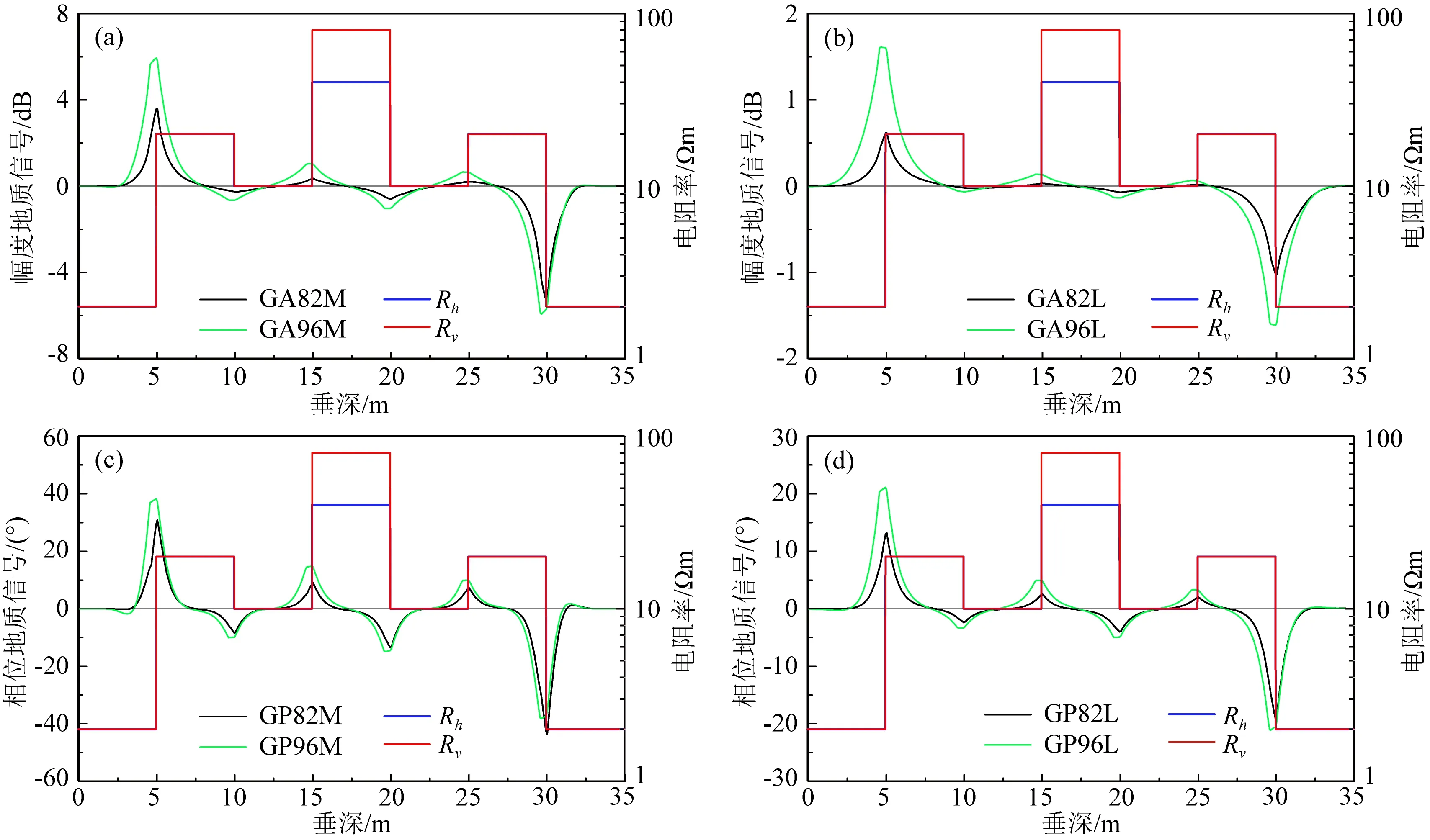
图5 208.28 cm、243.84 cm线圈系地质信号响应Fig.5 The geo-signal of receivers at 208.28 cm and 243.84 cm spacing
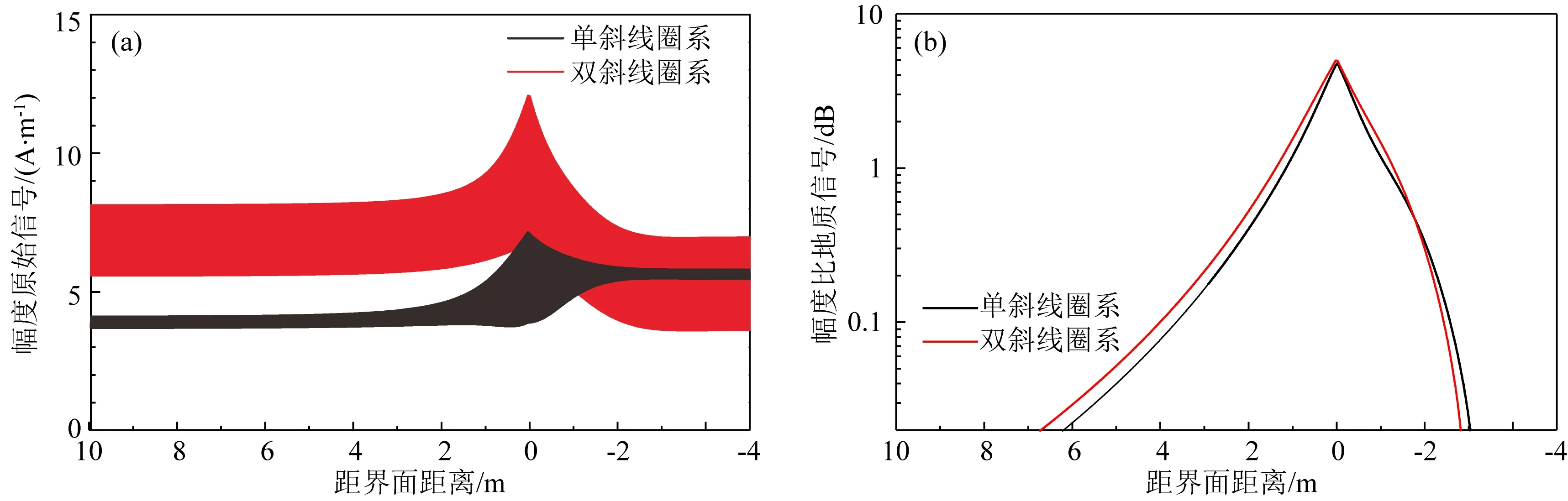
图6 单斜线圈系与双斜线圈系响应特征对比Fig.6 The responses comparison between monoclinc coils and biclinc coils
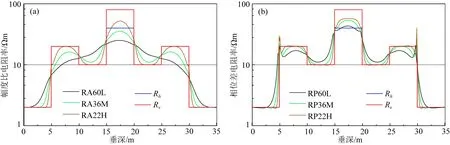
图7 55.88 cm、91.44 cm、152.4 cm线圈系电阻率信号响应Fig.7 The apparent resistivity of receivers at 55.88 cm, 91.44 cm and 152.4 cm spacing
2.3 DWPR电阻率信号响应
由式(28)可知,仪器旋转均匀采样,取均值后即为zz分量;将对应相位差、幅度比刻度,仪器可得55.88 cm、91.44 cm、152.4 cm三种尺寸、三种频率的相位差、幅度比电阻率信号,如图7所示.
由图7可知,电阻率信号RA22H、RA36M、RA60L、RP22H、RP36H、RP60L(R代表电阻率;A、P分别代表幅度比、相位差;22、36、60代表源距;H、M、L分别代表高频、中频、低频,即2 MHz、400 kHz、100 kHz)均反映了地层电性特征.同尺寸下,相位差电阻率比幅度比电阻率更易受地层边界影响,其在界面处犄角更明显.相较于相位差电阻率,幅度比电阻率探测深度更大,反映地层宏观电阻率.而相位差电阻率分辨率更高,对地层电阻率反映更接近真值.
3 应用实例
将收敛递推算法应用于随钻方位电磁波测井仪器电阻率刻度与地质信号验证,以物理实验角度证明算法及仪器响应的准确性;将算法应用于实时地质导向,则可证明算法的实用性与可靠性.
3.1 地质信号验证
地质信号验证实验实照如图8所示,仪器水平放置于玻璃钢架,地面以水泥胶结厚0.5 cm的铝板,每转动仪器22.5°后静止采样20 min,测量一周后可得地质信号.调整仪器距地面高度后,可得不同高度下的地质信号,如图9所示,为仪器距地面1.16 m、0.76 m、0.36 m的仪器响应与正演响应对比图.

图8 地质信号验证实验Fig.8 Geo-signal verification test
由图9可知,仪器从距铝板2.5 m处往铝板移动时地质信号增大,在距铝板约0.63 m时达到最大值,继续往铝板移动时地质信号减小.实测信号与正演响应信号对应良好,只在高度为0.76 m的位置信号略有误差.该次实验证明了算法正演响应与仪器地质信号实测响应的正确性.
3.2 电阻率信号验证
为验证随钻方位电磁波测井电阻率信号,将仪器置于直径4 m、高9.5 m的大型NaCl溶液罐中(图10所示),为减小外界环境影响,罐体外围采用玻璃钢架.通过调整NaCl浓度可改变溶液电阻率,从而模拟不同导电能力地层.图11对比了仪器实测电阻率信号与正演电阻率刻度图版,可以看出二者吻合,实现了正演计算和仪器性能的相互验证.
3.3 随钻地质导向实例
进一步将正演算法应用于随钻方位电磁波测井资料处理,图12为渤海某井DWPR仪器实时反演结果.图中,第一道为伽马曲线,第二道为深度道,第三道为电阻率曲线,第四道为伽马成像,第五道为井眼轨迹及反演窗帘图.
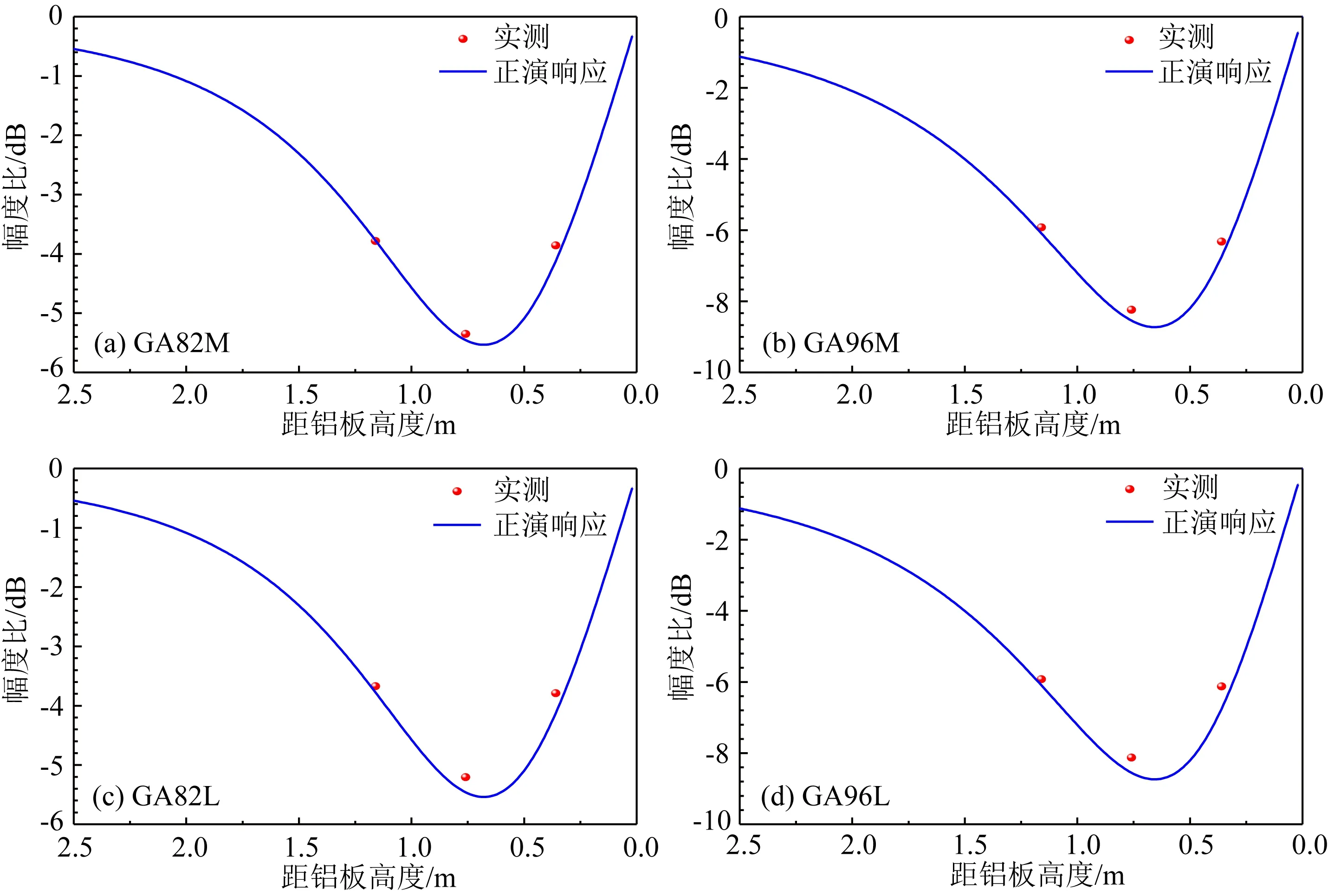
图9 208.28 cm、243.84 cm方位信号验证Fig.9 The results of 208.28 cm and 243.84 cm geo-signal verification

图10 电阻率信号验证环境Fig.10 The environment of apparent resistivity verification
根据邻井对比,该井目的层下部存在水淹,在水平段导向过程中,为确保后期投产效果,控制在储层中上部钻进,保证油柱高度.根据电阻率反演剖面判断,储层横向变化较大,层界面沿井轨迹方向呈现“凹”字形,先下倾后上倾,局部倾角达到2.5°,与地震剖面地层整体下倾的趋势有所区别.测深2218 m(位置4),垂深1505.63 m,井斜88.70°,根据测井显示,电阻率已升高至10 Ωm以上,目的层物性变好,但探边显示储层顶界面继续下倾,目前轨迹已紧贴顶界面,为防止钻出储层,降斜至87.5°钻进.测深2258 m(位置5),垂深1506.95 m,井斜87.41°,据探边显示,距顶界面约2 m,顶界面下倾趋势变缓,储层横向展布变化,地层变厚,下界面(水淹层界面)超出探边探测范围,判断形成锥状水淹,水淹层界面非均匀推进,增斜至89°钻进.实钻过程中的认识调整井斜角度,寻找优质储层,至测深2448 m(位置8)处成功完钻.实时导向过程中,仪器电阻率信号、方位信号响应稳定,搭载本快速正演算法的反演剖面清晰、稳定,体现了仪器响应及算法的正确性和高效性.
4 结论
本文基于赫兹势函数法求解水平层状各向异性介质中的电磁场,通过引入地层界面,提取并消除溢出因子,可解决各向异性介质全场张量响应解析解中的数值溢出问题.介绍并分析了国产DWPR仪器设计原理及其地层边界探测性能.真实作业环境中DWPR仪器地质导向结果证明了基于本文算法的资料快速处理软件具有稳定性和高效性.
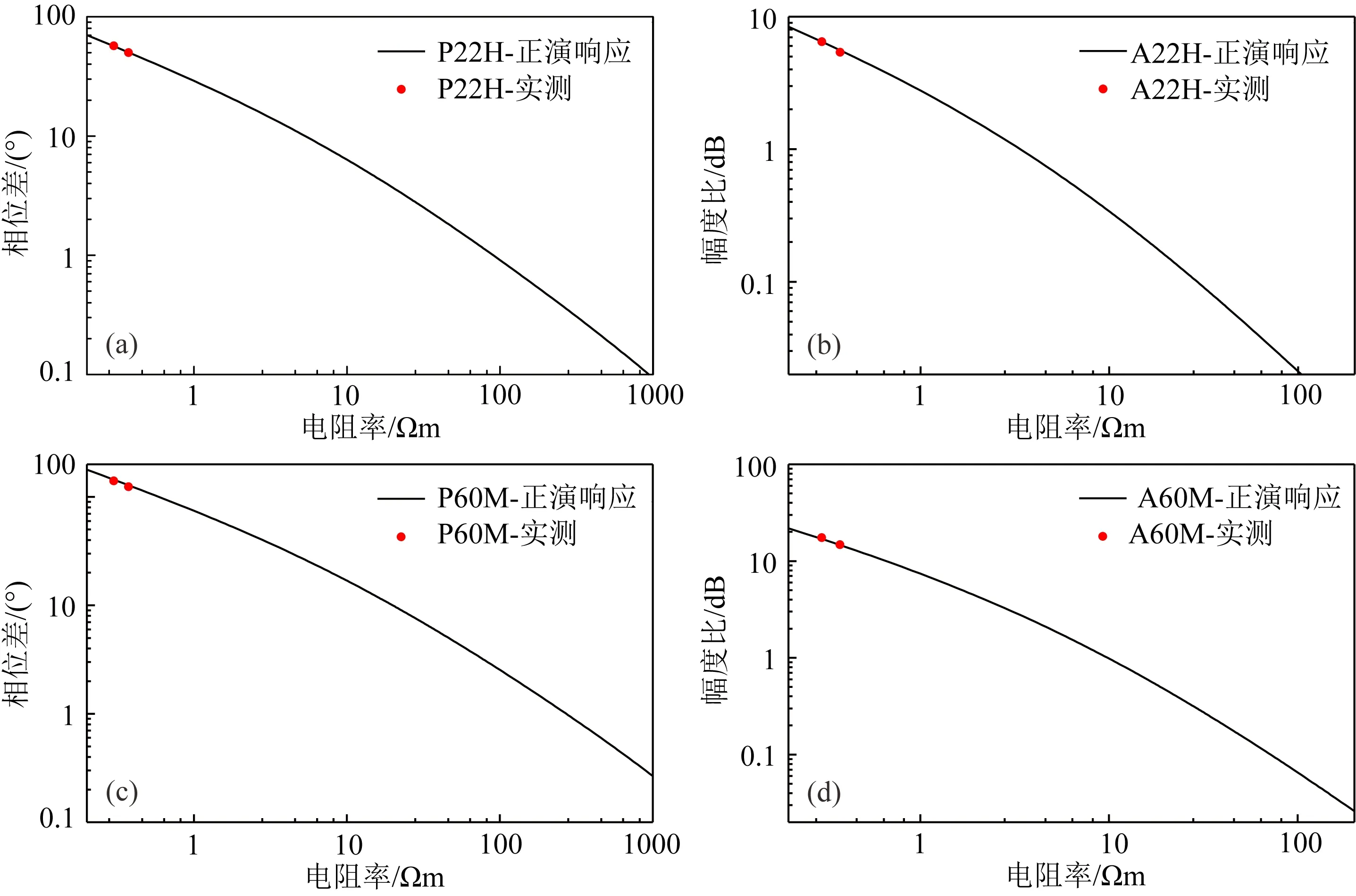
图11 55.88 cm、152.4 cm电阻率信号验证Fig.11 The results of 55.88 cm and 152.4 cm apparent resistivity verification
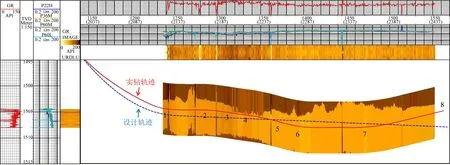
图12 渤海某井随钻地质导向实时反演结果Fig.12 The real-time geo-steering inversion in Bohai base
附录A
令:
(A1)
(A2)
可得:
(A3)
(A4)
(A5)
(A6)
(A7)
(A8)

AN、B1、PN、Q1、SN和T1表达式已知后,第i层中的系数Ai、Bi、Pi、Qi、Si和Ti表达式可根据系数递推式推导,从而可获得各层中场的表达式.
