基于深度学习的位场边界识别方法

张志厚， 姚禹， 石泽玉， 王虎， 乔中坤， 王生仁，覃礼貌， 杜世回， 罗锋， 刘慰心

1 西南交通大学地球科学与环境工程学院， 成都 611756 2 西南交通大学， 高速铁路线路工程教育部重点实验室， 成都 610031 3 吉林大学地球探测科学与信息技术， 长春 130026 4 中铁一院勘察设计院集团有限公司， 西安 710043

0 引言

高精度的位场(重力、磁力)勘探被广泛应用于矿产资源勘察(Kamm et al., 2015; Krahenbuhl and Li, 2017; Liu et al., 2017)、岩石结构探测(Prutkin and Saleh, 2009; Astort et al., 2019)、水文地质勘察(Williams and Stevens, 2002)、环境地质调查(Zunino et al., 2009; Gavazzi et al., 2016; Yannah et al., 2019)、地质体定位(Beiki et al., 2012; Tang et al., 2018; Hu et al., 2019)、油气资源远景评价(Gadirov et al., 2018)等.位场的边界识别可为地质体解译提供更加丰富的信息.地质体的边界通常是指构造界线，不同岩性不同地质体的接触线，其物理性质表现为具有一定密度或磁性差异的边缘位置(王万银, 2010).位场边界识别方法主要有数值计算和数理统计两大类方法，两类方法针对不同深度不同姿态目标体的边界识别(Cordell，1979；王万银，2010; Wang et al., 2010; Sertcelik and Kafadar, 2012; 马国庆等, 2012; Ma, 2013; Ma et al., 2015; Zhou et al., 2013; Beiki et al., 2014; Yuan et al., 2014; Hidalgo-Gato and Barbosa, 2015; Yuan and Yu, 2015; 颜廷杰等, 2016; 周帅等, 2016; 于平等, 2019; 汤井田等, 2019; 郭华等, 2019)都取得了一些较好的应用效果.以上方法的主要思路是对位场数据进行各类型基本运算，然后研究其最大值、零值与地质体边界之间的对应关系.这些计算方法都属于无监督式的机器运算，其计算结果精度与目标体空间分布有一定的关联性，因此在实际应用中，选择适合的边界识别方法，才能获得可靠的结果.

近年来，大数据已渗透到诸多行业里，已成为社会发展的重要生产要素和战略资源.人工智能(Artificial Intelligence, AI)、机器学习(Machine Learning，ML)和深度学习(Deep Learning,DL)等已成为许多领域科学家和工程师关注的热点，地球物理领域也不例外.诸多ML方法在地球物理的数据分析与处理中(Guo et al., 2011; Sun and Li, 2015; Jiang et al., 2016; Nawaz and Curtis, 2019; Xie et al., 2019；刘昊楠等；2020；王昊等，2020)都表现出较好的优势.ML属于AI的领域，它是通过统计计算从大数据中提取相关特征.其优势是计算速度快，精度高；其挑战是需要获取足够的样本数据和优化相关参数(Kim and Nakata, 2018).DL(LeCun et al., 2015; Schmidhuber, 2015)作为ML的一个重要新分支，在语音和图像的识别与分类中取得了超越性进展(Russakovsky et al., 2015; Greenspan et al., 2016; Davoudi et al., 2019; Pan et al., 2019; Schoppe et al., 2020)，其标志着ML的里程碑.尤其是自2012年ImageNet大赛上，AlexNet架构的DL网络结构以极大的优势获得图像分类的冠军(Krizhevsky et al., 2012)，卷积神经网络(Convolutional neural networks, CNN)模型开始受到计算机视觉领域的广泛关注.CNN能够从大量的监督样本中自动学习到由底层位置特征到高层属性特征的层次化特征表达，避免了人工特征设计的弊端，极大地增强了模型的泛化能力，已经在地球物理资料自动解译方面取得了巨大的突破(Xiong et al., 2018; Li et al., 2019; Shi et al., 2019; Wu et al., 2019; Zhang et al., 2020a).

以上针对地球物理资料自动解译的DL模型框架是通过修改CNN网络结构，实现了“端到端”训练和预测，其实质上属于DL语义分割框架的方法.Long等(2015)将CNN中的全连接层替换为卷积层，提出了一种全卷积深度神经网络(Fully Convolutional Networks, FCN)模型，并成功地应用于医学图像语义分割(Russakovsky et al., 2015)，实现了高精度的类别解释.但是同时该网络模型也引入了两个问题，一是池化等下采样步骤提取深层属性特征时容易显著降低特征数据的分辨率，从而导致最终上采样得到的预测结果严重损失局部细节信息，因此不能对异常体边界等细节做出精细化的表达；二是卷积通过一定大小的感受野只能利用局部信息，缺少全局信息的辅助，容易造成局部目标体预测混淆，最终结果不连续且包含一定的椒盐噪声(乔文凡等, 2018).基于以上问题，许多学者提出了金字塔解析网络结构(Zhao et al., 2017)、SegNet网络结构(Badrinarayanan et al., 2017)、U-Net网络结构(Ronneberger et al., 2015)和DeepLab系列网络结构(Chen et al., 2018)等进行了改善，这些网络结构及其改善策略也极大地促进了FCN方法在地球物理反演问题求解中的研究与应用，如井地电磁二维反演(Puzyrev, 2019)、直流电阻率反演(Liu et al., 2020)、速度模型重建(Li et al., 2020a)、重力异常和重力张量异常联合反演(张志厚等, 2021a)、以及磁异常和磁梯度异常联合反演(张志厚等, 2021b)等.虽然基于经典FCN网络结构在地球物理模型语义分割中都取得了令人满意的结果，但仍然存在对细小异常体边界分割不够精细的情况，如密集细小的次生断裂，岩性差异较小的界限等.为了进一步提高FCN的预测精度，在计算机视觉领域，相关研究者分别采用密集连接网络(Zhou et al., 2020)、多尺度渐进融合网络(Xian et al., 2020)、自适应阈值多模型融合网络(Jiang et al., 2020)和注意机制密集连接网络(Xia et al., 2021)等进行了图像高层特征的提取，实现了不同场景下图像的精细化表达.这些研究为本文重磁位场边界识别带来了更为广泛的应用前景.

基于此，本文提出了位场边界识别的DL方法，DL网络结构为一种融合多尺度特征的注意机制与密集跳跃连接网络，称为PFD-Net(Potential Field Detection-Net).PFD-Net首先是在基于改进的U-Net网络结构中嵌套标准卷积模块(Standard Convolution Modules, SCM)和密集跳跃连接模块(Dense Skip Connections Modules，DSCM)；然后通过注意模块(Attention Module, AM)融合不同大小的低层、高层特征，形成以U-Net网络为骨干的DSCM和AM网络结构；此外，相较于网络结构的精心设计而言，网络结构充分学习所依赖的训练样本数据同样值得关注，其多样性与足量性的快速构建决定了方法的实用性，本文采用张志厚等(2021a, b)提出的基于网格点几何格架的位场空间域快速正演算法进行高效构建.最后，对本文所提方法进行理论数据和实测数据的检验，以此来证实的文中方法的可行性和有效性.

1 边界识别方法

1.1 CNN网络结构与语义分割

地下半空间存在的异常体(或边界)会在观测面上引起位场响应，不同异常体(或边界)引起的位场响应也表现出不同特征.即具有一定的空间相关性和局部存在性.总之，位场数据的输入和输出有两个特点：(1)空间的对应性；(2)局部的存在性(张志厚等, 2021a,b).而CNN方法正是通过卷积算子重点学习输入图像与输出标签的局部性和空间性(Shi et al., 2019)，如提取图像的边界信息(Deng et al., 2012)等.此外，小子域滤波器法(Jiang and Gao, 2012)(该滤波器由较多卷积算子的串联组成)的成功应用也表明了通过卷积算子识别位场边界的可行性.

CNN网络结构是由一系列不同尺度的卷积算子和相关滤波器组成，卷积算子的主要功能提取输入数据或者中间结果的特征，每一层卷积计算公式为(Li et al., 2019)：

(1)

典型的CNN网络结构包含了卷积运算、非线性激活、层间批处理归一化、池化操作以及节点丢弃等.每一层的输出构成了下一层的输入，重复这些步骤可以堆叠一个较深的网络结构，因此称为深度神经网络.网络节点超参数(如卷积核，偏置项等)是通过监督学习和反向传播进行更新.优化算法通常采用随机梯度下降法、以及适合大数据量且具备计算效率高收敛速度快的RMSProp算法和ADAM算法等.随着训练轮数的增加，超参数的更新，使得网络输出与标签的误差逐渐减小，最终获得了训练数据到标签数据的复杂非线性映射关系.

CNN方法典型应用于分类(预测类别标签)任务，即输出是一个单一的热点向量，表明该图像属于某一类的可能性.然而，一些任务中，如图像分割(Shi et al., 2019; Davoudi et al., 2019; Pan et al., 2019; Schoppe et al., 2020)，不仅需要对图像进行分类，而且还要进行超像素分类(图1a).本文也将位场的边界识别视为语义分割任务，即将位场的数据作为输入端，输出端分为边界位置与非边界位置两类进行监督学习(图1b).FCN(Shi et al., 2019)方法作为CNN典型分支可实现密集像素预测，可生成任意大小的分割图像，并且计算速度快，成为当下最为先进和流行的语义分割方法.随后，较为典型的FCN网络结构，如U-Net(Ronneberger et al., 2015)、SegNet(Badrinarayanan et al., 2017)和DeconvNet(Noh et al., 2015)都出色地完成了相关语义分割任务.并且适用于地球物理数据解译分割和地球物理数据端到端反演的网络结构大都是在以上网络结构基础上的改进(Li et al., 2019, 2020a; Wu et al., 2019; Xiong et al., 2018; Shi et al., 2019; Puzyrev, 2019; Liu et al., 2020; 张志厚等, 2021a,b)，此类改进网络都属于编码器-解码器的CNN网络结构，图1c为典型的编解码器CNN网络结构示意图.

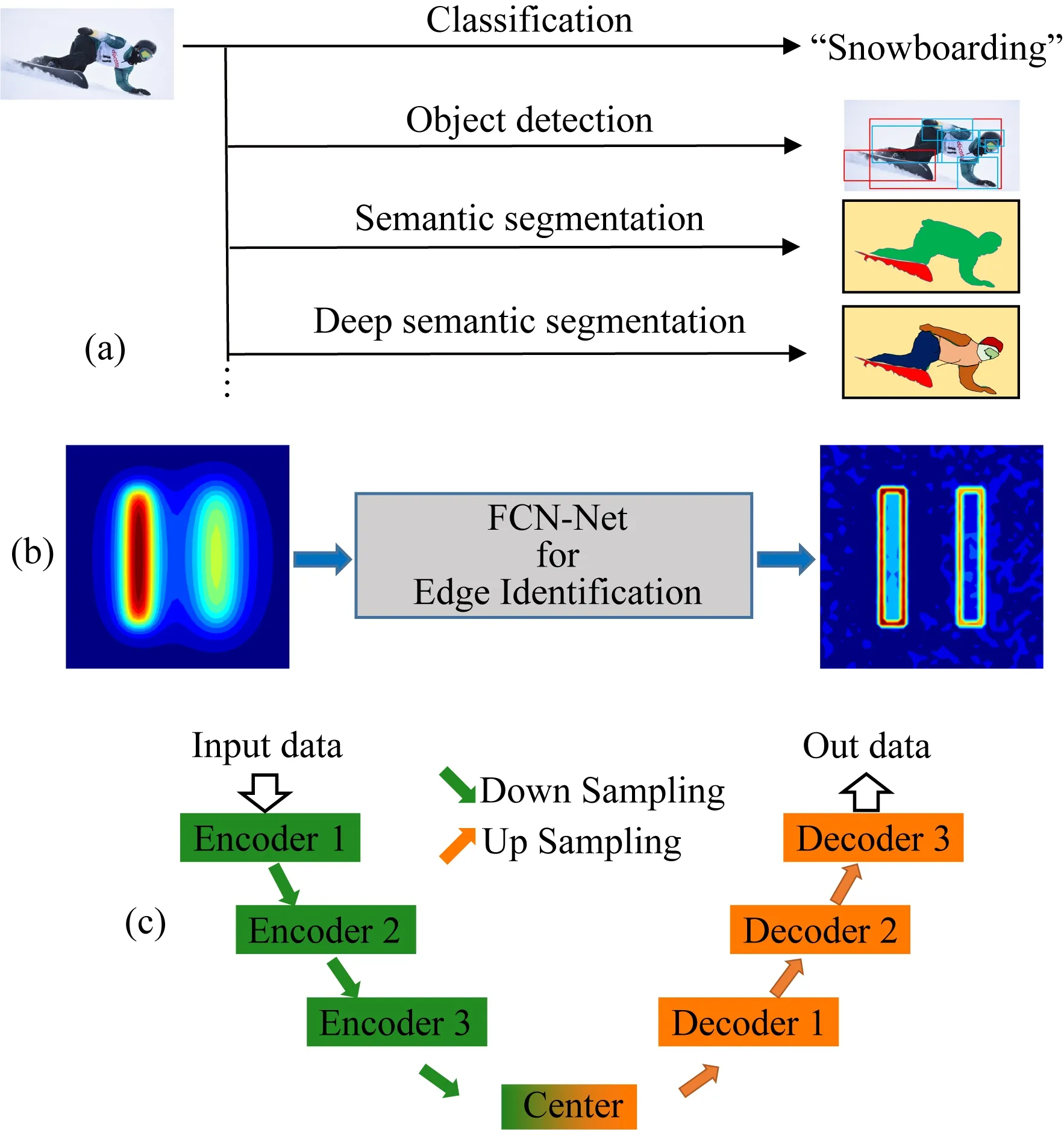
图1 CNN端到端示意图 (a) 图像语义分割； (b) 位场数据通过FCN预测边界位置； (c) 典型的编解码CNN网络结构.Fig.1 Schematic diagram of CNN end-to-end (a) Image semantic segmentation; (b) Edge detection based on potential field data in FCN; (c) Typical CODEC in CNN.

1.2 PFD-Net网络结构

为了进一步提高位场边界细节的识别精度，本文提出了一种名为PFD-Net的网络结构，其流程图如图2所示，该网络结构采用改进的U-Net作为骨干网，包含了SCM、DSCM、AM等模块，以及用于信息融合的相关连接.主干网络通过4个尺度的下采样来提取特征，而密集跳跃连接则充分利用不同尺度的特征进行组合.注意模块通过高级特征加权初始低级特征，以对密集边界进行精准识别.

图2 位场边界识别PFD-Net总体结构图Fig.2 Schematic diagram of potential field edge detection PFD-Net

本文基于改进的U-Net(Badrinarayanan et al., 2017)结构作为PFD-Net结构的骨干网络，如图3所示.该骨干网络是U-Net网络结构的一个简化，其包含一个获取地质特征的收缩路径和一个用于向上采样的对称扩展路径，以此实现精准定位.并采用基于最大池化和反卷积的收缩-扩展结构.当给定一个固定大小的卷积核(大小为3×3)，网络结构的有效感受野随着网络层数的增加而增大.随着网络深度的增加，左侧路径的通道数从16个变为256.通过跳跃层，将右侧路径上的局部、浅层特征映射与左侧路径上的全局、深层特征映射相结合.SCM各层间采用批处理归一化(Puzyrev, 2019)增加网络训练的稳定性，激活函数选用DL类型最常用的线性整流函数ReLU(Xu et al., 2015)来提高训练的收敛性，编码阶段的各卷积层之间加入Dropout层(Hinton et al., 2012)来增强网络结构的泛化能力，最后通过1×1的卷积之后再采用Sigmoid(Badrinarayanan et al., 2017)激活函数进行输出.

骨干网络结构是对原始U-Net网络结构进行了三个方面的修改：一是输入数据不是RGB三色通道的像素值，而是每一个观测点的位场响应值；二是简化了网络结构的深度及卷积通道数，这是由于本文的目标仅仅是两个类别的语义分割，其复杂度远低于多类别分割任务，所以不太适用太深的网格数和太多的卷积通道数；三是地质体边界所对应的标签不全是封闭的曲线，也不是语义分割区块，而是与地质体边界对应的曲线段，其可能不封闭.

图3 骨干网络结构—改进的U-Net 由4个下采样层和4个上采样层组成，下采样和左侧卷积层对应编码阶段，上采样和右侧卷积层对应解码阶段，图中黑色数字表示特征图的通道数，红色数字表示单通道数据的大小，Conv为卷积，ReLU为激活函数，Sigmoid为输出激活函数，MaxPool为最大池化，Up-Conv为上采样和卷积 Dropout为丢弃节点，BN为批处理 归一化，Copy & Concatenate为复制跳跃链接.Fig.3 Backbone network structure——the improved U-Net It consists of four down-sampling layers and four up-sampling layers. The down-sampling layers and the left convolution layers correspond to the coding stage, and the up-sampling layers and the right convolution layers correspond to the decodingstage.The black numbers in the Figure indicate the number of channels in the feature map, and the red numbers indicate the size of single channel data, Conv is the convolution, ReLU is the activation function, Sigmoid is the output activation function, MaxPool is the maximum pooling, Up-Conv is the up-sampling and convolution, Dropout is discarding node, BN is batch normalization, Copy & Concatenate is the copy skip link.

图4为PFD-Net网络的拓扑结构.文中将网络结构中包含1层深度U-Net和1个AM的网络结构称为PFD-Net-L1(图4a)，类似的有PFD-Net-L2(图4a)和PFD-Net-L4(图4b)等.为了便于绘图，用Xij代替图4中的标准卷积模块.图4b中所示的PFD-Net-L4是以U-Net网络结构为基础骨干网络，其中节点X1,1到节点X5,1为编码结构，节点X5,1到节点X1,5为解码结构.首先在改进的U-Net基础上，增加了6个节点(X1,2、X1,3、X1,4、X2,2、X2,3、X3,2)放在不同的尺度上；其次，对所有节点输出的特征进行密集跳跃连接；第三，在同一层编解码器上添加注意机制模块，其输入为相邻层的节点Xi,1和Xi+1,5-i；最后，对第一层输出的各个节点与AM的合成结果进行输出，从而得到最终的语义分割结果.

1.3 密集跳跃连接

经典U-Net是将编码阶段高分辨率特征与解码阶段上采样特征进行融合，该方式是一种浅层信息融合，未将深层信息充分利用，造成编解码器之间存在语义鸿沟(邢妍妍等，2020).因此，有必要将深层信息上采样融合浅层信息或者将浅层信息下采样融合深层信息，从而可以加强编解码器之间的语义联系，提升模型的性能.本文重新设计的PFD-Net是在编码器的高分辨率特征与解码器相应的丰富语义特征合并之前捕获背景对象的细粒度细节.同时，密集跳跃连接路径重用不同层的特征作为输入，并连接不同深度的网络特征层，其目的是缩小语义鸿沟，从而使得编码特征和相应解码特征在语义上相似时，分割效果得到了极大的改善.

PFD-Net的密集跳跃连接由多个SCM和上采样模块组成，SCM和跳跃路径是核心之一.通过嵌套的密集跳跃连接，每个SCM的输入为同一层先前所有卷积输出和下一层上采样到同一级联层输出的串联结果，这种方式有助于恢复下采样引起的信息丢失，并使所有层信息在网络中充分传播.图5所示为密集跳跃连接的结构，可以看出，在节点X1,1和X1,5之间加入了三个SCM，每一个SCM都有一个连接层，它都融合了同层以前的卷积输出和下一层SCM的上采样输出.融合后模块输出继续与下一层相对应模块上采样特征再融合，如此迭代直至下一层没有对应的上采样模块.每一模块的输出结果为：

图4 PFD-Net网络结构 (a) PFD-Net-L1和PFD-Net-L2； (b) PFD-Net-L4.Fig.4 PFD-Net network structure

图5 密集跳跃连接结构 Conv为卷积，BN为批处理归一化，ReLU为激活函数，Dropout为 丢弃节点，Up-Conv为上采样和卷积，Skip Connections为跳跃连接.Fig.5 Dense skip connection structure Conv is convolution, BN is batch normalization, ReLU is activation function, Dropout is discard node, Up-Conv is up-sampling and convolution.

(2)

式中，Xi,j表示当前特征提取模块的输出，i(i=1、2…5)表示编码器下采样的索引，j为同一层模块序号，也是跳跃连接路径的索引序号，C(·)表示特征提取的卷积操作，U(·)表示上采样操作，[·]表示特征通道连接.

因此，PFD-Net整体特征融合结构呈倒金字塔形，每一层都包含了密集模块，通过密集跳跃连接(图5)将编码阶段提取的特征向后传递并深度融合，缩短编解码语义鸿沟，提升模型的学习能力.同时，密集跳跃连接可以充分有效组合网络模型中各深度层的大量特征，提高预测精度.此外，密集跳跃连接可以有效地减少梯度消失(Xia et al., 2021).

1.4 注意力机制

密集跳跃连接通过编码器的浅层信息和下一层的高级特征来重建细节信息.然而，这种设计没有考虑特征的多样性和全局的信息，可能会导致边缘细节信息不完全一致(Xia et al., 2021).注意力机制是一种能够突出关键特征点的算法，机器学习的注意模块可以对数据中的特征信息进行重点提取，区分主次信息，削弱消除背景噪声等无用信息，使得输入数据的特征得以有效利用(Zhang et al., 2020b).图6给出了本文注意模块网络结构，该模块将全局平均池化应用于高层特征层，并利用高层特征为低层特征提供加权指导(Li et al., 2018).因此，注意模块能够增强解码器上采样过程中高层特征权重系数的影响，并有效地利用金字塔结构的多尺度特征映射，从而提高目标区域的像素级分类精度.

图6 全局注意力的上采样模块结构 Conv为卷积，ReLU为激活函数，Global Pooling 为全局池化，BN为批处理归一化.Fig.6 Global attention upsample module structure Conv is convolution, ReLU is activation function and BN is batch normalization.

2 模型试验

2.1 样本数据集及训练

DL学习样本数据主要来自于真实数据和人工合成数据.相关学者探索了基于精细化标注真实数据训练的语义分割模型(Bai et al., 2017)，然而真实样本数据标注耗时、昂贵，且对人为错误敏感；人工合成方法可以获取大量的数样本数据，足量代表性数据可极大提高训练模型的泛化性能，如在深度学习的重磁反演(张志厚等, 2021a，b)、电磁反演(Puzyrev, 2019; Li et al., 2020b)、直流电阻率反演(Liu et al., 2020)、地震反演(Li et al., 2020b)中取得了较理想的成果.因此，本文通过正演计算来获取样本数据集.模型试验是将地下半空间划分为31×31×15个长方体单元，其中长方体单元大小为100 m×100 m×50 m，模拟观测数据区大小为3.1 km×3.1 km.坐标系采用笛卡尔坐标系，z轴向下，计算水平面位场数据的个数为32×32个，即采样数据点为地下半空间网格点在水平面的投影.因此，样本输入数据的大小为32×32个，样本标签数据个数也为32×32个.每一个标签数据是由多个长方体单元组成模型边界在水平面上的投影线，标注为“1”，非边界位置标注为“0”.文中将长方体位置设置于地下半空间的非边缘区域，与文献(张志厚等, 2021a, b)中长方体单元组合类似，其具体如下：I型：1×1×1块体(均匀抽样4761对)；II型：2×2×2块体(3388对)；III型：4×4×4块体(4000对)；IV型：6×6×6块体(1944对)；V型：8×8×8块体(512对).各模型块体剩余密度为1 g·cm-3，或者剩余磁化强度大小为1.0 A·m-1.为了便于计算及分析，磁场正演计算所采用的地磁场与剩磁异常体的磁化倾角和偏角都一致，其中磁化倾角为90°，偏角为0°.通过正演获得的位场(重力异常或磁异常)样本数据对个数为14605对.由于重磁位场的正演为线性关系(张志厚等, 2021a,b)，故可利用已正演的样本数据进行不同物性大小的样本数据扩充，扩充后的样本数据为29210对.将样本数据划分为训练数据、测试数据以及验证数据，其对应比为18∶1∶1，即训练数据集包含26452个样本数据，验证集和测试集各有1460个样本数据.训练轮数为100，每次训练后进行一次验证，训练误差为L2范数，其表达式为：

(3)

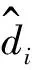
图7 PFD-Net训练误差及验证误差Fig.7 Training error and validation error of PFD-Net

2.2 组合模型边界识别

采用了四组长方体模型(图8a、b、c、d)对本文所提方法进行检验.模型一、模型二和模型三在地下空间位置及物性参数如表1所示，模型四为图8h中白色折线与x轴、y轴所围成的近似上三角块体，块体厚度为0.5 km，块体的中心深度为0.55 km，块体密度为1 g·cm-3.通过正演获得模型一、二、三、四的重力异常或磁异常分别如图8e、f、g、h所示.

表1 长方体模型参数Table 1 Cuboid model parameters

利用文中已训练完成的PFD-Net网络分别对四组模型对应的位场数据进行边界识别，其结果分别如图9a、b、c、d所示.同时为了更加贴合实际资料处理，对位场数据分别加入其最大值10%的随机噪声(图8i、j、k、l)，再对四组模型进行边界识别，结果分别如图9e、f、g、h所示.此外，对四组模型的正演数据及其含噪声数据分别采用总水平导数法(Total Horizontal Derivative, THDR)(Cordell, 1979)、加强解析信号倾斜角法(Enhanced Analytic Signal Tilt Angle, EASTA)(颜廷杰等，2016)以及基于三维构造张量的两种归一化反正切滤波器方法(Normalization Structural Tensor Edge Detection, NSED; Normalization Vertical Derivative Structural Tensor Edge Detection, NVSED)(周帅等，2016)进行边界识别，以此来对比本文所提方法的效果.THDR、EASTA、NSED及NVSED的识别结果分别如图10、11、12、13所示.

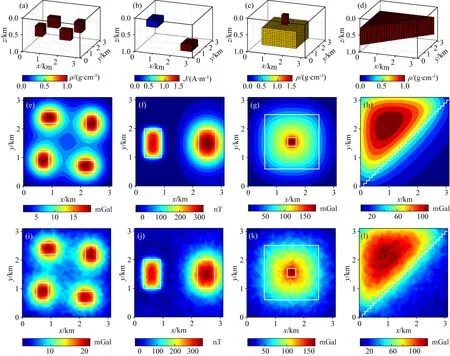
图8 三维模型透视图及正演结果 (a)、(b)、(c)、(d)分别为四种模型的三维透视图；(e)、(f)、(g)、(h)分别为(a)、(b)、(c)、(d)图中模型对应的正演数据； (i)、(j)、(k)、(l)分别为(e)、(f)、(g)、(h)正演的加噪声数据；图中白线为模型对应的水平边界位置.Fig.8 Perspective drawing of three-dimensional model and forward calculation (a),(b),(c) and (d) Correspond to perspective drawing of four kinds of three-dimensional model respectively; (e),(f),(g) and (h) Correspond to forward calculation data of (a),(b),(c) and (d) respectively; (i),(j),(k) and (l) are the noise-contained forward calculation data of (e),(f),(g) and (h) respectively; White line in the Figure is the horizontal boundary position of the model.

图9 四种模型边界识别结果 (a)、(b)、(c)、(d)分别为四种模型正演数据采用文中方法的边界识别结果；(e)、(f)、(g)、(h)分别为相对应加噪声数据 采用文中方法的边界识别结果.Fig.9 Forward data and edge detection result of four kinds of models (a),(b),(c) and (d) Correspond to edge detection result of forward calculation data of model one, two, three and four with PFD-Net; (e),(f),(g) and (h) Correspond to edge detection result of noise-contained forward calculation data of model one, two, three and four with PFD-Net.

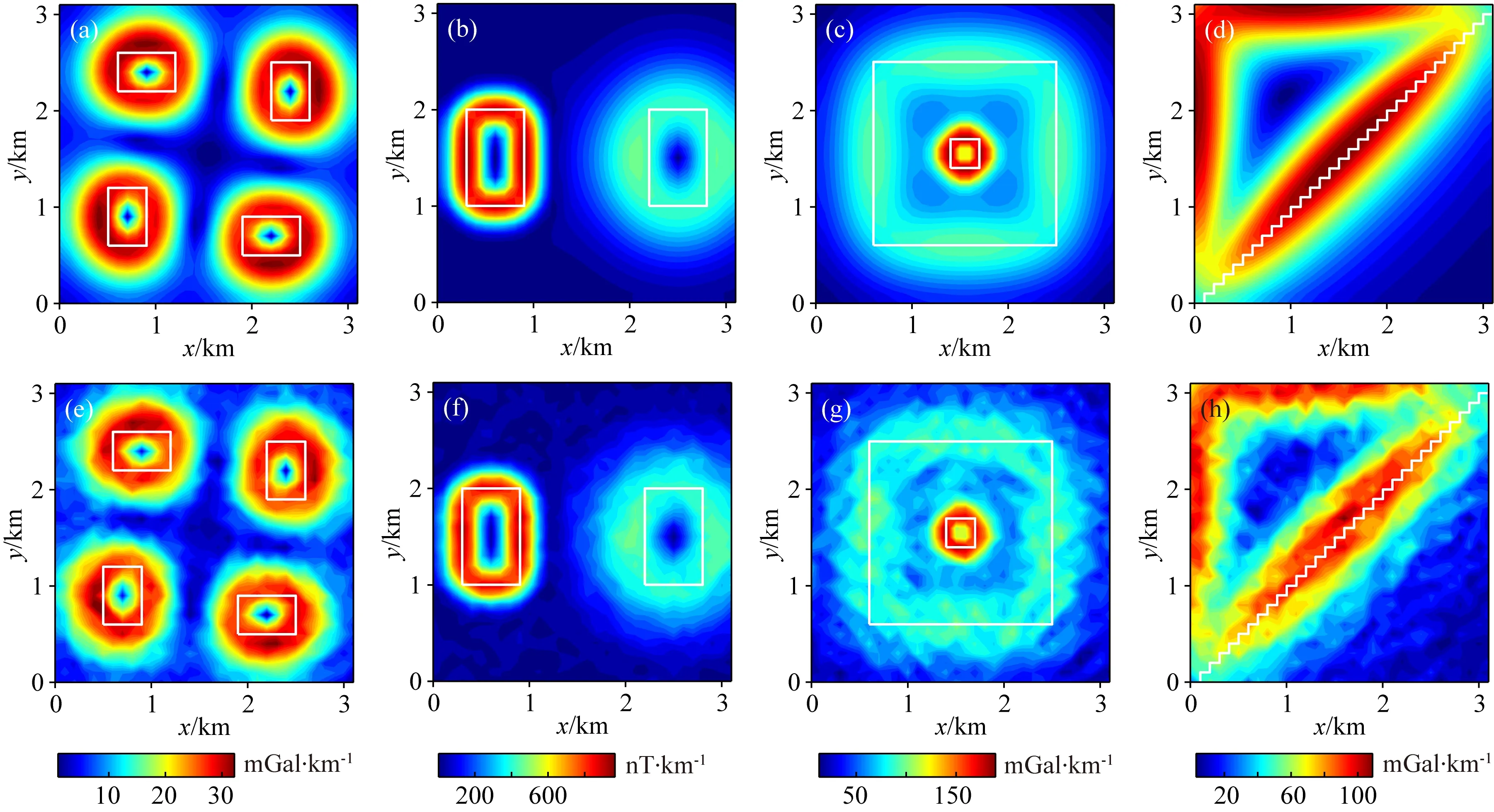
图10 THDR识别结果 (a)、(b)、(c)、(d)分别为模型一、二、三、四正演数据的THDR边界识别结果； (e)、(f)、(g)、(h)分别为四种模型正演加噪数据THDR的 边界识别结果；图中白线为模型对应的水平边界位置.Fig.10 Edge detection result of THDR (a),(b),(c) and (d) Correspond to edge detection result of forward calculation data of model one, two, three and four with THDR; (e),(f),(g) and (h) Correspond to edge detection result of noise-contained forward calculation data of model one, two, three and four with THDR; White line in the Figure is the horizontal boundary position of the model.

图11 EASTA识别结果 (a)、(b)、(c)、(d)分别为模型一、二、三、四正演数据的EASTA边界识别结果； (e)、(f)、(g)、(h)分别为四种模型正演加噪数据EASTA的 边界识别结果；图中白线为模型对应的水平边界位置.Fig.11 Edge detection result of EASTA (a),(b),(c) and (d) Correspond to edge detection result of forward calculation data of model one, two, three and four with EASTA; (e),(f),(g) and (h) Correspond to edge detection result of noise-contained forward calculation data of model one, two, three and four with EASTA; White line in the Figure is the horizontal boundary position of the model.

图12 NSED识别结果 (a)、(b)、(c)、(d)分别为模型一、二、三、四正演数据的NSED边界识别结果； (e)、(f)、(g)、(h)分别为四种模型正演加噪数据NSED的 边界识别结果；图中白线为模型对应的水平边界位置.Fig.12 Edge detection result of NSED (a),(b),(c) and (d) Correspond to edge detection result of forward calculation data of model one, two, three and four with NSED; (e),(f),(g) and (h) Correspond to edge detection result of noise-contained forward calculation data of model one, two, three and four with NSED; White line in the Figure is the horizontal boundary position of the model.

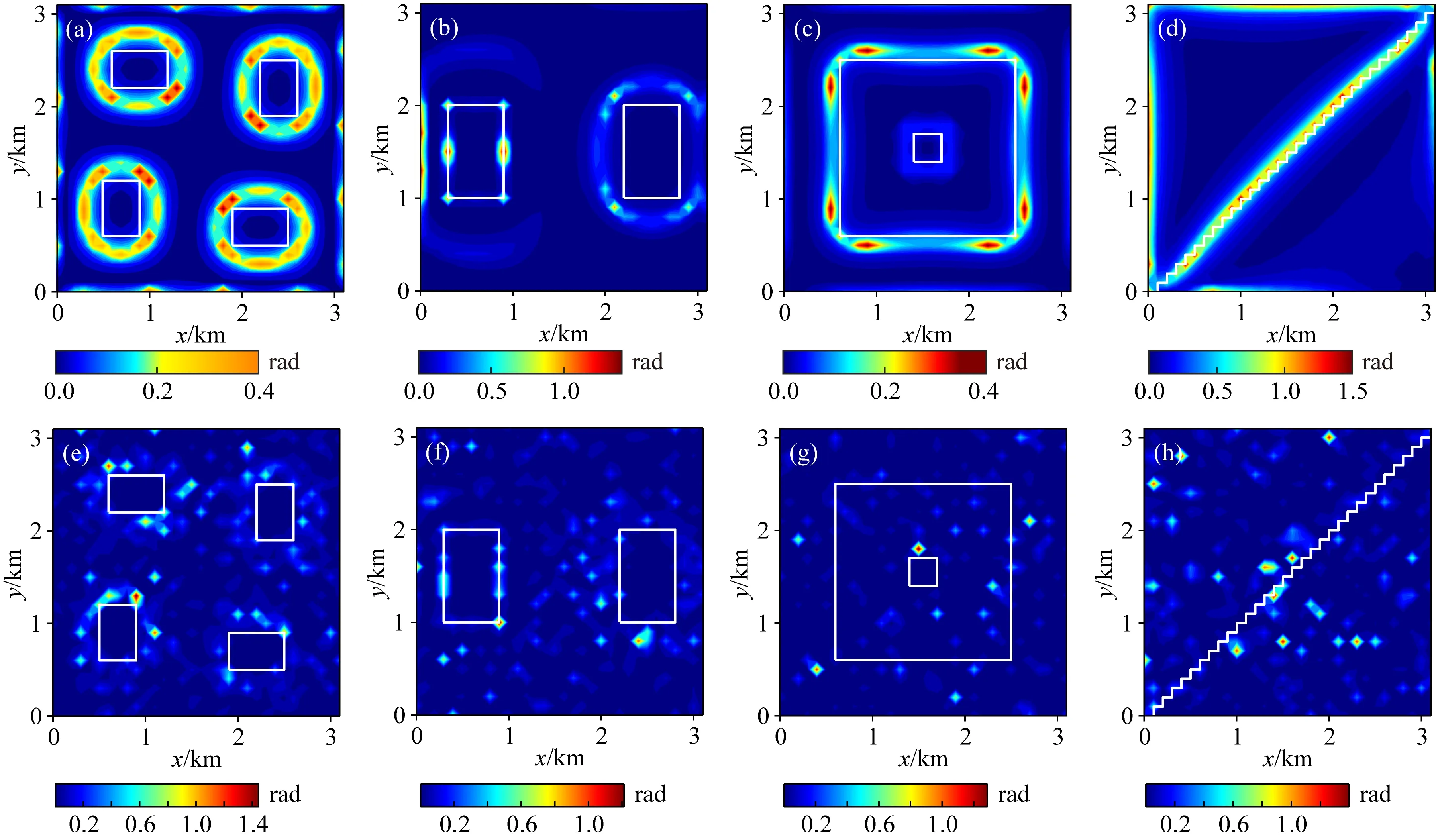
图13 NVSED识别结果 (a)、(b)、(c)、(d)分别为模型一、二、三、四正演数据的NVSED边界识别结果； (e)、(f)、(g)、(h)分别为四种模型正演加噪数据NVSED的 边界识别结果；图中白线为模型对应的水平边界位置.Fig.13 Edge detection result of NVSED (a),(b),(c) and (d) Correspond to edge detection result of forward calculation data of model one, two, three and four with NVSED; (e),(f),(g) and (h) Correspond to edge detection result of noise-contained forward calculation data of model one, two, three and four with NVSED; White line in the Figure is the horizontal boundary position of the model.

(1)模型一

模型一由四个大小相同、埋深相同、剩余密度相同的异常体组成(图8a)，其在水平面投影的边界如图8e中白色线段所示.从图9a、e可以看出无论是无噪声重力异常还是加噪数据的PFD-Net识别结果都与地质体边界相吻合，相比THDR(图10a、e)、EASTA(图11a、e)、NSED(图12a、e)及NVSED(图13a、e)的识别结果，本文方法精度更高，其计算结果都“聚焦”于真实边界处，尤其是在含噪声情况下，EASTA(图11e)和NVSED(图13e)受噪声影响较大，本文方法的鲁棒性更强.表明本文PFD-Net网络不仅可以有效的对地质体边界位置进行准确识别，而且对单一块体模型所构建的样本数据集进行训练，可对类似块体的组合模型进行边界位置预测，相应数值检验结果也验证了理论上CNN卷积核具有局部性和权值共享的特点和优势，也表明了本文PFD-Net网络所具备的泛化性能.

(2)模型二

模型二由两个大小相同、埋深不同、剩余磁化强度不同的磁性异常体组成(图8b)，两个异常体在水平方向上有一定距离，其在水平面投影的边界如图8f中白色线段所示.该模型无噪声数据的PFD-Net识别结果(图9b)与地质体的边界一致，浅部异常体识别结果相比深部异常体识别结果较好，两异常体临边位置识别效果稍差.但相比其他四种方法(THDR、EASTA、NSED及NVSED)对不同深度组合模型的识别结果(图10b、11b、12b、13b)，PFD-Net方法识别精度最优，尤其是深部异常体水平边界的刻画也更加精确.

含噪声数据的识别结果(图9f)相比无噪声数据的识别结果较差，尤其是深部异常体的结果不够清晰，具体表现在某些边界位置变宽，但并不影响识别效果.相比其他四种方法(THDR、EASTA、NSED及NVSED的识别结果(图10f、11f、12f、13f))，PFD-Net方法仍然具备识别的准确性.表明本文PFD-Net网络的抑制噪声能力强.

此外，本文PFD-Net对浅部异常体的识别精度相比深部异常体识别精度高的原因可能如下：大小相同、物性相同的模型在不同埋深处的位场异常存在较大的差异，而模型在水平面投影的边界位置相同，即样本数据存在位场响应相差较大，但其对应的标签却一样.因此，训练的网络在具备泛化性能的同时也必须具备一定的容错性，该容错性是导致深部异常体识别精度稍逊的原因之一.

(3)模型三

模型三为两个大小不同、埋深不同、剩余密度不同，但水平中心位置相同的异常体组成(图8c)，两个异常体在垂直方向上相连，其在水平面投影的边界如图8g中白色线段所示.从图9c可以看出，在无噪声情况下，除去浅部异常体附近的干扰，其余部分识别效果较好；含噪声情况下，深部异常体的三个边部虽有影响(图9g)，但并不影响整体的识别效果，其在异常体边界部分的定位是极为准确的，并且浅部异常体的识别精度未降低.说明了本文PFD-Net对深大异常体及其上部的浅小异常体都具有一定的识别能力.

无噪声情况下，其余四种方法也较好地识别出“浅小深大”的组合模型边界(图10c、11c、12c、13c)，虽然NVSED方法也表现出较高的识别精度(图13c)，但并没有本文所提方法的精度高(图9c).含噪声情况下，THDR(图10g)和NSED(图12g)的识别精度降低，EASTA(图11g)和NVSED(图13g)受噪声影响较大，识别能力显著下降，而本文所提方法具有较强的稳定性(图9g).

(4)模型四

图8d所示为模型四的三维透视图，图8h为模型四的边界水平投影及正演位场数据.可以看出无噪声数据的识别结果在中间部分的识别精度较高，与理论模型轮廓保持高度一致，在白色曲折线段的首尾部分对应的边界识别结果与理论模型轮廓存在一定的差异(图9d).该差异并不能说明PFD-Net的识别效果在边部稍差，恰恰相反能够说明本文所提方法具备较强泛化性与高精度性.这是由于在异常体角点处能够识别单一块体位场响应数据一是不完整，二是整个模型并不是标准的台阶模型，而是近似上三角块体.同理，在x轴和y轴附近也存在一定识别结果.图9h为含噪声数据的识别结果，识别精度没有明显下降，表明本文PFD-Net识别精度高且具有较好的稳定性.

相比其他方法，无噪声情况下NVSED方法的识别结果相对较好(图13d)，其识别效果与本文所提方法相近，但在含噪声情况下，NVSED的识别效果较差(图13h)，EASTA同样也受到噪声的影响较大(图11h)，THDR(图10d、h)、EASTA(图11d)和NSED(图12d、h)的识别结果除去边部和拐角的影响，也能准确的识别出边界的位置.但总体而言，本文所提方法无论是在识别精度还是稳定性上都优于其他四种方法.

2.3 未化极磁性体模型边界识别

为了检验本文PFD-Net对未化极磁性体的边界识别效果，需要先构建不同磁化倾角和磁化偏角的样本数据集，样本数据集类型如前文所述的4个类型(I型、II型、III型和IV型)，然后训练PFD-Net再进行边界预测.检验模型如图14所示，由三个长方体模型组合而成，长方体相关参加见表2，将磁化倾角分别设计为60°和30°两种情况进行检验.文中正演了两种不同磁化倾角下组合磁性模型体的理论异常(图15a、e)，以及加入理论异常最大值5%的随机噪声(图15c、g)，图15a、c、e、g对应的识别结果如图15b、d、f、h所示.看出未化极理论磁异常数据以及加噪数据的识别结果都与地质体边界相吻合，尤其是含噪数据的识别结果也具有较好的稳健性.表明了本文PFD-Net网络同样适用于未化极磁异常的边界识别.

图14 磁性体三维模型透视图Fig.14 3D perspective view of the magnetic body model

表2 未化极磁性体模型参数Table 2 Model parameters of unpolarized magnetic body

3 实际资料应用

采用本文的方法对藏东南某铁路隧道西段的航空磁测数据进行边界识别.藏东南某隧道西段长达近20 km，大致位于念青唐古拉山脉东段与喜马拉雅东构造结北部前缘交会区域.该部位为典型的高山峡谷地貌：一是海拔高差大，从平均约2000 m跨度到约4500 m(图16a)；二是雅鲁藏布江及其支流的快速下切和广泛分布的冰川剥蚀作用共同造就了深切峡谷的发育.构造框架方面，该隧道位于冈底斯岩浆弧地层，隧道西段洞身段岩性主要为燕山期片麻岩、片麻状二长花岗岩、花岗岩等侵入岩体，局部夹有一些变质岩捕虏体；隧道出口地层为白垩系大理岩夹变钙质砂岩、变基性火成岩；隧道北侧出露地层为泥盆系-石炭系大理岩，以及大理岩夹变钙质砂岩，该套地层与下覆燕山期片麻状二长花岗岩呈不整合接触(图16a)(罗锋等，2021).另外，隧道还穿过嘉黎—察隅构造混杂岩带，可见碎裂岩、断层角砾岩，局部发育有构造蚀变岩.总体而言，该段落由于印度板块与欧亚板块在喜马拉雅东构造地区的陆-陆碰撞及碰撞后的持续向北推移和楔入作用，导致断层变形历史和破裂样式异常复杂及地层单元和岩性特征多变性，再受到高山峡谷型地表过程的叠加效应，难以在该地区直接有效地开展相关地质单元和构造界限的野外判别.

航磁原始数据经过校正、调平、化极以及网格化后的结果如图16b所示，图中观测区的大小为19.8 km×3.1 km，数据点距为100 m×100 m，共199×32个点.从图16b中可以看出测区中西部异常呈近似北西向条带状分布，有一定的连续性.整个测区在局部都存在磁异常封闭圈，可能表明存在花岗岩等侵入岩体，或者为变质岩捕虏体.

图15 未化极磁性体模型检验效果 (a)、(e)分别对应磁化倾角为60°与30°的正演磁异常；(c)、(g)分别为(a)、(e)对应的加噪声数据；(a)、(c)、(e)、(g)对应的 识别结果为(b)、(d)、(f)、(h)；图中白线为模型对应的水平边界位置.Fig.15 Test effect of unpolarized magnetic model (a) and (e) Correspond to forward calculation magnetic anomalies with magnetization inclination angles of 60°and 30° respectively; (c) and (g) are the noise-contained data correspond to (a) and (e); (b),(d),(f) and (h) are the recognition results corresponding to (a),(c),(e) and (g); White line in the Figure is the horizontal boundary of the model.

图16 藏东南某铁路隧道西段地质地形图(a)、航磁异常(b)和本文方法的识别结果(c)Fig.16 Geological topographic map of the western section of a certain railway tunnel in southeastern Tibet (a), aeromagnetic anomalies (b), and the detection results of this method (c)

PFD-Net网络输入与输出大小为32×32，不能直接对任意大小的实际资料直接预测，需要先将实际资料切割为若干个与训练网络大小一致的数据，然后分别预测再合成为最终结果.本文为了避免因边界的特征提取问题而产生拼接痕迹，继而影响最终的识别效果，采用了滑动切割方法对网格化原始数据进行裁剪，滑动点距为16个点，切割窗口大小为32×32，共切割13个数据块.文中将13个数据块分别采用PFD-Net网络进行识别，重复区域进行融合处理，最终获得的结果如图16c所示.从图16c可以看出，局部明显存在封闭块体，识别封闭线大于0.4的块体多达13处，这与测区存在的花岗岩侵入体或变质岩捕虏体有较强的联系.根据识别结果可进一步解译出两条东西走向的界线，南侧界线与广义的嘉黎断裂剪切带具有较好的一致性，北侧界线可能为不同岩性的接触带.另外，一些近南北向展布的异常界线，也与该部位发育的系列南北向小规模断层具有较好的匹配性.由此可见，即便是针对具备复杂地质地貌环境的目标区，本文所采用的PFD-Net算法仍能够较好地用于解译构造迹线和岩性迹线，并且解译结果具有较好的可信度.

4 结论与讨论

本文提出了一种融合多尺度全局注意力机制和密集跳跃连接的DL网络结构—PFD-Net，并用于位场的边界识别.该网络以U-Net为骨干网络，加入了密集跳跃连接和对应的标准卷积模块，从位场数据中提取异常体的边界特征.此外，全局注意力模块对提取的低高层特征进行分离和融合，作为多维度的输入，使得网络更具鲁棒性.相比经典的U-Net网络结构，本文所提网络结构大大提高了预测精度.

文中通过四组模型试验来检测本文所提方法效果：(1)对单一块体模型所构建的样本数据集进行训练，可对类似块体的组合模型进行边界识别，表明了本文PFD-Net网络所具备的泛化性能；(2)相同标签不同输入的样本数据对，会增加网络结构训练的复杂度，并可能会导致深部异常体预测精度下降，但不影响整体的识别效果；(3)对垂直方向分布大小差异较大的异常体仍具有一定的识别效果；(4)含噪声情况下，PFD-Net网络的识别精度并没有明显下降，表明本文所提方法具有一定的稳定性.另外，将文中的方法应用于藏东南某铁路隧道西段的航空磁测数据的边界识别，其结果与已知的地质情况基本吻合，表明本文的反演方法具有较好的可信度.

本文所提的位场边界识别方法实质上是利用CNN方法对地下异常体的水平位置进行分类及回归预测，相比基于DL的重磁异常及其梯度异常反演，有很大的不同之处在于样本数据的标签.物性反演所需样本数据的标签是异常体的位置向量，不仅仅具有方向性，且具有物性大小值，其有效标注数据量大.而边界识别所需样本数据的标签是异常体在水平面上投影边界所组成的向量，但该向量只具有方向性，且标注的数据个数少.此外，边界识别的样本数据存在不同输入数据但标签数据相同，由于地球物理存在多解性，位场边界识别方法需具有的普适性在于如何构建一个足量的、多样性的、代表性的高质量样本数据集.然而，这势必会引起网络复杂度与计算量增加.因此，在下一步工作中，我们将进一步增加样本的多样性和改进样本数据的标注方法来提升复杂地质模型的识别效果，同时在保证实验准确性的情况下，进一步更好地简化和压缩模型，提高网络训练的速度和效率，从而使得基于DL的位场数据处理方法更加普适化与智能化.

致谢非常感谢匿名审稿专家对论文提出的宝贵修改建议！