利用K-SVD字典学习算法压制海洋大地电磁噪声
2022-05-05封常青李予国吴云具段双敏
封常青, 李予国,2,3*, 吴云具, 段双敏,2
1 中国海洋大学海洋地球科学学院, 青岛 266100 2 中国海洋大学海底科学与探测技术教育部重点实验室, 青岛 266100 3 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266237
0 引言
大地电磁法(Magnetotelluric, MT)是一种以天然电磁场为场源来研究地球内部电性结构的地球物理方法.海洋大地电磁测深(Marine MT)通过坐底式海底电磁采集站(OBEM)测量感应电磁场.高导电的海水相当于一个低通滤波器,在一定程度上可以减少人类活动所形成的各类人文噪声,使得海底成为一个低噪声的电磁环境(Jones, 1999).然而,由于引力、地球自转、空气流动等作用,海水处于不停的运动之中,且其运动形式多种多样(如海浪、潮汐和洋流等).海水的运动会对海洋大地电磁探测尤其是浅水区电磁探测产生严重干扰.一方面,位于海底的电磁接收仪器易受到海水冲刷作用而发生振动(Lezaeta et al., 2005).另一方面,根据法拉第电磁感应定律,运动的海水如海浪(Weaver, 1965; Fraser, 1966)和潮汐(Larsen, 1968)等因切割地磁场而产生感应电流,进而产生二次感应磁场.它们都会对所采集电磁数据的质量产生影响,降低海洋MT数据的信噪比.
在浅水环境中,海浪运动产生的感应电磁场是影响海洋电磁数据质量的主要噪声之一(Lilley et al., 2004).海浪波动所产生的磁感应强度通常为几纳特到十几纳特,电场强度为几至几十微伏每米(Chave, 1983).海浪运动对电磁场的影响主要出现在1~30 s的周期范围内,导致此频段内MT数据信噪比降低,视电阻率和相位曲线发生严重畸变(Duan et al., 2020).根据海浪感应电磁场的特性,可以采用信噪分离算法提取海浪感应电磁场.于彩霞等(2010)和张宝强(2018)分别将经验模态分解和小波阈值去噪方法应用到浅水区MT数据处理中,视电阻率曲线得到明显改善,但相位效果不理想.
K-SVD字典学习方法作为一种成熟的稀疏表示算法已经被成功地应用于图像去噪(Elad and Aharon, 2006)、语音信号增强(Wang et al., 2016)和地震勘探中随机噪声压制(Tang et al., 2012)等领域.字典学习算法在电磁数据去噪中也得到初步应用.汤井田等(2018)基于人文噪声的特点,利用字典学习算法构建过完备字典,分离音频大地电磁数据中的人文噪声.Xue等(2020)将K-SVD字典学习方法应用于时间域航空电磁数据去噪处理中,取得了较好效果.字典学习算法在大地电磁信号(Li et al., 2020, 2021b)和可控源电磁信号(Li et al., 2021a)噪声压制中也得到了应用.海浪运动会对浅水区大地电磁磁场数据造成严重干扰(Constable et al., 1998).考虑到海浪感应磁场的窄带谱特性,以及其在时间域表现出较强的规律性(张宝强, 2018).我们使用K-SVD字典学习方法提取海浪感应磁噪声,并结合视电阻率信息进行相位校正,期望提高海洋大地电磁数据的质量.
在本文中,我们首先阐述K-SVD字典学习方法与相位校正的基本原理,其次提出海浪感应磁噪声去噪流程.然后分别将该方法应用于仿真数据和南黄海实测大地电磁数据噪声抑制中,并分析其效果.
1 海浪感应磁噪声压制方法
1.1 K-SVD字典学习方法
在信号处理领域,某些信号经过合适的变换后,可以用一个仅含有少量非零元素的矩阵进行表示,即信号在变换域中是稀疏的.在稀疏表示算法中,这种变换域被称为“字典”,其列向量则被称为“原子”.从综合角度来看,信号可以表示为少量字典原子的线性组合,即信号在字典表示下是稀疏的(练秋生等, 2015).
假设一维离散信号为y∈M,并可以表示为
y=Dx+ε,
(1)
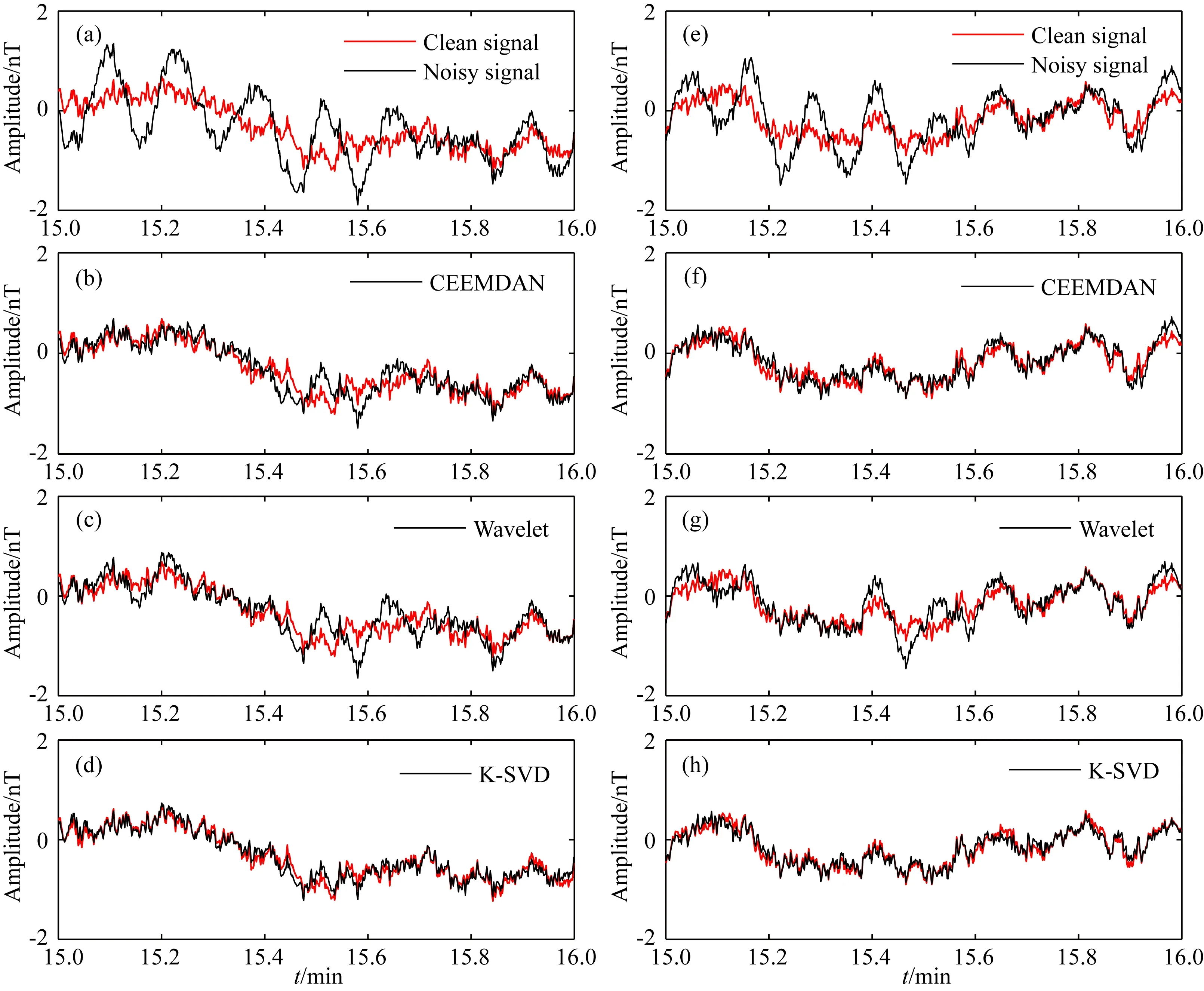
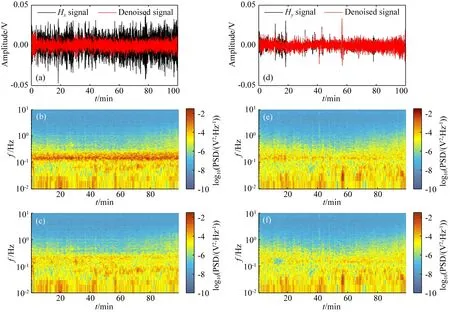
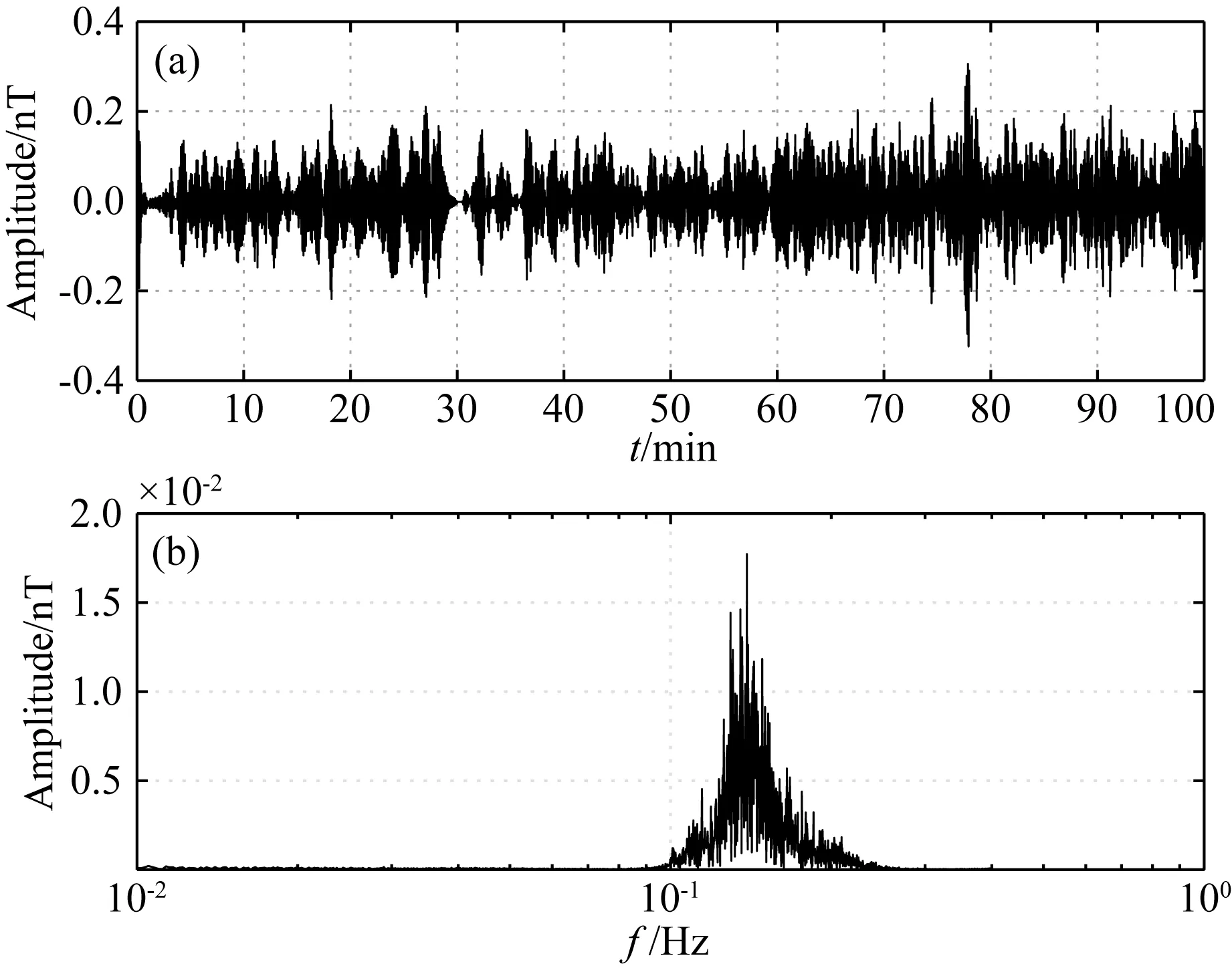
式中,x∈K是稀疏的系数矩阵,D∈M×K称为字典,这里M和K分别为字典D的行数和列数.字典D通常是过完备字典,即M (2) 式中,‖x‖0是x的l0范数,它表示x中非零元素的数量,ε为残差阈值. 在字典D给定的情况下,Mallat和Zhang(1993)采用匹配追踪算法(Matching Pursuit, MP)求解稀疏系数x.Pati等(1993)用正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)求解过完备字典下的稀疏表示问题.传统的匹配追踪算法在求解稀疏系数时,往往通过事先定义某种数学变换或调和分析方法构造过完备字典,例如过完备离散余弦变换(Overcomplete Discrete Cosine Transform, ODCT)字典.虽然该类算法在构造字典时相对简单,但是受限于原子固定的形状,它对信号的适应性较差.为了提高字典对信号的适用性,Aharon等(2006)和Rubinstein等(2008)提出了K-SVD字典学习方法.该方法采用数据驱动方式直接从训练集中获得与目标信号特征相符合的原子,使得更新后的字典对目标信号具有更好的适应性. 对于训练信号集Y=[y1,y2,…,yN]∈M×N,假设其每一列信号均可以表示为字典D中少量原子的线性组合,则稀疏表示问题可以写成为 (3) 利用K-SVD字典学习方法求解(3)式的过程可分为稀疏编码和字典更新两个阶段,二者交替进行.在稀疏编码阶段,采用正交匹配追踪算法获得稀疏系数矩阵X=[x1,x2,…,xN]∈K×N,在字典更新阶段则利用奇异值分解(Singular Value Decomposition, SVD)方法依次对字典D逐列进行更新.我们期望在更新第k列原子时,(4)式取最小值(Aharon et al., 2006): (4) (5) 定义Ωk∈N×|ωk|,其中在(ωk(i),i)处元素值为1,其余位置元素值为0.式(4)可以等价为 (6) 下面,举例说明稀疏表示方法消除信号噪声的原理及效果.我们模拟一段多频信号: T=sin(2π×100t+0.1)+3cos(2π×130t+0.9) +0.7sin(2π×170t+1.5). (7) 图1 不同噪声增益系数S的重构信号信噪比 当噪声增益系数S=1.02时,去噪后的 重构信号信噪比达到极值13.14 dB.Fig.1 SNR of reconstructed signals with different noise gain coefficient S When S=1.02, the SNR of the reconstructed signal reaches the extreme value of 13.14 dB. 对模拟得到的信号加入高斯白噪声后得到信噪比为0 dB的加噪信号.分别对无噪信号、高斯白噪声和加噪信号以不同的噪声增益系数S进行OMP稀疏表示,重构信号的信噪比随噪声增益系数的变化曲线如图1所示.由图1可以看出,在重构信号信噪比相同的情况下,无噪信号所使用的噪声增益系数比高斯白噪声的更大,这说明在相同字典的情况下,噪声信号更难以表达.这就是稀疏表示算法可以用于信号去噪的本质.而由加噪信号的重构结果可以看出,过小或过大的噪声增益系数均不能实现最佳去噪效果,存在最优的噪声增益系数使得重构信号的信噪比取得极值.在实际去噪实验中,最优的噪声增益系数具有未知性.在去噪过程中,通常通过试验不同的增益系数,并结合去噪后信号的时频信息(如振幅谱、时频图等)确定最优噪声增益系数. 在利用K-SVD字典学习方法实现信噪分离后,对去噪后的信号进行Robust阻抗估计往往可以得到较为光滑的视电阻率曲线,但是所得到的相位曲线仍然显得不够理想.Weidelt(1972)、陈乐寿和王天生(1985)论述了大地电磁阻抗视电阻率与相位之间的转换关系.基于该转换关系可以实现相位曲线和视电阻率曲线的相互校正(刘建利, 2013; 杨生等, 2001).因此,我们可以基于校正后的视电阻率信息对相位进行再校正.在一维情况下,大地电磁阻抗视电阻率和相位之间的转换关系可以表示为(陈乐寿和王天生, 1985): (8) 其中,φ(f)为相位,z(g)为阻抗振幅,这里f和g为频率.由式(8),可以得到下列近似表达式(陈乐寿和王天生, 1985): (9) (9)式为视电阻率ρa(f)和相位φ(f)之间的转换关系式.该关系式虽然是在一维地电条件下导出的,但它在非一维地电条件下亦基本成立(杨生等, 2001). 用差分近似式(9)中的微分,可得: (10) 利用上式便可以实现基于视电阻率信息的相位校正. 海浪感应磁噪声压制与相位校正的主要步骤如下: (1)由于训练字典过程中的输入信号为二维训练信号集,所以需将滤波后的一维时间序列按一定步长进行分段,并将分段信号作为二维矩阵的列向量进行组合; (2)设置初始字典D为ODCT字典,利用正交匹配追踪算法对二维训练集进行稀疏表示,获得稀疏系数矩阵X; (3)利用K-SVD字典学习算法更新字典D; (4)重复步骤(2)和(3),在满足迭代条件后,利用更新的字典DK-SVD和稀疏矩阵XK-SVD重构海浪感应磁噪声; (5)对去噪后的MT数据进行Robust阻抗估计,并结合视电阻率信息进行相位校正. 综上所述,海浪感应磁噪声压制与相位校正流程如图2所示. 图2 海浪感应磁噪声压制与相位校正流程图Fig.2 Flow chart of wave-induced magnetic noise reduction and phase correction 采用模拟数据检验本文方法抑制海浪感应磁噪声的效果.为此,首先分别模拟海洋大地电磁信号时间序列和海浪感应磁场时间序列.其次,将大地电磁水平磁场分量和海浪感应磁噪声叠加获得含噪信号,然后再利用K-SVD方法进行噪声压制,并与自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)(Torres et al., 2011; Colominas et al., 2014)和小波阈值去噪(张宝强, 2018)方法的处理结果进行对比.最后对去噪后的电磁数据进行Robust阻抗估计,并计算视电阻率和相位. 利用构造系统函数法模拟大地电磁数据,构造系统函数可以表示为(Loddo et al., 2002): (11) 式中,K1为比例系数,Ri为零点,Pi为极点(i=1,2,3,4).考虑到海水具有低通滤波的特性,为得到符合海洋大地电磁场特性的时间序列,经过测试实验,本文选取的系数如下: K1=0.1; R1=0.01,R2=1.05,R3=10.0,R4=15.0; P1=-0.01,P2=-7.0,P3=-10.0,P4=-2.0. (12) 利用式(11)计算得到MT磁场信号的单边谱,再将它扩展为双边谱.然后利用逆傅里叶变换,可得到MT磁信号时间序列.在阻抗Z(ω)已知的情况下,再利用阻抗关系式E(ω)=Z(ω)H(ω)便可以计算得到电场的频谱序列.对电场频谱序列进行逆傅里叶变换得到电场时间序列. 为了获得海洋大地电磁模拟数据,设计如图3所示两个一维地电模型并进行正演计算,将得到的阻抗作为阻抗张量矩阵的非对角线元素.利用合成的阻抗张量矩阵可以得到四个电磁场水平分量的时间序列(汤井田等, 2013; 张宝强等, 2018).假定采样频率为10 Hz,采样时长为1 h.利用上述方法得到的海洋大地电磁四个水平分量的时间序列如图4所示. 图3 两个一维水平层状地电模型 (a) 用于模拟Ex与Hy分量; (b) 用于模拟Ey与Hx分量.Fig.3 Two 1-D horizontal layered geoelectric models (a) Used to simulate the Ex and Hy components; (b) Used to simulate the Ey and Hx components. 图4 模拟得到的四分量海洋大地电磁数据 (a),(b) 电场水平分量时间序列; (c),(d) 磁场水平分量时间序列.Fig.4 Simulated marine MT data (a),(b) Time series of horizontal components of electric field; (c),(d) Time series of horizontal components of magnetic field. 根据法拉第电磁感应定律,海浪切割地磁场会产生感应电流,从而产生二次感应磁场.海浪运动感应电场E和磁感应强度B满足下列麦克斯韦方程组: (13) 其中,电流密度J=σmE+σmV×(F+B),σm为介质电导率,V为海浪运动速度,F为地磁场.由于B远小于F,故电流密度可以近似为J=σm(E+V×F).海浪感应电磁场的模拟是在Weaver(1965)提出的模型基础上进行的.基于线性叠加理论将同一频率对应的所有传播方向组成波产生的感应电磁场进行叠加,得到不同频率海浪运动产生的感应电磁场(张宝强, 2018).在得到海浪运动感应磁场频谱后,再对其进行逆傅里叶变换可得到相应的时间序列. 假设地磁场为50000 nT,风速为8 m·s-1,海水深度为50 m,采样率为10 Hz,采样时间为1 h.图5显示了模拟得到的海浪感应磁场时间序列和振幅谱(张宝强, 2018).模拟海浪感应磁噪声的能量主要集中在0.08~0.2 Hz频段内,表现为窄带谱特征.在处理过程中,只在上文模拟获得的MT磁场时间序列中加入海浪感应噪声.图6展示了加入海浪感应磁噪声前后的时间序列和时频谱.从图中可以看到,加噪数据时频谱在0.1 Hz附近出现了强能量带. 为了验证K-SVD字典学习方法抑制海浪感应磁噪声的效果,将经过带通滤波处理后的数据作为输入数据,利用本文提出的方法进行去噪处理.K-SVD字典的大小为512×1024,X分量和Y分量数据的噪声增益系数分别选为2.66和2.25,经过10次迭代提取出海浪感应磁噪声.为了对比起见,分别将CEEMDAN和小波阈值去噪方法应用到海浪感应磁噪声压制中.利用CEEMDAN算法可以将输入的含噪声信号分解成有限个具有不同频率成分的固有模态函数(Intrinsic Mode Function, IMF),通过舍弃与海浪感应磁噪声相关的IMF实现压制海浪感应磁噪声的目的(于彩霞等, 2010).在实验中,假定模态平均次数为500.在小波阈值去噪实验中,选用dmey小波作为基函数,采用折衷阈值规则对经过小波分析得到的第5层和第6层细节系数进行阈值处理.最终得到的去噪结果如图7所示.K-SVD字典学习方法能够较为准确地提取出海浪感应磁噪声,重构后的大地电磁磁信号误差也较小. 为了进一步衡量去噪效果,引入三个评价指标,即重构信号信噪比(SNR),均方根误差(RMSE)和归一化互相关系数(NCC): (14) (15) (16) 其中,c(i)和r(i)分别代表无噪信号c和去噪信号r的第i个元素,L代表信号长度.分别计算带噪声 图5 模拟海浪感应磁场X分量(a,b)和Y分量(c,d) (a),(c) 时间序列; (b),(d) 振幅谱.Fig.5 Simulated X component (a,b) and Y component (c,d) of the wave-induced magnetic field (a), (c) Time series; (b), (d) Amplitude spectrum. 图6 模拟海洋大地电磁Hx分量(a,b,c)和Hy分量(d,e,f)加噪前后对比 (a),(d) 加噪前后时间序列; (b),(e) 加噪前时频谱; (c),(f) 加噪后时频谱.Fig.6 Simulated horizontal magnetic Hx component (a,b,c) and Hy component (d,e,f) (a), (d) Time series of clean signal and noisy signal; (b), (e) Spectrogram of clean signal; (c), (f) Spectrogram of noisy signal. 图7 模拟海洋大地电磁Hx分量(a,b,c,d)和Hy分量(e,f,g,h)去噪前后时间序列细节对比Fig.7 Comparison of time series segment before and after denoising of simulated Hx (a,b,c,d) and Hy (e,f,g,h) components 图8 去噪效果评价指标对比 (a) 信号信噪比(SNR); (b) 均方根误差(RMSE); (c) 归一化互相关系数(NCC).Fig.8 Comparison of evaluation indicators (a) Signal noise ratio; (b) Root mean squared error; (c) Normalized cross correlation. 图9 模拟海洋大地电磁数据视电阻率曲线和相位曲线 图中灰线和黑线代表无噪数据Robust阻抗估计结果. (a) 含噪声信号; (b) CEEMDAN方法; (c) 小波阈值去噪方法; (d) K-SVD字典学习方法.Fig.9 Apparent resistivity and phase curves of simulated MT data The gray and black lines in the Figure represent the Robust impedance estimation results of clean data. (a) Noisy signal; (b) CEEMDAN method; (c) Wavelet method; (d) K-SVD dictionary learning method. 图10 南黄海测站1实测海洋大地电磁数据 灰圈部分为由海浪运动感应磁噪声引起的噪声干扰. (a)—(d) 四分量海洋大地电磁数据时间序列; (e,f) 磁场水平分量振幅谱.Fig.10 Measured marine MT data from site 1 deployed in the South Yellow Sea The interference caused by the wave-induced magnetic noise can be seen clearly in the gray circle. (a)—(d) Time series of marine MT data; (e,f) Amplitude spectrum of horizontal component of magnetic field. 图11 实测水平磁场Hx(a,b,c)和Hy(d,e,f)数据去噪效果对比 (a),(d) 去噪前后时间序列; (b),(e) 去噪前时频谱; (c),(f) 去噪后时频谱.Fig.11 Denoised results of measured horizontal magnetic Hx (a,b,c) and Hy (d,e,f) components (a),(d) Time series before and after denoising; (b),(e) Spectrogram of noisy signal; (c),(f) Spectrogram of denoised signal. 信号和经过上述方法去噪后信号的信噪比、均方根误差以及归一化互相关系数,计算结果如图8所示.在经过CEEMDAN和小波阈值去噪方法处理后,MT数据的质量均得到改善.但经过K-SVD字典学习方法去噪后的信号具有更高的信噪比、更小的均方根误差和更大的归一化互相关系数.其中,Hx分量的信噪比由加噪后的-1.3093 dB提高为12.1848 dB,均方根误差由0.5116减小至0.1082,归一化互相关系数由0.6573提高为0.9694.Hy分量的信噪比由加噪后的1.3777 dB提高为12.5642 dB,均方根误差由0.3618减小至0.0998,归一化互相关系数由0.7602提高为0.9720. 对加入强能量噪声后的电磁数据和分别经过CEEMDAN、小波阈值去噪和K-SVD字典学习方法去噪后的电磁数据进行Robust阻抗估计,并计算视电阻率和相位,计算结果如图9所示.在加入海浪感应噪声后,视电阻率和相位在受干扰的4~10 s周期范围内出现较大程度的畸变.CEEMDAN和小波阈值去噪方法可以在一定程度上抑制视电阻率曲线的畸变.但经过K-SVD字典学习方法去噪处理后,视电阻率曲线和相位曲线变得更加光滑和连续.可见在强能量海浪感应噪声干扰下,K-SVD字典学习方法能取得较好的去噪效果. 利用上述方法对南黄海三个测点(测站1、测站2和测站3)的实测海洋大地电磁数据进行处理分析,进一步验证方法的应用效果.测区海域水深为21 m左右.以测站1为例,选择平潮期采样率为500 Hz、时长100 min的实测数据进行去噪处理.选择平潮期数据是为了尽量减少由于潮汐运动所造成的电磁噪声干扰(徐震寰和李予国, 2019).图10显示的是实测电磁场水平分量的时间序列和磁场水平分量的振幅谱.由图10e和图10f可见,磁场水平分量的振幅谱在频率0.1~0.3 Hz内出现噪声干扰,其中Hx分量尤为明显. 利用上文方法对图10所示的南黄海实测数据进行处理分析,其中Hx分量的带通滤波范围为0.1~0.25 Hz,Hy分量的带通滤波范围为0.1~0.2 Hz,字典D的大小选为1024×2048.由于实测数据的采样率为500 Hz,而所要提取的海浪感应磁噪声的主频在10 s附近.此时字典中原子(列向量)的长度甚至不能覆盖一个海浪感应磁信号的周期.为了从训练集中寻找到与海浪感应磁噪声特征相符合的原子,有必要对实测数据进行降采样处理. 将经过10 Hz降采样处理后的数据作为训练集,在提取到海浪感应磁噪声信号后,对其再以500 Hz进行升采样处理.将升采样数据从原始的磁场时间序列中减去,便可得到去噪后数据,去噪结果如图11所示.由图11c可见,去噪后的Hx分量中由海浪感应磁场引起的强能量得到压制,恢复到正常的数量级.提取出的海浪感应磁噪声如图12所示,其时间序列与模拟的海浪感应磁噪声相似,均具有窄带谱的特征.而Hy分量由于受到海浪感应磁场的影响较小,去噪前后的时频谱差异不大. 此外,我们也选取了1号站位Hx分量部分数据与南海实测大地电磁磁场数据进行了对比,结果见图13.南海大地电磁数据采集于深水区,水深约767 m.与浅水环境相比,深水区所获取的大地电磁数据受海浪运动影响较小,在0.1~0.3 Hz频率范围内没有出现明显的噪声干扰,数据质量较高.在经过去噪后,南黄海实测数据时间序列中由海浪感应磁噪声所造成的规律性正弦型干扰得到压制. 图12 提取的海浪感应磁噪声 (a) 时间序列; (b) 振幅谱.Fig.12 The wave-induced magnetic noise extracted by the K-SVD method (a) Time series; (b) Amplitude spectrum. 同样地,利用Robust阻抗估计方法对去噪前后的实测数据进行阻抗估计并计算视电阻率和相位.由于相对较高频部分(>0.1 Hz)存在随机噪声干扰,在处理中选择小时窗进行阻抗估计,从而可以获得较多窗口叠加.而低频部分则选择大时窗进行阻抗估计.最后将这两部分数据进行拼接处理,得到最终的视电阻率曲线和相位曲线,如图14所示.图14a展示的是去噪前的结果,可见在海浪感应磁场的影响下,TE模式和TM模式的视电阻率曲线、相位曲线在周期3~10 s之间均出现了畸变.而其他时段因为受到的海浪感应噪声干扰较小,视电阻率曲线和相位曲线相对比较光滑.经过K-SVD算法去噪后的结果见图14b,视电阻率曲线得到明显改善,在周期3~10 s之间变得比较光滑.虽然相位曲线相较于原始数据的结果也有了改善,但是在周期4~5 s之间有一个频点的结果不理想.利用式(10)对其校正,结果见图14c.经过相位校正后,相位曲线变得更加连续. 利用相同的方法,对南黄海测站2和测站3的实测大地电磁数据进行了去噪处理,经Robust阻抗估计后得到的视电阻率和相位曲线如图15所示.实测数据的处理结果表明,K-SVD字典学习方法可以有效地压制海浪感应磁噪声干扰,提高MT数据的质量.同时能够基于校正后的视电阻率信息实现相位校正,最终得到的视电阻率与相位曲线更加连续、光滑. 浅水区的大地电磁勘探极易受到海浪感应电磁场的影响,海浪对磁场的影响主要集中在1~30 s的周期范围内,呈现出贯穿全时段的强能量干扰.为压制海浪感应磁噪声,本文将K-SVD字典学习方法与相位校正方法应用于海洋MT数据处理中.通过仿真测试以及南黄海实测数据的处理分析,结果表明该方法能够有效压制海浪感应磁噪声,提高MT观测数据的质量,并改善视电阻率及相位曲线. 图13 南黄海(水深21 m)与南海(水深767 m)实测 大地电磁数据对比 (a) 时间序列; (b) 南黄海测站1部分数据去噪前后的 振幅谱; (c) 南海数据的振幅谱.Fig.13 Comparison of marine MT data from the South Yellow Sea (21 m) and the South China Sea (767 m) (a) Time series; (b) Amplitude spectrum of data from South Yellow Sea; (c) Amplitude spectrum of data from South China Sea. 本文提出的方法适用于提取时间序列中规律性信号.在实际的去噪工作中,通常需要经过多次试验确定最优噪声增益系数.如何高效、准确地寻找最优增益系数是需要进一步研究的工作. 致谢感谢三位匿名审稿专家给出的宝贵的意见和建议.本文的研究工作受到国家自然科学基金项目的资助,在此表示诚挚的感谢. 图14 测站1实测数据视电阻率和相位曲线 (a) Robust估计; (b) 经K-SVD方法去噪后; (c) 经相位校正后.Fig.14 Apparent resistivity and phase curves of measured data from site 1 (a) Robust estimation; (b) K-SVD method; (c) Phase correction.



1.2 基于视电阻率信息的相位校正方法
1.3 海浪感应磁噪声压制与相位校正流程

2 模拟数据噪声抑制
2.1 模拟海洋MT信号时间序列




2.2 模拟海浪感应磁场时间序列





3 实测数据噪声抑制
4 结语


