基于瞬时相位的微地震干涉定位方法研究

战婷婷， 李磊， 陈浩

1 中国科学院声学研究所声场声信息国家重点实验室， 北京 100190 2 中国科学院大学， 北京 100049 3 北京市海洋深部钻探测量工程技术研究中心， 北京 100190 4 中南大学地球科学与信息物理学院， 长沙 410083 5 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学)， 长沙 410083

0 引言

微地震监测技术是利用地下应力场变化导致岩层破裂而诱发的微弱地震波进行储层监测和描述的地球物理方法(Maxwell, 2014; Li et al., 2019; 李政等，2019).该方法是根据震源位置的分布对裂缝形态或储层流体运动进行监测，因此震源定位是微地震数据处理和解释的基础.研究者们借鉴反射地震勘探中偏移叠加的思想，提出了一些无需初至拾取、利用多道波形信息的自动震源定位方法(Kao and Shan, 2004; 许力生等，2013；李振春等，2014；Cesca and Grigoli, 2015; Li et al., 2020).这类方法中研究最成熟且应用最广的是波形叠加法.波形叠加法的核心思想是采用不同的偏移核函数进行波束形成，即挖掘走时和幅度之间的对应关系对地震震源能量进行聚焦和成像，从而实现震源定位(Gajewski et al., 2007; 王维波等，2012；曹雷，2015；Li et al., 2018).

地震干涉成像是一种具有代表性的偏移叠加类震源定位法.该方法基于震源到不同检波器的走时差，消除了震源激发时刻对定位精度的影响.由于采用走时差信息提取对应的互相关波形进行叠加，该方法也被称作互相关叠加或互相关偏移(Li et al., 2018).Schuster等(2004)首次提出地震干涉法可以对被动地震数据进行震源定位.Li等(2015)提出了加权弹性波干涉成像，该方法通过考虑不同震相的加权组合，提高了定位结果的可靠性.Poiata等(2016)提出基于多频段的互相关叠加震源定位法，并将其成功应用于智利中部地区的地震检测和定位.Wu等(2018)通过将反褶积干涉与互相关偏移结合，提出了微地震定位的反褶积偏移方法，合成算例和实际算例均表明新方法能大幅提高成像分辨率，并降低了对速度模型误差的敏感性.田宵等(2020)在加权弹性波干涉成像的基础上提出了增加同一检波器的S-P波走时差信息的全干涉成像方法，能够显著降低震源-检波器方向的定位误差和伪像.由于微地震事件一般具有复杂的震源机制，为了消除震源辐射花样导致的初至极性变化的影响，避免出现波形相消叠加的问题，一般需要采用特征函数对原始波形进行转换.目前主要的特征函数有绝对值(Kao and Shan, 2004)、波形包络(Gharti et al., 2010)、振幅的平方(Gajewski et al., 2007)和长短时窗能量比(Short Time Average to Long Time Average ratio, STA/LTA)(Grigoli et al., 2013)等.Trojanowski和Eisner(2016)从数值和理论分析两方面表明，绝对值等特征函数会降低波形叠加的噪声压制性能，对波形极性简单的校正就能显著提高事件检测和定位效果，而与波形相似性/互相关叠加定位方法相结合可以获得更好的定位结果.Beskardes等(2018)对比了基于原始波形、波形包络、长短时窗能量比(STA/LTA)和峰度(Kurtosis)四种特征函数的微地震定位方法，结果表明：一方面原始波形能够提供最佳的空间分辨率，保留幅度信息并增强了检测微弱事件的能力，但对速度误差、极性误差和突发噪声最为敏感；另一方面其他特征函数能有效避免初至极性的影响并降低对速度误差的敏感性，但牺牲了成像的空间分辨率并且容易受噪声影响.震源定位和震源机制联合反演法是一种消除初至极性变化影响的替代方案，但是这种方法反演速度较慢，对数据质量要求较高，并且还可能会将震源机制反演过程中的误差引入定位结果中(Staněk et al., 2015).

除了幅度信息，相位信息也能体现波形极性.Schimmel和Paulssen(1997)提出了一种基于瞬时相位相干度量的相位加权叠加法(Phase-Weighted Stack, PWS).王晓欣等(2017)将PWS方法用于天然地震事件的定位中，通过理论地震图计算验证了方法的可靠性.Tan(2019)详细验证了PWS相对于其他方法的优越性，发现PWS具有更好的空间分辨率，提高了微弱地震事件的可检测性.

本文从原始互相关波形出发，将包含波形极性信息的相位属性引入干涉成像法中，通过重新组合原始互相关波形的振幅和瞬时相位信息，提出了一种同时基于振幅和瞬时相位信息的干涉成像方法——互相关相位加权成像法(Cross-Correlation Phase-Weighted imaging method, CCPW)，实现校正波形极性以及提高抗噪性和成像分辨率的目的.然后，与基于绝对值干涉成像法(Absolute value-based Interferometric Imaging method, AII)和基于STA/LTA干涉成像法(STA/LTA-based Interferometric Imaging method, SLII)一起，采用地面监测的水平分层理论模型分析了随机噪声、分辨率、速度模型误差和震相数量等因素对定位结果的影响.最后将三种方法应用到矿震地面监测的现场数据中，结果表明，提出的定位方法具有较强的抗噪性并提高了成像分辨率，但定位结果受高幅值S波等的相干干扰，并且对速度模型的误差敏感.

1 基本原理

1.1 微地震干涉成像

微地震干涉成像的基本原理：建立速度模型并离散化，通过射线追踪或求解程函方程计算得到检波器到速度模型中各离散点的直达波走时表，提取震源到独立检波器对的走时差并对相应的互相关波形进行偏移叠加，叠加所有检波器对的成像结果生成最终震源成像剖面(Schuster et al., 2004; Li et al., 2015).对应的干涉成像方程如下：

(1)

(2)

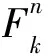
1.2 互相关相位加权成像法

对地震信号s(t)做希尔伯特变换H[s(t)]，并构建解析信号sa(t)如下：

sa(t)=s(t)+iH[s(t)]=A(t)exp[iφ(t)],

(3)

(4)

式中，A(t)和φ(t)为随时间变化的包络和瞬时相位.

对逐采样点归一化的解析信号exp[iφ(t)]进行叠加并归一化，可以得到相位叠加(Phase Stack, PS)w(t)：

(5)

(6)

式中，φl(t)为第l道的瞬时相位，v为控制最终相位叠加曲线w(t)尖锐程度的指数，也能够控制随机噪声经过叠加后的衰减程度.式(6)表明只有相位一致的有效信号才能得到相干叠加，其他相位随机变化的噪声信号经过叠加只能得到一个小值(Schimmel and Paulssen, 1997).

为了抑制不相干的叠加信号，将相位叠加作为线性叠加的时间相关的权重，得到相位加权叠加(PWS)gPWS(t)：

(7)

而微地震事件具有复杂的震源机制，将式(7)直接用于微地震事件的定位时(王晓欣等，2017；Tan, 2019)，未考虑具有不同极性的波形对定位结果的影响.于是，为了校正波形极性对定位结果的影响，考虑重新组合振幅和瞬时相位属性信息，并应用于干涉成像方法中.

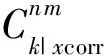
(8)

从表1的推导可以发现，无论波形的振幅极性为正或为负，通过新方法的处理，最后加权乘积的结果均变换为波形的振幅极性为正时的乘积形式，也就是说波形的极性得到了校正.

表1 互相关相位加权成像法极性校正原理Table 1 Polarity correlation principle of CCPW

(9)

2 数值模拟

2.1 均匀模型下的方法验证

首先，通过简单的二维均匀介质模型验证方法的有效性，采用地面阵列监测，震源为加载在正应力分量上的爆炸震源，震源函数为雷克子波函数，其他相应参数见表2.

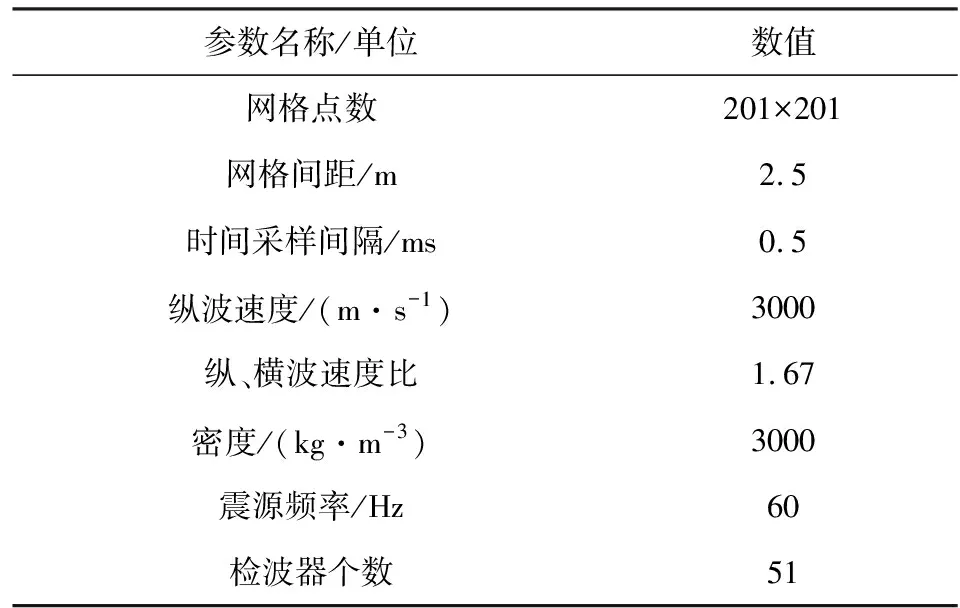
表2 二维均匀模型参数Table 2 Parameters of two-dimensional homogeneous model

地面51道检波器接收到的波形如图1所示.由图可见，在均匀速度模型中爆炸源只激发P波，Vx分量接收到的波形关于震源位置的横坐标有明显的初至极性变化，而Vz分量接收到的波形极性一致.

图1 合成微地震记录 (a) Vx分量; (b) Vz分量.Fig.1 Synthetic microseismic records (a) Vx component; (b) Vz component.

以Vx分量的第1道与第13道的原始互相关波形和第1道与第38道的原始互相关波形为例，说明互相关相位加权成像法是如何校正波形极性的.图2(a,b)分别为上述两道波形极性相反的原始互相关波形，图2(c,d)分别为由式(5)得到的这两道原始互相关波形对应的逐采样点归一化的解析信号，图2(e,f)分别为由式(8)得到的两道原始互相关波形与其对应的逐采样点归一化的解析信号的加权乘积，其中六角星代表参考点，图2c中已示出各象限位置，且图2(d—f)中的象限位置与其一致，图中水平和垂直的黑色实线分别表示实轴和虚轴的位置.在由实轴为横轴和虚轴为纵轴构成的复数平面中，逐采样点归一化的解析信号中点的实部的极性决定该点落在虚轴右侧还是左侧，即当实部极性为正时，该点落在虚轴的右侧，也就是第一和第四象限，反之当实部极性为负时，该点落在虚轴左侧也就是第二和第三象限.由式(3)中解析信号的实部为原始互相关波形可知，此时式(5)中经过逐采样点归一化的解析信号中只包含相位信息且点的实部的极性与原始互相关波形中点的极性一致，也就是说由于图2c、d中两个逐采样点归一化解析信号中的点在虚轴左右两侧均存在，且两个原始互相关波形中对应颜色的参考点此时恰好分布在大约关于原点对称的位置上，表明两个原始互相关波形的极性相反，而图2e、f中加权乘积后信号中对应颜色的参考点则分别以近似相同的相位落在了虚轴右侧的第一和第四象限中距离原点与振幅大小相等的位置上，说明经过变换后的波形极性得到了校正.

图2 互相关相位加权成像法的极性校正原理示意图 (a,b) 第1道分别与第13道、第38道的原始互相关波形； (c,d) 原始互相关波形(a)和(b)对应的逐采样点归一化的解析信号； (e,f) 原始互相关波形与对应的逐采样点归一化的解析信号的加权乘积.Fig.2 Sketch of polarity correction principle of CCPW (a,b) The original cross-correlation waveforms of the 1st trace and the 13th trace, the 38th trace, respectively; (c,d) The analytical signals normalized sample by sample corresponding to the original cross-correlation waveforms (a) and (b); (e,f) The weighted products of the original cross-correlation waveforms and the corresponding analytical signals normalized sample by sample.

v的作用可由图3说明，从式(9)可知，v是针对归一化后的叠加值操作的，此时的叠加值大小在[0,1]范围内.从图3中不同v的取值对应的叠加值变化曲线可以看出：将叠加值取指数v后，不同叠加值的衰减程度不同，相同v的取值下，由随机噪声引起的低叠加值衰减程度明显大于由有效信号引起的高叠加值，凸显了震源能量，最终的成像分辨率得到提高；同时，当v的取值在[2,5]内时，对低叠加值的衰减效果已经十分有效，且随着指数v的取值越大，越抑制高叠加值，对低叠加值的衰减效果则变化不大.故本文的v值在该范围内选取，以防止过高的v的取值导致定位结果出现不稳定性问题.

现在，Vx分量的独立且不重复的原始互相关波形经过线性偏移叠加和经过互相关相位加权成像法偏移叠加后的波形对比如图4a所示，可以发现：有正负极性变化的原始互相关波形经过线性偏移叠加后相互抵消，无法得到有效的能量峰值；而经过互相关相位加权成像法得到的叠加波形中存在有效的高能量峰值，说明原始互相关波形的极性得到了校正；通过控制v的取值可以削弱旁瓣，并且随着v的取值增大，叠加波形的旁瓣被衰减的越明显.

图3 最终叠加值随指数v的取值变化示意图Fig.3 Sketch of the final stacked value changing with the value of exponent v

为了说明互相关相位加权成像法与基于绝对值干涉成像法的区别，向Vx分量的每道原始波形中分别添加了所有道波形最高振幅的均方差40%的高斯随机噪声，独立且不重复的原始互相关波形经过二者处理后得到的叠加波形如图4b所示：当v=1时，互相关相位加权成像法和基于绝对值干涉成像法的叠加结果类似；由于互相关相位加权成像法中引入了相位信息，瞬时相位随机变化的噪声信号在叠加过程中得到了有效的衰减，提高了方法的抗噪性；与压制旁瓣一样，随机噪声也可以通过调整v的取值进一步削弱，提高最终成像分辨率.也就是说，由于互相关相位加权成像法的叠加结果受振幅和瞬时相位共同影响，相比在时域中简单叠加波形幅度的基于绝对值干涉成像法具有更好的抗噪性和成像分辨率.

图4 互相关波形偏移叠加结果对比 (a) 无噪Vx分量，所有独立的原始互相关波形经过线性偏移叠加和互相关相位加权成像法偏移叠加得到的波形(v的取值分别为1，2，4)； (b) 含噪Vx分量，所有独立的原始互相关波形经过取绝对值后线性偏移叠加和互相关相位加权成像法偏移叠加得到 的波形(v的取值分别为1，2，4).Fig.4 Comparison of cross-correlation waveforms migration stacking results (a) Vx component without noise, the waveforms obtained by linear migration stacking and CCPW migration stacking (the values of v are 1, 2, 4, respectively) of all independent and original cross-correlation waveforms; (b) Vx component with noise, the waveforms obtained by linear migration stacking after taking absolute value and CCPW migration stacking (the values of v are 1, 2, 4, respectively) of all independent and original cross-correlation waveforms.

基于原始波形干涉成像法、互相关相位加权成像法、基于绝对值干涉成像法和基于STA/LTA干涉成像法对无噪Vx分量成像结果的对比如图5所示，能够发现互相关相位加权成像法不仅校正了波形极性变化对定位结果的影响，还明显地提高了最终的成像分辨率.

2.2 分层模型下的方法性能对比测试

为了进一步验证互相关相位加权成像法的稳定性和可靠性，基于二维水平分层各向同性介质模型进行了系列数值试验.速度模型及震源-检波器阵列示意图如图6a所示，图中三层水平分层模型参数如下：由上到下的层密度依次为2000 kg·m-3、2500 kg·m-3和3000 kg·m-3，层纵波速度依次为2000 m·s-1、2500 m·s-1和3000 m·s-1，纵横波速度比均为1.67.为不失一般性，在不同位置设置四个震源S1、S2、S3和S4，相应的位置信息已在图中示出，并独立激发分别对应研究了随机噪声、分辨率、速度模型误差和震相数量等因素对各种方法定位结果的影响.其中，互相关相位加权成像法中v的取值为2， STA/LTA方法中短时窗的长度为7.5 ms，长时窗长度为15 ms.所有震源均是水平激发的集中力源，其他参数与上述均匀介质模型参数一致.图6b、c分别为向震源S1的每道原始波形中添加所有道波形最高振幅的均方差50%的高斯随机噪声后的Vx分量和Vz分量.

2.2.1 随机噪声

首先向震源S1的各道原始波形中分别添加所有道波形最高振幅的均方差20%、30%、40%和50%的高斯随机噪声，并采用蒙特卡洛方法研究定位的不确定性(Maxwell, 2009; Tian et al., 2016,2017)，其主要做法是对每种噪声水平，预先生成100组随机噪声并添加在原始波形上，进行100次定位，最后根据100次定位结果分析其分布特征和稳定性(鲁棒性).三种方法在各噪声水平下100次蒙特卡洛模拟的定位结果如图7所示，结果表明：所有方法的定位误差主要集中在垂直方向(Z)，这是由于干涉成像法的二维成像剖面是由双曲状条纹叠加构成的，导致在地面监测条件下对垂直方向(Z)的约束较差，但在复杂速度模型下水平方向也会出现较大定位误差；抗噪性效果最好的是互相关相位加权成像法，其次是基于绝对值干涉成像法，最差的是基于STA/LTA干涉成像法；尤其当信噪比较低时(40%～50%)，新方法包含相位信息的偏移叠加方式相比基于绝对值干涉成像法的偏移叠加方式的优势逐渐体现出来，较大程度上降低了随机噪声对定位结果的影响；而STA/LTA方法的震相识别精度受随机噪声影响大，进而影响了最终定位结果的准确性.

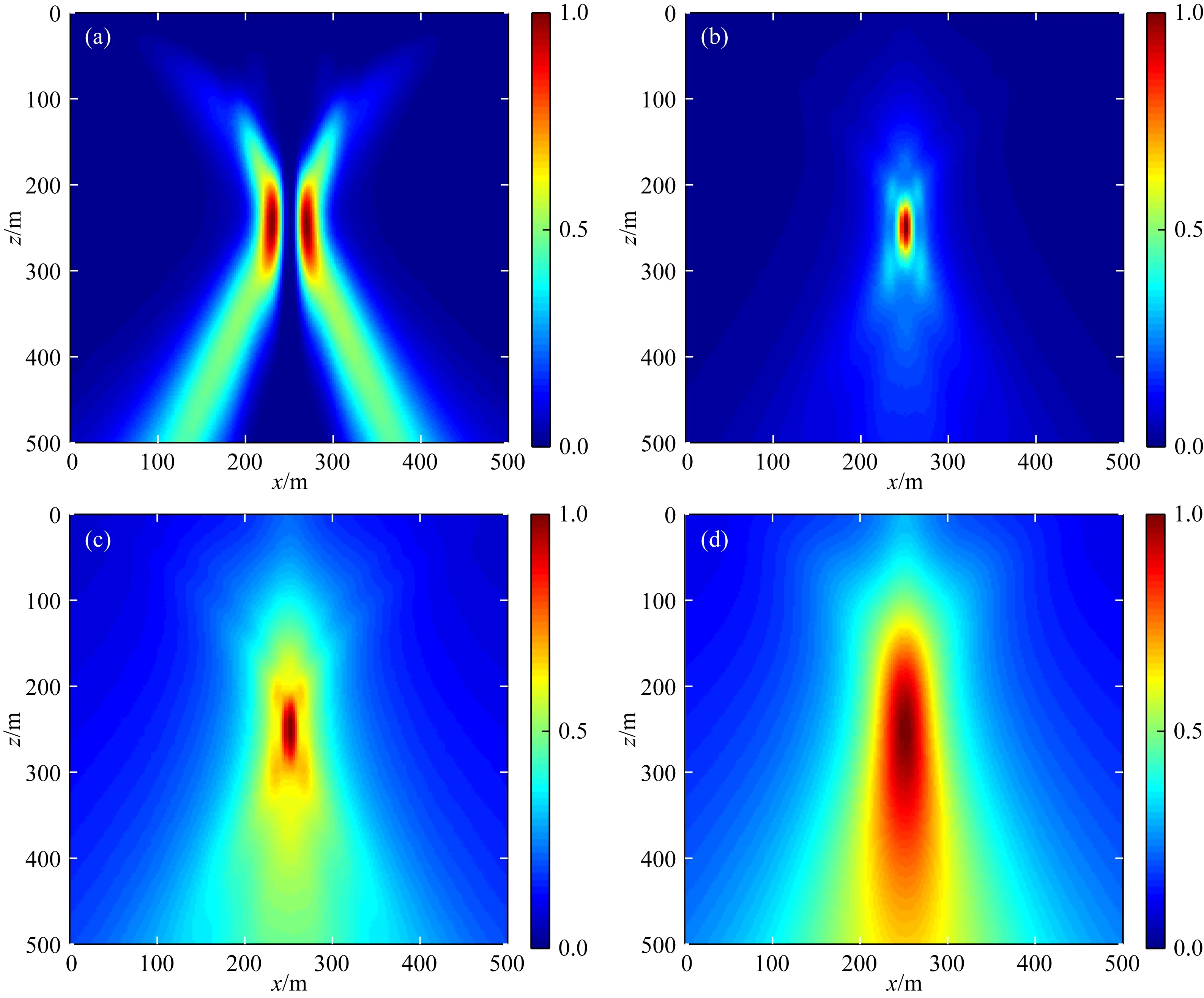
图5 无噪声Vx分量的干涉成像结果 (a) 基于原始波形干涉成像法； (b) 互相关相位加权成像法(v=2)； (c) 基于绝对值干涉成像法； (d) 基于长短时窗能量比干涉成像法.Fig.5 Interferometric imaging results of the Vx component without noise (a) The original waveform-based interferometric imaging; (b) CCPW (v=2); (c) AII; (d) SLII.

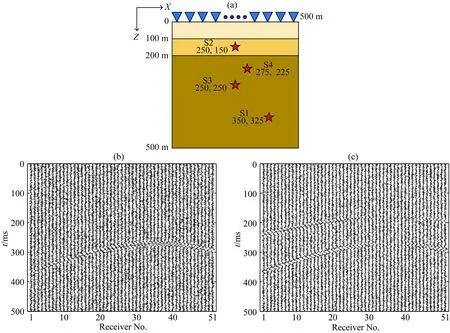
图6 (a)速度模型和震源-检波器阵列示意图；震源S1添加噪声后的(b)Vx分量波形和(c)Vz分量波形Fig.6 (a) Sketch of velocity model and source-receiver array; (b) Vx component waveforms and (c) Vz component waveforms of S1 with noise

2.2.2 分辨率

向震源S2的各道原始波形中添加了所有道波形最高振幅的均方差30%的高斯随机噪声，测试三种方法在低信噪比条件下的成像分辨率.已知波形的绝对频宽影响分辨率，频宽越大，波形“越瘦”，分辨率越高.根据该特性来确定震源成像的空间分辨率：利用成像剖面中过震源位置的归一化成像值曲线的最高幅值的0.707倍对应的横坐标宽度表示成像分辨率，此时横坐标宽度“越小”代表成像值曲线“越瘦”，成像分辨率越高.通过这种量化的成像分辨率定义方式能够直观的比较各震源成像结果的分辨率大小.三种方法的成像剖面中过震源位置的水平方向(X)和垂直方向(Z)的成像值曲线对比如图8所示，幅值0.707对应图中黑色点线，可以看出：无论是水平方向(X)还是垂直方向(Z)，由黑色点线截取的成像值曲线宽度由小到大依次为：互相关相位加权成像法、基于绝对值干涉成像法和基于STA/LTA干涉成像法，即对应着成像分辨率逐渐降低.该测试结果进一步说明了STA/LTA方法受随机噪声影响大，当波形中随机噪声含量增大时，震相识别后的波形分辨率降低，进而导致最终成像分辨率变差.互相关相位加权成像法则通过包含瞬时相位信息的多道波形偏移叠加和指数v的适当取值显著地提高了最终成像分辨率.

2.2.3 速度模型误差

在实际微地震定位过程中，速度模型总会存在一定的误差，导致定位结果的不准确.为考察三种方法对速度模型的依赖性，在各层的P、S波速度模型中分别添加±20%、±15%和±10%的速度误差，共得到六种速度模型.以震源S3产生的理论波形为例，为了排除其他因素干扰，此时原始波形中不添加随机噪声.三种方法在六种速度模型下的定位结果与正确震源位置之间的绝对误差如表3所示，定位结果对比如图9所示.当速度模型存在误差时，所有方法的定位结果均相对正确震源位置发生了偏移，且这种偏移只发生在垂直方向(Z)上.这是因为检波器阵列布设于地面且关于震源位置的横坐标对称分布，震源水平方向(X)的定位误差由于走时误差的对称约束而抵消了，而在复杂模型中，特别是存在横向速度变化的时候水平方向也会出现定位误差.当速度模型值减小时，定位结果越远离检波器阵列，且此时的定位误差要大于速度模型值增大时的定位误差.因为当速度值减小时，模型中各离散点到检波器对的理论计算走时差增大，只有更加远离检波器阵列的离散点能吻合实际的互相关波形.相反，当速度模型值增大时，震源被定位到更加靠近检波器阵列的错误位置.此外，添加速度误差的绝对值相同的条件下，速度模型减小(-20%)比速度模型增大(+20%)造成的走时差误差更大，导致了速度值减小时的定位误差更大.分辨率较高的互相关相位加权成像法和基于绝对值干涉成像法的定位误差整体上要大于分辨率较低的基于STA/LTA干涉成像法的定位误差.这是因为波形分辨率越高，对速度模型的误差越敏感，定位结果的误差也越大.

图7 不同噪声条件下的100次蒙特卡洛模拟的定位结果 (a) 互相关相位加权成像法； (b) 基于绝对值干涉成像法； (c) 基于长短时窗能量比干涉成像法.Fig.7 Location results of Monte Carlo simulation by 100 times under different noise conditions (a) CCPW; (b) AII; (c) SLII.

图8 三种方法的成像剖面中过震源位置的归一化成像值曲线对比 (a) 水平方向(X)； (b) 垂直方向(Z).Fig.8 Comparison of normalized imaging value curves passing through the source location in imaging profiles of three methods (a) Horizontal direction (X); (b) Vertical direction (Z).

图9 三种方法在六种速度模型下的定位结果对比(品红色五角星为正确震源位置) (a) 互相关相位加权成像法； (b) 基于绝对值干涉成像法； (c) 基于长短时窗能量比干涉成像法.Fig.9 Comparison of location results of three methods under six velocity models (The magenta pentagram represents the correct source location) (a) CCPW; (b) AII; (c) SLII.

图10 三种方法利用不同震相组合的成像结果 (a,c,e) 只利用Vz分量中P波的成像结果; (b,d,f) 同时利用Vx分量的S波和Vz分量的P波的成像结果. (a,b) 互相关相位加权成像法； (c,d) 基于绝对值干涉成像法； (e,f) 基于长短时窗能量比干涉成像法.Fig.10 Imaging results of three methods using different seismic phase combinations (a,c,e) The imaging results using only the P wave in the Vz component; (b,d,f) The imaging results using the S wave in the Vx component and the P wave in the Vz component at the same time. (a,b) CCPW; (c,d) AII; (e,f) SLII.

图11 三种方法对100个强微地震事件在(a)E-N平面和(b)E-Z平面内的定位结果和 100个弱微地震事件在(c)E-N平面和(d)E-Z平面内的定位结果 其中，红色圆点代表走时反演得到的震源位置，绿色、青色和蓝色圆圈分别代表互相关相位加权成像法、 基于绝对值干涉成像法和基于长短时窗能量比干涉成像法的定位结果，紫色菱形代表检波器.Fig.11 Location results of 100 strong microseismic events in (a) E-N plane and (b) E-Z plane and 100 weak microseismic events in (c) E-N plane and (d) E-Z plane obtained by three methods The red dots represent the source locations obtained by travel time inversion, the green, cyan, and blue circles represent the location results of CCPW, AII, and SLII, respectively, and the purple diamonds represent the receivers.

图12 三种方法对序号为10的弱微地震事件的成像结果(白色五角星为走时反演定位结果) (a，b) 互相关相位加权成像法； (c，d) 基于绝对值干涉成像法； (e，f) 基于长短时窗能量比干涉成像法.Fig.12 Imaging results of No.10 weak microseismic event obtained by three methods (The white pentagram represents the source location obtained by travel time inversion) (a，b) CCPW; (c，d) AII; (e，f) SLII.

图13 (a) 序号为90的强微地震事件的Vz分量波形图；互相关相位加权成像法分别对红色实线框和 红色虚线框内波形得到的关于P波成像的垂直剖面图(b)和(c)(白色五角星为走时反演定位结果).Fig.13 (a) Waveforms of Vz component of the No. 90 strong microseismic event; (b) and (c) Vertical imaging profiles for P-waves in the red solid line border and red dashed line border obtained by CCPW (The white pentagram represents the source location obtained by travel time inversion).

图14 序号为90的强微地震事件的(a)Vx分量； (b) 经STA/LTA处理后的水平分量； (c) Vz分量； (d) 经STA/LTA处理后的Vz分量Fig.14 (a) Vx component； (b) horizontal component processed by STA/LTA； (c) Vz component ； (d) Vz component processed by STA/LTA of the No.90 strong microseismic event

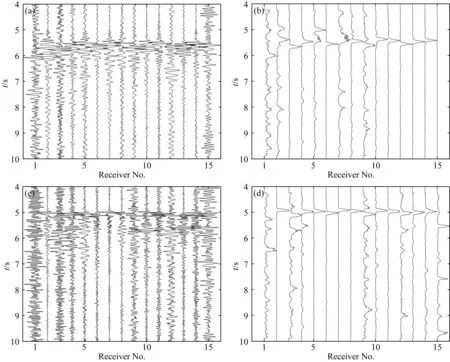
图15 序号为10的弱微地震事件的(a) Vx分量； (b) 经STA/LTA处理后的水平分量； (c) Vz分量； (d) 经STA/LTA处理后的Vz分量Fig.15 (a) Vx component； (b) horizontal component processed by STA/LTA； (c) Vz component and (d) Vz component processed by STA/LTA of the No.10 weak microseismic event

表3 六种速度模型下三种方法定位结果的绝对误差对比 (单位：m)Table 3 Absolute error comparison of location results of three methods under six-velocity models (Unit: m)

2.2.4 震相数量

向震源S4的各道原始波形中添加了所有道波形最高振幅的均方差20%的高斯随机噪声，测试震相数量对三种方法定位结果的影响.图10中三种方法的成像结果表明：同时利用Vz分量中P波和Vx分量中S波的定位结果(图10b,d,f)的伪像压制效果要好于仅利用Vz分量中P波的定位结果(图10a,c,e).各分量的互相关波形中包含的震相对信息有[P-S，P-P，S-S，S-P]，在利用P波走时差对互相关波形中P-P波振幅进行偏移叠加定位时，会将S-S波等其他强相干波的振幅偏移在其他未知的位置上，形成相干伪像.而STA/LTA方法进行了P波和S波震相识别，此时P波的能量得到加强，在一定程度上可能会削弱同分量中S波的相干干扰.

在加权弹性波干涉成像方法中，可以根据实际各震相的强弱选取不同加权系数进行成像，平衡互相关波形中多震相信息的约束和干扰(Li et al., 2015, 2018; 田宵等，2020).本文仅同时利用Vx分量中S波和Vz分量中P波成像，也就是Vx分量和Vz分量中的震相组合[P-S，P-P，S-S，S-P]的权值分别取为[0 0 1 0]和[0 1 0 0].

基于上述数值算例的处理结果，可将本文研究的各种方法的性能总结如表4.

表4 三种方法性能总结Table 4 Summary of the performance of three methods

3 矿震地面监测实际数据

本部分将利用矿震监测数据考察本文提出方法的应用效果，并将定位结果与走时反演定位结果、基于绝对值干涉成像法和基于STA/LTA干涉成像法的定位结果作对比.

矿震监测台网HAMNET是2006—2007年间布设于德国鲁尔地区某煤矿的短期监测平台，包括15个三分量地面地震监测台站.纵波速度为3880 m·s-1，横波速度为2180 m·s-1(Grigoli et al., 2013)，速度模型建立的网格点数为101×101×101，网格间距为50 m，时间采样间隔为5 ms.在监测台网HAMNET实际监测到的多个诱发地震事件中，选取了100个强事件(震级ML>0.5)和100个弱事件(震级ML=-0.8)(Li et al., 2018).基于均匀速度模型，所选取的200个微地震事件基于手动初至拾取的走时反演定位结果如图11中红色圆点所示.为确保波形叠加类定位结果与走时反演结果的可比性，波形叠加类方法对这200个事件定位时仍基于上述均匀速度模型.互相关相位加权成像法中的指数v取为4，STA/LTA的长、短时窗分别取250 ms和125 ms.为了提高定位效率，所有事件的波形经过震相识别后均截取包含微地震事件的6 s波形进行定位.

100个强微地震事件和100个弱微地震事件的定位结果对比如图11所示，弱微地震事件在定位前经过了5～30 Hz的带通滤波处理.其中，三种方法对序号为10 的弱微地震事件的成像结果如图12所示，三种方法均能够较好的定位出该事件的位置，而互相关相位加权成像法具有较高的成像分辨率，伪像得到了很好的压制.

从以上200个现场矿震事件的定位结果看，尤其是强事件的定位结果，从原始波形幅度信息出发进行定位的基于绝对值干涉成像法和互相关相位加权成像法的定位结果，相比于走时反演法和基于STA/LTA干涉成像法的定位结果在垂直剖面上有很大的分散性，分析其可能存在的原因是：

(1)Vz分量中高幅值S波等续至相干波干扰.正如数值模拟分析的一样，在利用基于绝对值干涉成像法和互相关相位加权成像法进行定位时，Vz分量中较强的续至S波和反射波等，会在最终成像结果中引入相干干扰.序号90的强事件为互相关相位加权成像法定位偏差较大的事件之一，其Vz分量如图13a所示.以互相关相位加权成像法利用该事件Vz分量得到的关于P波干涉成像剖面为例，即对图13a中红色实线矩形框内的波形进行关于P波的干涉成像，结果如图13b所示，由于续至在P波之后的高幅值S波和反射波等震相的相干干扰，震源被定位在了错误的位置上.但当将S波截掉，只保留P波震相定位时，即对图13a中红色虚线矩形框内的波形进行关于P波的干涉成像，结果如图13c所示，震源位置与走时反演结果非常接近.而当利用STA/LTA进行定位时，如图14d中序号为90的强事件经过STA/LTA处理后的Vz分量和图15d中序号为10的弱事件经过STA/LTA处理后Vz分量所示，经过震相识别后的Vz分量中P波能量得到了强化，且由于此时P波和S波相距较近，最早到达的P波降低了STA/LTA对后续S波识别的敏感度，这不仅削弱了Vz分量中S波对定位结果的影响，同时还使得对Vx和Vy分量中S波能量的识别产生了一定干扰，有些道甚至无法识别，如图14b和图15b所示，并且这种影响随着P波和S波之间的距离越近而越大.同时，某些随机噪声和高频脉冲也会导致STA/LTA对非微地震信号的误判，如图15(b，d)所示.

(2)用于定位的S波速度模型不准确.通过理论分析能够知道基于绝对值干涉成像法和互相关相位加权成像法的分辨率较高，导致对速度模型误差的敏感度比基于STA/LTA干涉成像法更高，这可能给这两种定位方法的最终结果带来较大的偏差.

4 结论

本文提出了一种基于原始互相关波形的振幅和瞬时相位的微地震干涉成像方法——互相关相位加权成像法，并结合数值算例和现场数据深入对比分析了互相关相位加权成像法、基于绝对值干涉成像法和基于STA/LTA干涉成像方法.

互相关相位加权成像法通过重新组合原始互相关波形的振幅与瞬时相位信息校正了波形极性变化，无需特征函数处理，相比基于绝对值干涉成像法和基于STA/LTA干涉成像法，具有更高的成像分辨率和抗噪性.同时由于分辨率的提高，也导致了新方法对速度模型误差敏感.研究还表明新方法与其他基于波形振幅信息定位的方法一样，定位结果容易受波形中较强的续至波等相干波的影响，本文中当利用弱震相P波定位时，同分量中续至的强震相S波等相干波会导致定位结果出现偏差.

致谢感谢三位匿名审稿专家提供的宝贵审稿意见和期刊编辑的修改.感谢HAMNET项目组公开实际矿震数据(https:∥www.fdsn.org/networks/detail/Z2_2006/).