我国东部地区非随机持续性微震背景噪声场源的特性及定位研究

王俊, 郑秀芬, 刘红桂, 杨大克, 郑定昌,郑江蓉, 詹小艳, 孙业君, 杜航,4

1 江苏省地震局， 南京 210014 2 中国地震局地球物理研究所， 北京 100081 3 云南省地震局， 昆明 650224 4 中国科学技术大学， 合肥 230026

0 引言

近年来，随着地球背景噪声在理论方法及应用研究领域不断取得新的进展，越来越多的科学家将噪声地震学视为一个独立、前沿的重要探索领域，其中背景噪声的特性及其场源分布是核心问题之一.地震背景噪声的信号十分丰富，在周期上至少跨越了7 个量级(0.03 s～105s)，它们以面波和体波的形式在地球表面和内部传播(Gutenberg，1931；Peterson，1993).学界通常将其中能量最强、周期范围约为2～20 s的部分称为“微震”(Microseism)，它具有两个明显的谱峰.一般认为，微震能量的产生源于两种不同的激发模式，周期12～20s的微震主要来源于海浪与海岸线和浅水区倾斜海底的直接相互作用(Hasselmann，1963)，因其频率与海洋重力波的频率接近，称为单频微震(Single Frequency，SF)，亦称为第一类地脉动；周期2～10 s的微震是在逆向扩散海浪之间的非线性相互作用下产生的(Longuet-Higgins，1950)，振幅要比单频微震大许多，其频率是单频微震的两倍，称为双频(Double Frequency，DF)微震，亦称为第二类地脉动.

关于微震的研究，尽管已经取得大量成果，但就其激发机制、源的确切位置以及传播特性等仍是热点问题.例如，关于微震能量的场源，是仅沿海岸线分布、还是也可在特定深海区域产生以及是否与风暴相关等，至今依然存在争论.多数研究认为SF微震来源于近岸区域(Gutenberg, 1931; Haubrich et al., 1963；Ardhuin et al., 2015； Bromirski, 2009；Friedrich et al., 1998)，但Stehly等 (2006)基于反向投影方法的研究认为，SF微震产生机理与更长周期背景噪声(20～40 s)的近似，来源于深海区，而非由海岸线上海浪的涌动所主导.DF微震的多源性则越来越被广泛接受，至少存在三种观点：(1)由近海海域的入射与反射海浪在近海海岸上的相互作用而产生(Cessaro, 1994；Bromirski and Duennebier，2002；Gerstoft and Tanimoto, 2007；Tanimoto, 2007；Stutzmann et al., 2012; Sun et al., 2013)；通过陆地和海底的对比观测与数值模拟，有学者指出DF的场源区主要为水深小于250 m的近海岸浅水区，在深度大于5000 m深海海底生成的pRg波其大部分能量蕴藏在海洋中，能在海底持续观测到，但不能有效地传递到大陆(Bromirski et al.，2013)；(2)由开阔海域海浪与局部水深相互作用形成的驻波产生，可能与体波激发的区域一致(Ardhuin and Herbers, 2013; Gerstoft et al., 2008; Landès et al., 2010; Tian and Ritzwoller, 2015)；(3)来自于风暴，产生于两个风暴形成的波浪，或由一个快速移动的大型风暴系统的两侧形成的波浪产生(Ardhuin et al., 2011；Obrebski et al., 2013；Chen et al.,2015).此外，在一些特殊地区观察到DF微震谱峰附近会出现两个或多个独特次峰的现象，正逐渐被关注并受到重视(Bromirski et al.，2005；Tanimoto，2007；Koper and Burlacu，2015；Xiao et al.,2018).

了解非随机持续性背景噪声的特性及其场源的确切位置，不仅对于提高背景噪声的产生机理的认识至关重要，同时还可以帮助改善相关应用研究的精度.越来越多的研究表明，真实背景噪声源分布的非均匀性及时变与理论假设之间存在巨大差异，这种差异会严重地影响经验格林函数的收敛程度与波形形态，特殊条件下甚至会致使噪声均匀分布的理论假设模型失效，从而导致所获得的背景噪声成像、介质波速变化测量结果等存在很强的不确定性(Zhan et al.,2013；Wang et al.,2020).另一方面，不同地区之间的背景噪声在能量强度、季节性时变规律等方面往往表现出强烈的地域特征(徐义贤和罗银河，2015)，这些区域性的差异同样也会在多个方面影响研究结果.目前，亦有不少学者基于不同的方法和观测数据，对我国部分地区的背景噪声能量强度(王俊等，2009；周连庆等，2017；杨千里等，2019；王芳等，2019)、噪声源的方向性(鲁来玉等，2009；王奡等，2017；王伟涛等，2011, 2012；Xiao et al.,2018；刘巧霞等，2020)以及与台风之间的关联性(夏英杰等，2011；郑露露等，2017)等开展过研究，但总体上大部分已有成果较少涉及微震能量从近海向内陆的传播扩散规律、瑞利波(Rayleigh)或勒夫波(Love)的横向偏振特性及其频率依赖性，尤其是场源的空间位置定位等.换言之，对于我国陆地及近海地区背景噪声特性的研究仍是不充分的，特别是对于非随机固有特性的研究更是相对缺乏.我国东部陆海相连的区域位置独特、地质构造环境复杂，为我们较全面地探究上述问题提供了天然的环境，近十年建设的高密度固定地震台网为开展精细研究奠定了数据基础.

本文将基于我国东部地区宽频带固定地震台站2015—2017年期间的三分量连续记录数据，运用频域偏振分析方法和背景噪声源定位技术，对我国东部陆地及近海地区稳定的微震背景噪声特性及其场源性质进行深入研究.研究结果可为深入了解我国陆地地区背景噪声的波场性质，揭示微震能量的产生机理与传播特性等提供依据.

1 数据与方法

1.1 数据选取

如图1所示，研究区的区位(112.5°E—125.0°E，28.0°N—41.5°N)，东临黄海、东海海域，西太平洋上风暴活动剧烈，西北部的渤海是内海海湾.陆地区域是由多个陆块拼贴组合而成的聚合性大陆，地质构造条件和地质地貌非常复杂，自北向南跨越了燕山地块、华北断块区、鲁东—黄海地块及华南地块等Ⅰ级地质构造单元，苏鲁大别超高压变质带、秦岭—大别造山带等；此外，区内展布的郯庐断裂带是纵贯我国东部的巨型断裂带，是一条切割莫霍面、深达岩石圈的深大断裂带(马杏垣等,1991;陈沪生等,1993;赵志新和徐纪人，2009;刘保金等, 2015；Li et al.,2020).这样多元的构造环境是研究微震背景噪声特性及其传播响应机制的天然理想场所.

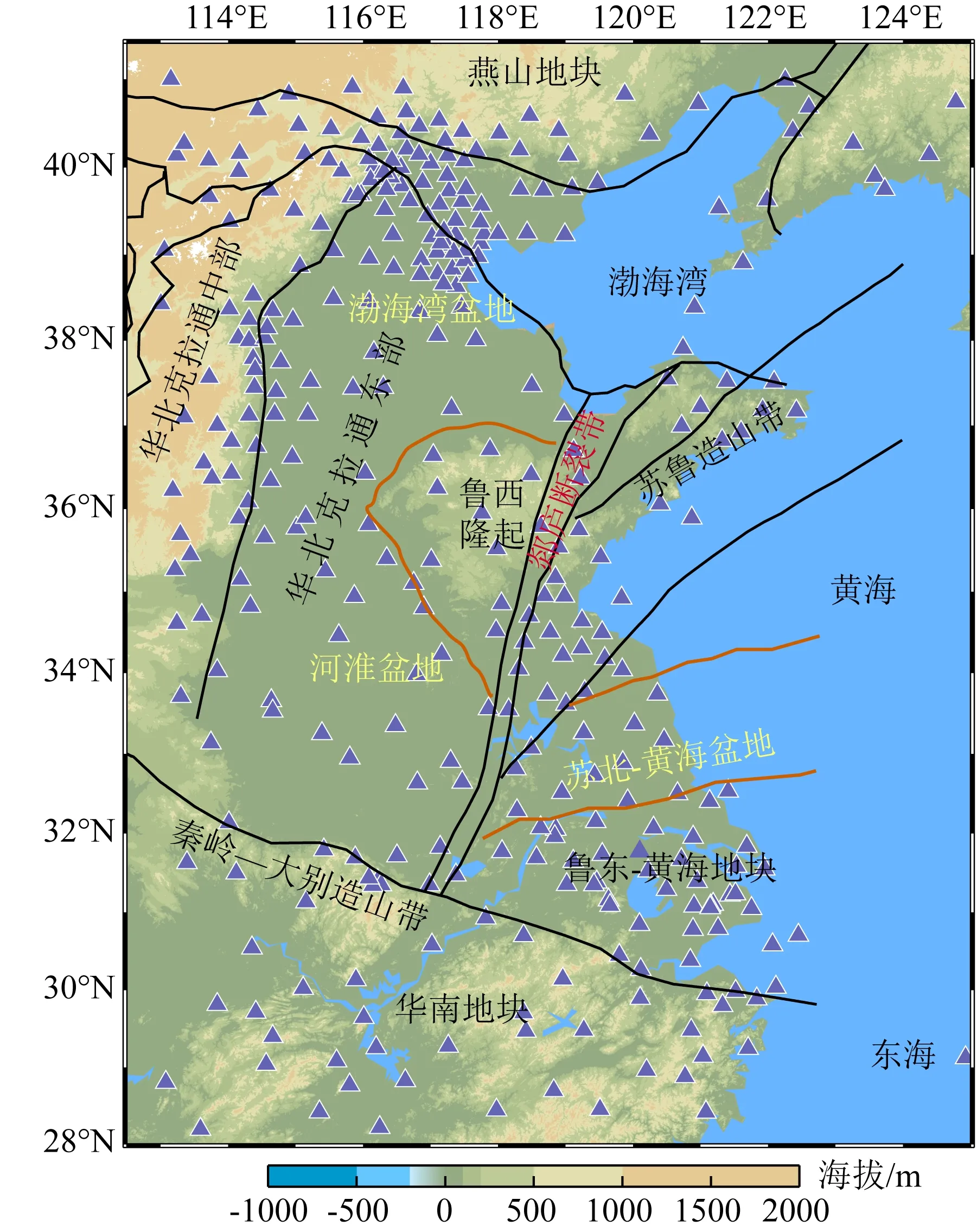
图1 本研究的区位、构造背景及所用台站分布，黑色 线条代表断层或块体分界线，三角形代表台站Fig.1 Geological map, tectonic setting and distribution of seismic stations used in this study. The black line indicates the boundary line of fault or block, triangular representative Station

本研究选取了我国东部地区共335个固定地震台站(图1)，时段为2015年1月—2017年12月期间的连续波形数据，数据来源于国家地震台网数据备份中心(郑秀芬等，2009)和相关省级地震台网.区内平均台间距约为30 km，其中地面型台站254个、井下型78个、海岛型3个；台站的数据采样率均为100 Hz，观测频带为360 s～50 Hz的台站2个、120 s～50 Hz的94个，60 s～50 Hz的208个、20 s～50 Hz的31个.所使用台站的三分向波形数据质量和完整性十分良好.据中国地震台网中心的年报结果：3年的数据完整率约为99.78%，台站台基环境背景噪声水平等级为Ⅰ、Ⅱ类的占比约为85%.

1.2 频域偏振分析

获取质点不同分量上的运动学特征和特性，偏振分析是最为经典且十分有效的技术.偏振分析技术的具体途径可以分为时域算法(Flinn，1965；Jurkevics，1988；林建民等，2012)和频域算法(Park et al.，1987；Samson,1983；陈赟等，2007)两类.本质上两种算法都是求解协方差矩阵的本征值问题，在滑动时间窗内计算特征值和特征向量，再由主特征向量及各种比值导出表征质点运动的各种属性，这些属性是与时间和频率相关的函数.频域偏振算法的优势在于，在直接获取信号频谱时，可采用长球体波函数来进行锥形化处理，互谱矩阵几乎不失真；互谱矩阵的平滑可通过叠加各分量的运动特征谱来实现，非常适合数据记录较短且信噪比较低的信号分析，其理论推导过程见Samson(1983)、Park等(1987)的研究，在此不做详细介绍.单台数据处理的步骤参照王俊等(2020)做法：三分量连续波形数据以1 h的长度为单个样本，首先对数据进行分段并进行锥形化，随后按50%的重叠比例滑动地计算三个分量的傅里叶变化(FFT)，进而基于每个子窗的平均频谱构建与频率相关的谱密度矩阵，矩阵形式是3×3的厄米特矩阵(Hermitian Matrix)；FFT计算的每个子窗长度取819.2 s，结果的有效频率范围为0.016～10 Hz.在计算前需对原始数据进行重采样(20 Hz)、扣除仪器响应等预处理.

通过谱密度协方差矩阵特征分解，可以获得其特征值(λ0、λ1、λ2)和相应的特征向量.本文采用Koper和Hawley(2010)改进后的计算程序，提取的参数包括：①最大特征值(λ0)对应特征向量偏振的功率，代表对原始三分量进行偏振分析后的主偏振的功率，简称为“主特征偏振功率”，与单个分量的功率谱密度近似，单位为加速度功率谱的分贝(dB，10×log10(m2·s-4/Hz))(Jepsen and Kennett,1990；Wagner and Owens，1996)；它能很好地刻画信号的振动能量，无论信号如何极化或者在三个分向上如何分割，其振幅在整个频段内始终可以被很好地捕获，如图2a所示，主特征偏振功率谱的幅值始终大于垂直(UD)、南北(NS)、东西(EW)三个分向的.②极化程度β2，见式(1)，表征信号的结构化程度，是无量纲参数，代表振动向量各个分量之间的相关度，在0～1之间变化；当所有特征值相等时，β2为0，而当仅存在一个非零特征值时，则β2为1.③ΘH，偏振椭圆的主轴方位，在0°～360°之间变化，代表瑞利波或P波等波源的反方位角(图2c).④径向与垂向分量的相位差φVR，在-90°～90°之间变化.ΘH与φVR之间存在等效效应(Koper and Burlacu，2015)，例如：对于来自某一特定反方位角(ΘH=45°)的逆向瑞利波(φVR=-90°)可以等效地被描述为来自于反方向(ΘH=225°)的正向瑞利波(φVR=90°).

(1)

S为谱密度矩阵，n为数据序列长度，Tr为非负数约束条件下的最小化因子，详见Samson(1983)的(31)式.

1.3 单台偏振特性提取

研究表明，从单个弱偏振噪声子窗内测得的偏振量值并不十分稳定(Koper and Hawley，2010)；另一方面，连续记录数据中地震事件、系统标定、环境干扰等低概率瞬态信号，也会对计算结果造成影响.因此，要捕获台站噪声场源的非随机特性，只有基于对长时间尺度的大量测量值进行分析才具有实际意义.本文采用概率密度函数方法(McNamara and Buland，2004)，通过提取上述各个参数在2015—2017年期间内最大概率分布值，来表征噪声场源的固有属性.根据1.2节中的数据处理方法，单台理论上每天有48组偏振分析结果；剔除数据中断等异常情况，统计显示，研究区内单台3年内的平均结果约达52160组.如图2(b、c)江苏海安台的概率密度分布结果所示，低概率的瞬态信号和季节性扰动被明显弱化，而固有的微震信号则明显增强，于是从中提取的最大概率分布特征能很好地表征该台的固有属性.

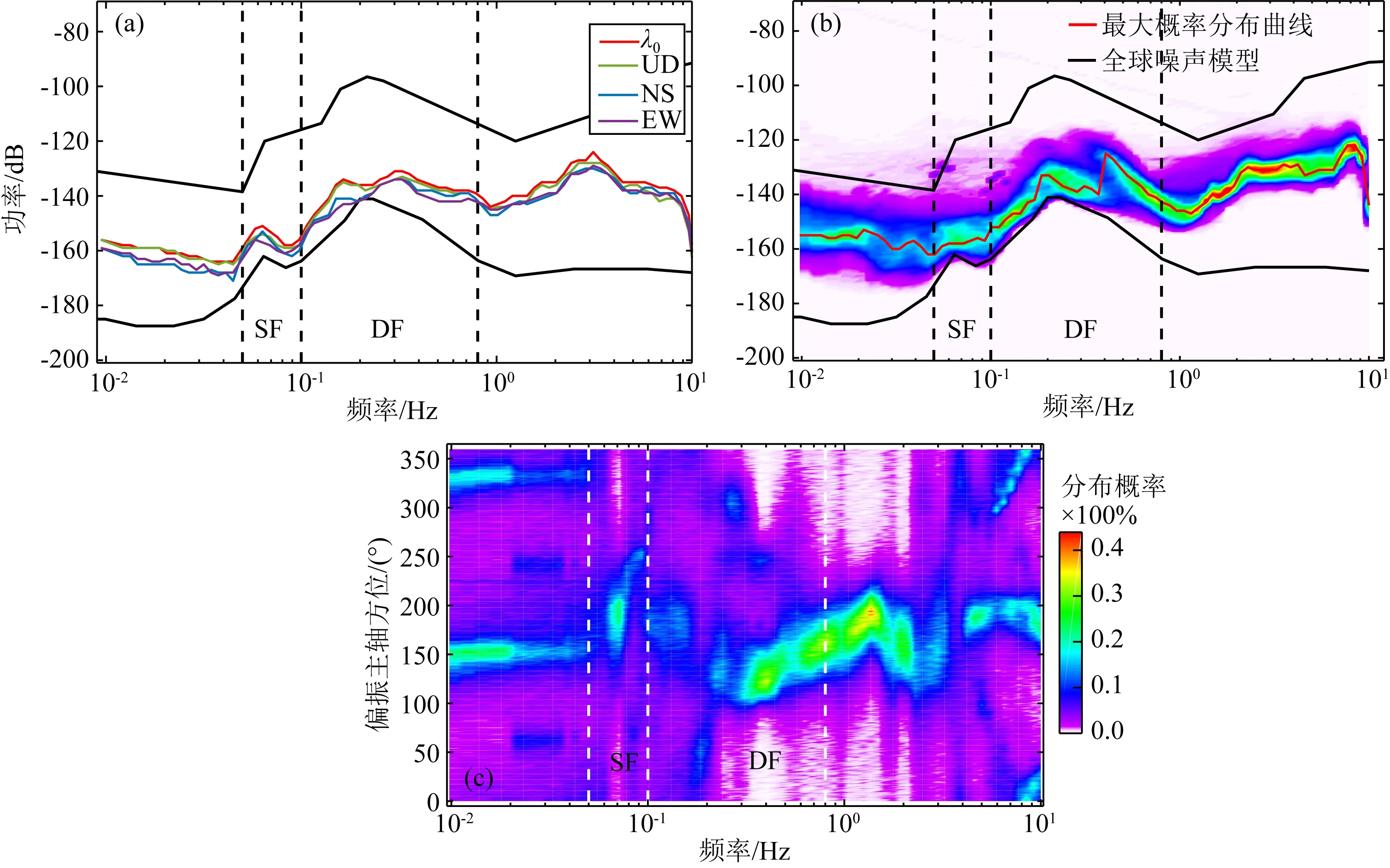
图2 单台频域偏振分析结果 (a) 单子窗内背景噪声主特征偏振与原始三分量的功率对比; (b) 2015—2017年主特征偏振功率的概率密度分布; (c) 2015—2017年偏振主轴方位的概率密度分布.Fig.2 The results of frequency-dependent polarization analysis for a single station in JS.HA station (a) Comparison of the power of principal eigenvalue polarization and original three components in a single sub-window; (b) The probability density distribution of the power of principal eigenvalue polarization during 2015—2017; (c) The probability density distribution of polarization principal axis azimuth during 2015—2017.

2 结果分析

2.1 背景噪声场源的非随机性

本文成功计算了研究区内335个台站的结果，结果表明，就某一固定地震台站而言，尽管微震频段的背景噪声主特征偏振功率在短时间尺度内(如天、月等)存在明显的波动，但在较长时间尺度(1年以上)内其能量场是相对稳定的，即使是DF微震亦是如此，其固有特性主要取决于非随机稳定的微震噪声源性质及台站所处的地质环境.如图3江苏海安台的计算结果所示，该台距离海岸线约50 km，从2015—2017年期间主特征偏振的时频分布特征看，不同年份间微震频带(0.05～0.5 Hz)内的能量是较为稳定的，主特征偏振功率谱谱峰频率的中位值分布形态基本一致(图3b)，单天的结果是当日的最大概率分布值，双峰特征并未改变，基本稳定在0.2 Hz和0.33 Hz附近.这意味着，年尺度的主特征偏振的功率和峰值频率是相对恒定的.同时注意到，2015—2017年间在西太平洋上中心风力大于10级以上的风暴活动区域与路径并不一致，相较而言，2015年的风暴活动情况比2016、2017年剧烈，对比发现该台的谱峰频率中位分布仅在0.2 Hz附近的有轻微改变；据此认为风暴对台站DF微震背景噪声固有特征的影响程度是有限的.此外，研究区内近岸台站的DF谱的双峰特征较为普遍，与江苏海安台近似，能量主要集中在0.1～0.25 Hz、0.25～0.6 Hz频段内，参照已有研究，分别称为长周期双频微震(LPDFMs)、短周期双频微震(SPDFMs).

图4a是3年尺度SPDFMs主特征偏振功率谱峰值的空间分布，可以看出功率谱强度基本上随距西南方向海域海岸线的距离变近而逐渐减小；从沿经线方向的剖面分布看(图5a)，台站由近海岸向内陆纵深展布的过程中其主特征偏振功率逐渐减小的特征更加明显，东西两端相差约达25 dB.这符合近岸涌浪作用是影响SPDFMs能量支配控制因素的预期.进一步地，依据各台站距海岸线最小距离与SPDFMs主特征偏振功率强度的对应关系看(图5b)，其强度的几何扩散趋势粗略地接近于面波二维扩散模式下振幅以近似1/r衰减的规律.采用万永革(2016)的方法，模拟的点源模型下各向同性均匀介质下球面波传播振幅随距离的扩散趋势，如图5b蓝色线条所示：

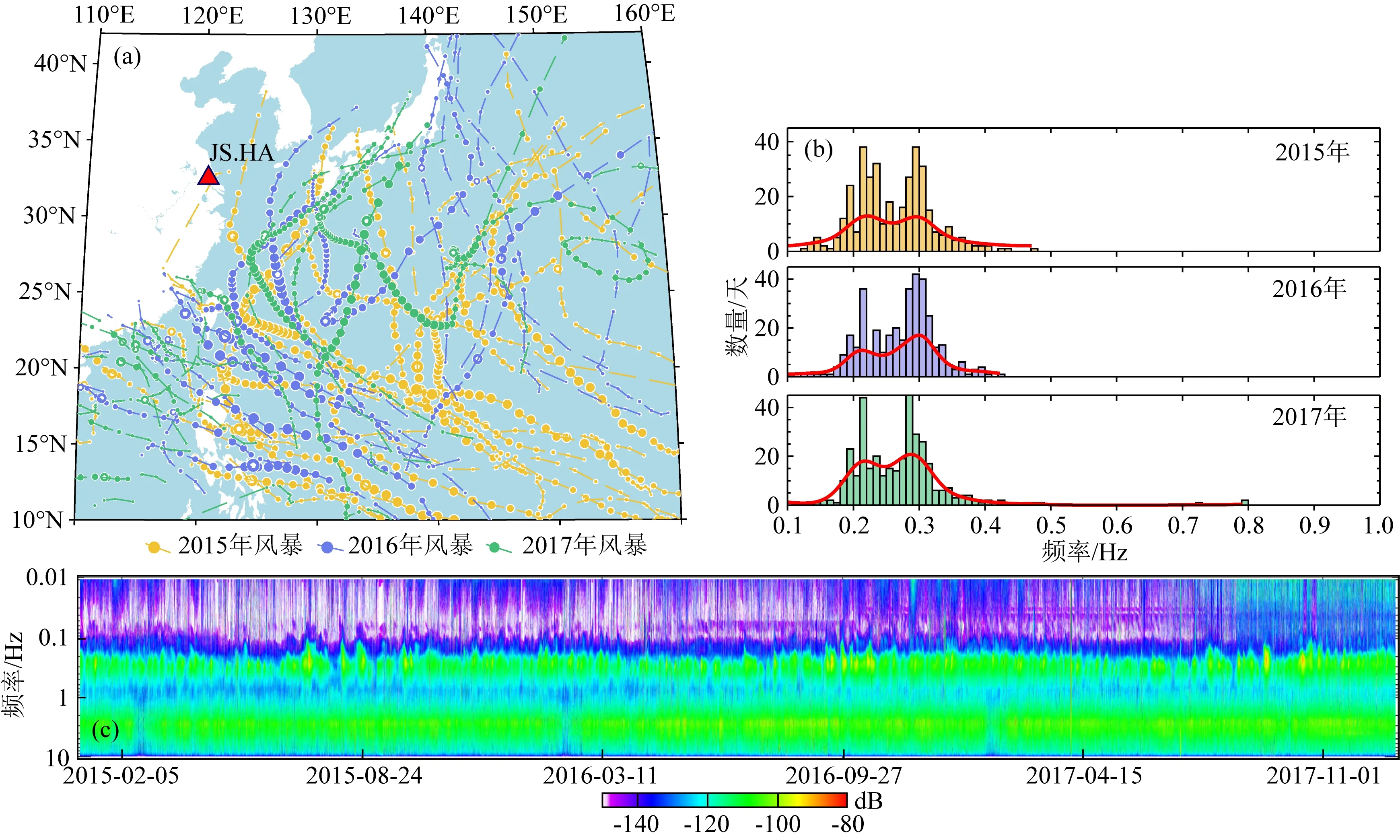
图3 江苏海安台2015—2017年间的计算结果 (a) 西太平洋上中心风力大于10级的台风活动路径； (b) DF微震主特征偏振功率谱峰值频率的中位； (c) 主特征偏振的时频分布.Fig.3 The calculation results of JS.HA station from 2015 to 2017 (a) The tracks of typhoons with central winds greater than force 10 over the Western Pacific; (b) The median of peak frequency of principal eigenvalue polarization for DF microseisms in different years; (c) Time-frequency distribution of principal eigenvalue polarization.

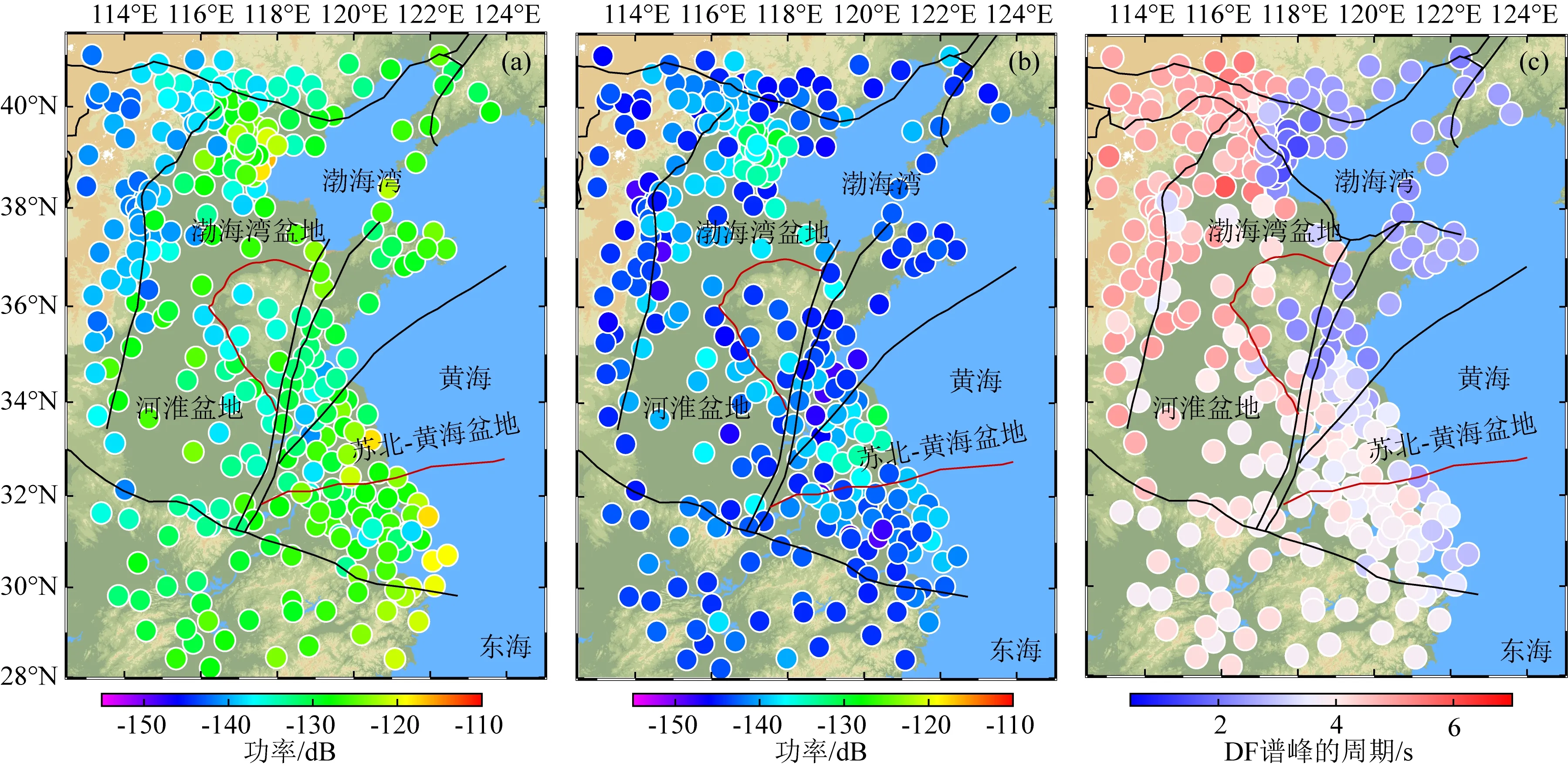
图4 SPDFMs(a)、LPDFMs(b)主特征偏振功率峰值及DF微震谱峰周期(c)的空间分布, 每个圆代表一个台站Fig.4 Spatial distribution of the power peak of the principal eigenvalue polarization for SPDFMs (a), LPDFMs (b) and period of DF spectrum peak (c)，each circle represents a station

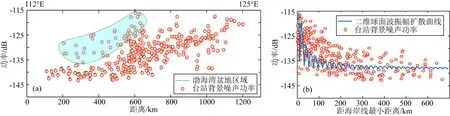
图5 (a) 主特征偏振功率峰值沿经线视角剖面的分布； (b) 台站距海岸线最小距离与主特征偏振功率峰值的分布关系， 蓝色曲线为模拟的球面波传播振幅扩散曲线Fig.5 (a) The distribution of the power peak of the principal eigenvalue polarization along the longitudinal viewing angle profile; (b) The relationship between the minimum distance from the station to the coastline and the spectral peak power, and the blue curve is the simulated spherical wave propagation amplitude-spread relationship

(2)

φ(r,t)表示由源向外传播的面波振幅，是时间t(单位为s)和震中距(r，单位为km)的函数；ω为角频率(2×π×f)，f=0.2 Hz；α为面波的波速，取3.0 km·s-1，A为r=0时的振幅值，取主特征偏振功率实测的最大值(-110 dB).

图4b是LPDFMs主特征偏振功率谱峰值的空间分布，未显示出与SPDFMs相似的特征，则是与台站所处地质环境条件的关联性十分密切，高值区主要集中于渤海盆地北部和苏北—黄海盆地松散沉积层覆盖区，次高值区为淮河盆地.研究表明，由近海产生的瑞利波及勒夫波的能量会被转化成垂直扩散的横波能量，可在数千米厚的低速沉积层中回弹并增强微震能量(Benz and Smith，1988；Langston et al.，2009)；如苏北—南黄海盆地就存在这样近似的环境，其早第三纪沉积层厚达6 km(杨琦和陈红宇，2003).此外，加利福尼亚州和日本的小范围沉积盆地也已曾观察到过DF增强现象(Kagami et al.,1982；Yamanaka et al.,1993；Dolenc and Dreger，2005；Koper and Burlacu,2015).然而，从本文结果看，在盆地内观察到的能量增强现象，很可能仅限于LPDFMs频段，并非整个DF频段.

从图4c的DF微震主特征偏振功率谱峰值周期的空间分布看，谱峰周期值约在1.6～6 s之间变化，随着距海岸线距离的增加谱峰周期值逐渐增大.谱峰周期的高值区域位于研究区西北部的华北克拉通中部区域，在东北部近似形成一个以渤海湾为中心的圆型低值特殊区域，峰值周期平均仅约2 s，明显低于其他区域；研究区中南部毗邻黄海和东海海岸线向内陆部延伸区域的台站峰值周期变化幅度的连贯性更好.总体上呈现渤海湾水体对近岸台站背景噪声DF微震的影响明显强于开放型近海海域的特征，或者说特殊的海湾环境使得海浪的反射变得更加复杂，增强了SPDFMs的振幅.如图5a所示，可清晰地看到渤海湾区域的主特征偏振功率强度平均增加了约10 dB左右.海浪较低区域也有激发能量较强DF微震的可能性(Euler et al.,2014)，因为在浅水中反射的(相反作用)振幅可能更大，并且其中生成的DF能量会产生大部分易于在内陆传播的弹性pRg波.据Bromirski 等(2013)研究认为，海浪重力波长500 m约对应微震信号的周期为18 s，渤海湾的平均水深约18 m，其波浪重力波相互作用产生的微震周期应小于2 s，与该区域SPDFMs峰值周期小于2 s的实际相符.

2.2 背景噪声场源的方向性

图6给出了研究区内各台站3年时间尺度叠加后的偏振主轴方位(ΘH)结果.空间最大概率分布结果显示：对于SF微震(12～20 s)，大部分台站(约81%)的偏振主轴方位主要分布在160°～240°之间，优势方位约为221°，意味着我国东部地区SF微震的主要来源并非是毗邻的东部海域方向，而是可能来自于更远的区域，这与一般认为其主要来源于可能是东南方向西太平洋的预期稍有不同，偏振主轴的优势方位沿大圆弧路径的投影指向位于西南方向的印度洋(图6c).有学者使用华北科学台阵探测到周期约为16 s 的瑞利波慢度谱极大值分布方位集中在120°～220°范围，能量强度夏季大于冬季，勒夫波的方向性则相对较弱(鲁来玉等，2009).不过，更多的研究指出印度洋方位存在较为稳定的瑞利波 10～20 s信号，在我国西北、云南以及中部地区也都观测到过，且具有季节性变化特征(刘巧霞等，2020；王芳等，2020；王伟涛等，2011).SF微震的频率与波浪对应，而波浪运动产生的垂向压力随水深的增加而呈指数衰减，因此一般认为SF微震的主要源区分布在浅海海域；但Stehly等(2006)指出其源很可能来自于大洋深水区的涌浪作用.因此，本文观测到SF微震能量具体是来自于孟加拉湾、还是印度洋中心的浪高区域，需要进一步研究确认.从图7了解到，其φVR概率分布较为宽泛，β2也处于较低的水平，在0.1～0.2之间，表明SF微震在垂向和切向上的运动学特征差异不明显，主特征向量并不是纯态瑞利波，而很可能是一种瑞利波、勒夫波和体波的混合.最近的研究认为，印度洋的南半球大洋的运动特点更为显著(Gal et al.，2015；Liu et al.，2016).因此，我们推测印度洋方位的噪声源同样也是我国东部地区SF微震噪声的主要场源，并非仅影响我国的西部地区，甚至很可能是一个全球性的噪声场源区.

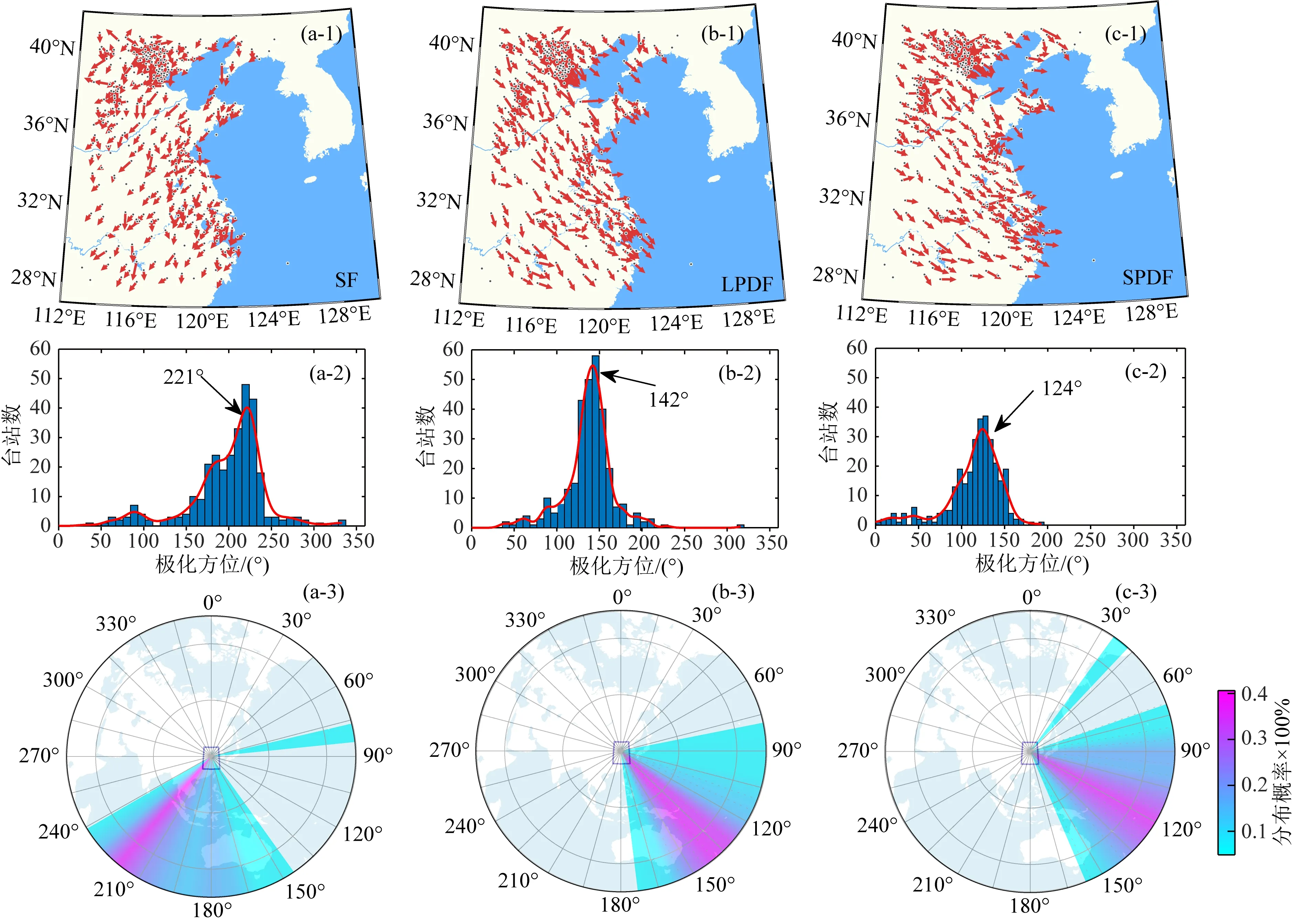
图6 研究区台站的偏振主轴方位 (a) 偏振主轴方位与极化程度加权的空间分布，极化程度越高箭头长度越长； (b) 偏振主轴方位值的柱状分布； (c) 偏振主轴方位在空间上的概率值投影.Fig.6 Results of polarization principal axis azimuth of stations in the study area (a) Spatial distribution of polarization orientation weighted by polarization degree. The higher the degree of polarization, the longer the length of the arrow; (b) Cylindrical distribution of azimuth values of principal axes of polarization ; (c) Probabilistic projection of the azimuth of the principal axis of polarization in space.

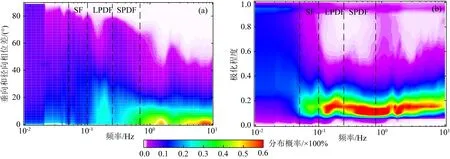
图7 φVR (a)与β2(b)随频率的概率密度分布，由2015—2017年研究区内所有台站的叠加获得Fig.7 Probability density distribution of φVR (a) and β2 (b) with frequency. It is obtained from the overlying of all stations in the study area during 2015—2017

DF微震的偏振主轴方位集中在80°～170°之间，指向东南方向海域，基本符合DF微震能量主要由近海生成机制所主导的预期，产生于入射波能和海岸反射/散射波能之间的相互作用(Longuet-Higgins，1950；Cessaro, 1994).也与全球其他地区的研究结果近似，如美国西南部的DF偏振向量与加利福尼亚州南部及墨西哥巴哈的海岸线有关，佛罗里达州及中大西洋各州的DF偏振向量向东与距离最近的海岸线有关(Koper and Burlacu，2015).然而，进一步观察发现， LPDFMs与SPDFMs偏振主轴方位的覆盖范围虽然基本一致，但是它们的优势方位略有不同，分别约为142°、124°，主要原因是SPDFMs偏振主轴方位在30°～100°之间的台站占比偏多(图6c2)，指向渤海湾和东部近海岸线方向；空间分布上，这类台站主要分布于海岸线附近.研究表明，近海岸或海岛地区0.12 Hz以上信号主要受周边海域波浪(Bromirski and Duennebier，2002；陈栋炉等，2018)影响.从图7的结果看，DF的φVR、β2虽也处于较低水平，但在0.25 Hz附近的分段特征非常明显，说明两者在垂向和径向上振动特性并不完全一致，能量产生机理不完全一样，应该具有不同的场源，LPDFMs垂向上的振动向量较强，瑞利波成分具有相对优势，而SDPFMs则是勒夫波成分相对较多.我们相信，过去在解释DF微震产生机理方面存在的一些不确定性，很可能一定程度是因DF微震谱峰的分叉造成的，由于以往大多数研究并未使用大量高频段内的数据来进行研究.由此推测，我国东部地区的DF微震至少存在两个较为稳定的持续性场源是可信的，其中LPDFMs可能产生于开阔近海海域海浪与海底的相互作用，开阔海域上的飓风/风暴活动能对其产生一定的影响，但不起支配地位.SPDFMs则可能源自于我国近海区域内的波-波相互作用，导致在海岸线附近存在另一场源；Ardhuin等(2011)认为这种波-波相互作用就年尺度是十分稳定的.

此外，我们还观察到各台站SF微震偏振主轴方位与总的优势方位(221°)之间偏差明显的区域，不仅限于海岸线附近，位于内陆块体边界过渡带附近台站的变化幅度也总体大于稳定地块内的(图8).一般而言，若传播方向变化过大则说明面波对传播路径有很强的依赖性(Liu and Holt，2015；周鲁等，2017)，这种依赖性很可能是传播过程中经历较为显著的横向结构变化而造成射线路径改变所引起的.研究表明，板块边界的速度差异可达0.25 km·s-1，能引起较大的传播方位变化(Liang and Langstong，2009).对于地震事件的记录而言，长周期信号偏振方位变化主要是入射波场产生的，因此通过高密度台站观察到的方位差变化，或许可为研究重要地块的边界特征提供另一视角的信息，值得结合面波传播的多路径问题进一步深入研究.

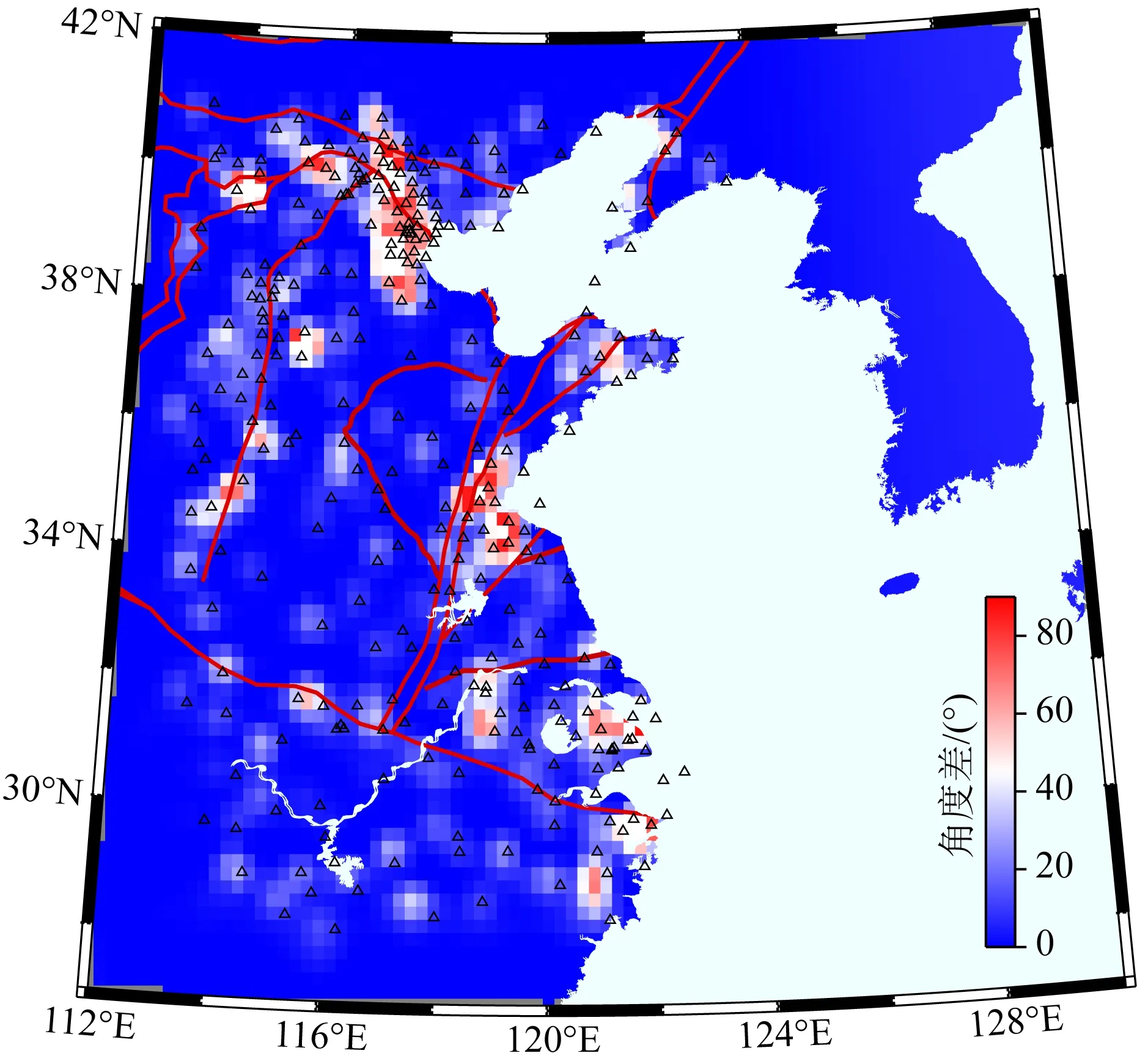
图8 SF微震偏振主轴方位差空间分布，红色线条 代表断层或块体分界线，三角形代表台站Fig.8 Spatial distribution of polarization principal axis azimuth difference of SF microseismic. The red line indicates the boundary line of fault or block, triangular representative Station

2.3 噪声场源的空间位置与激发机制

从上述结果可知，我国东部地区微震频段内的能量是存在较为稳定的来源，且具有明显的方向性，其空间分布既不均匀也不随机.为较准确地确定噪声场源的位置，本文将针对大尺度固定地震台网，尝试发展一种基于非对称性能量走时差来构建目标函数的格点搜索定位方法.非均匀持续性噪声源的存在会使得在台站对两个方向传播的能量总和不均等，从而造成互相关格林函数在正与负流逝时间内信号振幅的非对称(Stehly et al.，2006).如图9b所示，研究区内实际的互相关格林函数，在大多数路径上的能量非对称性十分明显，反映出研究区整体噪声源是偏向海洋的(如视速度3.0 km·s-1的非对称性)，同时在常规面波信号前出现的由持续性噪声源产生的非对称信号也十分清晰.在互相关格林函数中，视速度小于20 km·s-1面波信号中有3个明显的峰值，周期约为5 s、10 s、16 s.其中，周期约为5 s左右的信号其P波能量显著增强、面波能量减弱，可视为体波(王芳等, 2020)；而周期为16 s的为瑞利面波，但信号能量较弱，准确定位较为困难，本文将暂不讨论.周期约为10 s的信号能量最强，是瑞利波之前的前驱信号，我们将对这类源进行定位，并探讨其激发机制.假设点(x,y)处的噪声源在互相关格林函数Cij中产生一个信号，可以通过其理论走时差Tij与实际走时差tij来构建如下目标函数(Shapiro et al.,2006)：

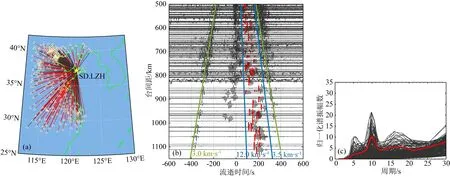
图9 SD.LZH台的噪声互相关函数处理结果 (a) 台站对间的路径分布； (b) 由3年数据叠加获得的互相关格林函数，红色短线为自动拾取走时差的位置; (c) 互相关格林函数的周期谱.Fig.9 Processing results of noise cross-correlation function for SD.LZH station (a) Paths between pairs of station; (b) Cross correlation Green′s function superimposed by 3-year data, the red short line is the automatic picking position of shifting time; (c) Period spectrum of cross-correlation Green′s function.

(3)

目标函数的最小分布位置即为噪声源的潜在位置.对于面波型噪声源，假设面波信号是以速度U(3.0 km·s-1)均匀传播的，该信号的Tij可以表示为

(4)

其中di(x,y)和dj(x,y)分别表示两个台站到噪声源的距离.实际测量过程中，由于需要处理近10万条互相关格林函数，为减少走时差拾取误差，我们引入AIC震相到时拾取方法来自动拾取走时差(Leonard，2000).鉴于面波的初始位置并不十分明显，为提高定位结果的可靠性，仅拾取台站对间距大于200 km、视速度范围3.5～12 km·s-1且信噪比大于20的非对称性面波振幅的走时差.如图9b所示，以SD.LZH为例，满足条件的自动拾取结果共有243个，与人工拾取结果对比，拾取误差在3 s以内的比例约达92.4%.

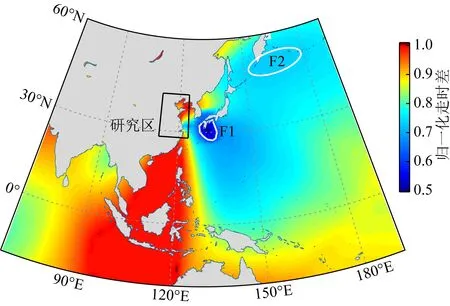
图10 持续性背景噪声源(10 s)的空间位置Fig.10 Possible spatial locations of noise sources with a period of about 10 s

图10是在地球表面网格间距为0.5×0.5°情形下的搜索定位结果，目标函数的低值区主要分布于太平洋方向(F1、F2)，其中极低值区F1位于九州岛上的ASO火山附近区域，与Zeng和Ni(2010)、王伟涛等(2012)采用幅值能量累加搜索方法获得的位置十分接近，表明本文的定位结果是可靠的.由该火山持续性震颤(Volcanic tremor)所产生的周期约10 s信号在日本西南较大范围均能观测到(Kawakatsu et al.,1994)；这进一步地验证了ASO火山的持续性震颤是我国东部地区周期为10 s信号主要来源的推测.但从空间上看，本文定位的区域与已有定位结果相比，范围要更大一些，涵盖了九洲岛并扩展至部分外海区域，这一方面可能是由于搜索定位采用平均速度模型和自动拾取面波到时与真实值之间存在误差，所引起的定位偏差所致；但另一方面，ASO火山噪声场源是否是确切的点源也需更进一步研究，因为场源区正好位于日本本岛与南部岛链共同形成的 “Y”型区域中间，也不能排除ASO火山噪声场源在外海海浪的影响下形成共振，使得噪声场源区域有所扩大的可能.F2区则主要位于北太平洋的深海区，其位置与Gerstoft等(2008)、Kedar等(2008)、Landès等(2010)采用不同方法获得的定位结果基本重合；该区域也是太平洋上体波的激发场源区，其可能的机制是由深海区非线性的波-波相互作用或独立波浪系统所产生的.

3 结语

本文基于我国东部大规模固定地震台站的连续波形数据，获取了我国东部地区非随机稳定性微震背景噪声源的特性以及空间位置，并对其激发机制进行了深入分析.要刻画地震背景噪声非随机且稳定的特性，关键在于排除噪声源的季节性变化及其他随机性干扰，本文基于海量偏振分析结果，采用概率密度函数方法很好地捕获到微震背景噪声能量在空间分布及传播扩散等方面的特性.为进一步探究噪声源的激发机制，针对大尺度地震台网，发展了一种基于非对称性能量走时差构建目标函数的格点搜索定位方法，对非随机性噪声源进行定位，与已有研究成果对比，本文的定位结果具有较高的可靠性.获得以下几点认识：

(1)我国东部地区的微震能量场，其年尺度以上的固有特性主要取决于非随机性的微震噪声源的性质及台站所处的地质环境.研究区内近海岸台站的主特征偏振功率谱在0.25 Hz附近出现双峰或多峰的现象十分普遍；大陆型台站与近海岸台站相比，DF谱峰的频率和功率值都要更低，认为主要是由于海岸的散射及转换会造成传播能量损失所致.SPDFMs主特征偏振功率强度的扩散规律与距海岸线的远近有密切的相关性，主要支配控制因素是近岸涌浪作用；渤海湾水体对其周边近岸台站DF微震特性的影响强于开阔型近海海域，渤海湾毗邻区域的主特征偏振功率谱峰值总体高于其他区域约10 dB左右，推测认为是海湾的独特地形使得海浪的反射变得更加复杂，进而增强了SPDFMs的能量所致.LPDFMs主特征偏振功率的空间分布特征与台站所处地质环境的关联性更为密切，功率高值区主要集中于盆地或松散沉积层覆盖区.

(2)研究区内非随机持续性SF微震噪声源的方位主要指向印度洋方向.近年来的其他研究也表明，位于南半球印度洋南部至南极洲之间的深海区很可能稳定存在周期约16 s的噪声源，该区域也是P波噪声源区.从偏振特性看，在SF微震频段内垂向和切向上的运动学特征差异不显著，主特征向量并不是纯态瑞利波.推测认为，影响我国东部地区的持续性SF微震噪声源，很可能位于印度洋中心的浪高深海区域，是由海浪驻波作用于远海海底所激发产生，而非作用在近海海岸或大陆架所产生.

(3)研究区内非随机持续性DF微震噪声源的方位整体指向东南的太平洋方向，但LPDFMs与SPDFMs之间的优势方位略有不同，它们的β2在0.25 Hz附近存在明显的分段特征，说明两者在垂向和径向上振动特性并不完全一致，LPDFMs垂向上的振动向量较强，瑞利波成分具有相对优势.激发机制方面，LPDFMs很可能产生于开阔近海海域海浪与海底的相互作用，开阔海域上飓风/风暴的活动对其影响有限；SPDFMs则可能源自于我国近海区域内稳定波-波相互作用形成的另一场源.

(4)微震频段内主要的持续性噪声源其周期约为10 s，很可能位于九州岛上的ASO火山附近；但本研究的定位结果区域较以往研究者的范围稍大，不排除ASO火山噪声场源在外海海浪的影响下形成共振，进而使得噪声场源区域有所扩大的可能；另一个持续性噪声源则可能位于北太平洋的深海区.

致谢感谢审稿人宝贵的建设性意见，本研究使用的大部分连续波形数据来自于中国地震局地球物理研究所国家测震台网数据备份中心，台风活动路径数据来自于https:∥www.ncei.noaa.gov/data/，偏振分析计算程序来自于http:∥ds.iris.edu/ds/products /noise-toolkit/，在此一并感谢.