基于深度学习的变换器宽范围暂态等效建模
2022-05-05胡博杨超田小蕾李云路杨俊友崔嘉
胡博,杨超,田小蕾,李云路,杨俊友,崔嘉
(1.国网辽宁省电力有限公司,辽宁 沈阳 110004;2.沈阳工业大学电气工程学院,辽宁 沈阳 110870)
随着并网电力变换器的广泛应用,电力系统的惯性开始逐渐下降,电力变换器在接入点的暂态过程也呈现逐渐复杂化的趋势。变换器在接入点的动态特性越来越容易受到外部扰动的影响,使其暂态过程难以预测[1-2]。因此,对电力变换器的暂态等效模型进行研究,可以准确预测系统暂态过程,分析系统暂态稳定性,可以通过仿真提前验证变换器接入性能,避免实际应用中可能出现的事故[3]。
现有的变换器暂态等效模型的方法是根据其全部参数和控制拓扑,建立对应微分代数方程组(differential algebraic equations,DAEs),通过进行时域仿真进行暂态过程计算[4]。然而,在实际应用当中,系统的参数,甚至控制拓扑无法全部知晓。导致这一情况的原因可能是商业机密、设备供货商退出市场、设备陈旧导致参数发生变化等等[5]。这使得建立DAEs的方法多数情况下无法实施。
为了在上述情况下进行暂态等效建模,学者们进行了大量的研究工作。基于频率扫描的阻抗建模方法是目前广泛应用的方法[6]。通过观测变换器端口电流在不同频率端口电压下的响应,建立对应的变换器等效阻抗模型[7]。与这种方法类似的还有基于Prony分析的方法[8]。虽然频率扫描类的方法能够解决黑盒建模问题,但是其本质上是基于傅里叶变换的线性建模方法。而电力变换器是包含多个非线性环节的系统。因此,所建立的模型是只在单一工作点有效的小信号模型。当工作点发生变化时,所建立的线性模型失效。这意味着此类模型在大扰动下(如短路故障)无效。
另一种常用于解决参数未知建模问题的方法是基于系统参数辨识的方法。当系统拓扑结构已知而参数未知时,通过测量系统的输入输出,对系统的参数进行矫正,以实现参数辨识[9]。本质上这是一种灰盒建模方法。但在实际工程当中,系统的拓扑结构存在未知的情况。研究人员通过将系统结构等效成多阶线性状态方程的形式实现参数辨识[10-11]。然而,这种用线性系统区等效非线性系统的方法也存在着只在单一工作点有效的问题。所建立模型在大扰动下仍然失效。
近些年来,人工神经网络在能源技术领域得到了快速的发展和广泛的应用。多种神经网络被用来解决电气系统建模问题。大多数神经网络(如径向基神经网络)被用来解决系统的非线性特性建模问题,取得了不错的效果[12]。随着深度学习技术的发展,基于循环神经网络(recurrent neural network,RNN)的方法也被用来进行系统的长时间尺度时间序列预测问题[13-14]。但已有的基于神经网络的方法尚缺少对并网变换器短时间尺度下暂态过程建模的研究,也缺乏选择神经网络建模的依据的讨论。
受到DAEs与RNN在数学角度具有等效性的启发,本文提出一种基于门控单元(gate recurrent unit,GRU)RNN的电力变换器暂态等效建模方法。首先,从数学角度对选择RNN进行建模的原因进行分析。然后,对建模过程进行详细的阐述。最后,通过大扰动下的暂态过程仿真,验证方法在宽范围内有效。
1 变换器暂态模型
对于传统电力变换器来说,一般具有如图1的系统结构。

图1 电力变换器结构Fig.1 The structure of power converter
电力变换器在d-q坐标系下的暂态模型表达式可以有如下表达:
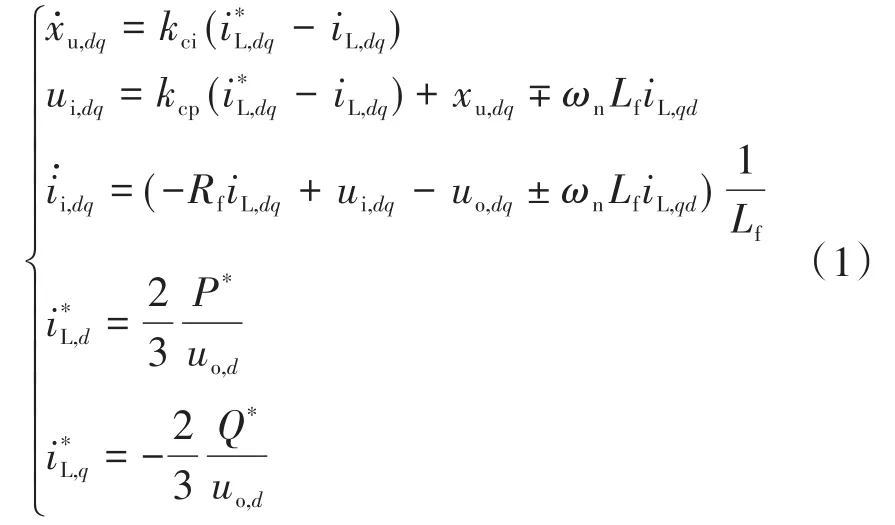
式中:Rf,Lf为注入电感的电阻和电感值;P*,Q*为变换器的输出参考功率;为电流控制器的参考输入,其经过电流控制器后产生逆变桥控制电压信号ui,dq;kcp,kci为电流环 PI控制器的比例系数和积分系数;PCC 为变换器接入点;iL,abc,uo,abc分别为PCC处采集的三相瞬时电流、电压,经过d-q变换得到iL,dq和uo,dq;xu,dq为电流控制器中积分环节包含的状态转移变量。
从式(1)可知,电力变换器的暂态模型可以视为微分-代数方程组,可以概括为如下表达:
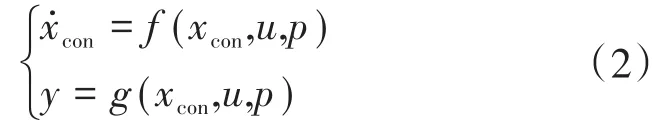
式中:f为广义函数表达式;xcon为广义状态转移变量;u,y为系统输入、输出;p为系统所含参数。
2 基于GRU的深度神经网络
本文所提出的方法是一种新的变换器动态等效建模方法,将P*,Q*,uo,αβ作为神经网络输入,iL,αβ作为神经网络输出,建立基于深度RNN网络的动态等效模型。单个RNN神经元如图2所示,其中x(t)和o(t)是网络的输入和输出的时间序列;σ(.)和φ(.)是激励函数,通常分别是sigmoid(.)和tanh(.)函数;s(t)是RNN单元在t时刻的状态;U,V,W是神经元的权重矩阵。bo,bs是神经元的偏置矩阵。
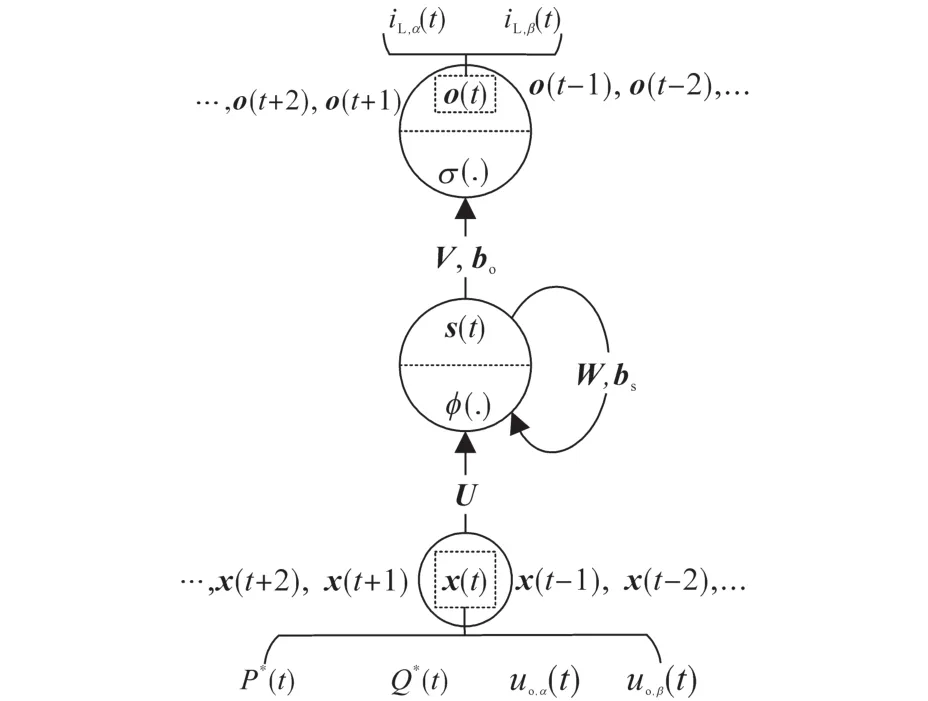
图2 RNN神经元结构Fig.2 The structure of RNN neuron unit
当时间序列x(t)输入到RNN单元当中,会进行如下运算:
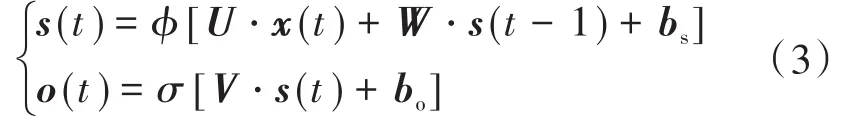
由式(3)可以发现,RNN的状态同样影响着RNN的输出,RNN可以被视为一个离散动态系统,可以被用来进行动态系统的黑盒建模。但RNN在训练网络的过程中存在梯度消失和梯度爆炸的问题,很难得到理想的模型。因此,GRU神经元被提出用来克服RNN在训练中的这两个问题,其结构如图3所示。
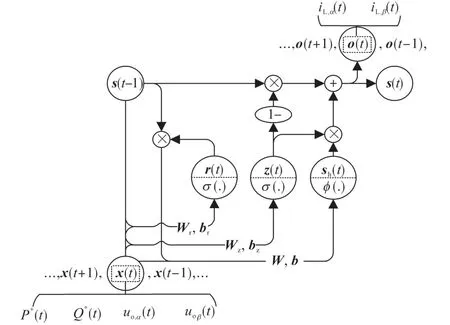
图3 GRU神经元结构Fig.3 The structure of GRU neuron unit
GRU神经元的计算如下:

可以发现,上一时刻的系统状态同样可以影响到当前时刻的输出,GRU同样可以被视作离散动态系统。那么对于一个由多个GRU单元和常规全连接神经网络层(full-connected layer,FC layer)组成的RNN网络,可以表达为如下形式:

式中:Wm,bm为 GRU层的神经元参数矩阵;Wf,bf为FC层的神经元参数;F,G为广义函数表达式。
式(5)、式(6)可以分别视为离散的微分方程和代数方程。同时,对于一个未知的变换器动态系统,可以有如下形式:

式中:x,u,y,p分别为变换器系统状态、输入、输出和参数。
通过对比式(5)~式(6)和式(7)~式(8)可以发现,基于GRU的RNN网络可以被视为黑盒的离散DAEs,本文所提出方法的实质就是通过建立基于GRU的RNN网络去拟合黑盒的DAEs来实现变换器系统的黑盒暂态建模。
3 网络模型设计要点
3.1 模型数据
对于使用神经网络进行黑盒建模问题来说,准备网络模型的训练数据是重要的一步。为了建立变换器的暂态等值模型,变换器接入点的瞬时电压、电流信号被记录下来。为了简化数据结构,三相的电压、电流信号被进行3-2变换为α-β坐标系下的二维数据。电压信号Uαβ的时间序列是网络的输入,电流信号Iαβ的时间序列是输出。为了验证工作点变化对模型有效性的影响,变换器的参考功率指令P*,Q*也被包含在输入信号中。当并网系统发生接地故障和参考功率指令发生变化时,记录Uαβ,Iαβ,P*,Q*的时间序列作为训练样本和测试样本。时间序列数据可以通过PMU、录波器等设备进行采集。值得注意的一点是,高采样频率下的样本数据可以建立更短时间尺度的模型,但同时会增加训练负担。因此需要在选择建模精度和训练成本上进行折衷。
3.2 网络结构设计要点
对于神经网络来说,神经元的权重W和偏置b是网络的参数,需要通过模型训练更新得到确定。神经网络的层数、每一层的神经元类型、每一层神经元个数都需要在网络训练以前提前确定,也是网络结构设计的要点。
在进行网络结构设计以前,需要对被建模的电力变换器的复杂程度进行估计。网络中GRU单元的数量应该超过电力变换器内的系统状态数。然而,过多的GRU神经元会造成较大的计算负担,造成训练过程漫长。GRU神经元数量过少会造成最终训练得到的模型精度不够。为了获得更好的非线性特性拟合效果,FC层中应该包含足够的常规神经元。此外,为了提升神经网络训练速度,需要在网络输入端加入归一化层。具体的结构参数设计,需要根据实际情况进行估计,会在后文通过仿真算例展示。
3.3 网络训练
在进行网络训练以前,需要先确定评价训练效果的指标,即目标函数。由于输入数据是时间序列,所建立的神经网络与真实的输出时间序列之间的均方根误差(root-mean-square error,RMSE)作为目标函数。RMSE的计算公式为

式中:yi为端口电流在i时刻的瞬时值;oi为神经网络在i时刻的计算值;N为一条训练样本的时间序列长度。
此外,优化器的选择也是网络训练中需要考虑的环节。基于作者以往的经验,本文选择Adam优化器进行网络训练,优化器的学习率通常可以设置为0.01。
4 仿真算例及分析
为了验证本文所提算法的有效性,在此开展仿真实验。暂态过程数据在Matlab/Simulink软件下进行仿真模拟得到。在TensorFlow下根据仿真数据,对所提出的神经网络进行训练,并验证模型精度。仿真系统结构如图4所示,一台电力变换器与短路电流比为1的电网相连,电力变换器的控制拓扑如图1所示。为了模拟使用PMU进行数据采集,这里将接入点的电压、电流采样频率设置为2 000 Hz。

图4 仿真系统结构Fig.4 The structure of simulation system
用于训练网络模型的数据通过Simulink下的多次不同暂态仿真获得。一部分是由外部三相接地短路故障引起的变换器接入点暂态过程获得。随机选取1~40 Ω范围内的30个接地电阻作为不同接地短路故障情况,其中20个作为训练样本,10个作为测试样本。另一部分是由变换器的P*,Q*变化引起的接入点暂态过程获得。P*,Q*在0~5 kW范围内随机选取30个样本,其中20个作为训练样本,10个作为测试样本。
根据对被建模电力变换器所包含状态数量的估计,对本文提出的网络模型进行结构设计,如图5所示。网络的前两层由GRU神经元组成,后两层由传统的神经元组成全连接神经网络层。基于训练数据集,所提出的网络模型所包含的全部权重W和偏置b经过模型训练后确定。训练过程的迭代周期设置为1.1万次。训练过程中,目标函数的衰减过程如图6所示,最终目标函数的RMSE衰减至约0.3,可以认为模型训练结果能够满足精度要求。利用测试样本集对训练完成的网络模型进行验证,对应的目标函数RMSE为0.4,验证了所建立模型的精度。
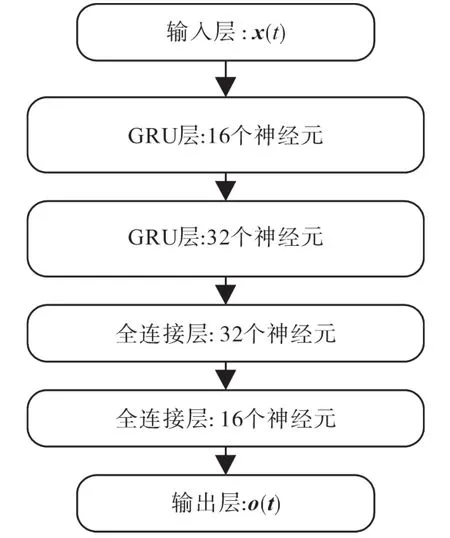
图5 所建立神经网络结构Fig.5 The structure of the proposed neural network

图6 训练过程目标函数曲线Fig.6 The curve of cost function in training procedure
图7为变换器接入点在接地电阻为2 Ω的接地短路故障下的暂态过程,短路时长为0.1 s。观察有功功率和iα暂态过程可以发现,提出网络模型的输出能够准确拟合仿真过程测量得到的数据波形。图8为变换器接入点在接地电阻为8 Ω的接地短路故障下的暂态过程。可以看出,尽管短路接地电阻发生了变化,但所提出的模型能够准确拟合测量数据,模型的准确性不受接地电阻影响。

图7 2 Ω接地短路故障下暂态过程Fig.7 Transient behavior under 2 Ω short-circuit fault
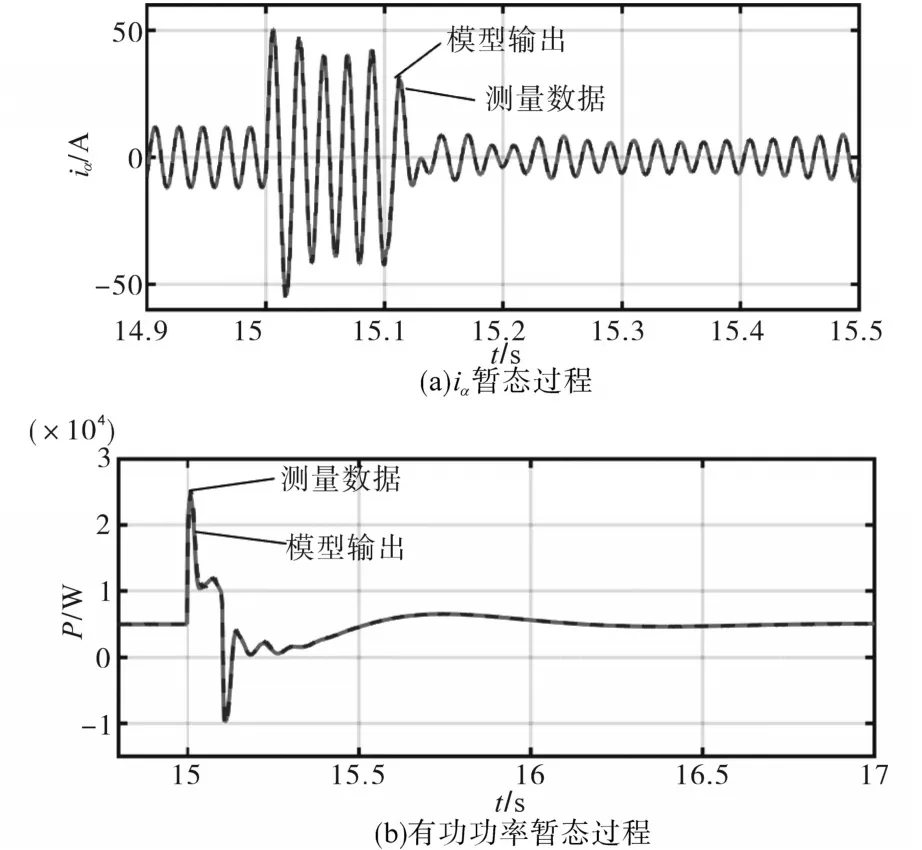
图8 8 Ω接地短路故障下暂态过程Fig.8 Transient behavior under 8 Ω short-circuit fault
当改变电力变换器的参考功率P*时,变换器接入点的暂态过程如图9所示。P*于15 s时由3 kW跳变至4 kW,引发了有功功率的暂态过程如图9b所示,同时引发了无功功率的暂态过程如图9c所示。可以看出,所提出的模型能够准确拟合仿真测量数据。端口的电流暂态过程(如图9a所示)也能够得到准确拟合。仿真结果说明本方法在改变参考功率指令下都能够准确拟合测量数据,验证了本方法在宽范围多个工作点下模型的有效性。
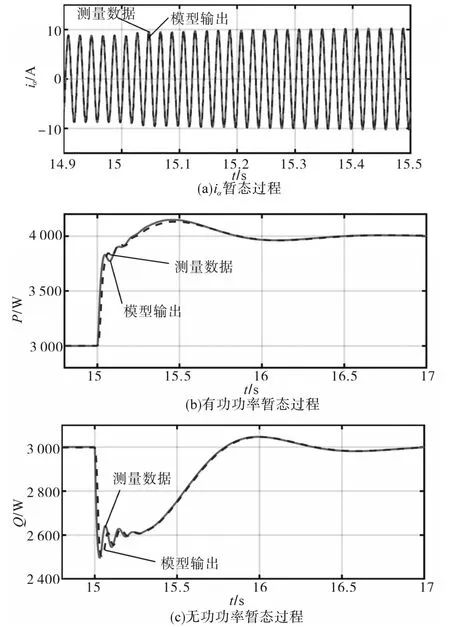
图9 参考有功变化时端口暂态过程Fig.9 Transient behavior under P*changed
5 结论
文中提出了一种基于深度学习方法的电力变换器宽范围暂态等值建模方法,该方法以建立黑盒非线性微分代数方程组为核心思想,采用基于GRU的深度神经网络的方法,进行变换器暂态建模,克服了以往黑盒线性建模方法只在单一工作点有效的缺陷。
仿真结果表明所提出的方法能够在大扰动下实现精确建模,并且在宽范围内多工作点均有效,适用于解决控制拓扑及参数未知的电力变换器暂态等效建模问题。
