电动汽车用开关磁阻电机集成功率变换器设计

孙丽华，张琳，孙会琴，郭英军，李争，郭天亮

（河北科技大学电气工程学院，河北 石家庄 050000）

开关磁阻电机（switched reluctance motor，SRM）由于其稳定性高，适合在恶劣环境中工作等优势成为最具潜力的车用电动机。传统电动汽车-开关磁阻电机系统有两个电能分配装置，分别是由整流器、功率因数校正（power factor correction，PFC）电路组成的充电装置，和用于电动机驱动的功率变换器。性能优越的功率变换器具有快速励磁和退磁功能，控制元件数量少、集成度高，同时各相绕组相互独立，具有良好的稳定性和容错能力的特点。

目前有很多文献研究了不同的功率变换器拓扑结构。文献[1]提出的一种在不对称半桥前端加入额外的DC-DC变换器的拓扑结构可以实现灵活充电，但是增加的电感和电容元件降低了功率密度，增加了电路的复杂程度。文献[2]提出的具有电池充电功能的公共开关式功率变换器拓扑提高了集成度，但由于各相共用一个开关管，各相绕组无法独立工作，容错性能差。文献[3]提出的新型变换器将电源系统和驱动系统融为一体，并且通过升压斩波电路提升了系统的性能，但Boost电路的动态响应很难满足电机在高速时的要求。文献[4]提出的用于电动汽车的被动升压式变换器提高了输出转矩和系统的效率，但额外的电容电感降低了系统的功率密度和容错能力。文献[5]提出的四电平的结构有效地解决了电流拖尾导致的负转矩，特别适合电机的高速运行，而固定的调制方法使得控制方法复杂。文献[6]提出的低成本的拓扑结构只能提高续流时的电压，但电路容错性能差，仅适合在工作环境好的场合。文献[7]提出的增加双倍功率开关管可以减小励磁电流的上升时间，虽然效果明显，但大大增加了系统的复杂程度。文献[8]提出的双电源的变换器不需要额外的硬件设备就可以实现电池的灵活充电，但双电源变换器难以运用在纯电动汽车上。文献[9]提出的低成本的变换器仅需要一个继电器就可以实现电机驱动和充电两种工作模式，却不能输出多电平以解决电流拖尾问题。文献[10]提出的用于电动汽车的拓扑结构增加了半无桥PFC电路，可以实现PFC充电功能，但增加的电气元件和开关管增加了系统的成本，并且电路没有输出多电平的能力。

本文提出了电动汽车用开关磁阻电机的集成式功率变换器（integrated power converter，IPC）。在不对称半桥式功率变换器的基础上增加前端电路，通过控制前端电路实现了电机驱动和电池充电的工作模式。在电机驱动模式下，IPC可以输出多电平，以解决电流拖尾的问题，并且利用电容器的充放电功能，提升系统的能量比、提高电能的利用率。在电池充电模式下，利用电路原有器件和电机绕组构建了整流电路和PFC电路，交流电网经过整流和功率因数校正后给电池充电，实现了在交流充电环境下的功率因数校正。将传统的电动汽车系统的充电装置和功率变换器融为了一体，提高系统的集成度。

1 传统的SRM功率变换器

1.1 不对称半桥式功率变换器

开关磁阻电机不对称半桥式功率变换器各相绕组相互独立，具有良好的稳定性和容错能力[11]，其拓扑结构如图1所示。每相绕组有两只主开关和两只续流二极管，有三种工作状态，以A相为例说明。

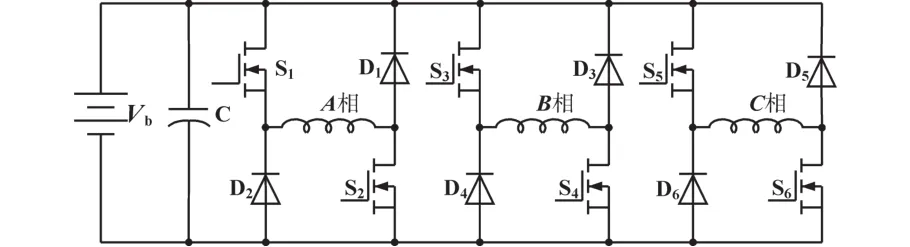
图1 传统不对称半桥式功率变换器Fig.1 Traditional asymmetric half bridge power converter

工作状态1：励磁状态，开关管S1和S2导通，电流通过S1和S2给A相绕组励磁，绕组相电流上升。

工作状态2：零电压续流状态，开关管S1截止，S2导通，A相绕组电流经过S2和D2闭合，绕组两端电压为零，由于反电势的存在，使得电流缓慢下降。

工作状态3：续流状态，开关管S1和S2截止，电机绕组中的磁场储能以电能的形式通过D1和D2迅速回馈电源，实线强迫换相，A相绕组电流快速下降。

1.2 开关磁阻电机的数学模型

忽略开关管压降，绕组k电压平衡方程如下式所示[11]：

式中：Uk为绕组的相电压；Rk为绕组的等效电阻；ik为绕组的相电流；Ψ为绕组的磁链；“+”为励磁阶段；“-”为续流阶段。

电磁转矩方程如下式所示：

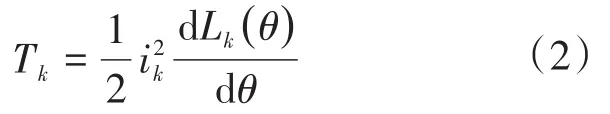
式中：Lk为绕组电感；θ为转子位置角。

转子运动方程如下式所示：

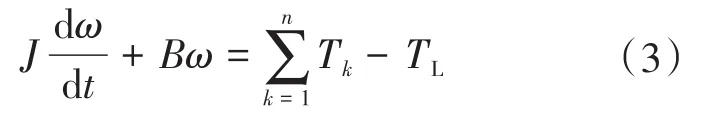
式中：J为转动惯量；ω为转子的转速；B为摩擦系数；n为电机的相数；TL为负载转矩。

2 集成式功率变换器的设计

2.1 集成式功率变换器的拓扑结构

电动汽车正常运行时，电池的电能被IPC分配给电机的各相绕组。当电动汽车驻车充电时，IPC将电能进行整流和功率因数校正，最后给电池充电。基于IPC的电动汽车系统能量流图如图2所示。

图2 基于IPC的电动汽车系统能量流图Fig.2 Energy flow diagram of electric vehicle system based on IPC

IPC的拓扑结构如图3所示，前端电路由继电器J1和J2、开关管S01和S02及电容器C2组成。电动汽车正常行驶时，IPC工作在电机驱动模式，拓扑结构如图3a所示，此时，继电器J1连接到M点，J2导通，续流二极管 D1，D3和 D5与电容器 C2相连。电动汽车驻车充电时，继电器J1连接到C点、J2断开，开关管S1一直处于导通状态，S01和S02处于截止状态，利用开关管S3和S5的反并联二极管D7和D8与续流二极管D4和D6组成不可控整流电路；利用A相绕组、开关管S2和二极管D1组成升压式PFC电路。IPC工作在充电模式，拓扑结构如图3b所示。

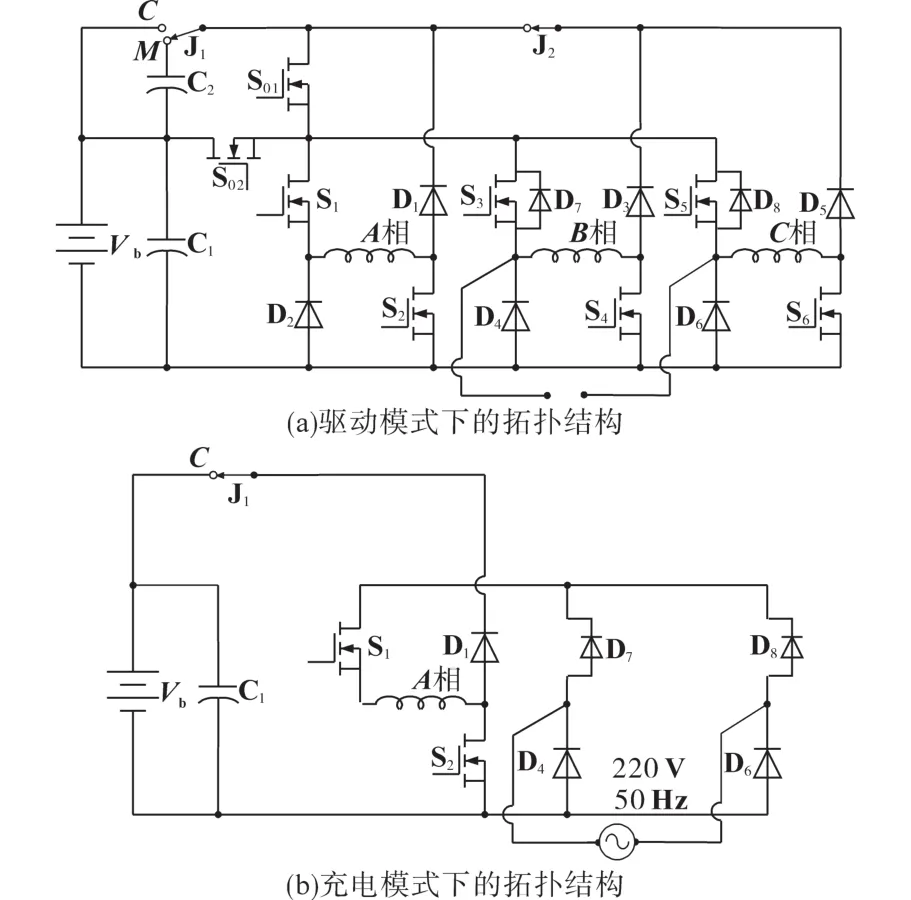
图3 IPC在不同模式下的拓扑结构Fig.3 The topology of IPC in different modes

2.2 驱动模式分析

2.2.1 电压特性

传统的功率变换器在电机低速时有良好的性能，在高速运行时，由于反电势的影响，绕组的相电流延伸到了电感下降区[12]，由式（2）可以知道，电感对角度的微分为负时会产生制动转矩，如图4中实线所示。

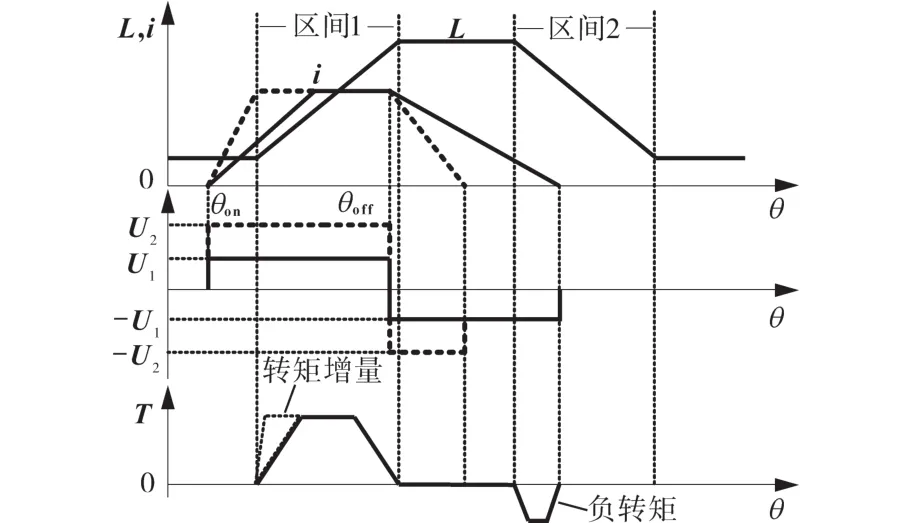
图4 不同电压下的电动机情况Fig.4 Motor conditions at different voltages

为了解决上述会产生制动转矩的问题，对式（1）进一步分析可以得到下式：

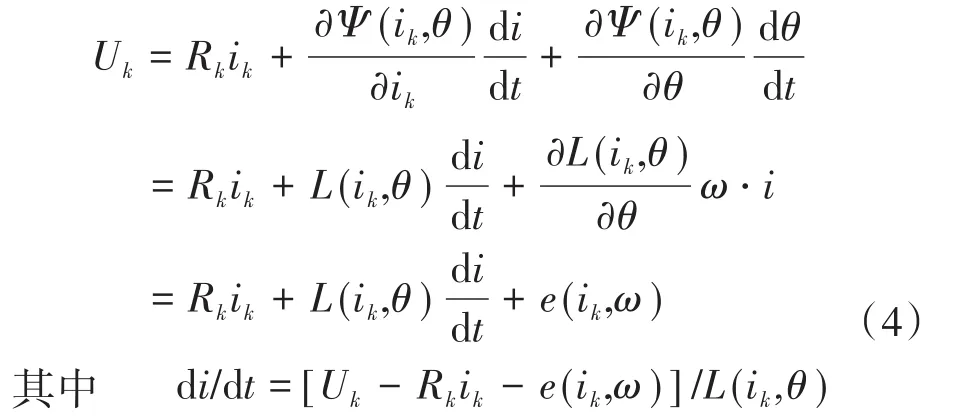
由式（4）可知，电流变化率与电压幅值成正比。如果将电压的幅值从U1提高到U2，励磁时，电流快速上升，从而增加了输出转矩；退磁时，电流快速下降，可以消除制动转矩，达到图4中虚线所示效果。

2.2.2 电感非线性化

为进一步准确描述电机换相的过程，将线性电感波形进行傅里叶展开，并取其中的平均分量和基波分量可以得到下式[13]：

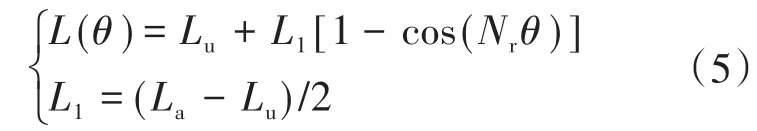
式中：Lu为最小电感值；La为最大电感值；Nr为转子极数。

图5为非线性绕组电感、相电流和M点电位的波形。

图5 绕组的电感、电流和M点电位的波形Fig.5 Waveforms of inductance，current and potentials of M point

2.2.3 工作方式分析

IPC的工作过程中包括励磁方式、零电压续流方式、快速励磁方式和快速退磁方式。

在图5区间0～θ1内，A相绕组单独导通，采用电流斩波控制限制电流，当电流小于最小波动电流 Δimin时 S01截止，S02，S1和 S2导通，电路工作在励磁模式增大电流，电流流向如图6a所示；电流大于Δimax时仅有S2导通，电路工作在零电压续流的方式减小电流，电流流向如图6b所示，此方式维持恒定的转矩。区间θ1～θ3为换相区间，在区间θ1～θ2内，S1，S2和 S02截止，S3，S4和S01导通，A相绕组退磁，B相绕组励磁，此时A相绕组产生很高的感生电势，一方面给电容C1和C2充电，另一方面给B相绕组建立磁场，电容器C2抬升了M点电位，此时A相绕组电流快速下降，而B相绕组的电流快速上升，进入快速励磁模式，电流流向如图6c所示；在区间θ2～θ3内，虽然各开关状态不变，但A相绕组的感生电势下降至UC1+UC2，电容器C2开始放电，此时由A相绕组、电容器C1和C2共同给B相绕组供电，M点电位开始下降，A相绕组电流快速下降，B相绕组电流快速上升，进入快速退磁模式，电流流向如图6d所示。转子到θ3之后，电容器放电完毕，使开关管S01截止，M点电位回到UC1，B相开始电流斩波控制。

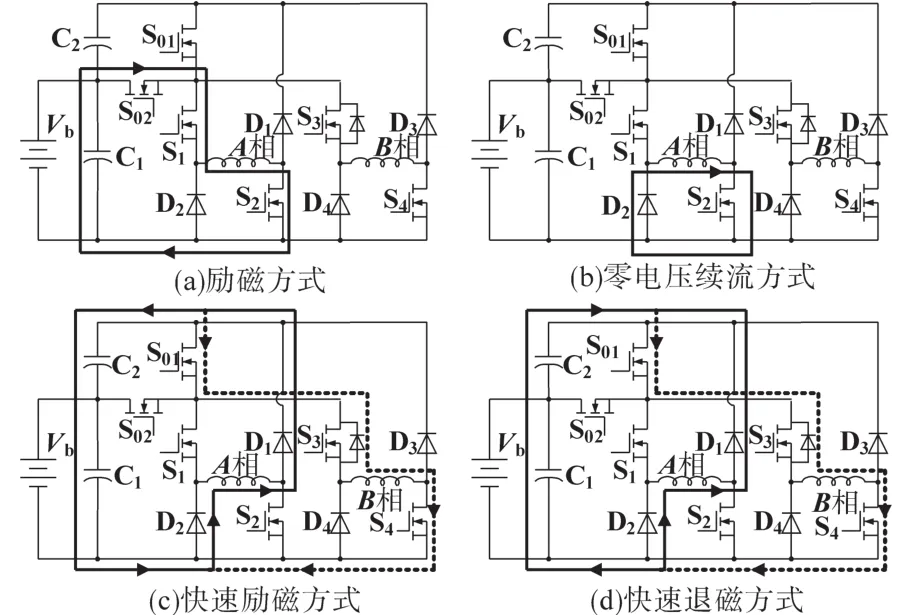
图6 驱动模式下不同的工作方式Fig.6 Different working states in driving mode

2.3 电容器容量设计

2.3.1 系统能量比

通过对电路工作过程的分析可知，电容C2储存了一部分来自绕组反馈的电能，并将该电能利用到下一相的励磁过程中[14]，电机驱动系统下输入能量如下式所示：

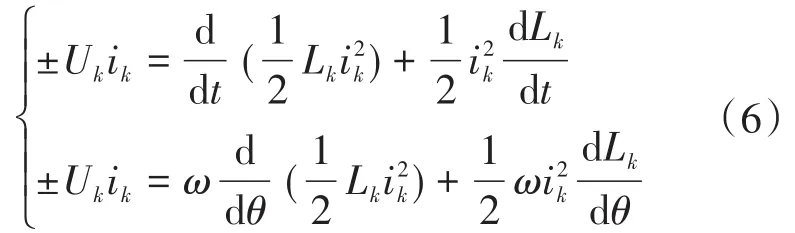
式中：“+”表示励磁时从电源向绕组输入的电能；“-”表示续流时绕组向电源反馈的电能。

励磁时，单位时间内电源向电机绕组输入的电能一部分以磁能的形式储存在绕组()，另一部分转换为机械能()。续流时，绕组储能会反馈给电源。

由于开关磁阻电机驱动系统使用非正弦交流电，提出“能量比”的概念代替功率因数，反映电能利用率，定义能量比EM如下式所示：

式中：P为输出的有功功率；X为输入的总电能。

由于电容器C2的储能作用，减少了反馈回电源的电能，提高了系统的能量比，同时储存于电容器的电能提高了母线电压、提升了电机的转矩输出能力。

2.3.2 电容器参数估算

电容器C2的容量直接影响驱动系统性能，容量选择过大会导致电压上升速度变慢，使得母线电压的增量变小。容量过小的电容器的耐压值往往不能满足需求。

忽略绕组的内阻，根据图6d所示电流路径可以得到电压方程：

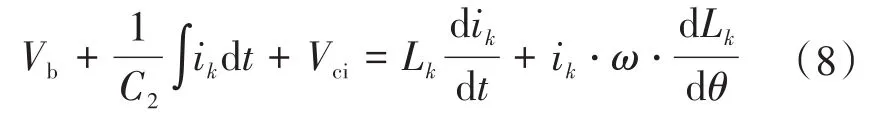
式中：ik为绕组相电流；Vci为电容初始电压。

假设初始电流为Io，忽略反电势项的影响，相电流表达式可以由下式解出：

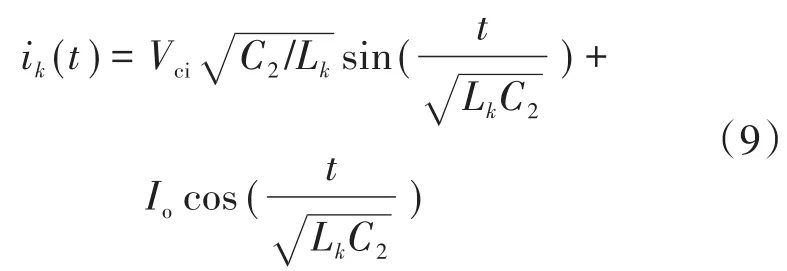
电容C2的电压纹波值计算公式如下：

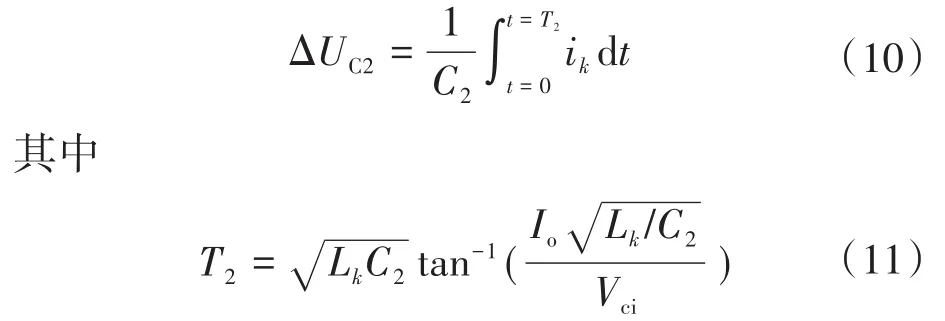
式中：T2为电容C2充电时间。

将式（9）、式（11）代入式（10），可得电容电压的纹波值如下式所示：

限定纹波值的大小，可得电容器C2的估算公式如下式所示：

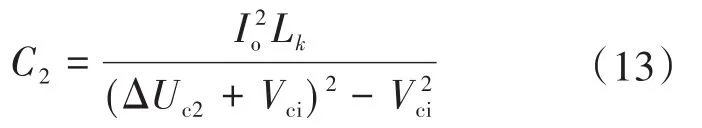
2.4 充电模式分析

当电动汽车驻车充电时，IPC可以实现PFC充电功能。图7为图3b的等效电路，开关管S1一直处于导通状态，当S2导通时，电流通过整流电路转换为直流电，接着给A相绕组励磁。当S2关断时，整流电路和A相绕组共同给电池充电。以网侧电压的相位信号为反馈，通过控制开关管S2，使A相绕组电流跟随网侧电压的相位，间接地使网侧电压和电流同相位，从而可以有效地增大功率因数。通过对S2进行PWM控制可以实现功率因数校正功能。

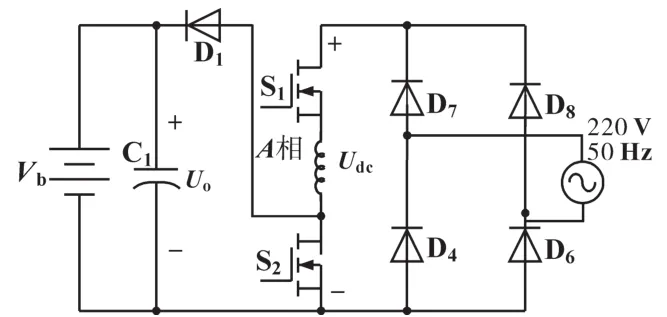
图7 充电模式下的等效电路Fig.7 Equivalent circuit in charging mode

2.5 绕组复用的限定条件

SRM的绕组作为PFC电路中的电感使用时，需要满足升压电路的使用条件，根据文献[15]可以得到下式：

式中：Lmin为充电所需最小电感量；Udc为整流电路输出电压；Uo为PFC电路输出电压；ILM为电感电流最大值；fs为开关管工作频率。

当电机绕组作为存储电感使用时，该A相绕组凸极会吸引转子凸极与之对齐，使得所利用相绕组电感值LA最大，限定条件可以写为LA≥Lmin。另外，充电时流过绕组的电流有效值不能超过电机运行时的额定电流，否则会烧坏绕组。

参考文献[15]的电流有效值计算公式，可以得到充电时二极管D1、开关管S2和A相绕组上电流有效值ID，IS和IL的计算公式[3]为

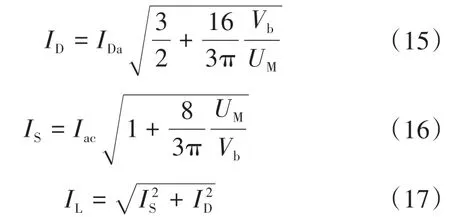
式中：Vb为电池电压；UM为交流电压峰值；IDa为通过二极管电流的平均值；Iac为输入的电流的有效值。

3 系统的仿真与分析

3.1 仿真系统组成

IPC的控制系统如图8所示，驱动模式的控制采用电流和转速的双闭环结构，转速的误差信号δω经过PI控制器得到参考电流i*，与电流反馈信号相减后得到电流误差信号δi，经过滞环控制器得到所需占空比，根据开关角生成驱动信号S1～S6。另外，为了防止电容器C2被反向充电，需要在电压降低到阈值以下时使S01截止，在右侧的虚线框中给出了开关管S01的开关逻辑。

图8 IPC的控制系统框图Fig.8 IPC control system block diagram

电动汽车充电分为两个阶段，第一阶段进行30 A恒流充电，PFC电路输出电压会逐渐上升，当电压达到250 V时进行第二阶段的充电，即恒压充电。将升压电路输出电压与给定电压的差作为比例积分控制器的输入，其输出的i＇A与交流电压相乘，获得与交流电压同相位的绕组参考电流，经过比例积分控制生成调制信号，与载波比较后生成对S2的PWM信号。载波为双极性的锯齿波，改变锯齿波的周期可以改变PWM的频率。

3.2 仿真系统参数

SRM在额定电压下运行，并搭载额定负载（运行电流为额定电流），仿真系统中参数如下：电机定转子极数12/8，绕组电阻0.05 Ω，最大电感值2.2 mH，最小电感值0.67 mH，额定功率30 kW，额定电压250 V，额定电流100 A。

仿真系统充电模式主要计算参数：1）电池恒流充电时，绕组上的平均电流接近50 A，PFC输出的平均电流为30 A，即Ioa=30 A；2）电池标称电压为200 V，满负荷电压为250 V，恒压充电时的给定电压250 V，即Uo=250 V；3）充电电压Uac为220 V/50 Hz，峰值电压311 V，交流侧电流有效值Iac为45.45 A；4）PFC电路工作在CCM模式，并且开关管的工作频率fs=20 kHz；5）电容器C2估算容量约为75 μF左右；6）充电时二极管D1的电流方均根值ID为71 A，开关管S2的电流方均根值IS为34 A、电感上经过电流的方均根值IL为79 A，低于电机的额定电流。电感电流最大值为111 A；7）充电所需最小电感量Lmin为0.093 mH，对齐位置的电感量远远大于所需的电感最小量，满足绕组复用的限定条件。

基于上述计算参数，选取耐压300 V，额定电流110 A，最大开关频率 25 kHz，MOSFET型号HM3307，反向耐压250 V，正向电流80 A，肖特基二极管型号MBR60100PT。

3.3 驱动模式下仿真结果分析

3.3.1 电容器容量与能量比

仿真测试了估算值C2为75 μF左右不同容量对系统的影响。

表1给出了负载为100 N·m，给定转速为5 000 r/min情况下，电容器容量对母线电压、可达到的最高转速和最高能量比的影响（容量0代表不对称半桥式功率变换器）。C2容量为10 μF时，母线的峰值电压接近600 V，而一般电解电容的耐压值小于500 V。容量为50 μF时，最高转速约达到4 800 r/min，母线电压最高达到488 V。C2容量为75 μF时，母线电压提升不大，转速的提升不明显。IPC与不对称半桥功率变换器相比，有效地提升了能量比。综合分析后，C2的容量选取50 μF。

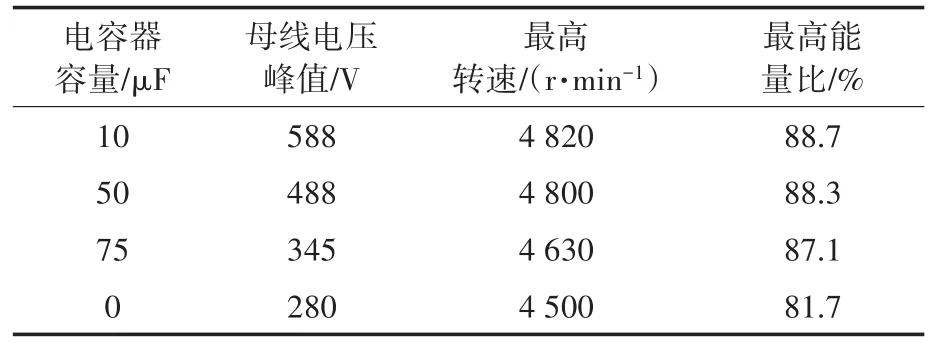
表1 C2不同容量对系统性能的影响Tab.1 Influence of C2capacity on system performance

3.3.2 驱动模式下仿真结果

图9给出了C2为50 μF时电机的A相电压、三相电流和合成转矩的波形图，可以看到每段高电压的作用时，对应相电流变化速度增快。而在一个周期内，高电压作用时间小于该周期的10%，所以器件的电压应力并不高。

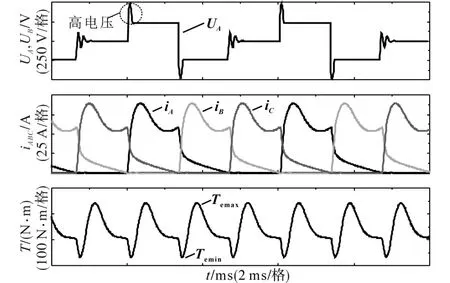
图9 电机A相电压、三相电流和合成转矩的波形Fig.9 waveforms of A phase voltage，three phase current and resultant torque of motor

3.4 充电模式下仿真结果分析

3.4.1 电感电流仿真结果

恒压充电时，如果在电压信号误差的绝对值为0.1时，给定的电感电流平均值为50 A，则可以得到比例系数P的估计值为500，通过工程试凑法，比例系数最终整定值为524。当开关频率为20 kHz，比例系数P为524时，图10为充电时电感上电流波形，图11上下2子图分别给出了经过PFC处理前后的电网侧电压、电流波形，交流侧电流的总谐波失真（THD）约为11%，功率因数为0.96。处理前功率因数低，形成损耗。处理后有效地实现功率因数校正的功能。

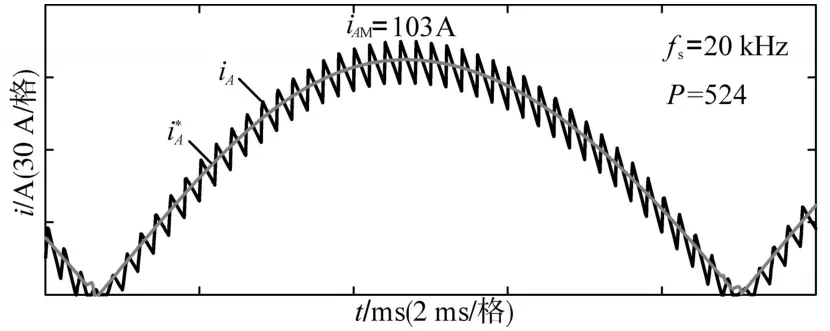
图10 开关频率为20 kHz时的给定和实际的电感电流波形Fig.10 Given and actual inductance current waveforms at 20 kHz

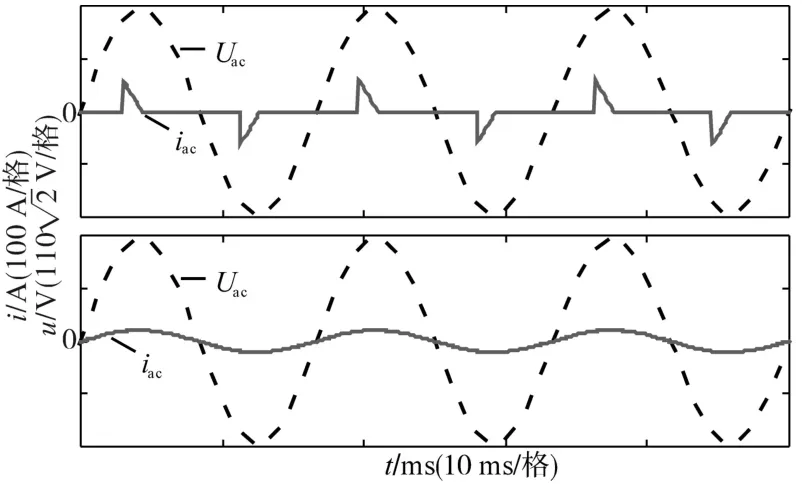
图11 PFC处理前后交流侧电压和电流波形的对比图Fig.11 Comparison of voltage and current waveforms at AC side without PFC and with PFC

3.4.2 电池充电仿真结果

图12为电池的荷电状态、PFC电路的输出电压和充电电流的波形图，在阶段1时，充电电流的平均值维持在30 A左右，PFC电路的输出电压逐渐升高，当电压高于预设值时进入阶段2充电，此时输出电压恒定在250 V左右，电流逐渐降低，当电流为零时表示电池已经充满。

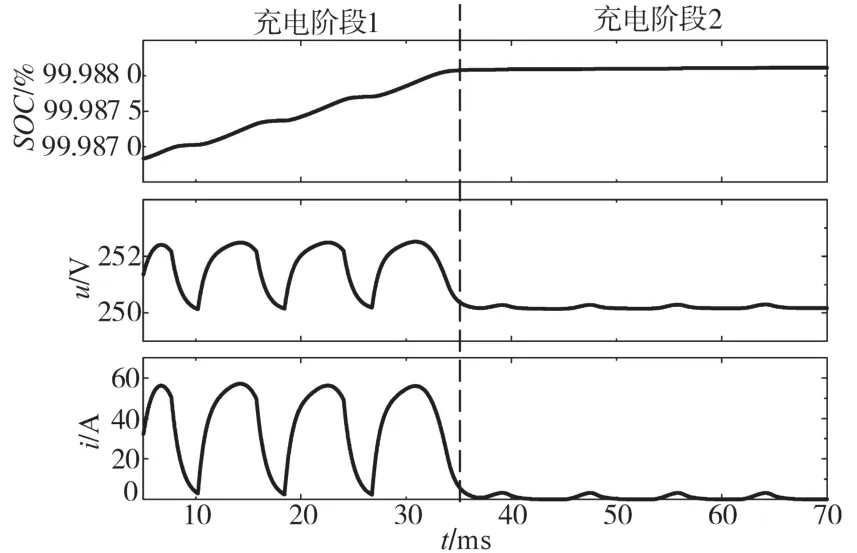
图12 充电阶段转换时电池荷电状态、PFC电路输出电压和充电电流的波形图Fig.12 Waveforms of battery state of charge，PFC circuit output voltage and charging current during charging stage transition

4 结论

本文提出了一种新型的集成功率变换器（IPC），同时具有电机驱动和充电两种模式。给出驱动模式下的不同工作方式，分析了电容容量对母线电压、转速和最高能量比的影响；研究了充电模式中绕组复用的限定条件，实现了具有功率因数校正的充电的功能，有效地提高了系统的功率因数。最后测试了电池的充电响应，结果表明该变换器可以实现先恒流再恒压的充电方式。仿真结果说明IPC在电机驱动和充电时均提高了电源的利用率。