基于流固耦合的大功率IGBT模块散热结构设计
2022-05-05高凤良黄雄峰范虹兴张炫焜
高凤良,黄雄峰 ,范虹兴,张炫焜
(1.三峡大学电气与新能源学院,湖北 宜昌 443002;2.合肥工业大学电气与自动化工程学院,安徽 合肥 230009;3.国网金华供电公司,浙江 金华 321017;4.国网重庆市电力公司党校(培训中心),重庆 400053)
绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)同时具有高输入阻抗和低导通压降的特点[1-2],在功率半导体器件中具有很高的商业价值。近年来,IGBT模块在各个领域应用广泛,如电动汽车、舰船、高速火车、智能电网、风力发电机和高压直流输电等[3-4]。当IGBT模块在高频工况下作业时,产生的功率损耗增大,尤其当设备电压等级较高、功率较大时(MV·A级),会造成更高的温升,研究表明,由于温度引起功率器件的失效占将近六成[5]。在器件处于温度较高的工况下,长期运行过程中将要承受温度和应力的波动,会对其寿命等造成影响,为保证器件能够安全稳定的运行,对设备的散热系统也提出了更高的要求,水冷的散热能力是强制风冷的15~30倍[6],与传统的强制风冷相比,水冷散热更具优势。因此,对IGBT模块进行流场-温度场耦合计算,研究IGBT功率模块的散热机理,可以为IGBT模块散热结构的优化提供理论依据,对提高模块工作时的安全性和可靠性具有重要意义。
目前,国内外学者对大功率IGBT模块的散热问题做了一些研究。如在电动汽车中,IGBT模块主要的散热方式为液冷散热,已被证明散热效果较为明显[7];通过对散热器散热结构进行改进,增大传热面积,使流体尽可能多的带走热量,可以提高散热效率[8-9];用有限元仿真软件分别对顺排针柱散热器和叉排针柱散热器进行数值模拟分析,结果表明叉排针柱散热器对流体具有很好的扰流作用,散热效果比顺排针柱散热器好[10];通过对微通道进行建模,设计不同形状的翅片,研究翅片形状和排列间距对散热效果的影响,结果表明三角形散热器的翅片散热效果最好[11]。以上文献从不同角度对散热器的结构进行设计来改善散热器散热性能,但对IGBT模块流场-温度场数值计算方法研究较少。
本文通过对IGBT模块水冷散热进行理论分析,提出基于流场-温度场耦合的温升计算方法,并利用有限元仿真软件对IGBT模块进行流场-温度场耦合计算;之后搭建温升试验平台测量模块的结温,对比分析仿真结果与实验结果;最后改进散热器结构,分析不同结构下的散热效率,为散热器结构的优化设计提供依据。
1 温升计算方法
1.1 功率损耗计算方法
正常工作条件下,IGBT模块的结温主要来自内部芯片功率损耗所产生的热量,因此,要对IGBT模块进行流场-温度场的耦合分析,需要准确地计算模块在运行过程中产生的功率损耗。
IGBT模块开关频率较高时,在开通、关断过程中会产生能量损耗,称为动态功耗;在导通、关断状态下产生的功耗称为静态功耗[12]。IGBT模块关断状态下,几乎无电流流过,模块的关态功耗为零。因此,IGBT模块的总功率损耗P主要由通态功耗Pf和开关功耗Ps组成。通态功耗Pf为

式中:Uon为模块开通时的导通压降;Ion为流经器件的电流。
开关功耗Ps与IGBT模块开通和关断过程中电流、电压的大小有关,同时也受开通和关断所用时间的影响[13],其开、关功耗分别为
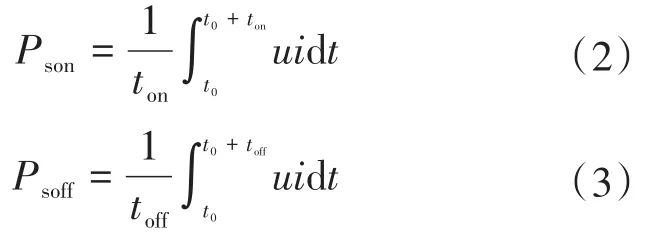
式中:Pson为开通功耗;Psoff为关断功耗;u,i分别为模块开关过程中瞬时电压值和瞬时电流值;t0为初始时间;ton,toff分别为开通、关断过程中所用时间。所以:
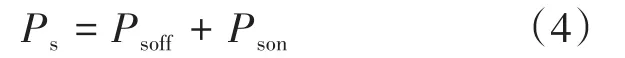
1.2 基于流场-温度场耦合的温升计算方法
1.2.1 热传递理论
热传递有热传导、热对流和热辐射3种传递方式[14]。在实际运行过程中,IGBT模块热传递同时包含以上3种方式,但在对IGBT模块进行热分析时可以忽略比较弱的热传递现象[15]。
热传导是固体之间热量传递的主要方式,IGBT模块在运行过程中,芯片内部会产生大量的焦耳热,热量自上而下形成传导通路,依次经过上焊料层、上铜层、覆铜陶瓷基板(direct bonding copper,DBC)、下铜层、下焊料层和基板。对流传热是以流体为介质,利用流体可流动性和热胀冷缩的特性传递热量。为使IGBT模块工作时结温处于安全范围内,通常会在模块基板下方安装散热器,来增强模块和流体之间的热量传递,降低模块的整体温度。采用强制对流能够加快对流传热,使散热效果更加明显。一般情况下,IGBT模块的极限工作温度通常为150℃。研究表明,当物体温度超过500℃时,辐射传热才比较明显,因此,在正常工况下IGBT模块产生的热辐射效应可以忽略[16]。本文采用有限元数值模拟的方法分析含散热结构的IGBT模块温度场分布情况,根据以上热传导理论,含散热结构IGBT模块的稳态温度场方程可以表示为

式中:λ为导热系数;x,y,z为坐标轴方向;qv为热源密度;α为对流散热系数;为沿边界法向的温度变化率;T为材料温度;Tf为流体温度。
1.2.2 流体控制方程
不同流动状态下的流体对应不同的控制方程,对冷却液流动状态的判定是进行水冷基板仿真模拟的第一步,冷却液流动状态判定依据为雷诺数(Re)的大小,雷诺数的定义为

式中:ρ为冷却液密度;u为入口流速;d为水流直径;μ为冷却液的动力黏度。
本文IGBT模块水冷散热器冷却液采用纯 水,其密度为 996.52 kg·m-3,动力黏度为0.000 895 kg·(m·s)-1,水冷散热器的进水口直径为0.01 m,进水口流速为1 m·s-1;水导热系数为0.59 W·(m·K)-1,比热容为4 186 J·(kg·K)-1。根据式(6)可以计算得到雷诺数Re=11 134,可以判定水冷基板内水的流动状态为湍流。
IGBT模块水冷系统中,冷却水的流动控制方程可表示如下。
1)冷却水的质量守恒方程。冷却水的质量守恒方程可以表示为

式中:ux,uy,uz为水在x,y,z方向上速度矢量u的分量。
2)冷却水的动量守恒方程。冷却水的动量守恒方程可以表示为

式中:t为时间;p为水微元体上的压力。
3)流体湍流方程。文中设定冷却水为不可压缩流体,标准k-ε模型方程可以表示为

式中:t为时间;k为湍流动能;ε为耗散率;μt为水的湍动粘度;xi,xj为坐标位置;i,j为下标,i,j=x,y,z且i≠j;Gk为层流速度梯度产生的湍流动能;σk,σε为普朗特数;C1ε,C2ε为常量;u,v,w分别为x,y,z方向的速度分量。
2 IGBT模块建模及求解
2.1 IGBT模块封装结构
基于不同的封装工艺,IGBT模块主要分为焊接式和压接式两大类。焊接式IGBT封装结构如图1所示,由下到上,IGBT内部结构依次为散热器、基板、下焊料层、DBC层(下铜层、陶瓷衬板、上铜层)、上焊料层、芯片、键合线,IGBT芯片和续流二极管(freewheeling diode,FWD)芯片通过键合线利用超声焊接技术连接在一起;器件内部与外壳之间的缝隙填充硅胶,可以缓解外部震动对内部器件的影响;对底板进行特殊加工设计,使底板与散热器表面结构高度吻合,减小接触面间隙,提高模块的散热能力。
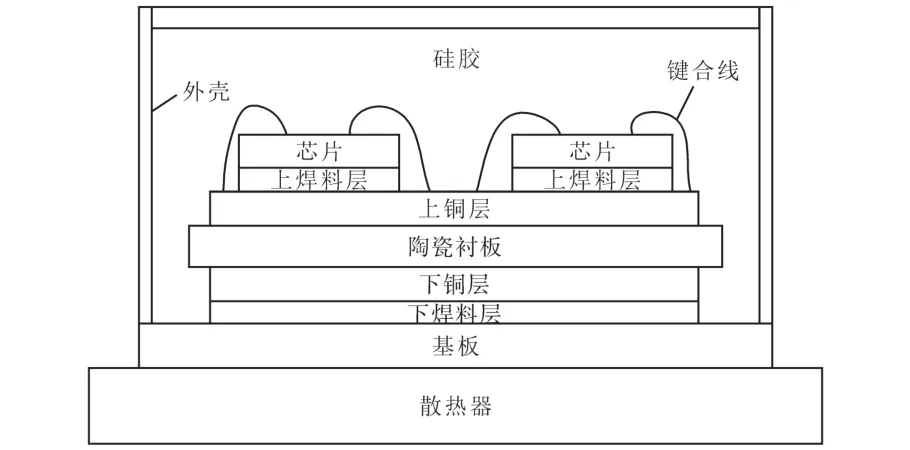
图1 焊接式IGBT模块封装结构图Fig.1 Structure diagram of welded IGBT module
2.2 含散热结构的IGBT模块的有限元模型
文中选取型号为5SNA 0800N330100焊接式IGBT模块为研究原型,其额定电压为3.3 kV,额定电流为800 A。IGBT模块内部分2个管,每个管由2个单元并联而成,单元内部包含4片IGBT芯片和2片FWD芯片,芯片下方通过焊料与上铜层焊接在一起;下铜层焊接在基板上,基板与芯片之间通过DBC陶瓷层绝缘隔离。
IGBT模块为型号5SNA 0800N330100,水冷散热器为400 mm×300 mm×40 mm的长方体结构,根据实际尺寸建立其等比例几何模型,IGBT模块仿真模型如图2所示,散热器结构如图3所示。

图2 IGBT模块仿真模型Fig.2 Simulation model of IGBT module

图3 水冷散热器结构图Fig.3 Structure diagram of water-cooling radiator
考虑仿真计算复杂程度,对几何模型进行简化。键合线对功率模块温度分布影响较小[17],因此在建立有限元模型时可将其忽略。IGBT芯片为整个模块的热源,热量经焊料层向下传递,在划分网格时,对芯片层、焊料层进行精细网格划分,对其他部分采用标准划分尺寸。
由焊接式IGBT封装结构图可知,模块各层由不同的材料封装而成,通过查阅相关资料来确定各层材料属性,如表1所示。温度对硅材料的导热系数、热容的影响较明显,在数值模拟计算时需要考虑因温度变化而引起的材料属性的变化(具体函数关系见表1)。

表1 IGBT各层材料属性Tab.1 Material properties of each layer of IGBT
2.3 IGBT模块边界条件
温度场边界条件:在仿真计算时,把芯片作为热源,直接在芯片上加载功率损耗模拟芯片的发热。当器件处于长期导通状态时,模块总功率损耗将由IGBT芯片的通态损耗组成,通过功率损耗计算公式,计算出平均功率损耗为3.08 kW;环境温度取25℃,散热器表面与空气之间的对流换热系数为5 W·(m2·℃)-1。
流场边界条件:假设散热器中冷却水为连续不可压缩液体,其性质为恒值,冷却水与散热器管道接触边界各处的流速均为零,出口边界条件指定为充分发展流动,进水口水温为25℃,水流速度设置为1 m·s-1。
3 仿真结果分析
对含散热结构IGBT模块的流场温度场的耦合计算后,经有限元分析软件后处理,可以得到含散热结构的IGBT模块各部分温度场分布的情况,求得的最终结果如图4~图6所示。

图4 含散热结构的IGBT模块整体温度分布Fig.4 Temperature distribution of IGBT module with heat dissipation structure

图5 水冷散热器温度分布Fig.5 Temperature distribution of water-cooling radiator

图6 散热器流体温度分布Fig.6 Temperature distribution of fluid in radiator
由图4可知,IGBT芯片作为热源,热量从上往下、从中间向四周扩散传播;芯片的最高温度为129.18℃,小于IGBT工作的极限温度。
由图5可知,热源主要集中在中间区域,热量向周围扩散,中间区域温度最高为84.6℃。
由图6可知,随着水的流动,水温会逐渐升高,但流向出口时会略微降低,在热源附近达到最高为43.9℃,出水口温度为40.1℃。
4 IGBT模块温升试验
搭建的IGBT温升测试平台基本构成如图7所示,主要包括电源系统、水冷系统、温度系数测试系统、监测与控制系统和数据采集系统等。监测与控制系统可以结合下位机来实现各个系统间的通信和控制,以实现温度数据的自动采集,同时还能保证测试设备稳定可靠的运行。

图7 IGBT模块温升测试平台基本构成Fig.7 Basic composition of IGBT module temperature rise test platform
由于IGBT芯片封装在模块内部,直接测量其结温难以实现。经研究发现,当给IGBT模块通入小电流时,其饱和压降与结温表现出一定的规律,两者之间呈线性关系[18],关系图如图8所示。因此,温升测试中结温的测量可采用小电流下饱和压降法进行推导[19]。
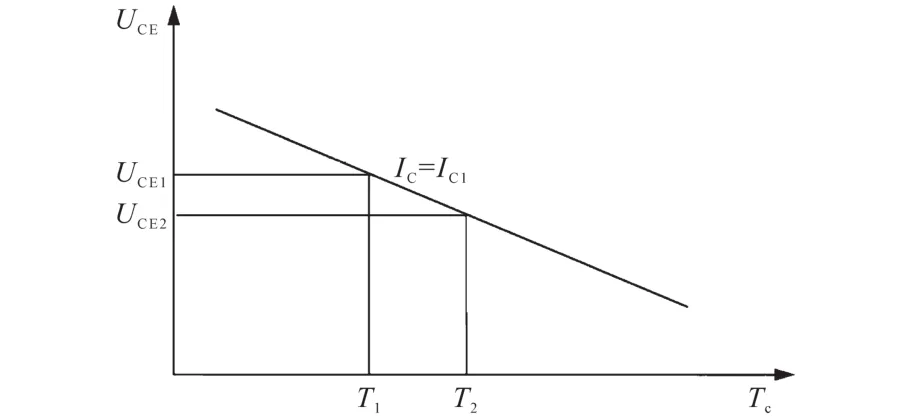
图8 小电流测量下IGBT导通压降与结温关系图Fig.8 Relationship between IGBT turn-on voltage drop and temperature under low current measurement
在进行温度系数测试时,随机选择两个IGBT模块放入恒温箱内,测量电流取100 mA,测试温度从30~150℃每隔20℃,保持45分钟,测量不同结温、小电流下的UCE的值,得出结温与UCE两者的关系式。经过多次测量取平均值,计算后温度系数为-2.28 mV/℃,结温压降关系式截距为0.512 79。
计算出结温与导通压降关系式之后,将IGBT模块安装在温升测试系统中的试验工位上,如图9所示,并在上位机中设置试验参数,具体数值为:加热时间30 s,冷却时间30 s,测试电流100 mA,环境温度25℃,温度系数-2.28 mV/℃,UGE=15 V。然后开始温升测试。
实验时,选取室温下的纯水为冷却介质,在两种不同的工况下进行温升测试实验。工况①:不同电流梯度下IGBT模块温度测试。实验时加载电流设定范围为100~800 A,电流变化梯度为100 A;进水口流速为1 m/s,水温为25℃。工况②:不同进水口流速下IGBT模块温度测试。实验时设定电流为800 A,进水口流速的范围为1~2 m/s,进水口流速变化梯度为0.2 m/s,水温为25℃。以上实验中,每组数据测试10次取平均值。
5 仿真与实验对比分析
IGBT模块温度测试实验结果与仿真计算结果对比如图10和图11所示。由图10可以看出,随着电流的增大,仿真温度和实验温度的差值越来越大,但不同电流下的IGBT模块实验结温与仿真结温的误差为5%左右,属于正常误差范围,实验结温与仿真结温相比较高;由图11可以看出,不同进水口流速下的IGBT模块实验结温与仿真结温的误差为4%左右,且进水口流速越大,IGBT模块结温越低,散热器散热效果更明显。

图10 不同电流梯度下IGBT模块温度Fig.10 IGBT module temperature under different current gradients

图11 不同进水口流速IGBT模块温度Fig.11 IGBT module temperature under different water inlet flow rate
6 散热器结构优化设计
散热器管道结构的不同将会直接影响流体在管道内的流动状态,会改变流体流速的大小和速度场分布,进而对散热器的散热效果产生影响。因此,对管道结构进行优化设计可以提高散热效率。在保证管道截面积不变的条件下,将圆形管道结构设计成长方形结构并对整个模块进行流场-温度场耦合计算,从结果中读取IGBT模块的最高结温为125.77℃,虽小于圆形结构的129.18℃,但效果提升并不明显。因此,进一步对长方形管道做了两种不同结构的优化设计,一种是把管道截面由长方形改成凹凸形;另一种是在管道两侧增加扰流挡板,优化后的管道结构如图12所示。在对散热器管道结构优化设计的过程中,为了能够准确地分析不同管道结构对IGBT模块温度场分布的影响,需要保持管道结构的长度和截面积不变。设计完成后,基于不同的管道结构对整个IGBT模块进行耦合场数值计算,其他条件不改变,得出不同进水口流速下IGBT模块最高结温如图13所示。
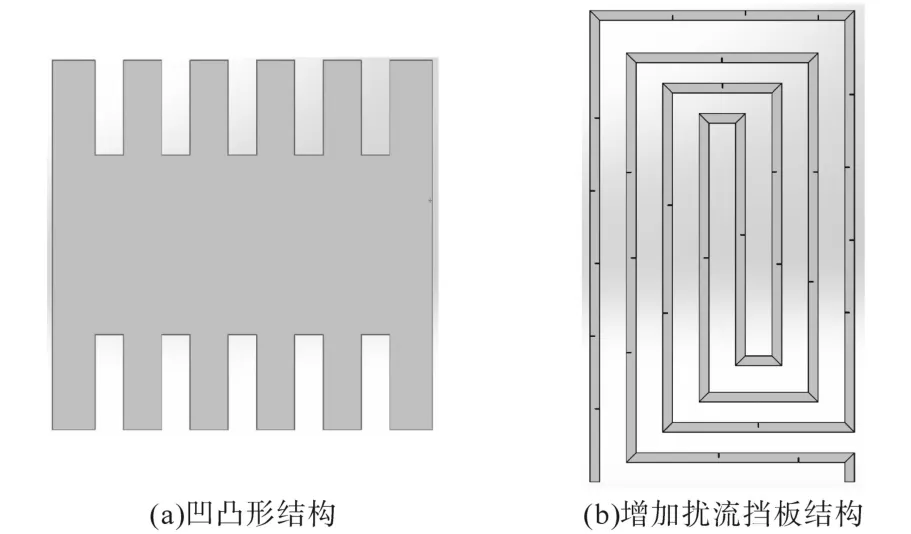
图12 优化设计后的管道结构Fig.12 Optimized design of pipeline structure

图13 各管道结构不同进水口流速IGBT模块温度Fig.13 The temperature of the IGBT module with different inlet flow rate for each pipeline structure
由图13可以看出,在进水口流速为1 m/s时,凹凸形结构和扰流结构下IGBT模块的最高结温分别为118.46℃和121.48℃,说明经过优化设计后的散热器散热效率提升明显;随着进水口流速的增加,IGBT模块的最高结温会随之降低,但当流速大于3.5 m/s时,散热效果提升并不明显,考虑实际使用成本,最佳进水口流速应在3.5 m/s左右。
7 结论
通过对含散热结构IGBT模块的流场温度场的耦合计算和温升测试,可以得出以下结论:
1)采用有限元仿真软件对含散热结构的IGBT模块进行数值计算,仿真结果能够直观体现流体流动的情况和温度分布情况,可以为散热器结构的优化设计提供理论依据。
2)基于耦合场数值计算的结果能够说明流体可以带走大功率电子器件工作时产生的热量,让器件工作时的结温处于允许范围内。采用水冷散热器能够提高器件的可靠性和安全性,且进水口流速越大,散热效果愈加明显。
3)由仿真结果和实验结果对比分析可知,温度变化基本一致,其误差在正常范围内,验证了理论分析和仿真计算的正确性。
4)水冷散热器主要是通过对流换热来实现对大功率电子器件的散热,换热面的传热面积和形状以及流体介质和流动情况是影响对流换热的主要因素。因此,在优化设计散热器结构时可以考虑增大传热面积、改进换热面形状和增强扰流强度,如散热管道可以采用叉排结构来增强散热效果。
