基于模糊神经网络的燃煤锅炉炉膛结渣特性研究

朱 超，郁 翔，李 峰，周熙宏，毕凌峰，杨 冬

(1.国网陕西省电力公司电力科学研究院，陕西 西安 710100；2.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049)

0 引 言

当前，我国电力行业仍以煤炭为主要能源消耗，加之电站锅炉常用燃煤中的硫含量与灰分较高，易造成受热面的积灰和结渣，而炉膛严重结渣将限制锅炉出力，威胁机组运行的经济性与安全性[1-3]。锅炉炉膛结渣是一个不断加剧过程，一旦发生结渣，炉内水冷壁的吸热减少，导致水冷壁外壁温与灰渣温度升高，加上灰渣表面不平滑，灰渣更易发生黏附，加剧结渣过程[4]。炉膛结渣包含一系列错综复杂的物理及化学反应，不仅涉及煤灰的结渣特性，还受到煤燃烧、炉内传热传质及管壁与灰渣静电吸附等因素影响[5]。我国常用的判断燃煤结渣特性的指标较多[6]，主要考虑灰分熔点和影响灰熔融温度的灰分成分，也开发出许多研究煤灰结渣特性的特殊方法，但存在很大局限性。单一结渣判别指标分辨率较低，综合判别指标并未充分考虑主要影响因素。因此，开发一种全面、综合性的结渣预测模型将是进一步研究重点，可对锅炉炉膛结渣程度进行有效监测[7-9]。杨冬等[6]依据煤灰渣组分工业分析，建立了综合指标判据与单一指标判据的超临界锅炉结渣趋势预判程序，该模型虽然运算速度快、结构简单，但预测准确率偏低，且无法预测锅炉燃用煤种不均匀时炉内情况。王宏武[10]采用不同的聚类算法预处理燃煤电站锅炉结渣指标，通过支持向量机算法(SVM)预测炉膛结渣趋势，该方法在选择不同的聚类算法和聚类指标时，预测结果变化较大，若想获得较高的预测精确度，则需进行多个分类计算，计算量较大。任林等[11]提出一种优化量子粒子群(QPSO)算法，建立了优化量子粒子群算法改进隶属函数的模糊SVM燃煤电站锅炉结渣倾向预判模型，通过与试验结果对比，该模型准确度较好，但单一优化改进量子粒子群算法具有较大局限性。

判定锅炉炉膛的结渣特性可被视为典型的模式识别问题，而神经网络的一个重要功能是模式识别技术[11]。在上述研究基础上，笔者将模糊数学理论和神经网络相结合，采用4种不同类型的隶属函数，将判别指标模糊化后，作为模型输入，并将不进行模糊化处理的神经网络作为对比，根据统计学原理，选用出现概率最大的结果作为最终指标，构造了炉膛结渣的模糊神经网络模型，以此判定华能秦岭电厂660 MW超临界锅炉常用混煤的结渣特性，为综合评价锅炉炉膛的结渣特性提供了新方法。

1 模糊神经网络的拓扑结构

1.1 BP神经网络算法

神经网络算法不仅具有自我学习功能，能快速找到最优解，还有很强的泛化能力和一定的容错能力，最显著特点在于超强的非线性映射能力[12-13]。BP算法即多层前馈网的误差反向传播算法(Back Propagation)，在神经网络中的应用极为广泛，其核心思想是将每一个神经元的均方根误差当作目标函数，依据不同训练算法优化修正阈值与权值，将全局误差调整到最小[14]。运算过程由2部分组成：输入样本的前向计算与误差的逆向散布，其结构如图1所示，初始运算循环中，由已知的样本输入数据，结合初始化的阈值与权值计算各隐层和输出层神经元的输入和输出，根据神经元的实际输出和期望输出得到目标函数，依据不同训练函数对阈值与权值求偏导来获得修正值，依照输出层—隐层—输入层的顺序逆向修正参数，网络反复迭代计算，当达到设置的循环次数或要求的精度时，结束循环。

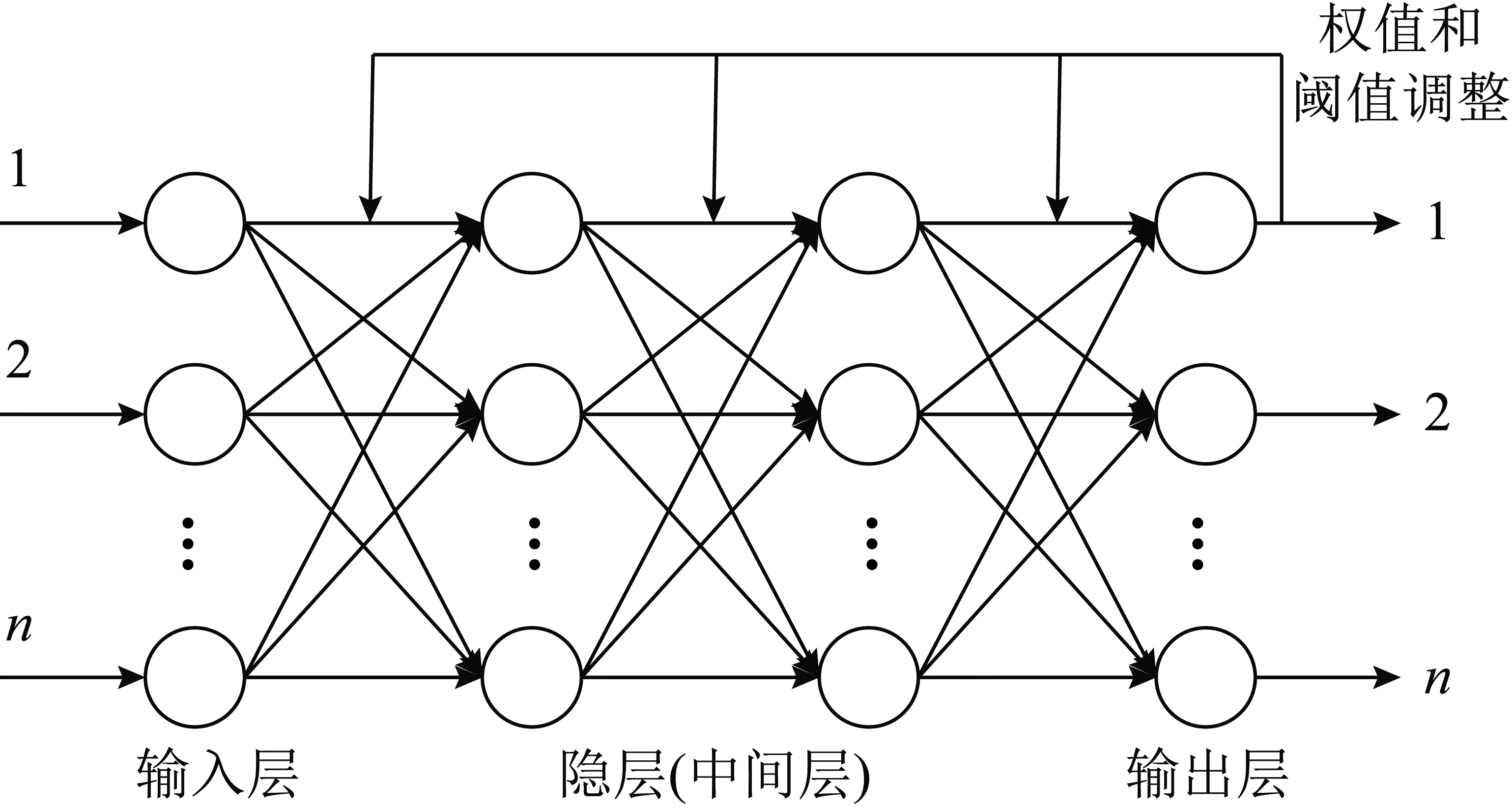
图1 BP神经网络的组成结构Fig.1 Composition structure of BP neural network

BP神经网络网络的前向计算：

(1)

式中，yj为对应神经元的输出值；m为迭代计算次数；j为层数；f为传递函数；n为神经元总个数；i为神经元序数；wij为权值；xi为对应神经元的输入值；θj为阈值。

误差的反向传播过程：

均方误差E：

(2)

式中，Ri为对应xi的期望输出向量。

(3)

(4)

其中，Δw为对应步长下权值的变化量；η为动量梯度下降算法中的步长，也称学习算子或收敛因子(0<η<1)；Δθ为对应步长下阈值的变化量。

BP神经网络是一种有监督式的学习算法，其使用分为2个过程：① 学习过程，根据输入的学习样本，不断调整输入层与隐层、隐层与输出层间的权值和阈值，使输入与输出间建立特定的非线性映射关系，只有建立科学、有效的学习网络才能利用此网络实现后续计算预测。神经网络学习过程如图2所示。② 计算过程，输入计算样本，利用上述建好的各层间权值、阈值对样本进行计算，得到预测结果。可以看出神经网络预测结果的精确度取决于学习网络输入、输出的准确性及广泛性，因此需保证学习样本尽可能准确和全面。

1.2 模糊逻辑与神经网络的结合

炉膛结渣是一个模糊化的概念，结渣程度是一个由轻变重的历程，笔者应用“模糊化”概念，将模糊数学理论与BP神经网络算法串联型结合，使用模糊数学理论，采用4种不同类型的隶属度函数将判别结渣程度的6个指标模糊化后作为模型的输入，以3种不同的炉膛结渣程度，“轻微”、“中等”与“严重”作为模型的输出，构成模糊神经网络模型，再根据上述BP算法进行训练，最终可以用于预判锅炉炉膛的结渣特性。

2 炉膛结渣模糊神经网络模型

2.1 输入判别指标的确定

造成锅炉炉膛结渣的主要原因不仅包括煤灰自身因素，还包括锅炉炉膛结构、运行参数2类外部因素[15]。目前我国判别结渣的指标较多，各指标在对应的适用范围内具有一定精度[16]，仅靠单一指标很难准确预测结渣特性，其中硅比R(Si)和软化温度t2准确度最高[17]。另外选择代表煤灰成分特性的指标如碱酸比R(B/A)、硅铝比R(Si/Al)以及准确度最高的综合指标R作为炉膛结渣的判别指标。此外，考虑到锅炉运行方式对炉膛结渣特性影响，引入炉膛无因次最高温度ψt，确定了6个评价指标，各指标表达式[17]具体为

(5)

φ(Fe2O3)=1.43w(Fe)+1.11w(FeO)+w(Fe2O3)，

(6)

R(B/A)=

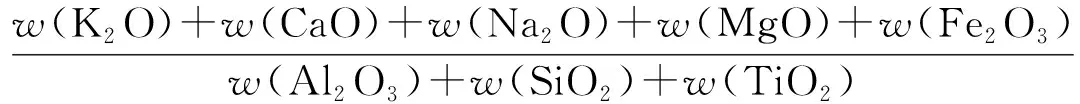
(7)

R=5.41-0.002t2+1.24R(B/A)-0.02R(Si)+

0.28R(Si/Al)，

(8)

(9)

(10)

其中，w为质量分数；φ为当量；a、b分别为炉膛宽度、深度，m；Bj为计算燃料消耗量，kg/s；Qd为煤的低位发热量，kJ/kg；ηf为二次风层数；ξ为卫燃带修正系数；Ca为二次风距，m；Fw为卫燃带面积，m2；h为燃烧器高度，m。不同判别指标的结渣评价标准见表1。

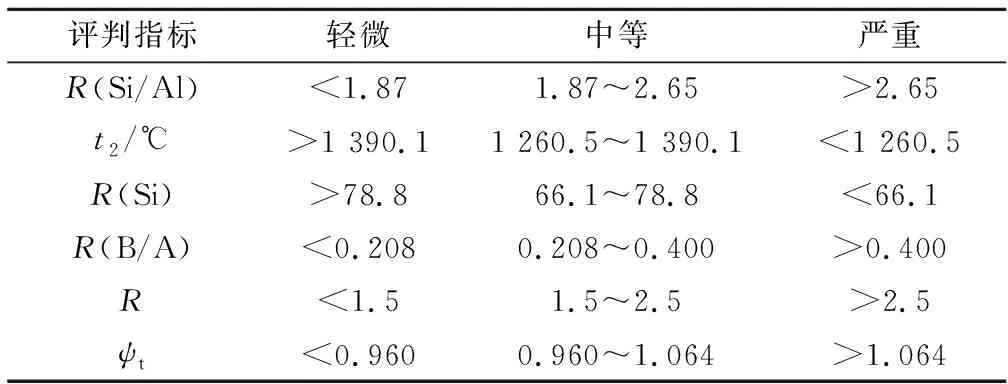
表1 不同判别指标的评价标准Table 1 Evaluation criteria of discriminant indexes

2.2 输入判别指标的模糊化

通常将锅炉炉膛结渣情况划分为“轻微”、“中等”、“严重”3种程度。由于结渣程度难以量化，不同结渣程度之间没有明确的界限，因此引入每一个指标的隶属度函数将其模糊化处理，求得指标相应的不同结渣程度的隶属度。利用隶属度函数将输入判别指标模糊化，得到模糊集合，作为神经网络模型的输入。采用不同隶属度函数对输入数据进行处理，得到不同的模糊集合，作为神经网络计算数据初始值计算时会得到不同结果，分别利用4种隶属函数对每一输入项进行了模糊化处理：三角形(Trimf)、梯形(Trapmf)、高斯形(Gaussmf)以及π形(Pimf)，另设一传统神经网络(No-fuzzy)即不进行模糊化处理的神经网路与上述4种模糊化处理后的网络进行比较，4种隶属函数的数学模型如图3所示。

图3 隶属函数数学模型Fig.3 Mathematicalmodel of membership function

以硅比R(Si)为例，分别写出了三角形隶属函数对应不同结渣程度的表达式。其他判别指标函数形式相似，构造各种类型的隶属度函数，求得不同判别指标的隶属度。

(11)

(12)

(13)

其中，r1、r2、r3分别为“轻微”、“中等”、“严重”的隶属度。输入层经模糊化处理后作为网络结构的第1隐层，因此第1隐层共3×6=18个节点。

2.3 第二隐层与输出层的确定

输出层设置3个神经元，分别对应于样本结渣程度，“轻微”、“中度”、“严重”。由于输出层与隐层间的传递函数采用了S型传递函数，因而输出层各神经元的输出值只能趋向于但不能等于1和0。规定“轻微”、“中度”与“严重”3种结渣程度分别对应的输出为(0.99，0.01，0.01)、(0.01，0.99，0.01)、(0.01，0.01，0.99)。所建立的模糊神经网络拓扑结构以Trimf形为例如图4所示。

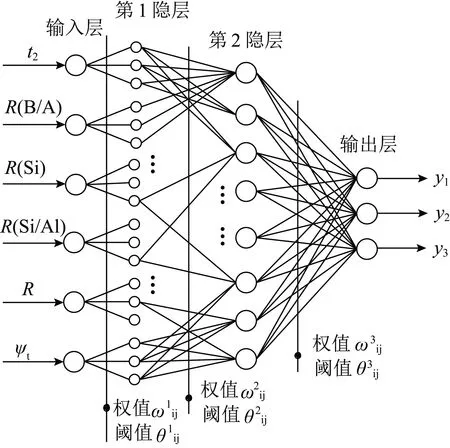
图4 模糊神经网络拓扑结构Fig.4 Topology of fuzzy neural network

在MATLAB神经网络工具箱中的训练函数有:附加动量法(Traingdm)、自适应学习速率法、共轭梯度法、RPROP方法、拟牛顿法以及Levenberg-Marquardt方法(Trainlm)[19]。使用MATLAB神经网络工具箱对建立的模型进行训练和计算，与C/C++、FORTRAN等语言相比，MATLAB的功能更加强大，且语法规则简单。

2.4 各层节点传递函数

传递函数包含3种：Purelin型、Logsig型以及Tansig型。3种传递函数的表达式如下：

fp(x)=x，

(14)

(15)

(16)

传递函数曲线如图5所示。

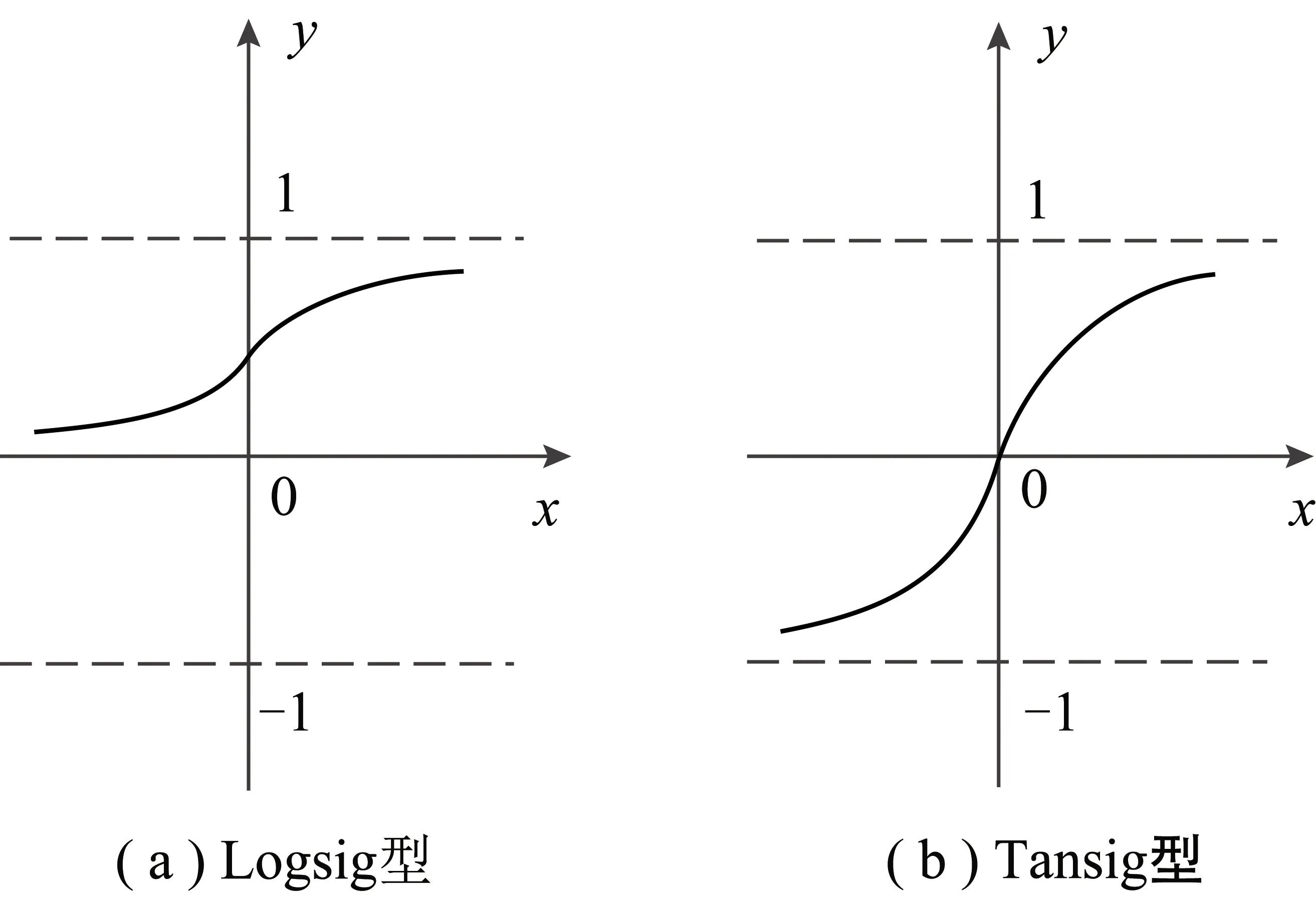
图5 传递函数曲线Fig.5 Transfer function graph

输入层经模糊化处理后通过Purelin型传递函数线性传递给第1隐层，根据隶属函数性质可知此时第1隐层值域为(0，1)，为确保输出层值域的广泛性，第2隐层和输出层间传递函数选用Logsig型传递函数，输出层值域同样为(0，1)。

2.5 训练函数和学习函数

训练函数的功能在于全局调整神经网络的阈值与权值，现有函数10多种，由于构建的神经网络较为简单，学习样本较小，选用Trainlm训练函数。Trainlm训练函数适用于中等规模的神经网络，具有学习速度与收敛速度快等特点。

学习函数是对训练函数的进一步补充，用于局部调整阈值和权值。训练函数计算得到阈值和权值后，由学习函数重新调整阈值和权值进行，再由训练函数进行训练，不断重复。选用带动量的梯度下降的权值和阈值学习函数(Learngdm)。

3 计算结果及分析

3.1 模型验证

在文献[18,20]中38组不同锅炉数据的基础上，利用28组作为神经网络学习数据，其他10组作为验证数据。分别用4种模糊神经网络和传统神经网络进行学习和预测。传统的神经网络直接将6项判别指标归一化处理后作为输入项，未进行模糊处理。表2和表3为验证集数据和不同神经网络的预测结果。

续表

表3 不同的神经网络预测结果Table 3 Different neural network prediction results

根据表3预测结果，传统BP神经网络的精度为70%，而4种模糊神经网络的预测结果更加精确，依次是80%、90%、90%和100%，由不同隶属度函数构造的模糊神经网络预测结果存在偏差。虽然π形隶属度函数构造的模糊神经网络预测精确度为100%，但由于预测样本较少，不能保证该模型对所有样本都能达到100%。因此，引入统计结果指标，并通过各种隶属度函数构造的模糊神经网络的计算结果来获得最终统计预测结果。与单一模糊神经网络相比，精确度大幅提高，只要确保学习过程选用的样本范围足够大，便可进行预测，且预测精确度高，对不同炉型和煤种的包容性更大。

3.2 实例计算分析

对华能秦岭电厂660 MW锅炉BMCR负荷运行时炉膛结渣情况进预测，分别对该机组常用华亭煤(煤种1)、黄陵1号煤(煤种2)、75%华亭煤和25%黄陵1号煤混配煤(煤种3)、50%华亭煤和50%黄陵1号煤混配煤(煤种4)以及、25%华亭煤和75%黄陵1号煤混配煤(煤种5)进行炉膛结渣预测，混配煤的煤质指标根据配煤煤质指标计算得到，表4为煤灰工业特性分析数据，表5为炉膛结渣判别指标计算结果。

表4 煤灰工业特性分析数据Table 4 Analysis data of coal ash industry characteristics

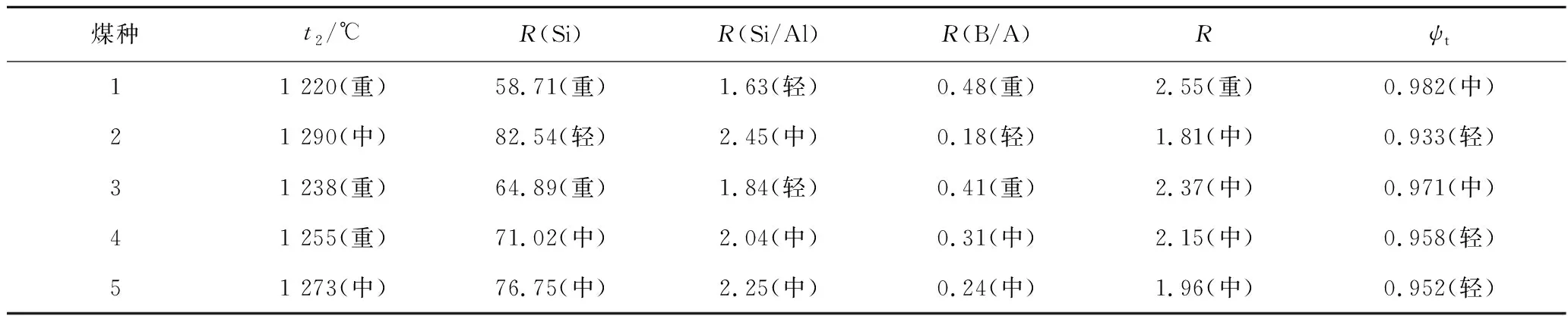
表5 炉膛结渣判别指标Table 5 Discriminant index of furnace slagging

根据表5计算结果，将该机组燃用不同煤种时的不同结渣判别指标值输入上述构建好的模糊神经网络进行预测计算，预测结果见表6。

表6 不同神经网络计算结果Table 6 Different neural network calculation results

由表6可知，单一燃用华亭煤时，所有神经网络模型预测结果均为严重结渣；燃用黄陵1号煤时，除No-fuzzy型神经网络预测结果为中等，其余均为轻微结渣，因此判断为轻微结渣；燃用掺烧25%黄陵1号煤的配煤时，Trimf型和Trapmf型神经网络预测结果为中等结渣，其余均为严重结渣，因此判断为严重结渣。燃用掺烧50%黄陵1号煤的配煤时，No-fuzzy型神经网络预测结果为轻微结渣，Trapmf型神经网络预测结果为严重，其余均为中等结渣，因此判断为中等结渣。燃用掺烧75%黄陵1号煤的配煤时，No-fuzzy型神经网络预测结果为轻微结渣，其余均为中等结渣，因此判断为中等结渣。综上所述，在单独燃烧华亭煤时，存在较严重的炉膛结渣问题，而适当掺烧黄陵1号煤时，炉膛结渣情况缓解。该方法预测结果准确，为综合评价锅炉炉膛的结渣特性提供了一个新途径。

4 结 论

1)在选择输入评判指标时，充分考虑了煤灰本身结渣特性和锅炉结构及运行工况的影响，选取了最具代表性、分辨率较高的几个因素作为本模型的判别指标，并将反映锅炉运行情况的结渣判别指标—无因次炉膛最高温度ψt纳入模型，将锅炉的运行工况考虑在内，判别依据更加全面。

2)将模糊数学理论与BP神经网络相结合，采用4种不同类型隶属函数，将判别指标模糊化后，作为模糊神经网络模型的输入，并将不进行模糊化处理的神经网络作为对比，根据统计学原理，选用出现概率最大的结果作为最终评判指标，增加预测结果的精确度。

3)采用构造好的适合于锅炉炉膛结渣的模糊神经网络模型对华能秦岭电厂660 MW超临界锅炉BMCR负荷运行时炉膛结渣情况进预测，结果表明该机组在燃用华亭煤时严重结渣，适当掺烧黄陵1号煤时中等结渣，因此可采用掺烧优质煤来改善炉膛结渣状况。该模型预测结果准确，为综合评价锅炉炉膛的结渣特性提供了新方法。