让“抽象”真实发生：数学抽象思想教学策略举隅

[摘   要]为说明抽象思想在数学教学活动中具体的思维活动以及现实表现，明确学生怎样才算是经历了抽象的过程，以及数学教师应如何加以引导，可以“沏茶问题”举隅。在教学时应将教学目标定位于“数学抽象思想的教与学”的层面，以培养学生数学思想素养为教学核心任务开展课堂教学，使学生经历“简化与命名、一一对应、比较与分类、次序化和序列化、数量刻画”等具体的抽象思维活动，通过对比、质疑、优化等探究活动，体验解决问题策略多样性，积累数学活动经验，培养数学学科核心素养，实现数学学习的意义。

[关键词]数学;抽象;有序思考;学科核心素养

“抽象”一词不仅经常会被数学研究者、教育者所使用，还经常出现在中小学教学研讨或教师教学设计中。但是“抽象”到底有哪些具体的思维活动以及现实表现，学生怎样的思维活动或探究行为才算是经历了抽象，教师又该如何引导并培育学生的抽象能力与素养呢？在此，笔者将结合“沏茶问题”的教学实践谈几点认识。

“沏茶问题”是人教版义务教育教科书小学数学四年级下册“数学广角——优化”单元的教学内容。教材呈现了沏茶的生活情境，具体工序及用时可概括为“烧水8分钟，洗水壶1分钟，洗茶杯2分钟，接水1分钟，找茶叶1分钟，沏茶1分钟”，所要解决的问题是“怎样尽快喝上茶”。教师引导学生确定沏茶工序、分析流程，继而交流和探讨怎样安排才能节省时间，从而体验解决问题策略的多样性和优化思想。但如果教师对这一内容的教学价值追求止步于此，则对作为数学思想专题教学的“数学广角”课程的定位缺乏充分的认识，对教材中蕴含的数学思想的挖掘也不够深入，而且也必然会因此而忽视了对学生数学学科核心素养的培育。笔者认为，“沏茶问题”中蕴含的最重要的数学思想应该是“抽象”。

一、“沏茶问题”中抽象思想的层次定位

抽象性是数学最本质的特征之一。“数学的威力就在于它的抽象性;越撇开内容，就越有广泛应用的可能。[1]”克莱因认为，数学从其抽象过程的特征来看，可以分为五种形式，包括理想化抽象、等置抽象、弱抽象、强抽象、无限抽象[2]。笔者认为，在中小学教学实践中，需要指向学生抽象思想形成的层次与类别的划分，要更为简明且利于引导学生由浅入深、由表及里地理解认识数学抽象思想。

1.数学抽象活动的类别

数学的研究对象从本质上来说都是经过抽象的东西。如果从抽象的“前后对象”的区别来看，笔者认为“抽象”活动可分为三类，即从物到数的抽象、从物到形的抽象、数与形的抽象。从物到数的抽象，其根本性在于，数是对物体数量这一本质的抽象，没有这一类的抽象，数学也就无从谈起了。在小学阶段，能够体现出“物—数”抽象并能转化为学生核心素养的有“数感、量感、符号意识”等基础能力;能够体现“物—形”抽象的能力素养包括“直观洞察、几何直观、空间意识”等;能够体现“数—形”抽象的能力素养包括“数据意识、数形结合、逻辑推理、模型与应用”等。“数—形”抽象包括“从数到形”，也包括数与数的自系统，形与形的自系统。

2.数学抽象活动的层次

史宁中教授指出，抽象可分为“简约阶段、符号阶段、普适阶段”三个层次。简约阶段是指，把握事物的本质，把复杂问题简单化、条理化，进行清晰简明的表达;符号化阶段是指，去掉具体内容，用概念、图形、符号关系表述简约的一类事物;普适阶段是指，通过假设和推理建立法则、模式或者模型，并能够在一般意义上解释具体事物[3]。受这种层次划分的启发，笔者认为，如果从“抽象”发生的复杂性和深刻性的角度分析，或可以包含五个层次：一是由客观现实世界到基本理性认识的抽象;二是由基本理性认识到一般数学理性认识的抽象;三是由一般数学理性认识到严密逻辑推理的抽象;四是由严密逻辑推理到模型化应用的抽象;五是由模型化应用到创新领域生成发展的抽象。

二、“沏茶问题”中抽象思想的具体体现

“沏茶问题”中的抽象思想关涉“物—数、数—形”抽象，主要是从物到数的抽象，而教师恰恰容易忽视这一抽象，仅仅对解决问题中的事物给予关注，缺少了从事物到数的进一步抽象刻画。从层次性来看，“沏茶问题”主要集中在第一、二层次的抽象，这也符合学生的相应认知能力。抽象体现在以下几个具体的阶梯式发展的抽象活动中，各环节环环相扣。

1.简化与命名

抽象经验不是凭空产生的，它必然建立在对客观事物的观察并产生直观经验的基础上，只不过在由直观表象转向抽象的准备阶段，还需要进行“抽丝剥茧”，这一过程就是“简化与命名”。“简化”是对纷繁复杂的信息进行分离和精简，摒弃那些与问题解决无关的或非主要关联的信息，保留关键信息。然后要对这些信息进行概括性的命名，以便以语言为载体进行思维，这是“抽象”运转起来的前提，也是抽象的具体表现之一，是抽象发生的较早期的行为。在“沏茶问题”中，要把“沏茶”这一具体的工作简化为六个工序，每个工序都给予简单的命名，就是在进行抽象的“准备”工作。鉴于此教学内容并不需要太多时间进行讲解，有些教师还会觉得内容“少了”，因此笔者建议不妨引導学生对“命名”进行符号化，比如“烧水——SS，洗水壶——XH，洗茶杯——XB，接水——JS，找茶叶——ZC，沏茶——QC”，在分析或设计流程时，以符号化的“命名”表达，既可以简化流程设计，亦可潜移默化地培养“符号化”的抽象意识。

2.一一对应

不同于集合运算中的“一一映射”，小学生应建立的“一一对应”意识是指能将观察到的客观事物与其抽象后的形式对应起来，从而开启初步的数学化思考。虽然这种思考显然不是高度综合的或系统化的，但却是开启理性认识大门的关键一环。皮亚杰就曾指出：“最基本的心理学观察揭示，一一对应是一种最原始的运算。[4]”在“沏茶问题”中，“一一对应”的发生多由学生思维意识的高度自动化完成，以致于常常被教师忽略。这里的“一一对应”表现在把沏茶的过程“分割”为一道道工序并与简化命名对应，并把每一道工序与其所用时间对应。有了一一对应，就构成了“数守恒”的前提，由此就可以做到无论各工序的顺序怎样变，工序的个数都不变。而且无论怎样调整顺序，只要是“一件接着一件的做”，那么所用的总时间就是相等的。“一一对应”对于学生思维认知结构的形成具有重要的、长远的作用，在教学中不能忽视。

3.比较与分类

“比较”是抽象过程中必不可少的一环，通过比较才能找出异同，才能认识共性，才有抽取共同性质后发现的本质特征，抽象也就因此而有了意义。在比较之后进行的区分其实就是“分类”。有学者认为“逻辑分组和分类是数学的核心组成部分”。分类也是集合思维的基础，集合又是最基本的数学结构之一。皮亚杰则认为“分类既为逻辑概念也为数学概念的发展提供了基础”[5]。“沏茶问题”中的各道工序大致可分为三类：一是关乎“水”，二是关乎“茶叶”，三是关乎“茶具”。对于学生来讲，看似简单的分类，其中已经包含了抽象与推理。皮亚杰指出：一个类不能由知觉构造而只能由逻辑构造，因为必须以一系列抽象和概括为前提，类的意义才从哲学抽象和概括中得出[6]。在此内容的教学中，“分类”的意义还在于对后续分析的铺垫，也就是说只有在分类的基础上才可讨论“沏茶问题”中的“同时做”这一“包含”范畴的思考。“沏茶问题”解决策略的关键就在于不同类的事物具有同时进行的可能，由此才有了做同样多的工序，总用时却减少了，从而實现了节省时间的要求。但与“对应”一样，教师很容易忽视“比较与分类”的教与学。事实上，很多儿童之所以对数学难以“有感觉”，甚至经常深陷困境，大部分是缘于他们头脑中始终无法清晰地进行分类，难以发现事物之间的共性与区别。因此，作为抽象的重要环节，教师还是应该适时提醒学生有意识地进行“比较与分类”的数学化思考，从而强化抽象的意识与能力，毕竟数学思想的培育才是数学教育的使命所在。

4.次序化和序列化

次序化和序列化思维，或称之为“有序思考”，是优秀思维品质必不可少的要素。抽象思维之所以能充分体现出全面性、严谨性，与序列化的处理信息以及有序思考的思维习惯密切相关。皮亚杰认为：“在儿童思维中有一种非常原始的关于次序的结构——序列化结构，它象分类结构一样原始。[7]”“沏茶问题”中一个重要的教学活动就是要帮助学生厘清各种工序的“先后顺序”，认识到哪些次序不变，哪些次序可以变换，如“洗水壶——接水——烧水”的先后顺序就不能变，而在烧水时可同时进行的“找茶叶与洗茶具”就可以变换顺序。教师切莫因为这里的“次序化与序列化”比较容易理解就一带而过，恰好相反，这正是强化学生有序思考的好机会。

5.数量刻画

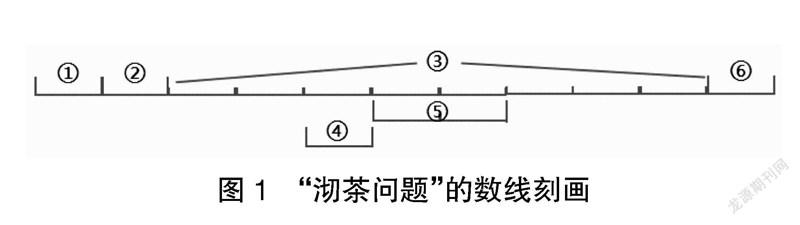
人的理性认识的“大厦”是以抽象能力作为基石的，而数学抽象的建立又是抽象能力形成的主要标志。有数学家指出，数学说到底就是抽象的学问。数学抽象思想最为鲜明的特征就是对客观事物或直观表象进行“数量刻画”。将具体的事物用相应的“数据”或“数量”进行抽象的表达，继而进行符号化、形式化的分析，以便更进一步地进行逻辑推理。在“沏茶问题”中，教师通常都能够关注到“有序思考”，并继而以流程图（简单的数学问题解决模型）的形式反映问题解决的策略，但是所采用的“刻画”方式多以“文字结合箭头”为主，缺少了最能反映抽象力量的“数量刻画”。此时，教师若采用“数线”的方式，将沏茶的各项工序及流程刻画出来，则能尽显数学刻画的简洁明了。如，以1个单位的线段代表1分钟，八个单位自然就代表8分钟，线段的前后顺序也就是工序的先后顺序，线段上下摆放可表示包含关系，即代表可以同时做的两类事物（见图1）。

“数线”这一名称引自柯普兰在《儿童怎样学习数学——皮亚杰研究的教育意义》一书中的的表述，他指出：“数线是个有用的发明，它能帮助所有儿童把算数的概念具体化。”“数线”不仅能够直接反映出完成各工序的时间，而且能直接表达出总用时，把不同的完成工作的方法以相应的“数线”表示出来，更易于对比。特别是在解决“不完全包含”的几类事物时进行“数线”刻画，其直观优势更为明显。这种“数线”刻画突显了数学问题解决形式的严谨与简约，充满抽象的味道，学生也会受到较强的思维触动，从而对抽象过程的认识更深入，抽象素养也会得到较好的培育。

三、“沏茶问题”教学目标的建议

基于上面的分析，笔者建议教师在教学“沏茶问题”时应将教学目标定位于“数学抽象思想的教与学”层面，以培养学生数学思想为核心任务开展课堂教学。在教学中，通过解决“沏茶问题”这一简单生活事例，使学生经历“简化与命名、一一对应、比较与分类、次序化和序列化、数量刻画”等具体的抽象思维活动过程，并通过对比、质疑、优化等探究活动，体验解决问题策略的多样性，积累数学活动经验，培养“抽象”的学科核心素养，感悟“用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界”的数学学习的意义。

胡塞尔说：“世界本身必须是理性的世界，这种理性是在数学的自然中所获得的新的意义的理性。[8]”胡塞尔所说的“理性”即为科学理性精神，科学理性精神在数学中的显著特点就在于以数学化的思维认识世界，而数学化思维的核心就是“抽象”。数学教师无疑要担起培养学生抽象能力与素养的任务，通过教学促使学生内化抽象思想，树立理性精神。总之，在数学的教与学的完整历程中，对师生都不可或缺的就是——让“抽象”真实发生。

参考文献

[1]林夏冰.数学哲学译文集[M].北京：知识出版社，1996：58.

[2]M.克莱因.古今数学思想（1）[M].张理京，张锦炎，江泽涵，译.上海：上海科学技术出版社，2014.

[3]史宁中.数学思想概论——数量与数量关系抽象[M].长春：东北师范大学出版社，2015：3.

[4][7]皮亚杰.发生认识论原理[M].王宪钿，译.北京：商务印书馆，1981.

[5][6]柯普兰.儿童怎样学习数学——皮亚杰研究的教育含义[M].李其维，唐请镳，译.上海：上海教育出版社，1985：61，64.

[8]胡塞尔.欧洲科学危机和超验现象学[M].张庆熊，译.上海：上海译文出版社，1988：72.

郑义富，广东省中山市西区中心小学校长、西区中心小学集团校长，正高级教师;广东省特级教师，广东省名校长工作室主持人，兼任中山市人民政府责任督学，华南师范大学硕士研究生导师。主持国家、省、市级课题并取得科研成果十余项，在国家级刊物发表论文30余篇，著有《解放心灵的课堂》《为人格盛开》等著作。

作者简介：郑义富，广东省中山市西区中心小学校长、特级教师，华南师范大学教育科学学院博士研究生，E-mail：1598138422@qq.com（广东广州，510631 ）