结构化思维教学的实施策略

袁恩忠

【摘   要】结构化思维教学能让学生经历“理解（隐性思维显性化）→重构（显性思维结构化）→呈现（结构化思维形象化）”的思维过程，改变小学数学课堂中长期存在的“碎片化”教学的现状。具体实施策略有以下三条：整合重组学习材料，进行概念联结，实现内容材料结构化;整体推进教学过程，进行生成建构，实现教学进程结构化;分项落实思维评测，进行思维干预，实现评价输出结构化。

【关键词】结构化思维;策略;路径

所谓“结构化思维”，是指以探寻事物结构为目标，积极建构事物组成部分之间的关联，以得出事物发展一般规律的一种思维方法。“结构化”包含两层含义，即结构化教学和结构化思维。前者是手段和路径，后者是目标和价值取向（如图1）。通过实施内容材料结构化、教学进程结构化和评价输出结构化等教学策略，让学生经历“理解（隐性思维显性化）→重构（显性思维结构化）→呈现（结构化思维形象化）”的思维过程，实现数学思维从零散状向结构化的转化。

现行数学教学存在以下三个问题：一是学习素材缺乏关联性。教师不能解读教材的整体目标，没有关注到知识系统的整体性、关联性、结构性。二是课堂反馈缺乏结构性。突出表现为问题设计缺乏目标性、层级性和挑战性。三是思维评测缺乏有效性。多数教师只关注学习活动设计，很少对学生结构化思维发展状况进行“捕捉”与评测，更缺少评测工具。

针对上述问题，笔者开展了有关小学生数学结构化思维教学的研究，总结出以下实施策略。

一、整合重组学习材料，进行概念联结，实现内容材料结构化

根据学科逻辑和学生立场，需要对教材进行适度整合，设计出有利于学生数学结构化思维发展的学习材料。

（一）沿着“一条主线”：合理把握“单元整体观念”这条主线

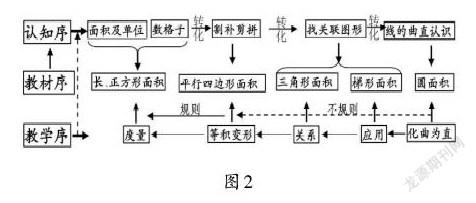
单元整体观念依据本单元教学内容的核心本质而建立，指向的是学生的理解和迁移，是单元教学整合设计的灵魂，具有统领性、隐蔽性和阶段性等特点，找准并合理把握这条主线，是实现内容材料结构化的关键。比如，小学阶段“平面图形的面积计算”本质上是通过转化进行面积单位的累加，沿着这条主线，可切分为若干个不同的课时目标（如图2）。

（二）把握“两个维度”：进行横向和纵向两个不同维度的整合

1.“横向整合”是指把“整体观念”下并列的知识内容整合起来，横向联结形成结构，以深化学生对概念的理解，帮助学生完善认知结构。比如，以“测量”为学习主题，将人教版教材三年级上册“时、分、秒”和“测量”两个单元进行跨单元统整，帮助学生理解时间、长度和质量可度量的属性，优化单元结构。

2.“纵向整合”是指把“具体观念”下具有从属关系的知识内容整合起来，纵向链接形成结构，深化对概念“内涵”与“外延”的理解，帮助学生迭代认知结构。比如，教学人教版教材二年级上册“角的初步认识”单元，可以将“角的初步认识”“认识直角”“认识钝角”3课时的内容整合成1课时，以“从角的大小感悟角的本质”为主线展开教学。

（三）站位“三个视角”：立足领域、单元和课时三个视角的整合

1.“领域视角”整合是指在某领域范围内打破单元边界，把人为切分的知识板块还原后作为学习主题整体呈现，实现“结构化”。

2.“单元视角”整合是指在单元范围内打破课时边界，将分散的知识内容整合起来，实现“结构化”。根据小学数学教材中单元间的知识内容呈平行编排的特点，宜采用整体呈现的方式进行整体建构学习。如将人教版教材二年级上册第四、六单元的教学内容整合如下：“表内乘法（一）”中的“5的乘法口诀”“2、3、4的乘法口诀”“6的乘法口诀”和“表内乘法（二）”中的“7的乘法口诀”“8的乘法口诀”“9的乘法口诀”共计6课时，整合成乘法口诀（学习全部45句口诀）、口诀练习、拓展课（从不同的方向拓展）等3课时。

3.“课时视角”整合是指在课时内实行知识点融合，采用项目化主题实践活动进行整合，实现“结构化”。如“统计图”系列课时设计时，可着眼于统计图知识链、能力链的形成与生长。沿着“画图→读图→选图”的学习路径进行整体建构学习，即先借助“画图”自主建立知识的结构性，再利用“读图”体现观念形成的序列性，最后通过“选图”体会表征的适切性，让学生经历结构化的学习过程。

二、整体推进教学过程，进行生成建构，实现教学进程结构化

要实现教学进程的结构化，重在引导学生经历“理解→重构→呈现”的结构化思维进阶过程，具体包括以下四大环节：设置问题场景→搭建学习支架→动态建构新知→强化认知结构。具体操作策略如下。

（一）设置问题场景，用结构化问题“扩大”思维空间

教师在设计教学时，可以对核心问题进行项目化处理，在课堂动态资源生成中，不断调整问题指向的空间，形成有逻辑结构的“问题串”。在教学实施过程中，可采用“递进式”“并列式”或“总分式”等方式逐层推进，引导学生思考“是什么”“为什么”“怎么样”“还可以怎样”等。

（二）搭建学习支架，用整体性建构“替代”重复建构

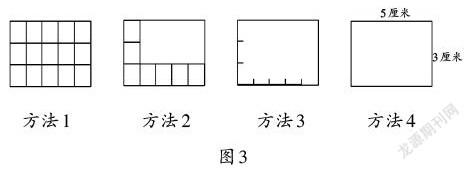
教师在引导学生进行深层次思考与交流时，可用典型性反馈材料进行整体呈现，帮助学生建立清晰的知识结构以及获得知识的方法结构。比如，教学人教版教材三年级下册“长方形、正方形面积的计算”时，教师整体呈现如下作品（如图3）。

从以上四种方法中可以发现，方法1到方法4能够帮助学生建立面积计算的模型，而方法4到方法1则体现了度量的思想方法。

（三）动态建构新知，用结构化反馈“助推”思维进阶

结构化反馈过程中，教师可采用“串联式”“并联式”两种反馈方式，展开求同、求展、求联思辨，帮助学生不断构建深层次的认知体系。比如，上述四种方法可进行如下“并联式”反馈。

问题1：“四种不同的方法，有什么相同的地方吗？”通过对这个问题的思辨與交流，达到思维求同的目的，即虽然方法不同，但本质相同——用面积单位测量，建立“长方形面积=长×宽”这个模型，实现面积单位的度量由计数到计算的转换。

问题2：“为什么两个长度单位相乘就是面积？”提出这个问题就是要让学生明白，虽然看到的是长与宽，但它们分别表示一行可以放几个面积单位，可以放几行，两个长度相乘的结果表示的是长方形里所摆放的面积单位的总个数，从而体会面积计算方法的由来。

（四）强化认知结构，用结构化练习“评估”思维水平

结构化练习之间的“关联”在于思维的“关联”，既要把握知识关联点，还要切准思维生长点。更为重要的是，通过策略的比较、分析和评价，促进学生对知识之间关联的理解，帮助学生形成结构化思维。比如教学人教版教材六年级下册“圆柱的体积”，可以设计如下结构化练习题组。

下面4个图形的面积都是36dm2（图中单位：dm）。将这些图形按水平方向分别卷成圆柱，哪个圆柱的体积最小？ 哪个圆柱的体积最大？你有什么发现？

反馈时，不仅要关注“数”与“形”的关联，从圆柱底面半径、高与体积之间的对应关系入手，还要关注卷成的圆柱形状，最后将思维顺势引导到“面”（长方形）跟“体”（圆柱）的关系上来。

三、分项落实思维评测，进行思维干预，实现评价输出结构化

根据“类比”“迁移”“整体建构”等结构化思维要素，笔者带领团队成员拟定出“小学生数学结构化思维水平评价指标要素与水平划分”量规（如表1，以下简称“量规”）。在评测过程中，形成了如下输出策略。

（一）设计蕴含思维结构层次的表现性评價任务

1.解释说明型表现性评价任务：以阐述说明概念本质、数学理解为主，生成建构知识学习过程的学习任务。以“圆的认识”的教学为例，设计了表现性任务“套圈公平”：“请你随意组建至少3位同学参与的套圈游戏，让他们怎样站位才公平？请画图并说明理由。”同时思考两个问题：“设计游戏时，你运用了哪些知识和经验？实施过程中有什么发现或困惑？”该任务以“学习单”的形式展开教学，根据任务和“量规”，对应设计侧重指向“生成建构”要素的评价量表，并进行思维评测。

2.问题解决型表现性评价任务：以真实情境下的问题解决为主，将所思所想表现出来，实现思维方法迁移的学习任务。问题解决型表现性评价任务关注内隐过程的评价，侧重指向“类比”要素的思维评测。比如，人教版教材二年级下册单元主题拓展“图形的拼组”，可设计任务：“分别用8、9、12、16个小正方形拼不同的长方形。”根据任务和“量规”，对应设计评测量表进行思维评测。

3.操作与制作型表现性评价任务：以知识梳理与验证为主，设计出知识、方法以及数学思想系统整理与应用的学习任务。比如，可将人教版教材一年级上册“认识钟表”这一内容改为主题项目学习“我与时间赛跑”，在钟面的制作过程中培养学生系统思考布局的能力，根据思维导图进行思维评测。

（二）预设课堂教学环节干预点

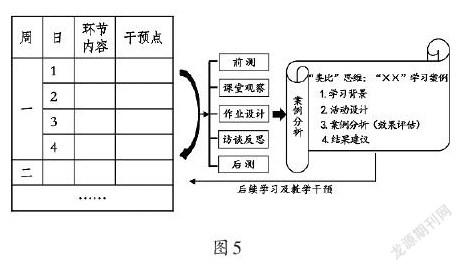
根据“生成建构”“类比”“迁移”结构化思维三要素，可以预设教学环节干预点（如图4），开展课堂实录观察，捕捉学生数学结构化思维发展状况。除此之外，还可以对应设计“环节干预案例分析模板”（如图5），用于教师主动反思环节思维目标达成情况，并及时进行教学跟进。

（三）搭建主题项目式内隐过程评价框架

内隐过程评价指向学生的结构化思维评测，一般放在学习过程中或者期末综合绿色评价中。比如，选择学生熟悉的事物——“豆子”，根据课程标准和学科特点设计以“豆子”为主题的绿色评价方式。将数学课中“估测豆子的数量”与科学课中“豆子是如何生长的”以及美术课中“用豆子贴画”进行整合。一颗小小的豆子，串联了多个学科知识，优化了学习方式，发展了学生的结构化思维。

总之，结构化思维教学不仅解决了小学数学教师长期单课时备课、根据教材按部就班低效上课的现状，还为数学学科校本教研提供了研讨范式，促进了一线数学教师的专业成长。

参考文献：

[1]潘牡牡.结构找源头，突出概念本质[J].教学月刊·小学版（数学），2020（12）.

[2]斯苗儿，陈国权，王丽芳.整合与拓展课例精选[M].上海：文汇出版社，2020.

[3]赵炯美，鲍建生.中小学数学课程中的一条主线：度量[J].小学教学（数学版），2017（10）.

[4]杨海荣.小学数学结构化课程整合的实践与研究[J].小学数学教师，2021（7/8）.

（浙江省湖州市安吉县报福小学   313301）