丰富教学素材，贴近学生学习

张侨平 慈艳

一、引言

数学教学离不开带领学生解决数学问题。培养学生数学问题解决能力是数学教育的重要目标之一。《义务教育数学课程标准（2011年版）》（以下简称《课标》）在第一学段目标中提出，学生要能“从日常生活中发现和提出简单的数学问题，并尝试解决;了解分析问题和解决问题的一些基本方法，知道同一个问题可以有不同的解决方法”;在第二学段目标中提出，学生要能“探索分析和解决简单问题的有效方法，了解解决问题方法的多样性……能回顾解决问题的过程，初步判断结果的合理性”。因此，为了让学生感受和经历问题解决方法的有效性和多样性，教师在教学中按照课程要求布置学习任务，提供适切的、有启发性的数学问题情境，显得尤为重要[1]。然而教师在实际的课堂教学中会面临学生解题能力存在巨大差异的现实。对于较为典型的数学问题，有些学生由于超前学习或者课后补习等原因，掌握了不少“便捷”的解法，而另一些学生却还是初次面对。教师通过对同样的数学问题的讲解和布置，既要整体提升学生的问题解决能力，又要照顾不同学生的学习差异，这是一个不小的挑战。

以小学第二学段教材中的“鸡兔同笼”问题为例，教师尝试通过对教学内容设计的改进，以达到让“人人学有价值的数学”“不同的人有不同的收获”的目的。期望结合对改进后的教学过程、实施效果的分析与反思，给教师提供些许教学启示，从而提升我们的数学教学效果。

二、教学内容背景

“鸡兔同笼”是北师大版教材五年级上册的学习内容，在“数学好玩”单元的“尝试与猜测”中。教材先以中国古代数学史书《孙子算经》作为背景：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”引发思考和讨论，并提出列表的方法引导学生进行合理的猜想，找寻问题中的规律，从而解决问题。“尝试和猜测”是问题解决的一种常见策略，这部分教学需要教师以“鸡兔同笼”问题为例，在教授学生这道古算题的解题思路和方法的同时，培养学生解决类似问题（如教材中提到的储蓄罐问题）的能力。

从教材内容设计上看，教学思路清楚明白。教师若依从教材的安排进行教学似乎很容易操作，比如可以从特殊例子开始，以学生间问答对话的形式逐步推进教学过程，在发展学生推理能力的同时，引导学生发现问题的解决方法。不过，在实际教学中，这一过程仍存在很多困难和问题。首先，在问题背景方面，“鸡兔同笼”作为有代表性的中国古代数学题，自然有其价值，但作为应用问题，对学生而言并不那么现实与合理（我们很少会把兔和鸡关在同一个笼子里）。即使作为数学历史和文化知识进行介绍，对小学生来说，也距离甚远，学生理解能力有限。其次，从教学目标来看，“鸡兔同笼”课题涉及的内容比较多，既包含数学文化的介绍，也蕴含着猜想、总结两个量的变化关系，以及探寻数值变化规律等内容。再次，从教材中呈现的解题方法来看，问题涉及兔和鸡两个变化的量，对于五年级的学生来说，尝试、列举数值的过程并不算困难，但学生往往对一一列举感觉到比较麻烦。最后，从课堂教学实施来看，教师经常需要面对学生在这类问题上表现出的较大的学习差异：一部分学生不知道这一问题的任何背景和方法，另一部分学生则已经通过超前学习等了解了“鸡兔同笼”的背景，学过“便捷”的问题解决方法（如方程法、假设法、抬腿法1）。教师在课堂上常常是还未开口讲解，学生“知道”之声便此起彼伏，教学中多数学生懒于静下心来在列表中通过猜测与尝试呈现鸡兔数量与腿数量的变化过程（亦即按照教材的内容编排），难以从变化中找到两个量之间的关系。如何在考虑學生已有知识经验的基础上，重视教材内容的课堂教学效果，是教师进行本节课教学设计与课堂实施的主要挑战。

三、两种教学设计的比较

面对前文提及的教学挑战，教师该如何应对？是按照教材的编排顺序按部就班地讲授，还是对教学内容进行重新设计和调整？如果进行重新设计，怎样能够帮助学生理解“鸡兔同笼”这一类数学问题的本质，并有效达成单元教学目标（比如掌握尝试法）呢？带着这样的思考，教师对两个小学五年级平行班级进行了不同的教学设计尝试，并在教学前后分别进行了调查分析。

教学时，在甲班采取遵循教材设计的流程，直接提出“鸡兔同笼”问题，教授尝试法，在此之后以另一道类似的古代算术经典问题“百僧与馍的问题：一百馍一百僧，大僧每人三个馍，小僧三人分一馍，大小僧人各几人”，作为课后的巩固练习，探讨大和尚与小和尚两个量的关系。据此，甲班的课堂教学流程可概括为图1所示。

在乙班则采用先提出并探讨“百僧与馍”的问题，再将“鸡兔同笼”作为课后评估与巩固的方式进行教学。这一设计主要是为了避开学生中可能存在的“重复学习”，引发学生的探究兴趣，先确保学生能够充分参与到尝试法解题策略的体验与学习中，再以教材中熟悉的例子作为问题解决策略应用的情境。乙班的课堂教学流程及课堂板书分别如图2和图3所示。

两个班的教学设计都包含了两个经典的中国数学历史问题，为学生提供了解我国古代数学文化的机会，二者的主要不同在于两个“问题”提出的先后顺序。甲、乙两班学生的总体水平相若，教学前教师对两个班级的学生进行了初步的询问调查，结果发现每班均有三分之二左右的学生提前学习过“鸡兔同笼”内容。

课堂上的教学数据表明：甲班（32人）在运用尝试法解决“鸡兔同笼”问题后，在练习环节只有65.6%的人能够正确解决“百僧与馍”的问题，正确解决问题的学生中有71.4%使用了尝试法;乙班（34人）在课堂上一开始就解决“百僧与馍”的问题，这时的正确率只有17.1%，正确的人中有33.3%使用了尝试法，但在随后“鸡兔同笼”的巩固练习中，使用尝试法解题的人数明显增多。

在运用尝试法的教学完成后，两个班最后均利用以下两个问题作为应用巩固。其中巩固问题1期望学生能将大船和小船分别跟“兔”和“鸡”对应起来;巩固问题2与教材的题目类似，作为生活中数学的延伸。

巩固问题1（租船问题）：38人共租了8条船，每条大船可坐6人，每条小船可坐4人，每条船都坐满了。问大船和小船各多少条？

巩固问题2（生活数学）：小明的储蓄罐里有1角和5角硬币共7枚，总值1.9元，问1角和5角的硬币各有多少枚？

课堂观察表明：尽管两个班的学生最后对“鸡兔同笼”问题的理解都比较深入，但在学习教材中的“尝试法”的时候，甲班绝大多数学生缺少兴趣，课堂气氛欠佳，需要靠教师不断维持纪律才能将列表尝试法教授完成。相比较之下，乙班学生能在自主解决问题中认可列表尝试法并完成学习任务。

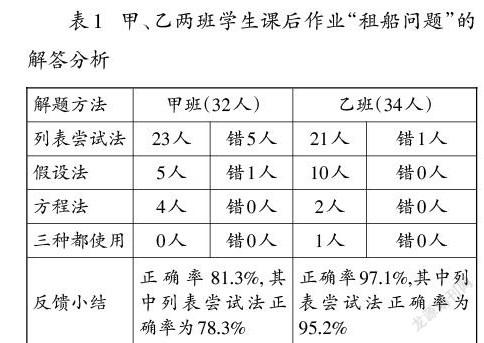
教学后，对甲、乙两班学生的课后作业情况进行了简要的统计分析，为便于说明，此处仅呈现作业中“租船问题”的数据统计结果（如表1）。

四、启示与反思

很多教师将经典的数学问题“鸡兔同笼”当作训练学生解题思维的重要素材。然而，发展学生的问题解决能力并非只是解题训练，教师更要帮助学生跳出“鸡兔同笼”的框架，看到和了解这类问题的本质。尽管上述我们介绍的只是在“鸡兔同笼”教学设计上的微小调整，但教学过程中学生表现出来的反应、解题表现以及后续的反馈，对于进行其他数学课题的教学，特别对于处理学生学习差异和进行数学问题解决的教学有一定的启发。

首先，教师要直面学生的学习差异。如前所述，课前超过一半的学生已经从不同的渠道学习或者接触过“鸡兔同笼”问题的解法，他们或已经无心再用教材所要求的尝试法去解题。教师需要在课堂教学中正视这一突出的现实情况，而不能一味地假定所有学生面对的都是“新知”。课程与教学设计的教育理论早已告诉我们，教师要清楚了解学生的课前经验是什么，有哪些基础，又有哪些局限，在此基础上去布置与设计教学[2]。更为重要的是，教师要考虑如何引导学生对他们假定自己已经知道的问题进行更为深入的探究与“尝试”。在乙班的处理上，教师有意避开学生的“已知”（知道“鸡兔同笼”以及各种解法），设计一个未知的但在内容本质上相同的问题情境，让学生暂时陷入“困境”。这样的设计处理，能解决学习差异的问题，使无论是所谓高起点还是低起点的学生，都能够参与到课堂学习活动中，共同进行讨论、分享和交流，并在这一过程中真实地暴露思维与困难，从活动中真正体会到尝试法的意义，掌握相应的解题策略。而且这样的教学处理也不会影响他们未来学习其他的解题方法，如假设法、方程法等。

其次，教学要重视学生的思维发展。“鸡兔同笼”问题不仅仅是鸡、兔“同笼”，学生还要关注到“鸡兔同笼”系列问题背后一般性的数学问题解题思路，不应只停留在“尝试—猜测”的思维层面。数学家波利亚（G. Pólya）在《怎样解题》一书中提到问题解决的“解题四部曲”：理解问题、设计解题策略、执行解题计划、回顾解答。

理解问题是学生解题和教师进行问题解决教学的第一步。在这个阶段，学生需要弄清楚问题是什么，具体包括：什么是已知量和未知量？它们之间的关系是什么？问题中给出的资料是不是足够？有没有什么资料是不相关的？这个问题难在哪里？等等。在上述“鸡兔同笼”问题中，如果学生面对的是任何一种动物（姑且叫动物A）在笼子里，相信他们比较容易知道A的数目。比如，若已知头的数目，一望便知A的数目;若已知腿的数目，做一点简单的除法也可知道A的数目。“鸡兔同笼”问题不同于以往单一未知量的问题，可以直接列出算式或方程解题（这里我们不去讨论算术方法和代数方法的优劣），这类问题的难点在于问题情境中涉及的两个未知的量（如头和脚），如何引导学生思考和处理变化的未知量是教学的关键。

在充分理解问题的基础上，可以着手对问题的解决策略进行设计。在“鸡兔同笼”问题的教学中，可以将学生解决单一量问题的经验作为教学的出发点，通过合适的提问，让学生先有解决一个未知量的体验（所谓假设法和抬腿法，本质上就是将两个未知量转化为一个未知量来处理，这正是以后初中阶段学习解二元一次方程组消元法的方法），然后再尝试去解决两个未知量的问题。这也是波利亚在问题解决第二阶段所提到的需要设计一些解题策略，即从简单情况开始尝试，如果不能解决所提出的问题，我们可以先解决一个与此有关的问题，想出一个更容易着手或者更特殊的问题。事实上，乙班教学中所运用的“百僧与馍”的问题情境正是这个策略。

在问题解决的第三阶段——执行解题计划中，涉及一些具体策略和方法的使用。常用的策略包括：尝试、猜测、列举、列表、绘图、试误、简化问题、寻找规律、逆向思考、逻辑推理、假设、穷尽、模拟和应用工具等等。从教材“数学好玩”整个单元的设计安排中可以看出，本节课中“尝试—猜测”是学生需要掌握的问题解决方法。在学习本节课的尝试法之前，教材还呈现了“设计秋游方案”“图形中的规律”等内容。这些内容是不是真的好玩我们未必能确定，但它们均涉及数学问题解决策略。弄明白了课题之间的关联性，教师在教授“鸡兔同笼”问题时就不会只是聚焦在鸡和兔的问题上，而是能利用其他类似的问题作为引入（如“百僧与馍”的问题）或是作为巩固和拓展（如租船问题），让学生看到问题之间的内在联系（比如问题的相似之处在哪里，解题思路的相似点在哪里等等），学生也不会觉得自己只是多做了一组数学题。这种关联性还能在更多的数学历史文化中找到共鸣，比如明朝程大位《算法统宗》中提到的“三足团鱼六眼龟”问题。在教学设计中提出这样的关联性比较，比单纯强调“鸡兔同笼”问题来自古代要有趣味和有意义得多。如果不理解这些教学策略的话，教师的讲授很可能变成只是完成教材的教学任务，学生掌握的知识和方法很可能也是碎片化的。

完成“鸡兔同笼”问题的讲解，检查完学生对解题方法的掌握情况后，教学是否就结束了呢？如果我们再看问题解决的第四阶段，就会发现检查答案的正确性、合理性只是回顾的一部分，教师还可以鼓励学生思考其他解题方法并将问题延伸，以增强学生的探究能力和对问题解决的认识。这也是《课标》中对学生问题解决能力的要求。例如，询问学生：所学的方法还能用于其他哪些问题？如果问题条件改变了，情况会怎样？在“鸡兔同笼”问题中，如果有第三种动物关进笼子，只知道它们的头的数目和腿的数目，还能确定每一种动物的数目吗？如果教师能够创造条件并引导学生提出这样的问题，那么，学生的数学问题解决能力就提升了。

参考文献：

[1]张侨平.数学问题解决与数学活动题[J].小學教学（数学版），2020（4）：12-14.

[2]泰勒.课程与教学的基本原理[M].施良方，译.北京：人民教育出版社，1990.

（1.香港教育大学数学与资讯科技学系   999077

2.北京市海淀区华清嘉园中关村第二小学   100089）