典型激励下电磁-碰撞复合阻尼系统减震特性研究

胡 溧, 李 想, 杨啟梁, 王 博, 王华伟

(武汉科技大学 汽车与交通工程学院，武汉 430081)

近年来，建筑物高度不断攀升，建筑受风载激励后振幅大幅上升。为满足社会生产生活需要，对高层建筑结构开展振动抑制研究显得至关重要。在工程应用中，常采取被动控制技术、半主动控制技术，以及主动控制技术对结构进行振动控制。

对于碰撞阻尼器(pounding tuned mass damper,PTMD)，Bapat等[1-2]等很早就对单质量PTMD碰撞机制展开研究；而近年来，闫安志等[3]采用Hertz碰撞模型描述碰撞力，建立两自由度系统模型，数值分析了结构参数对TMD的影响规律；Zhang等[4]基于Hertz接触定律构建PTMD模型，并将PTMD应用到输电线塔以提升抗振性能。对于电涡流阻尼器(tuned mass damper,TMD)，陈政清等[5]将其应用在桥梁和输电线塔等结构，试验证明该阻尼器减振效率高。

为进一步提升PTMD耗能效率，一批学者对PTMD和电涡流TMD相结合的新式电磁-碰撞复合阻尼器(eddy current-pounding tuned mass damper,EPTMD)展开了深入研究。林籽先等[6]对电磁-碰撞阻尼器耗能机理及减振效果进行了可行性分析；胡溧等[7]提出了一种电磁-碰撞复合阻尼系统，并对系统进行了理论和试验研究。

本文提出碰撞力模型描述碰撞过程，以等效黏性阻尼表示电磁阻尼，从而建立电磁-碰撞复合阻尼系统动力学模型。对模型动力学特性展开研究，并进行了试验验证。

1 电磁-碰撞复合阻尼系统动力学建模与仿真

电磁-碰撞复合阻尼系统模型如图1所示。主结构质量M通过刚度系数k1，黏性阻尼系数c1的弹簧与基础相连，外界激励p(t)。附加质量m受间隙为L的挡壁限制，运动时受电磁阻尼c3作用,且通过碰撞力F和摩擦力f与主结构相耦合。采用碰撞力模型描述碰撞过程，等效黏性阻尼表示电磁阻尼，并假定碰撞运动沿碰撞面法线方向，忽略空气阻尼影响。

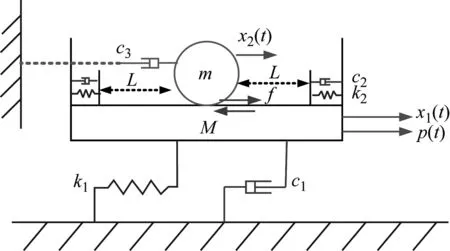
图1 电磁-碰撞复合阻尼系统模型

电磁-碰撞复合阻尼系统的运动特性可用运动学方程描述为

碰撞力：

δ(t)=|x1(t)-x2(t)|-L

(6)

(7)

碰撞过程中最大弹力：

(8)

碰撞力方向判断：

正压力：

FN=mg

(11)

摩擦力：

f=μFN

(12)

摩擦力方向判断：

外界激励：

p(t)

(16)

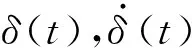
黏弹性材料残余表面变形率：

(17)

根据碰撞过程中能量守恒，碰撞刚度系数k2、碰撞阻尼系数c2、碰撞恢复系数e及黏弹性材料残余表面变形率e1应满足下列方程

(18)

对于电磁阻尼c3进行理论计算，假设在导体内取一微小单元，其长、宽、高分别为db、da、dt。并将该单元放置于磁感应强度为B的匀强磁场中，导体电阻率为ρ。根据电源输出功率最大化条件，通过安培定律推导求得电磁阻尼理论值c3为

(19)

表1 电磁-碰撞复合阻尼系统主要参数

电磁-碰撞复合阻尼系统主结构振幅下降速度最为明显，如图2所示。经过碰撞力、电磁阻力以及摩擦力作用，输入系统的能量得以快速耗散，在第2.23 s时主结构振幅已衰减到0.001 m。碰撞阻尼系统主结构振幅衰减到0.001 m需2.739 s，而无电磁无碰撞阻尼系统主结构振幅衰减到0.001 m则需3.25 s。在给定相同初始条件下系统自由振动，电磁-碰撞复合阻尼系统减震效果最好，碰撞阻尼系统次之，无电磁无碰撞阻尼系统最差。

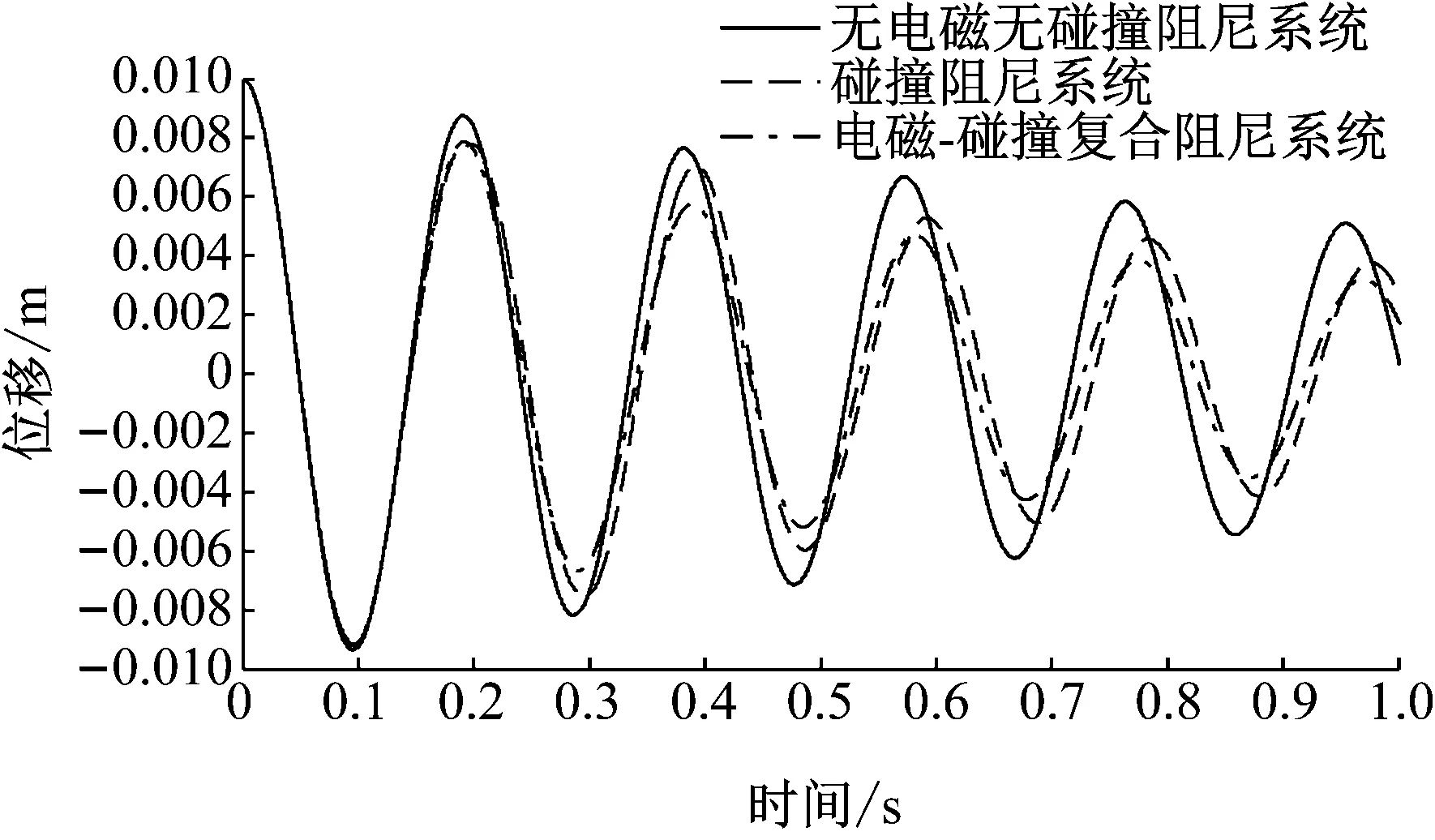
图2 自由振动下3种系统主结构位移时程曲线

2 试验验证

2.1 电磁-碰撞复合阻尼系统试验装置与测试系统

试验装置包括主结构限位盒装置M，铜柱m，钢片(刚度系数k1，阻尼系数c1)以及磁场发生器装置，如图3所示。测试系统包括LabVIEW信号采集分析系统和基恩士IL-100系列CMOS激光位移传感器。试验装置参数为：M=0.923 kg,m=0.045 kg,L=0.01 m,k1=1 000 N/m。

2.2 试验效果

对试验装置右端钢片施加向右0.01 m的初始位移激励,主结构自由振动。与此同时激光位移传感器监测主结构运动位移，LabVIEW信号采集系统采集保存数据，并利用Matlab对数据进行拟合绘图。现将仿真结果与物理试验测试数据进行比对，结果如图4所示。

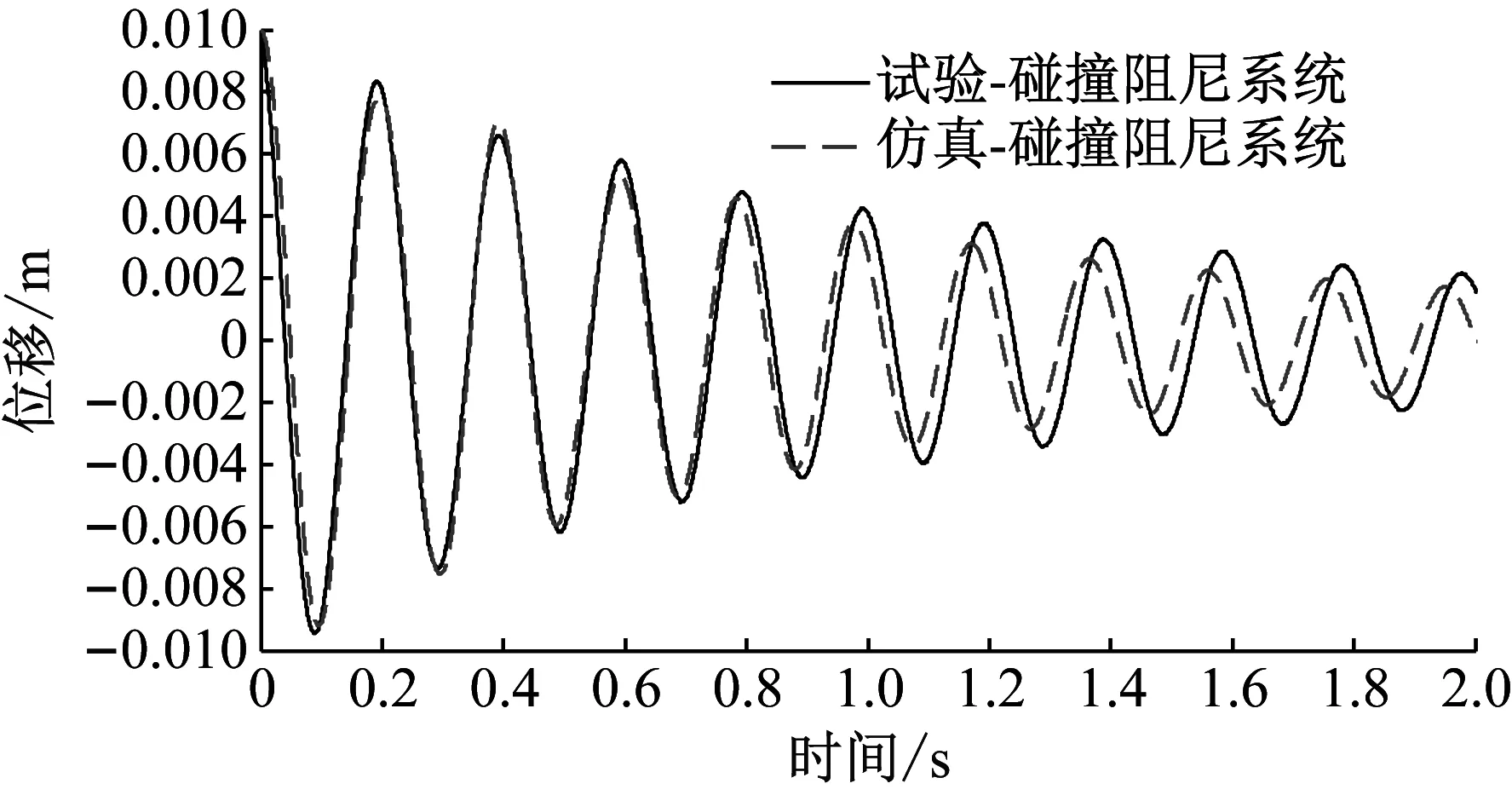
图4 碰撞阻尼系统仿真与试验主结构位移时程曲线

由图4可知，碰撞阻尼系统，仿真与试验在前半段(0～1.0 s)两者的位移时程曲线非常吻合。而后半段(1～2.0 s)两者相差较大，但均呈现缓慢地衰减,近似等幅度简谐运动。主要原因是碰撞消失，系统处于单自由度自振状态。选取前4个波峰幅值与试验测试数据进行比对，相对误差均控制在±10%以内，如表2所示。

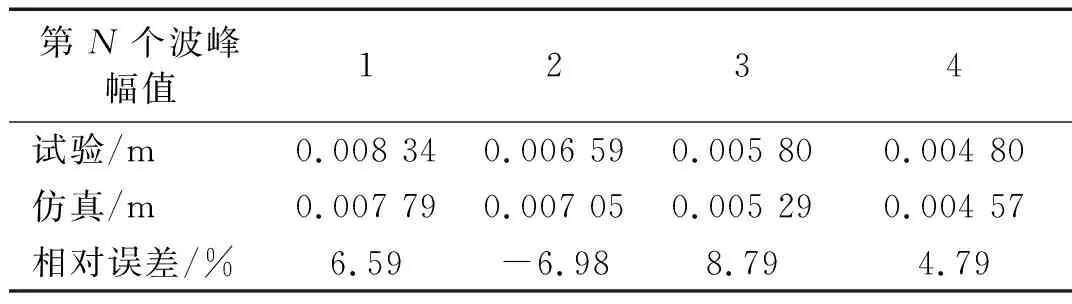
表2 碰撞阻尼系统仿真与实验主结构波峰幅值

电磁-碰撞复合阻尼系统，仿真与试验在前半段(0～1.2 s)两者的位移时程曲线吻合度较高，而后半段(1～1.2 s)两者相差较大，如图5所示。选取前4个波峰幅值与试验测试数据进行比对，相对误差均控制在5%以内，如表3所示。

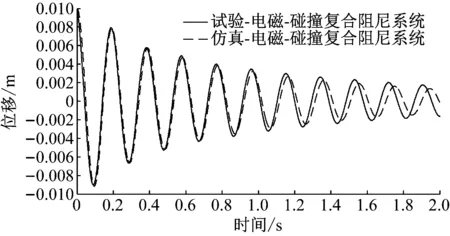
图5 电磁-碰撞复合阻尼系统仿真与试验主结构位移时程曲线

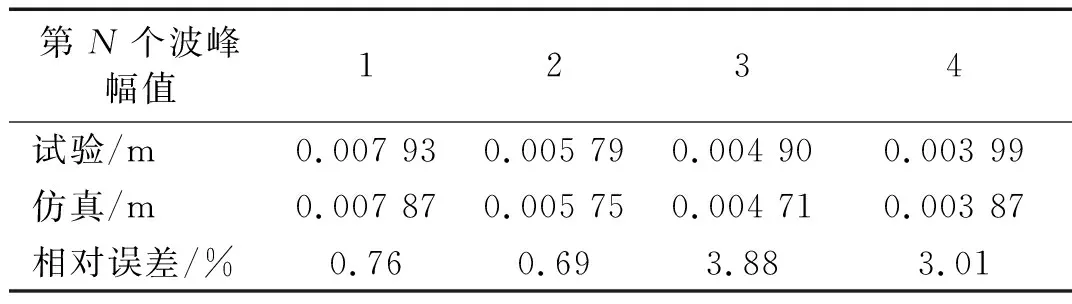
表3 电磁-碰撞复合阻尼系统仿真与试验主结构波峰幅值

综上所述，虽理论模型与物理试验结果存在偏差，但就减震效果而言，两者均能反映出电磁-碰撞复合阻尼系统能提升碰撞阻尼系统的耗能效率。结合表2和表3的数据分析可以确定所构建的电磁-碰撞复合阻尼系统动力学模型精确，结构参数取值合理。

3 外界激励条件下系统的减震特性分析

为验证电磁-碰撞复合阻尼系统在复杂环境中的减震效果，仿真设计了周期激励、非周期激励，对系统在不同激励条件下的减震性能进行相应探究。

系统的减震效果通过位移均方根值(root mean square,RMS)减震率来衡量

(20)

式中:η为位移均方根值减震率;RMS0为无控主结构位移均方根值;RMSctrl为受控主结构位移均方根值。

3.1 系统在简谐激励下的强迫振动

简谐激励下3种系统主结构位移如图6所示。

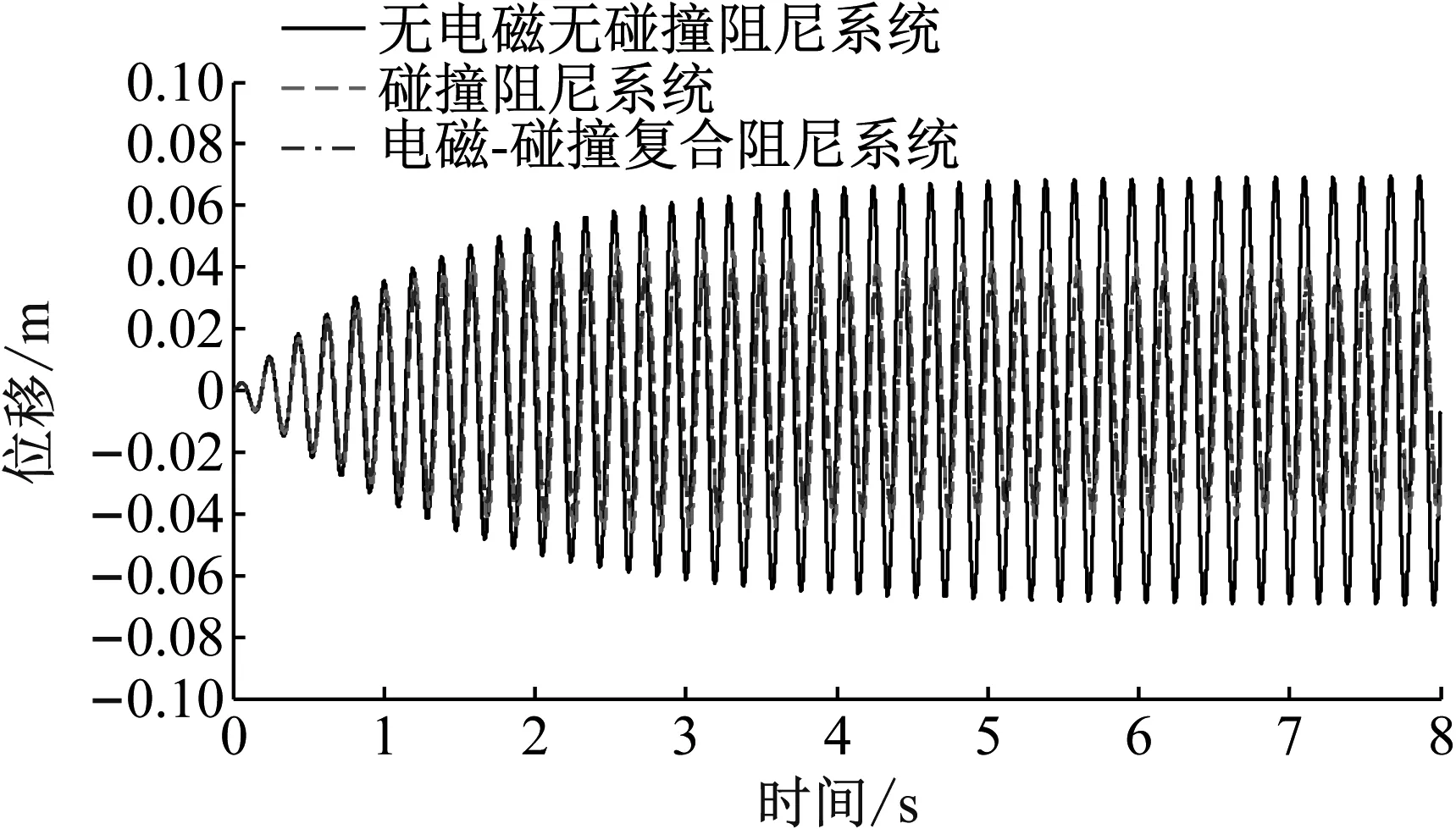
图6 简谐激励下3种系统主结构位移时程曲线

在周期简谐激励作用下，系统达到共振，待系统振幅达到稳定时(第5 s后)，电磁-碰撞阻尼系统的主结构振幅为0.036 04 m，低于碰撞阻尼系统振幅0.041 54 m，如表4所示。而电磁-碰撞复合阻尼系统的减震率为42.14%，高于碰撞阻尼系统33.07%的减震率。说明在周期简谐激励下，电磁-碰撞复合阻尼系统的减震性能优良。

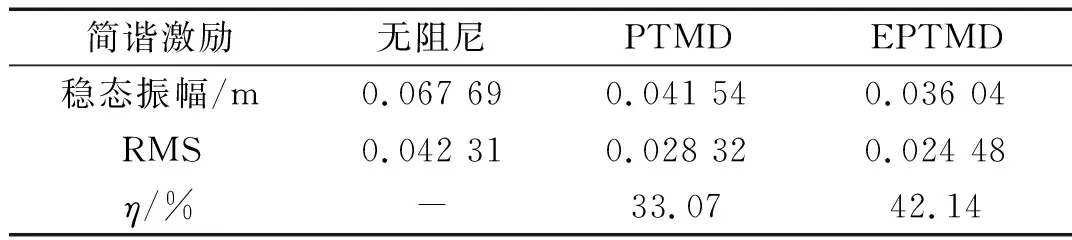
表4 简谐激励下系统水平向响应及减震率

为进一步探究电磁-碰撞复合阻尼系统的鲁棒性，现对外界调谐激励频率做±15%的偏移处理，对非调谐激励下的碰撞系统与电磁-碰撞复合阻尼系统减震性能进行了研究。

(1) 简谐激励频率失谐-15%时(如图7所示)

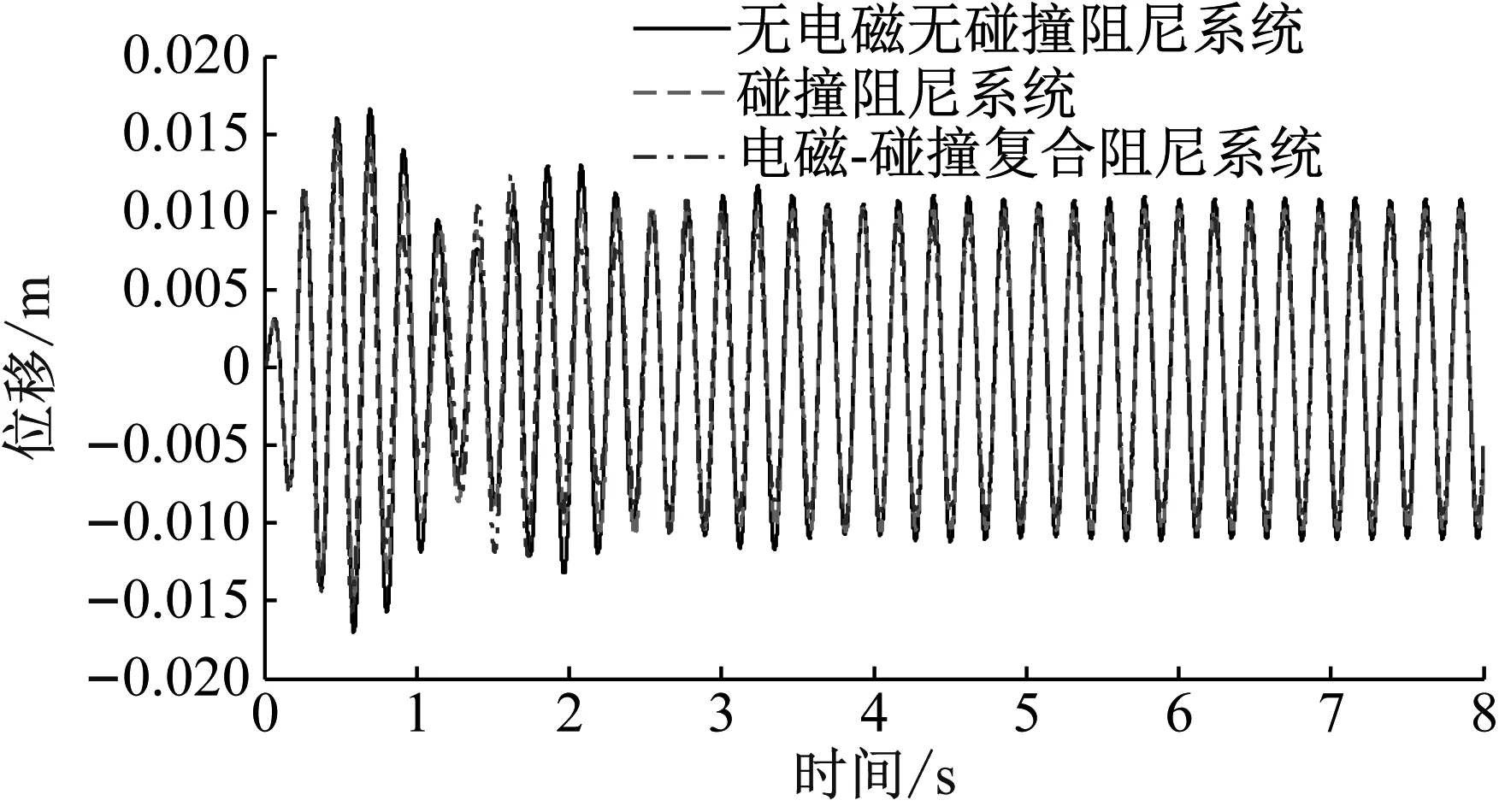
图7 简谐激励频率失谐-15%时3种系统主结构位移时程曲线

在简谐激励失谐-15%时，待系统主结构振幅响应达到稳定，电磁-碰撞复合阻尼系统主结构振幅为0.009 68 m低于碰撞阻尼系统的0.010 15 m，如表5所示。

表5 简谐激励频率失谐-15%时系统水平向响应及减震率

从减震率可知，电磁-碰撞复合阻尼系统仍有11.99%的减震率，高于碰撞阻尼系统6.94%的减震率,仍能发挥一定的减震性能。

(2) 简谐激励频率失谐+15%时(如图8所示)

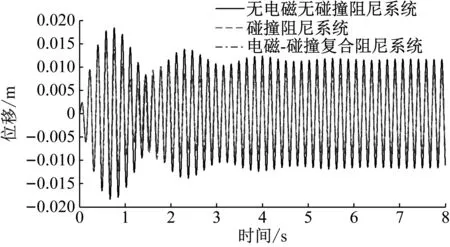
图8 简谐激励频率失谐+15%时3种系统主结构位移时程曲线

在简谐激励失谐+15%时，电磁-碰撞复合阻尼系统的稳态振幅仍低于碰撞阻尼系统的稳态振幅,如表6所示。而电磁-碰撞复合阻尼系统的减震率为25.56%，仍高于碰撞阻尼系统24.62%的减震率。

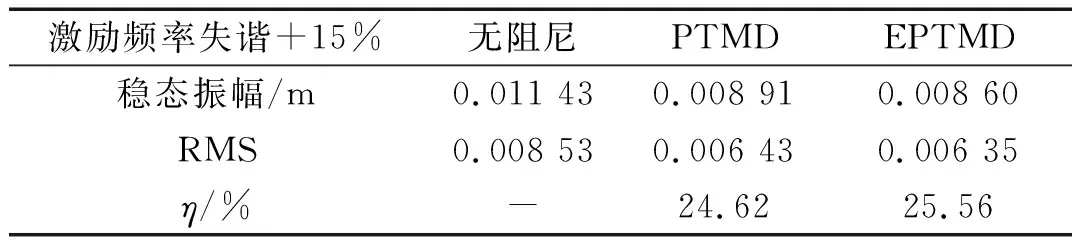
表6 简谐激励频率失谐+15%时系统水平向响应及减震率

由此可见，当外界激励频率发生一定程度失谐时，电磁-碰撞复合阻尼系统仍能发挥较好的减震性能。

3.2 系统在方波激励下的强迫振动

在方波激励下，系统处于共振，待系统振幅稳定时，系统主结构位移时程曲线如图9所示。电磁-碰撞复合阻尼系统振幅为0.023 14 m，比碰撞阻尼系统的振幅0.026 71 m要低，如表7所示。电磁-碰撞复合阻尼系统的减震率为45.11%，高于碰撞阻尼系统35.24%的减震率。

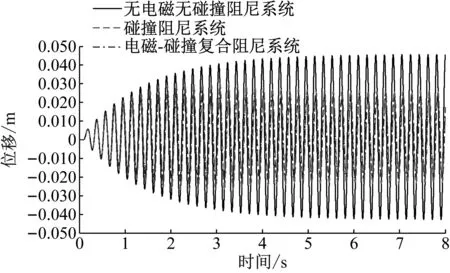
图9 方波激励下3种系统主结构位移时程曲线

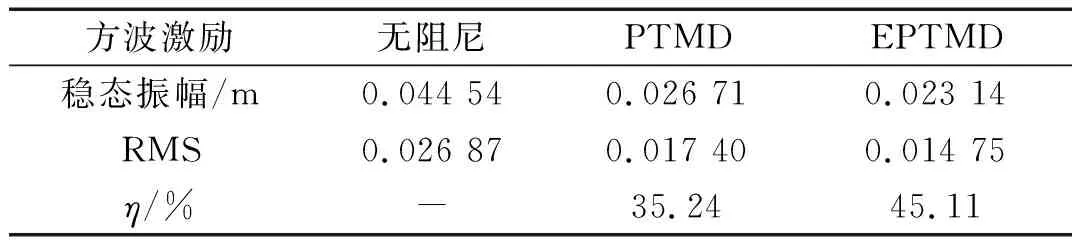
表7 方波激励下系统水平向响应及减震率

3.3 系统在锯齿波激励下的强迫振动

在锯齿波激励下，系统主结构位移过程曲线如图10所示。系统处于共振，待系统振幅稳定时，电磁-碰撞复合阻尼系统振幅为0.011 62 m，比碰撞阻尼系统的振幅0.013 30 m要低，如表8所示。同样，电磁-碰撞复合阻尼系统52.53%的减震率比碰撞阻尼系统42.35%的减震率要高。

图10 锯齿波激励下3种系统主结构位移时程曲线

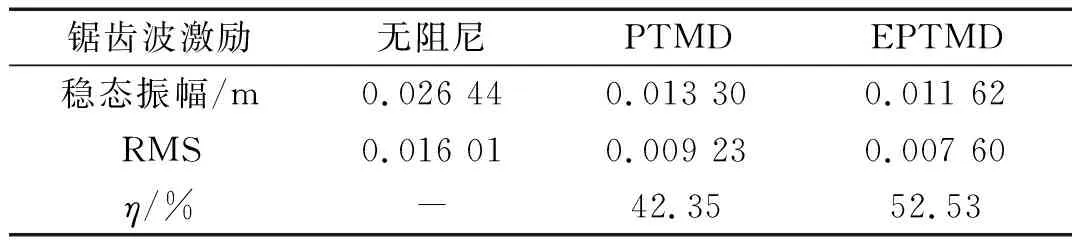
表8 锯齿波激励下系统水平向响应及减震率

3.4 系统在半正弦冲击激励下的强迫振动

对系统施加半正弦冲击激励，电磁-碰撞复合阻尼系统振幅衰减速度高于碰撞阻尼系统，减震性能良好，如图11所示。

3.5 系统在非周期激励下的强迫振动

对高斯白噪声频段加以限制，采用低通滤波器将频率限制在1～100 Hz内，对系统进行激励，其主结构位移过程如图12所示。

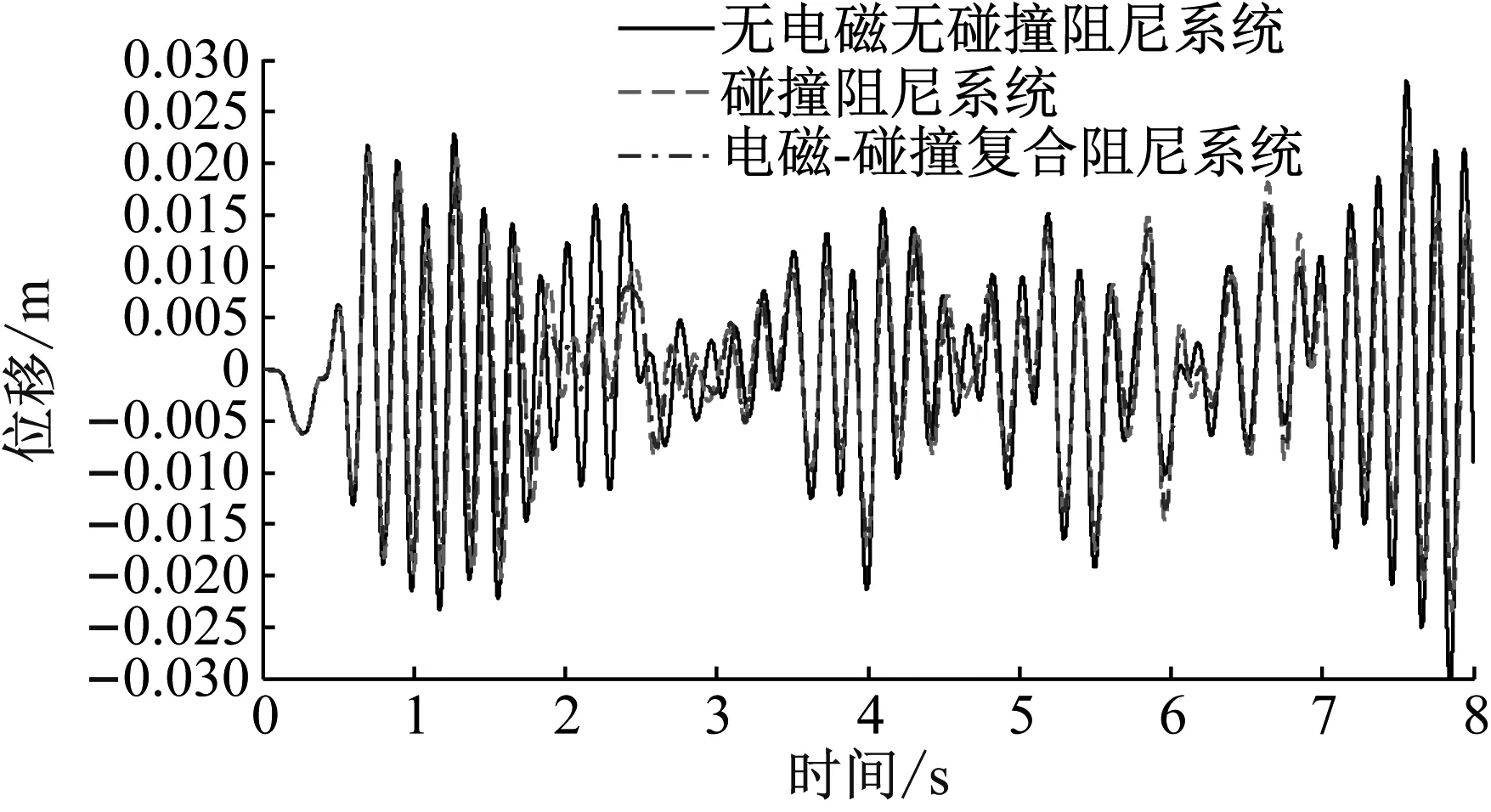
图12 非周期激励下3种系统主结构位移时程曲线

在非周期激励下，电磁-碰撞复合阻尼系统的减震率为20.59%，高于碰撞阻尼系统13.32%的减震率，如表9所示。

表9 非周期激励下系统水平向响应及减震率

通过对1～2 s,7～8 s时间段内系统主结构位移时程数据进行处理分析，发现激励频率在5～5.3 Hz频段内对系统主结构的位移响应影响最大。结合图12分析可知，在非周期激励下，电磁-碰撞复合阻尼系统的减震性能良好且稳定。

综上，利用所建理论模型，通过对系统在一系列给定外界激励条件下的响应进行仿真研究，结果表明,电磁-碰撞复合阻尼系统在周期激励下的减震效率更高，鲁棒性能良好，能够进一步提升碰撞阻尼系统的耗能效率，加快主结构的振动衰减。

4 结 论

本文研究了一种电磁-碰撞复合阻尼系统，提出了根据碰撞力模型和等效黏弹性阻尼建立的电磁-碰撞复合阻尼系统动力学模型，并进行了试验验证。结果表明电磁-碰撞复合阻尼系统能够加快主结构振动响应的衰减，进一步提升碰撞阻尼器耗能效率。仿真同样表明该电磁-碰撞复合阻尼系统具有良好的减震效果，并利用该模型探究了一系列外界激励对系统主结构的响应规律，对后续相关电磁-碰撞复合阻尼系统开发具有一定的指导意义。