基于可控电磁负刚度的半主动隔振器传递率特性研究
2022-05-04刘豫喜
孟 凯, 顾 勇, 刘豫喜, 马 涛
(1.河南工程学院 机械工程学院,郑州 451191;2.机械科学研究总院江苏分院有限公司 设计开发部,江苏 常州 213164)
刚度可控的振动隔离技术对一些加载质量和固有频率可变,大激励幅值振动隔离有需求的工业行业的发展起着至关重要的促进作用,例如:军事工业、汽车行业和超精密机械加工行业。这些行业对隔振技术有着特殊的需求,它们涉及振动线谱的降低和改造,振动耦合冲击的削弱和隔离,超低频振动的隔离等[1-6]。
根据线性隔振理论,要实现低频率的隔振,只能通过减小刚度或者增大质量的方法来实现。但是,减小系统的刚度会减弱隔振系统的承载能力或增大弹性单元的体积,而增大系统的质量会迅速增加隔振器的成本。从而,单纯降低隔振系统固有频率的方法在实际应用中受到了较大的限制。非线性的正负刚度并联隔振系统,可以实现隔振系统的准零刚度和高静态刚度、低动态刚度特性[7]。根据负刚度的构成方式,非线性正负刚度并联隔振器可分为机械式、永磁式和电磁式。
机械式结构是通过水平方向施加能随隔振对象垂直运动并与垂向运动同向的力,与垂向弹性元件支撑力并联实现刚度的降低。主要型式有“三弹簧”结构[8-11]和“欧拉曲屈梁”[12-13]结构。机械式负刚度结构具有强非线性的特点,在负刚度参数选择合适的情况下,位移的传递率表现优于线性系统。
永磁式结构是通过多个永磁体之间的斥力或吸力构成与隔振对象运动同向的力,与弹性元件的支撑力并联实现刚度的降低[14-16]。永磁式负刚度结构具有结构紧凑,无摩擦的优点。
电磁式结构是利用电磁铁的通电后形成的吸力形成与隔振对象运动同向的力,与弹性元件的支撑力并联实现刚度的降低[17-18]。电流的改变导致电磁力的变化,从而可以实现电流对刚度的控制。
机械式和永磁式结构承载能力大,隔振质量固定,而基于电磁铁原理的电磁式负刚度结构较复杂,在铁芯的磁滞作用下,电流对负刚度控制具有一定滞后性,其适用性受到一定限制。本文提出了一种基于线圈和永磁铁的可控负刚度的新结构,应用于正负刚度并联隔振器,克服了磁滞作用的影响,实现了对隔振质量变化敏感性低和刚度可变、可控的要求,并研究电磁负刚度的形成原理,对其力学性能进行解析表达,通过试验验证了基于可控负刚度隔振器的隔振性能和控制特性。
1 可控电磁负刚度
1.1 电磁负刚度原理
空气中的无磁性导体是最佳的磁电的转换介质,可以提供随电流变化的时变磁场,从而产生可控磁力。空气中的两个同轴分布的导电圆环,根据电流方向的不同,可以表现出来拉力或者斥力。由于两个导电圆环的电磁物理特性,图1(a)所示,当固定两个圆环中的一个,通入反向电流,另一个圆环在轴线方向由于受到电磁力的作用表现出来负刚度特性,加载电流的量值决定了负刚度的大小。
两个电流反向的载流圆环形成的负刚度过小,不能满足实际工况的隔振需求。增加电磁斥力是通过若干导电圆环的叠加生成线圈实现的,这不会影响电流对负刚度的控制效果。虽然,通过线圈叠加的方法可以增大部分电磁力,但是与永磁铁相比还是小的多。若负刚度由两线圈构成,则负刚度的控制性优异;若负刚度由两个轴向充磁的环形永磁铁构成,则负刚度的尺度远大于线圈构成的结构,但是这样却失去了负刚度的调节能力。综合考虑,用一个线圈和一个环形永磁铁构成负刚度结构,可同时兼顾较大的负刚度需求和负刚度可控制性,如图1(b)所示。
若在轴向固定距离上需要产生更大的负刚度,由于磁场的可叠加性,可以利用形状相同的线圈和环形永磁铁叠加实现。把图1(b)所示的厚度用两组电流方向和磁场极化强度方向相反的线圈-电磁铁组合,构成图1.2(c)所示的结构。在这个结构设置中,两个线圈电流的方向相反,两个永磁铁的极化方向也相反。两个永磁铁被外力沿轴向压制在一起,同时两个线圈的位置也相互固定。由于多层线圈和多层永磁铁的磁力叠加作用,负刚度在轴向固定距离上产生的负刚度更大。综上所述,图1(c)所示的结构更适用于正负刚度并联隔振系统设计。
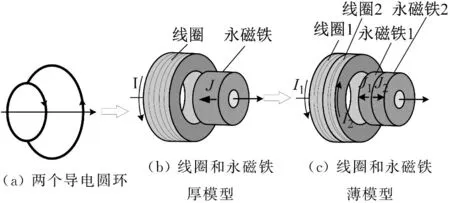
图1 负刚度原理模型
1.2 负刚度磁力和刚度计算
1.2.1 负刚度单元的叠加
为了获得更大的电磁力和负刚度,n个负刚度单元沿着轴向被叠加在一起,如图2所示。线圈和环形永磁铁分别沿轴向固定,数量都为n,Cp表示第p个线圈,Mq表示第q个永磁铁,根据磁场的叠加原理,轴向合电磁力FM可表示为
(1)
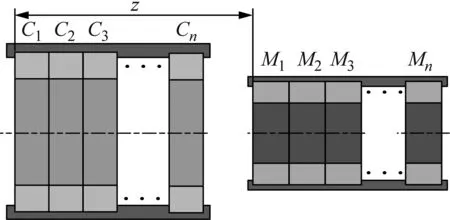
图2 负刚度单元叠加原理
式(1)对线圈和环形永磁铁的轴向位移Z求负导数可以得到负刚度kN的表达式为
(2)
只要得到单个线圈和环形永磁铁轴向磁力FCpMq,便可求得叠加后的磁力和刚度的表达式。
1.2.2 单个线圈和环形永磁铁轴向磁力计算
(1) 线圈和环形永磁铁模型的统一
虽然,安培环流理论和磁荷理论对磁力的计算具有同等的效果,但是,线圈磁力用安培环流理论计算较方便,而永磁铁磁力利用磁荷理论计算较方便。要计算包含线圈和环形永磁铁的磁力系统,必须统一其理论模型。
线圈是由若干层螺线管叠加而成的,而单个的螺线管可以等效为一个圆柱永磁铁[19]。一个高度为H,半径为R,圈数为V,电流为I的螺线管,可以等效为一个等高度和半径,磁极化强度为JEQ的圆柱永磁铁,如图3(a)所示,其等效的磁极化强度可表示为
(3)
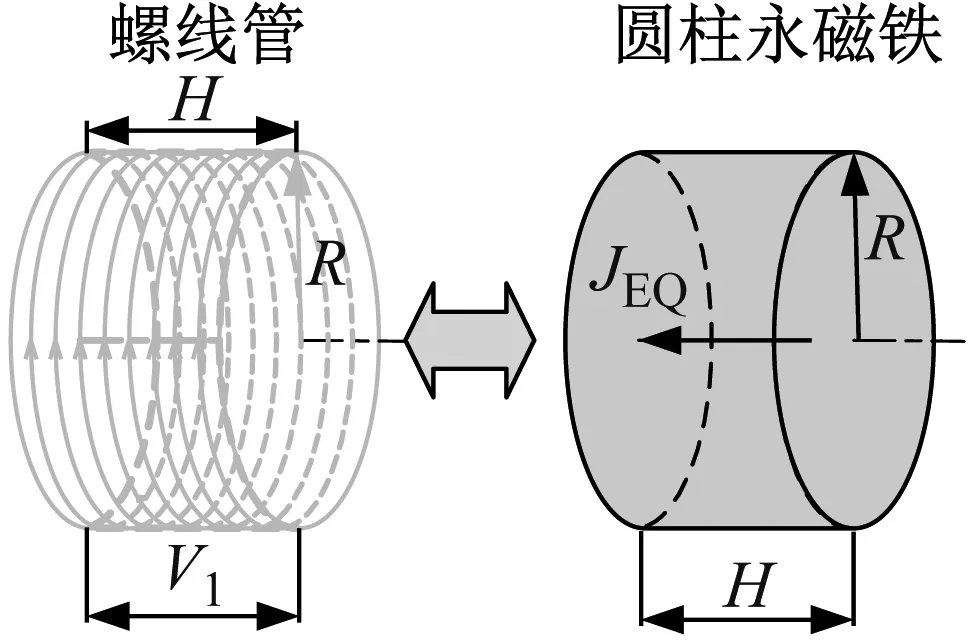
图3 螺线管和环形永磁铁等效
式中,μ0表示真空磁导率。
根据磁场的可叠加性,一个内径为Ra,外径为Rb,磁极化强度为J的环形的永磁铁可以等效为两个外径分别为Ra和Rb的圆柱永磁铁,其磁化强度JOUT和JIN大小相等、方向相反,可表示为
J=JOUT=-JIN
(4)
(2) 线圈和环形永磁铁磁力计算
根据螺线管和环形永磁铁的等效,线圈和环形永磁铁之间的磁力计算,可以等效为多层螺线管叠加与两个圆柱永磁铁的计算,如图4所示。构成线圈的铜导线的直径为d,沿着轴向和径向均匀排列。U表示构成线圈的螺线管沿径向分布的数量;V表示组成螺线管的导线环的数量,螺线管的高度H=V×d,线圈的总圈数可以表示为U×V,螺线管的最小半径为Rc。线圈等效后的磁极化强度JEQ等于等效后的圆柱永磁铁的磁极化强度。对于环形永磁铁等效为两个高度h相同,半径为Ra和Rb的两个圆柱永磁铁。极化强度为JOUT和JIN。单个线圈和环形永磁铁之间的磁力FCpMq,表示为
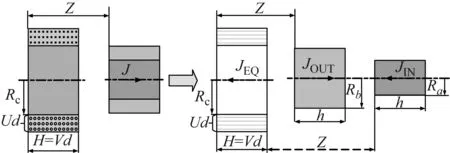
图4 线圈和环形永磁铁等效
(5)
(6)
式中:r(u)表示线圈等效的螺线管半径;Fp(r(u),Ra,Rb,h,Z)表示螺线管等效为圆柱永磁铁后与环形永磁铁等效的两个圆柱永磁铁的磁力,可表示为[20-21]
JOUTf(r,Rb)]
(7)
其中间转变等式f(r,R)为
(8)
其中i表示积聚在螺线管等效圆柱永磁铁圆形端面的磁荷极性,正磁荷为1,负磁荷为-1;同理,j表示积聚在环形永磁铁等效圆柱永磁铁圆形端面的磁荷极性。
其中f′表示为
(9)
K(·)、E(·)和Π(·)分别表示第一类、第二类和第三类完全椭圆积分,其中:
(10)
(11)
(12)
(13)
1.3 电磁负刚度的近似表达
式(5)~(13)组成的表达式代入到式(1)和(2)能够准确的表达磁力和负刚度的大小,然而,由于含有多个完全椭圆积分,形式过于复杂,很难直接应用于动力学建模。所以,对电磁力和负刚度的表达式进行合理的简化以便建立简洁的动力学模型。
假设负刚度kN(I,Z)关于电流I和位移Z的表达式为
kN(I,Z)=k1(I)+k2(I)Z2
(14)
式中,k1(I)和k2(I)Z2是关于电流的函数。在位移Z[-5,5]mm,表1所示的负刚度结构参数代入式(1)~(13)求得的精确值,用最小二乘法拟合负刚度的近似表达式为
kN(I,Z)=-4 962.5I+213.2IZ2
(15)
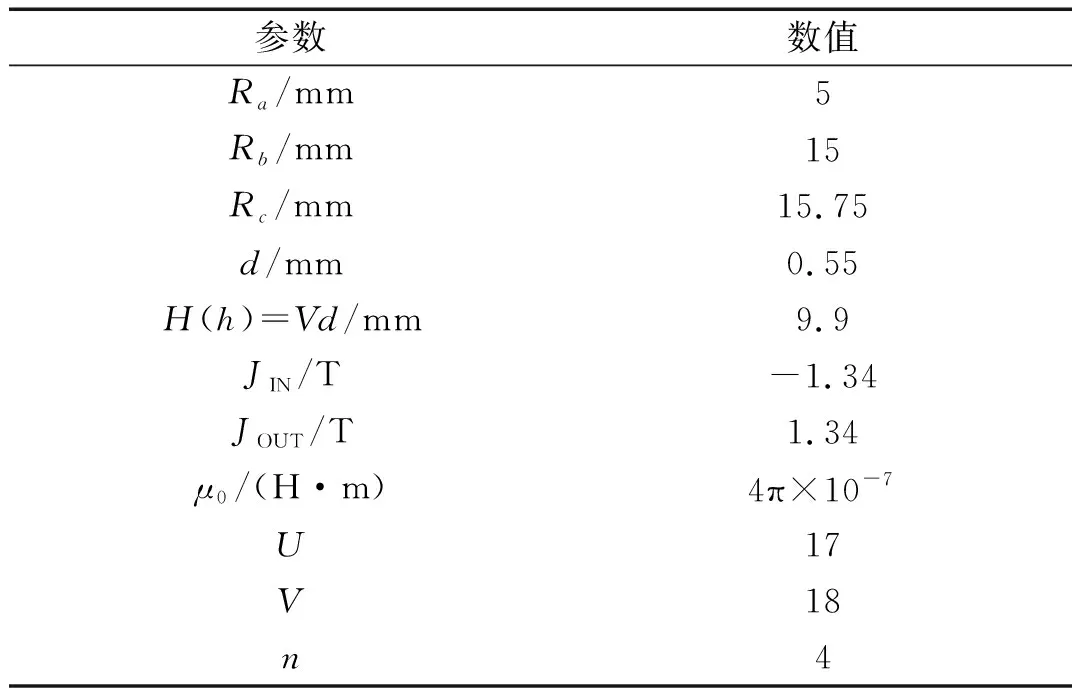
表1 负刚度结构参数
精确解与近似解的对比,如图5所示。可以看出,精确解和近似解具有较好的一致性,负刚度关于位移的变化呈现出非线性特性,最大负刚度位于相对位移为零处。
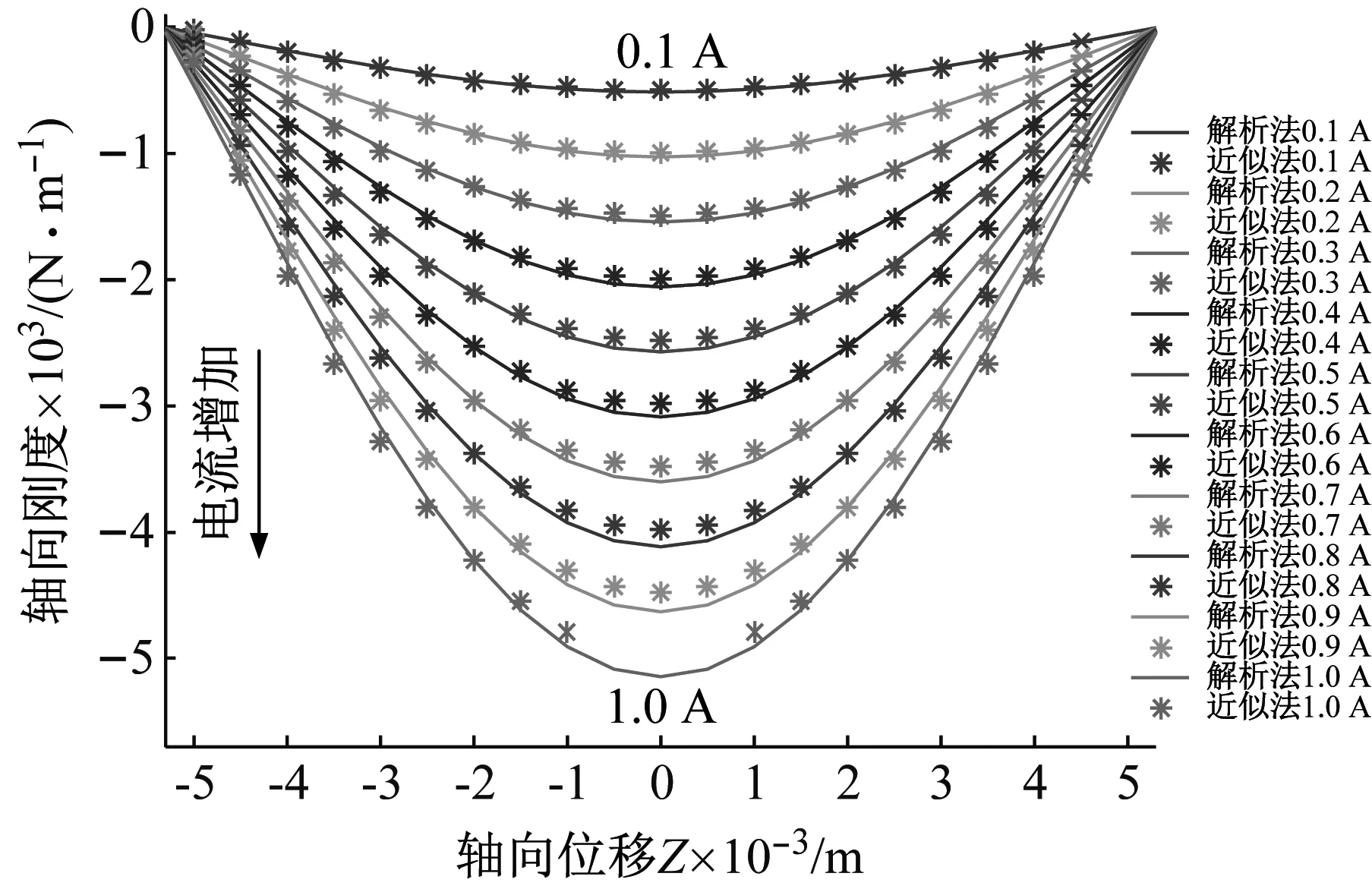
图5 刚度表达式近似法与解析法对比
2 正负刚度并联隔振器
正负刚度并联隔振器隔振方向为水平方向,结构图如图6所示。
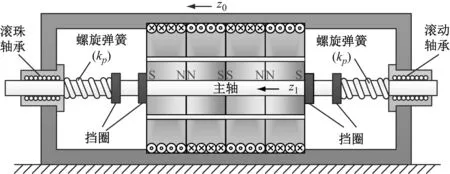
图6 正负刚度并联隔振器结构图
线圈和永磁铁提供负刚度(kN),螺旋弹簧提供正刚度(kP),固定在主轴上的所有质量定义为隔振质量m,z0表示机架的激励位移,z1表示隔振质量位移,隔振质量相对于机架的位移z=z1-z0,根据牛顿第二定律和达朗贝尔原则,系统可表示为
(16)
当支座水平方向上位移为
z0=Z0cosωt
(17)
对式(16)进行无量纲化处理,可表示为
(18)
其中:
(19)
α的符号决定了隔振器的非线性特性的类型,由于[2KP+k1(I)]和k2(I)的符号都为“+”,所以,无量纲化的非线性系统呈现硬特性。这里的ωn表示的不是隔振器的固有频率,而是隔振器在αx3≪1时线性状态下的自然频率。
假设无量纲表达式的位移为
x=Xcos(Ωτ+Φ)
(20)
采用谐波平衡法对无量纲化的表达式(18)进行求解可得
(21)
3 电流对正负刚度并联隔振器的控制特性
式(18)为隔振系统的动力学模型,其中非线性系数α和ζ阻尼率决定了系统性质。而式(19)中关于α和ζ的表达式都是关于电流的变量。电流的变化导致α和ζ的变化,从而改变式(18)表示的隔振系统的性能,实现电流对隔振性能的控制作用。
3.1 电流对阻尼率和非线性系数的作用
根据式(19)中的ζ和ωn的表达式进行整理可得激励电流I对阻尼率的作用表达式,代入表2和近似表达式(15)的参数,ζ可表示为
(22)
励磁电流对阻尼率的作用,如图7所示。随着励磁电流的增加,无量纲表达的系统的阻尼率随电流的增加而增大。观察图形可以发现,电流对阻尼率的作用是非线性的。值得注意的是,随着电流从0增加到1.0 A,阻尼率从0.09增加到了0.16。
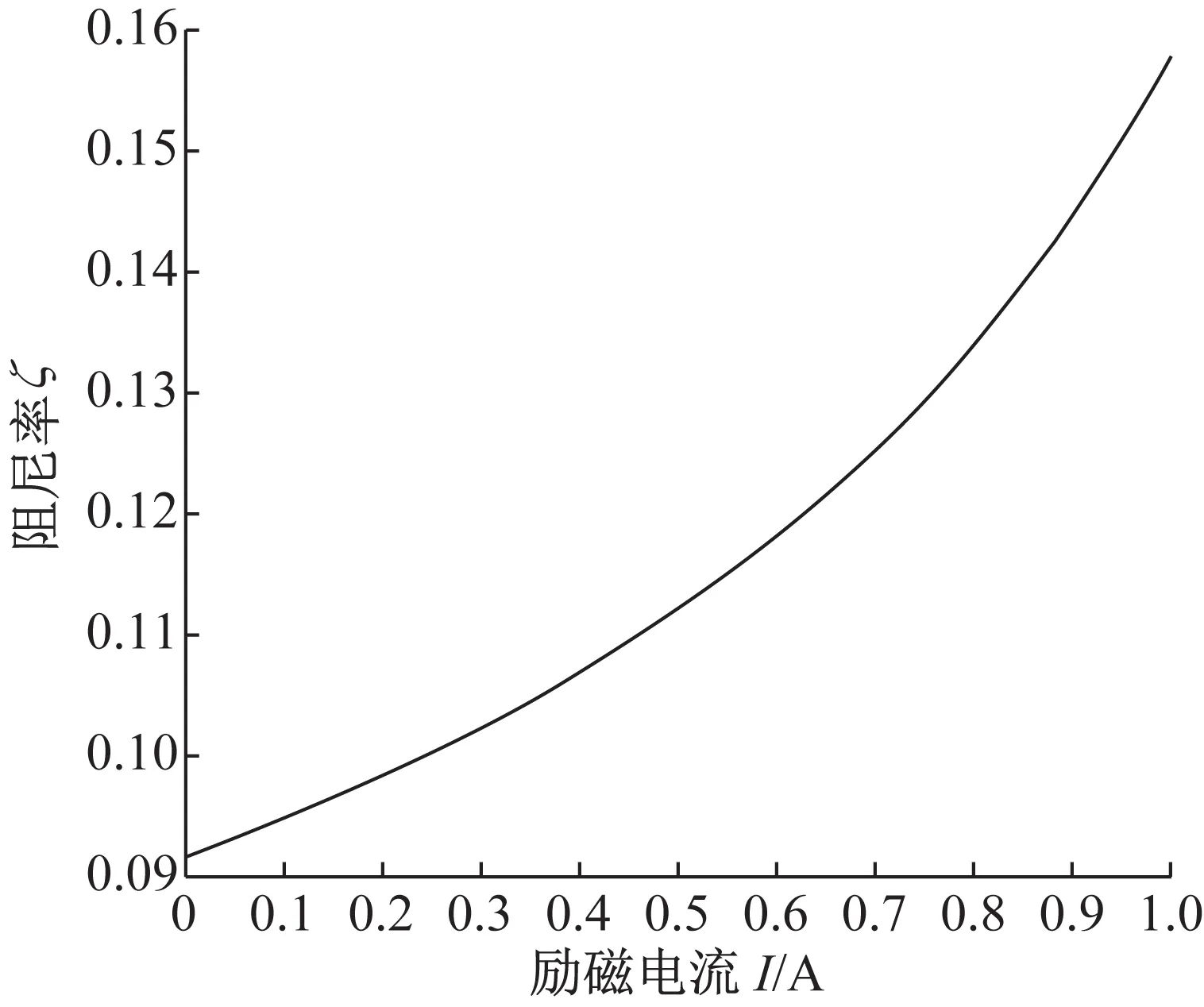
图7 励磁电流I对阻尼率ζ的作用
根据式(19)中非线性系数α的表达式进行整理可得激励电流I对阻尼率的作用表达式,代入表2和近似表达式(15)的参数,α可表示为
(23)
从式(23)可以发现,励磁电流I对非线性系数α的作用受到激励幅值Z0的影响,不同激励幅值下,励磁电流对非线性系数的作用,如图8所示。可以看出,在固定幅值激励下,励磁电流增大,非线性系数也随之增大,并且励磁电流I和非线性系数之间的关系是非线性的。值得注意的是,相比激励幅值Z0对非线性系数的影响明显要比励磁电流I对非线性系数的影响大。
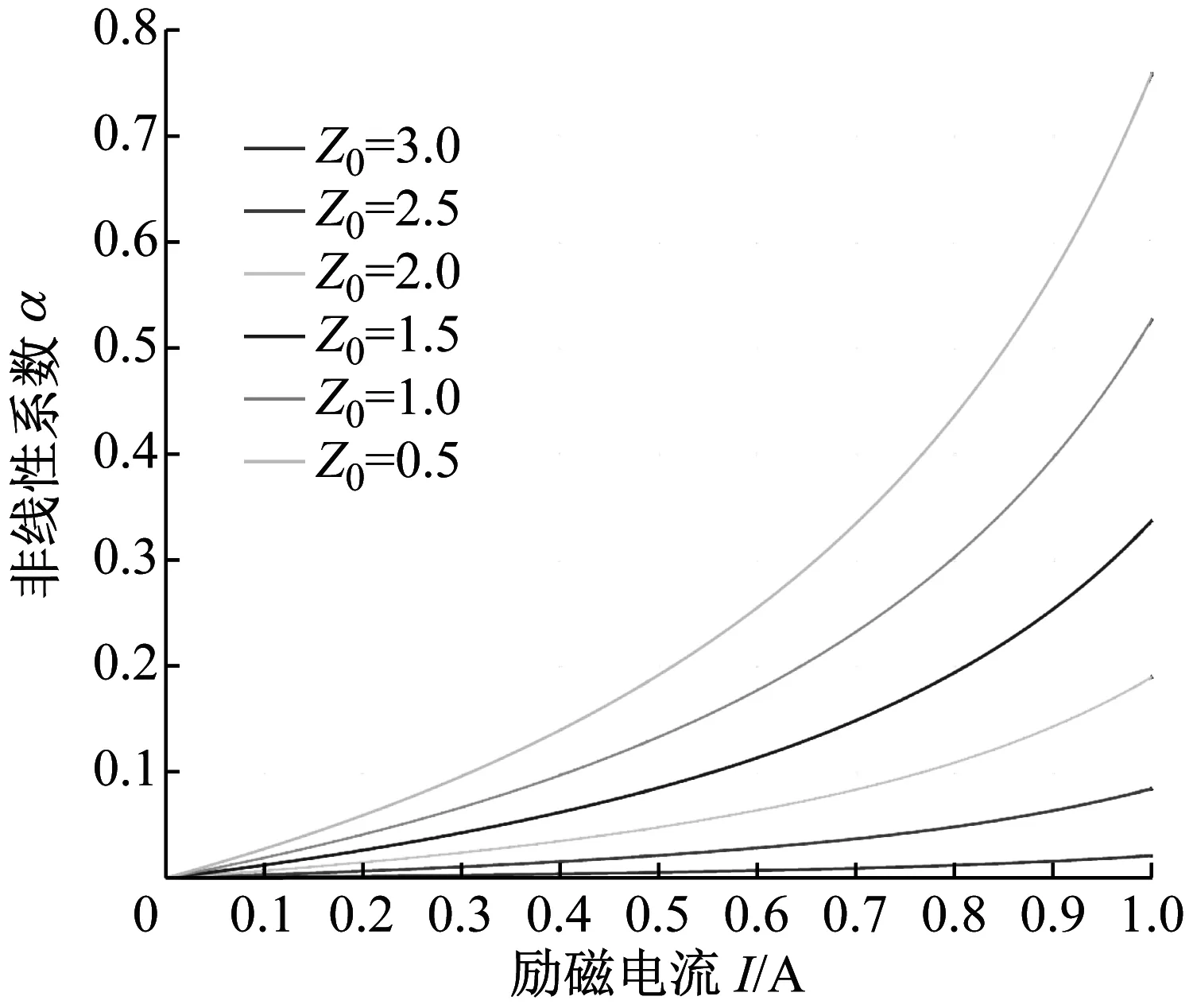
图8 励磁电流I对非线性系数α的作用
3.2 电流对振动传递率的作用
若振源为地基的横向运动,那么绝对位移传递率定义为隔离质量的位移与地基位移幅值的比值,可表示为
(24)
对式(16)采用谐波平衡法求解后代入式(24),绝对位移传递率的表达式为
(25)
由式(25)表示的绝对位移传递率与激励频率在(Z0=0.9 mm)的关系如图9所示。可以看出,绝对位移传递率曲线受到电流的控制作用,电流为零时,呈线性特性,不发生频率跳跃现象。随着电流增大,传递率曲线出现非线性特性,发生频率跳跃现象,电流越大,非线性程度越明显。由于励磁电流具有增大阻尼率的特性,传递率的共振峰值随着电流增大而减小,这对提升系统的隔振效果是有益的。
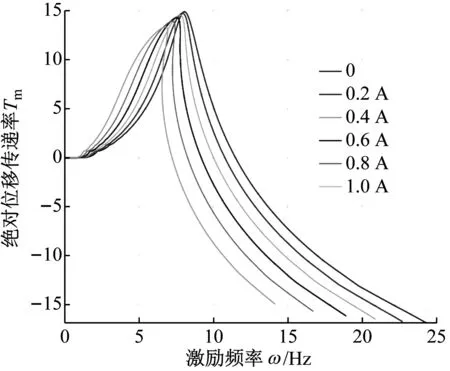
图9 非线性状态下励磁电流对传递率的作用(Z0=0.9 mm)
由式(23)图8可以看出,在位移激励较小的情况下,非线性系数接近零,系统趋近于线性系统。从而,当α≪1时,系统绝对位移传递率可近似为线性系统,可以表示为
(26)
由式(25)和式(26)表示的非线性和线性表达式在小振幅激励下的关系如图10所示。从图中可知,在激励幅值较小的情况下,非线性算法和近似线性算法一致性较好,随着电流的增大峰值频率和峰值传递率逐渐减小,励磁电流对其过程具有线性的控制作用。
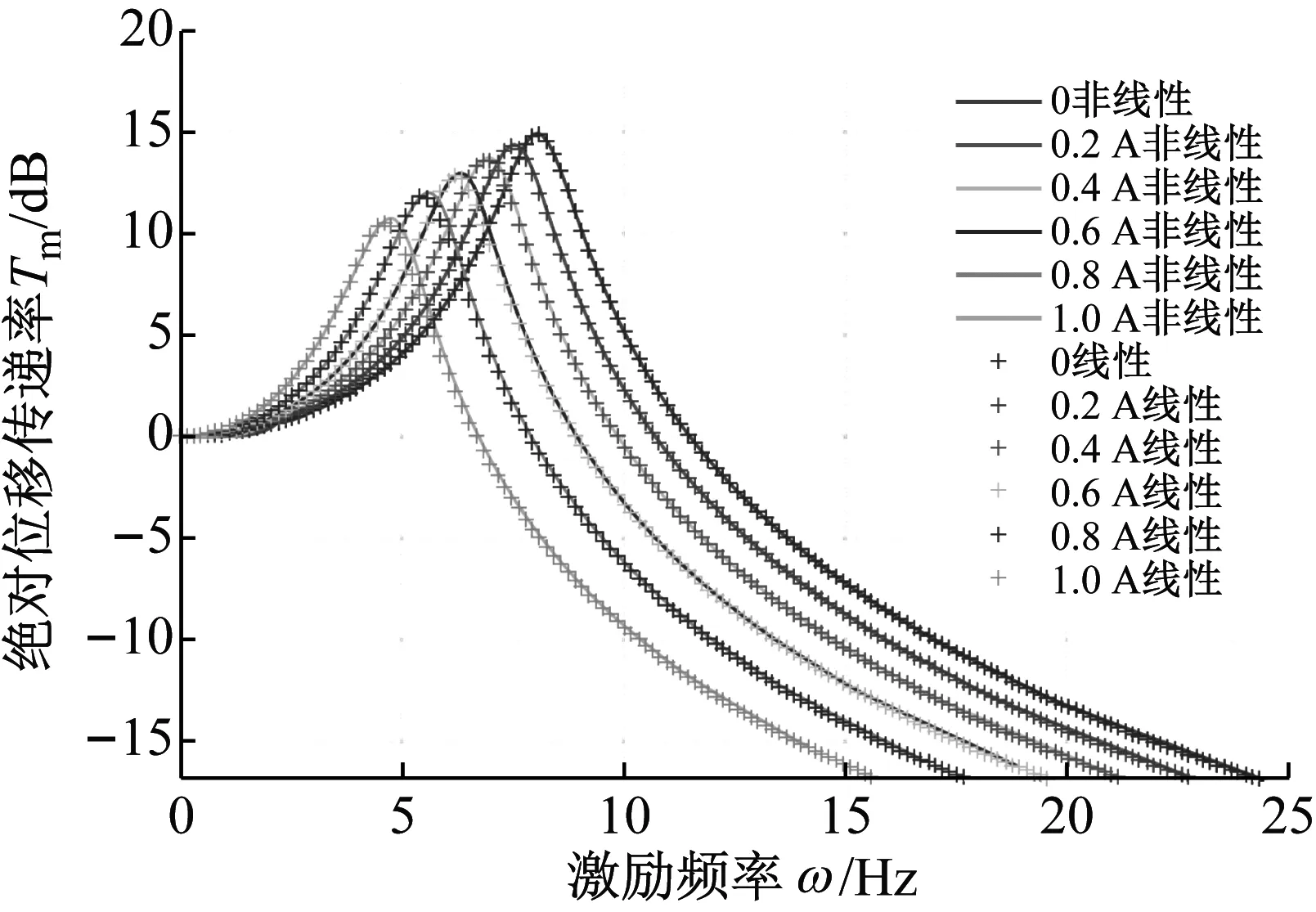
图10 线性与非线性算法传递率比较(Z0=0.3 mm)
4 试验验证
4.1 隔振器试验装置
为了有效的隔绝地面振动对测试系统的干扰,整个测试系统设置在一个气浮隔振平台上。另外,为了减小激励装置与被隔离质量之间振动的耦合,所采用的JZ-2型激振器与测试系统分别位于两个独立的气浮隔振平台上。Gf-20W功率放大器用于驱动JZ-2型激振器,激励信号为10 Hz的正弦信号耦合白噪声。Accelnet Micro Panel ACJ-055-18电流驱动器用于产生线圈内的励磁电流。控制电流的信号和激振器的激励信号由NI控制器(NI PXI-1024Q)产生。另外,被隔振质量的加速度和激励的加速度分别由两个PCB 393B04加速度传感器测量。加速度信号的采集永西门子的LMS SCADAS XS信号采集器采集。所采集数据的处理和传递率的绘制采用LMS Test.Lab软件进行处理。隔振器试验装置如图11所示。隔振器参数通过测量获得,如表2所示。
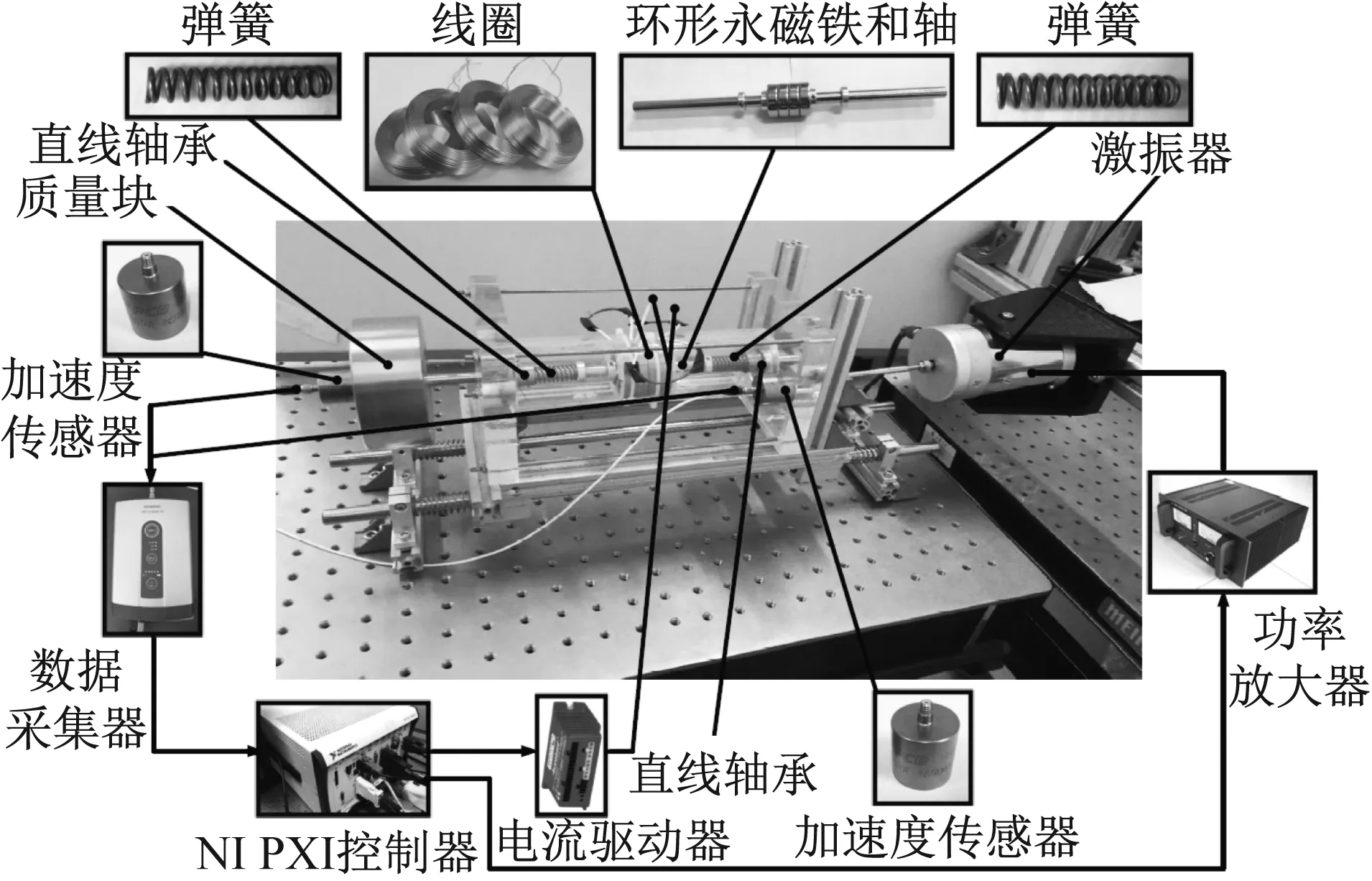
图11 正负刚度并联隔振器试验装置

表2 隔振器系统参数
4.2 试验结果
绝对位移传递率曲线反映隔振器的隔振性能,通过对比不同励磁电流下的传递率曲线可以获得电流对隔振性能的作用。对隔振器线性状态下的传递率进行了测试并与解析算法进行了对比,结果如图12所示。图中的解析解用式(26)进行计算。通过约束激振器的幅值,使得的隔振器工作在线性区间。从图中可以看出,试验传递率曲线与式(26)表达的解析传递率相吻合。励磁电流越大,共振频率越低。随着电流的增大,系统的刚度降低,低频隔振性能提高。由于系统的刚度降低,相同阻尼对系统的共振峰的抑制作用也越大,从图中看一看出共振峰的幅值随着电流的增大在降低。隔振器的低频隔振性能得到提高,而且其提高程度通过励磁电流的大小实现在线控制。
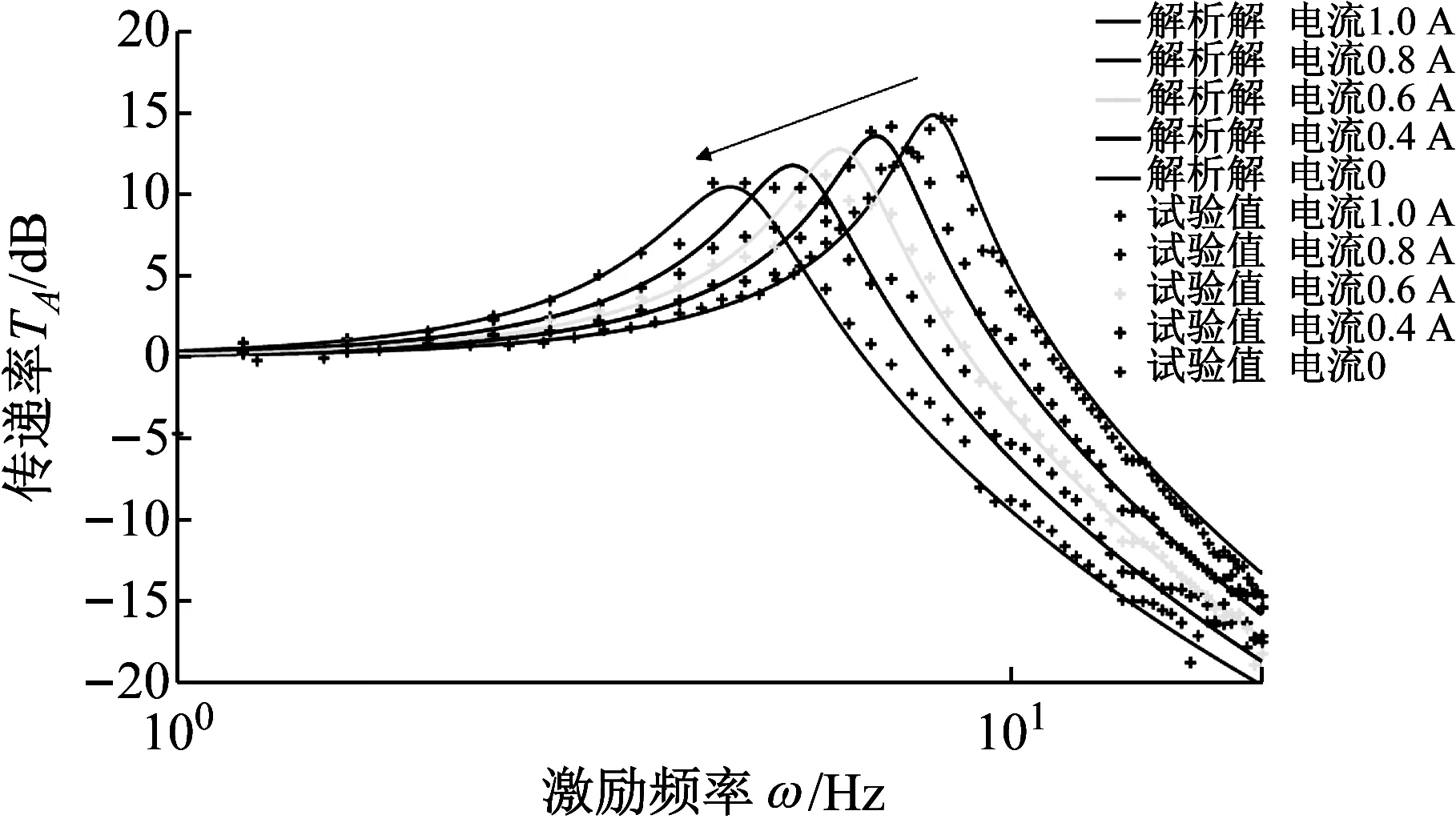
图12 电流对绝对位移传递率控制特性的试验与解析对比
5 结 论
本文提出了一种磁致可控负刚度结构和基于此结构的正负刚度并联半主动隔振器,建立了磁致负刚度和正负刚度并联隔振器的数学模型,并分析了励磁电流对隔振性能的控制特性,为低频隔振技术提供了新的理论方法。主要的结论和研究成果有以下几个方面:
(1) 提出了一种新型非线性磁致负刚度结构,其具有电流可控特性,并推导了磁致负刚度结构的理论模型,分析了电流对负刚度特性的作用原理。由于负刚度理论模型的复杂性不宜直接用于动力学模型,基于近似法建立了电流对负刚度作用模型kN(I,Z)=-4 962.5I+213.2IZ2。
(2) 基于磁致负刚度结构建立了正负刚度并联隔振器动力学,分析了电流对阻尼率、非线性系数的影响和绝对位移传递率的控制作用。电流增大,隔振系统的阻尼率和非线性系数增大,绝对位移传递率共振峰下降,反之亦然。
(3) 建立了正负刚度并联的实验装置,验证了隔振系统动力学模型,实现了线性状态下,当电流变化为0~1.0 A,共振峰的绝对位移传递率由14.9~10.5 dB的变化,低频隔振性能优异。
后续研究:
进一步研究励磁电流对非线性状态下的隔振性能,发现励磁电流对系统在大振幅状态下的频率变化规律,从而开发出隔振频带更宽的隔振器。
