基于部分分层抽样的高墩桥梁随机地震响应分析

2022-05-04陈志强郑史雄丁自豪

振动与冲击 2022年7期

陈志强，郑史雄，丁自豪，张金

(1.西南交通大学土木工程学院，成都 610031；2.成都理工大学环境与土木学院，成都 610059)

由于地震发生过程的复杂性和地震波传播路径的不确定性，地震记录通常都表现出很大程度的随机性。此外，桥梁结构本身也存在显著的不确定性，对于桥梁中广泛采用的混凝土材料，其抗压强度通常具有15%～20%的变异性[1]，即使被认为材料性能较为稳定的钢材，HRB335钢筋强度的变异系数也可达7.43%[2]。如何在桥梁抗震性能分析中同时考虑地震激励和桥梁结构两方面的不确定性一直都是国内外的研究热点。

在早期桥梁抗震性能分析中，往往是单独考虑地震激励和桥梁结构自身的随机性[3]。当只考虑桥梁结构的不确定性时，结构随机地震响应分析通常采用随机有限元法，如随机摄动法[4]、正交多项式展开法[5]、人工神经网络方法[6]、响应面法[7]等。然而，此类方法不仅未能考虑地震激励的随机性，而且只能进行少数几个随机变量输入下的结构随机地震响应分析。当随机变量数量较多时，其不可避免的都会遇到维数灾难的问题。随机振动理论主要处理随机地震激励下确定性结构的随机地震响应[8]。现有的随机振动理论，如虚拟激励法[9]，通常都是基于反应谱或者功率谱密度函数，是完全的频域分析方法，因此其只能解决线弹性结构的随机地震响应分析[10]。然而，在实际工程中，大量的桥梁结构都位于高烈度地震区，在其服役过程中不可避免的会受到破坏性强震的作用，从而使桥梁结构产生严重的非线性行为。虽然也有部分学者建立了结构非线性随机振动分析方法，如FPK方程[11]、等效线性化方法[12]、随机平均法[13]、矩近似法[14]等，但该类方法通常都只适用于简单结构，大规模复杂结构非线性随机地震响应的求解仍然是一个巨大挑战。Li等[15-16]从概率守恒原理的物理机制出发，建立了结构非线性随机振动的概率密度演化理论，实现了随机地震作用下结构非线性随机地震响应的高效求解。然而，当采用概率密度演化理论进行结构随机地震响应分析时需要将地震动功率谱转化为时域的地震动样本，将会引入大量的随机变量。在超高维概率空间中进行代表性样本点的选取是一个巨大的挑战。

综述所述可以看到，不论随机振动理论还是随机有限元理论在分析实际复杂桥梁结构非线性随机地震响应方面都还存在较大难度。基于蒙特卡洛模拟[17]的数值模拟方法独立于随机变量的维度和结构复杂性，是获得桥梁结构随机地震响应的有效途径。但是传统的蒙特卡洛模拟是在整个概率空间内进行随机抽样，效率较低。Shields等[18]建立了基于概率空间分解的部分分层抽样方法，提高了简单随机抽样效率，缩减了抽样方差。本文将基于该思想建立完全非平稳地震作用下桥梁非线性随机地震响应分析的部分分层抽样方法。然后以一座典型的高墩大跨连续刚构桥梁为例，对其进行随机地震响应分析，详细研究桥梁结构不确定性和随机参数相关性对高墩大跨桥梁抗震性能的影响，从而为桥梁的抗震设计和地震可靠度评估提供指导。

1 桥梁结构非线性随机地震响应分析

对于一个非线性随机动力系统，地震作用下，结构动力方程可以表示为

(1)

(2)

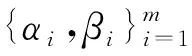
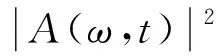
(3)

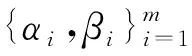
E[αi]=E[βi]=0,E[αiβj]=0

E[αiαj]=E[βiβj]=δij

(4)

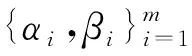
αi=Rand(cas(iΘ1)),βi=Rand(cas(iΘ2))

(5)

其中，Rand(·)为确定性的一一映射算子；cas(·)为Hartley正交基函数，cas(·)=sin(·)+cos(·)。

Z(t)=φ(ζ,Θ,d,t)

(6)

式中：φ(·)为与桥梁结构有关的确定性函数；d为确定性参数向量。

若采用随机抽样方法对式(1)中的非线性随机动力系统进行求解，即可得到桥梁结构地震响应的N个样本。在此基础上，桥梁结构非线性随机地震响应分析所关心的均方值可以表示为

(7)

2 基于部分分层抽样的桥梁随机地震响应估计

(8)

(9)

(10)

ui=R(u1,i,u2,i,…,uS,i)

(11)

式中，R(·)表示随机匹配函数。通过将均匀分布的样本点采用等概率变换即可得到在特定概率分布空间内随机参数的样本点。关于拉丁化部分分层抽样方法的更多细节，也可见文献[18]。

考虑一种概率空间划分的特殊情况，将概率空间RU划分为二维概率空间和一维空间的组合。当RU的维度d为偶数时，可以将其分解为d/2个二维子空间。而当RU的维度d为奇数时，可以分解为(d-1)/2个二维子空间和1个一维子空间。然后，在每一个二维子空间中分别采用随机抽样方法得到均匀分布样本点，再通过所有子空间中样本的随机组合即可得到原始d维概率空间RU中的样本点。

众所周知，随机抽样方法都是随机收敛的。结果的变异性通常由两部分组成：①子空间中随机抽样时的变异性；②将子空间中样本随机匹配到原始d维概率空间中时产生的变异性。如果能够用确定性方法代替随机抽样方法生成低维(二维和一维)子空间中样本点，即可消除低维子空间中生成样本时的不确定性，从而大大减小抽样变异性。基于此，这里将采用Xu等[20]建议的数论方法生成确定性的子空间样本，从而进一步减少拉丁化部分分层抽样中的方差。

对于二维子空间，这里采用Fibonacci序列构造均匀分布的样本点。令F0=F1=1，则Fibonacci序列可以表达为如下递推表达式

Fl=Fl-1+Fl-2,l=2,3,…

(12)

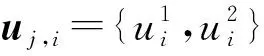
(13)

(14)

式中，int(·)表示截尾取整算子。另外，式(13)和(14)也可等效于

k=1,2;i=1,2,…,N

(15)

式中，整数向量[ζ1,ζ2,N]表示生成算子，对于二维概率空间，N=Fl，ζ1=1，ζ2=Fl-1。

对于一维概率空间，均匀分布的样本点则可以通过置换序列确定如下

(16)

在获得二维和一维概率空间中的样本点之后，只需要将其进行随机组合，即可得到原始单位超立方空间中均匀分布的样本点

ui=R(u1,i,u2,i,…,uS1,i,u1,i,u2,i,…,uS2,i)

(17)

其中，uj,i(j=1,2,…,S1)为二维概率空间中的均匀分布样本点(S1为二维子空间的数量)；uj,i(j=1,2,…,S2)为一维概率空间中的均匀分布样本点(S2为一维子空间的数量)。最后，通过等概率变换即可将单位超立方体空间中的均匀样本转化为目标概率空间中的样本点

(18)

一旦获得随机参数样本，将其代入式(1)中的结构动力学方程并进行求解，即可得到桥梁非线性地震响应的样本集。由于本文方法为等权重抽样，每个样本的概率均为1/N，所有样本的概率之和为1，因此所有样本将构成完备概率集。在获得桥梁结构地震响应样本后，再根据式(7)即可得到桥梁随机地震响应的均方值。基于部分分层抽样的桥梁随机地震响应分析主要步骤如下：

(1) 给定桥梁结构随机参数向量ζ=[ζ1,ζ2,…,ζd1]T和地震动随机参数向量Θ=[Θ1,Θ2]T，定义概率空间RU；

(2) 将概率空间RU分解为(d-1)/2个二维子空间和1个一维子空间或者d/2个二维子空间，在每个二维子空间中通过式(13)和(14)生成均匀分布样本点，并通过式(16)生成一维子空间中的均匀分布样本点；

(3) 依次从每个子空间中无放回的随机抽取N个样本，并在这个过程中，分别将每一个子空间中的样本进行组合(式(17))，从而生成概率空间RU中的均匀样本点ui(i=1,2,…,N)；

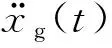
(7) 通过式(7)计算随机地震作用下桥梁结构地震响应的均方值σZ(t)；

(8) 判断桥梁随机地震响应结果是否收敛，若收敛则输出结构的随机地震响应均方值，否则返回步骤2，增大样本数量，直到结果收敛。

基于部分分层抽样的桥梁非线性随机地震响应分析流程如图1所示。

图1 桥梁非线性随机地震响应分析流程

3 高墩大跨桥梁算例分析

3.1 桥梁工程概况及有限元模型

为了说明本文方法在复杂非线性桥梁随机地震响应分析中的应用，以我国贵州省境内的某高墩铁路桥梁作为工程算例进行分析。该桥梁为89 m+168 m+89 m预应力混凝土连续刚构桥，桥梁全长466 m。主梁为单箱单室变截面预应力混凝土箱型梁，主梁材料为C50预应力混凝土，支点截面和跨中截面梁高分别为9 m和12 m，中间按照2次抛物线变化。两个桥墩均为空心矩形变截面，墩高分别为75 m和103 m，这里分别将其编号为1#墩和2#墩，每个桥墩与主梁之间均采用刚性连接。桥墩两端分别支撑与0#桥台和3#桥台，每个桥台均设置盆式橡胶支座约束主梁变形，左侧0#桥台两个支座编号为1#支座和3#支座，右侧桥台两个支座编号为2#支座和4#支座。

桥梁非线性地震响应分析通过OpenSees有限元平台进行[21]。地震作用下主梁的破坏主要以落梁和梁端碰撞为主，主梁本身通常都处于线弹性阶段，因此这里采用弹性梁单元进行模拟。作为高墩桥梁中的关键构件，桥墩在地震作用下可能发生严重的塑性变形，这里采用非线性纤维梁柱单元模拟。根据桥墩的配筋情况，将桥墩截面分为核心区混凝土纤维和保护层混凝土纤维和纵筋纤维三部分，核心区混凝土和保护层混凝土材料特性均采用Concrete02材料进行定义。钢筋材料特性采用Steel02材料进行定义。支座均采用零长度单元进行模拟，通过硬化材料(Hardening materials)定义支座非线性特性[22]。考虑到主梁与桥台之间可能否发生严重的碰撞，这里采用零长度单元结合碰撞材料(Impact Material)模拟梁端碰撞效应，充分考虑碰撞过程中的刚度变化和能量耗散，其本构模型为Hertz-damp模型[23]。桥梁结构有限元模型如图2所示。

图2 桥梁结构有限元模型示意图

3.2 桥梁结构参数不确定性

受到施工误差、材料制造缺陷等因素的影响，桥梁结构的几何尺寸、材料参数、边界条件等通常都具有显著的不确定性。在静力作用下，桥梁结构响应的变异性与结构参数的变异性通常在同一水平，但是在地震作用下，特别是当结构进入非线性后，桥梁结构的随机性将使得其地震响应存在大幅的随机涨落现象。在桥梁结构动力分析中充分考虑桥梁结构参数的不确定性对于桥梁的抗震性能分析具有重要意义。本文参考既往研究[24-25]，以12个对桥梁抗震性能影响较为显著的参数作为结构随机变量，并考虑各个随机参数之间的相关性，进行桥梁的非线性随机地震响应分析，详细研究桥梁结构参数不确定性和相关性对高墩桥梁概率抗震性能的影响。桥梁随机参数的概率分布信息如表1所示，各个参数之间的相关系数如表2所示[24]。

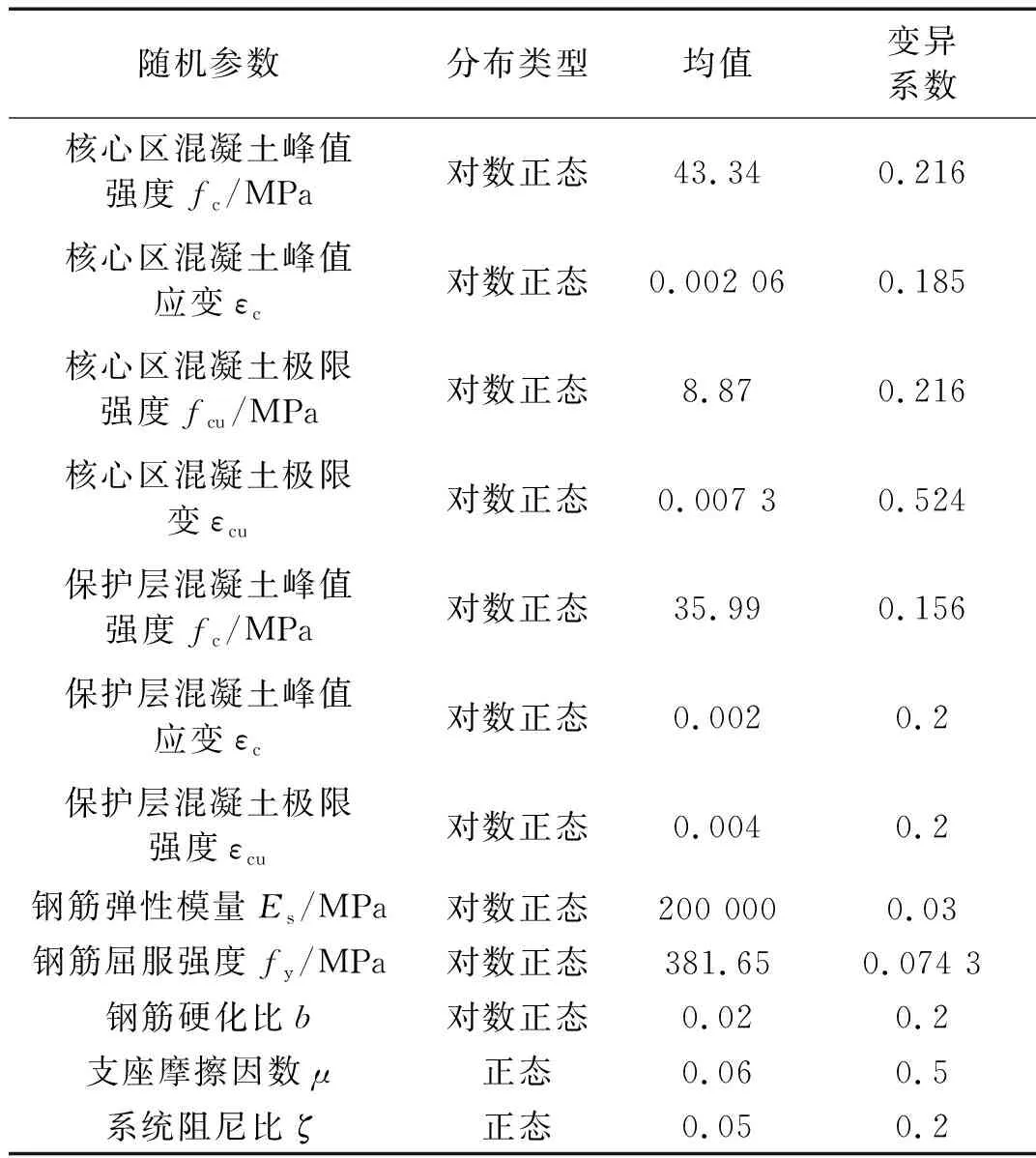
表1 桥梁结构的随机参数概率分布

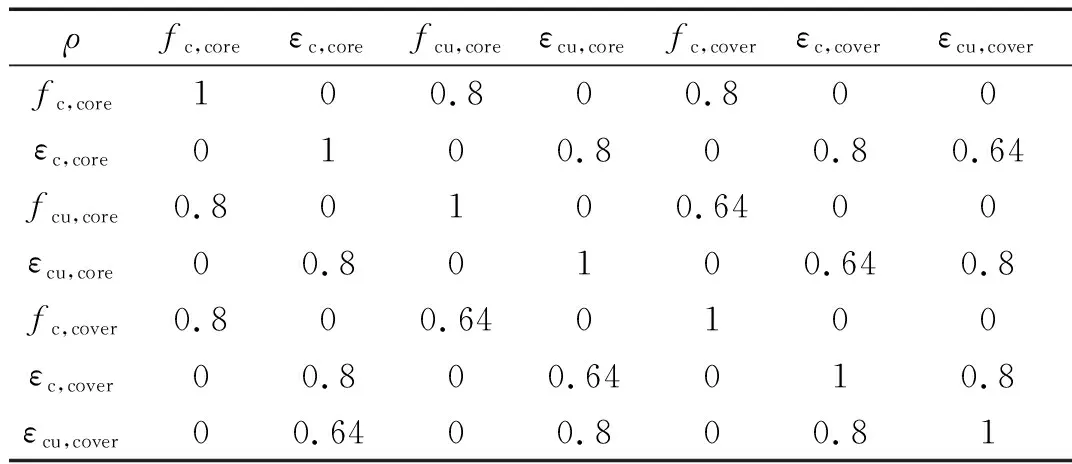
表2 桥梁结构的随机参数相关系数

3.3 随机地震作用模型

桥梁地震响应分析的一个关键问题是输入地震动的确定。由于地震发生的时空不确定性，桥梁位置处的地震动不仅具有显著的随机性，而且地震记录还存在明显的时-频非平稳性。为了考虑地震动的随机性和非平稳性，这里采用文献[26]中的演化功率谱(evolutionary power spectral density, EPSD)模型生成随机地震记录，从而对桥梁结构进行随机地震响应分析。地震动的双边演化功率谱表示为

(19)

式中：A(t)为地震动的非平稳调制函数；S0(t)为谱强度因子。A(t)和S0(t)分别定义为[27]

(20)

(21)

(22)

将抽样获得的地震动随机参数Θ的610个样本Θi(i=1,2,…,610)分别代入式(2)进行地震动模拟，由此即可得到610条地震记录样本。其中两组典型地震记录样本如图3所示，模拟地震动记录样本均值和均方值与目标值的对比如图4所示。从图3中可以看到，模拟的地震动样本不仅幅值存在非平稳，而且其频率也存在显著的非平稳性，这完全符合地震动是时-频非平稳随机过程的认知。从图4中可以看到，模拟地震动均值和均方值与目标值均吻合较好，这说明当样本数N为610时，部分分层抽样方法可以较好地模拟地震动的不确定性。

(a) 样本1

(a) 均值

3.4 桥梁随机地震响应分析

基于之前生成的非平稳地震动样本和采用部分分层抽样获得的桥梁结构随机参数，将桥梁结构随机参数和地震动记录样本分别赋予每一个桥梁结构非线性有限元模型，然后进行一系列的非线性时程分析，即可得到非平稳地震作用下随机桥梁结构的地震响应样本，再通过统计分析即可得到其随机地震响应。图5以其中一个响应样本为例，给出了1#墩墩底截面的弯矩-曲率滞回曲线。从图5中可以看到，在该地震作用下，桥墩产生了明显的屈服，桥梁结构产生了显著的非线性。

图5 桥墩非线性地震响应样本

为了确定该高墩大跨连续刚构桥随机地震响应分析中所需要的样本数量，图6以1号墩的墩顶位移、2号支座的位移，以及1号墩和2号墩的墩底弯矩为例，分别给出了当样本数量N为377、610和987时(对应的Fibonacci序列中的l分别为14，15和16，上述四个关键响应变量随机地震响应均方值的对比。从图6中可以看到，当样本数量N为377时，上述各响应变量的均方值在峰值附近还存在较大波动，但是当样本数量N为610和987时，上述各响应变量就能得到收敛的结果。由此说明，对于本文中的高墩大跨连续刚构桥，在随机地震响应分析时通过610次确定性非线性地震响应分析即可得到满意的结果。

图6 桥梁随机地震响应

为了定量分析不同样本数对桥梁结构非线性随机地震响应分析的影响，同时说明本文方法在精度和效率方面的优势，表3仍然以图6中的四个关键响应变量为例，给出了样本数量N为377、610和987以及直接采用数论方法(18 984样本)[28]确定样本时，上述四个关键响应的平均峰值因子和桥梁结构非线性动力分析所需要的计算时间。其中，桥梁地震响应的平均峰值因子定义为[29]

(23)

式中:σ[Z(t)]表示桥梁随机地震响应的均方差；E[Zext]表示桥梁随机地震响应的平均极值。

从表3中可以看到，桥梁结构不同关键响应的平均峰值因子存在一定差异，其变化通常在1.8～2.2。这表明，在通过桥梁结构非线性随机地震响应标准差确定均值时，采用相同的平均峰值因子是不合理的。当N为377时，所获得的桥梁非线性地震响应平均峰值因子明显要小于N=987时的结果，而当样本数量N为610时获得的响应平均峰值因子与N=987时的结果已经非常接近，并且当样本数量N为610和987时，其结果与直接采用数论方法的结果都较为吻合。再次表明桥梁结构随机地震响应分析时，采用610个样本即可获得较为满意的结果，同时说明本文方法与数论方法具有相同的精度。另外，从表3中不同样本数量下桥梁结构非线性随机动力响应分析时动力分析所需要的计算时间对比可以看到，当样本数量N为377时，桥梁非线性地震响应分析需要189.3 min，约3.15 h，而当N为610和987时，所需要的计算时间分别为4.37 h和6.08 h，若直接采用数论方法进行分析，则一共需要约272 h，与直接采用数论方法相比，本文方法在效率方面具有明显的优势。基于上述分析，在兼顾精度和计算效率的同时，本文将桥梁结构随机地震响应分析所需要的样本数N取为610。

表3 桥梁结构的非线性随机地震响应平均峰值因子

基于桥梁非线性随机地震响应样本，图7(a)以1#墩为例，给出了地震作用下墩顶位移在[3.5,15] s范围内概率密度演化曲面，图7(b)以t=3 s，8 s和13 s三个典型时刻为例，给出了墩顶位移地震响应概率密度曲线的对比。其中，所有的概率密度均采用核密度估计进行确定。从图7中可以看到，随机地震作用下，桥梁结构的非线性地震响应存在显著的非平稳特征，在地震的开始和结束阶段，结构的地震响应概率密度曲面明显较窄，而在地震动峰值附近，结构的地震响应概率密度明显变宽。此外，从图7(a)中还可以看到，随机地震作用下，桥梁结构的地震响应概率密度演化曲面基本都关于0对称，这从图7(b)也可以看到。由此说明了随机地震作用下，结构的非线性地震响应仍然是0均值的非平稳随机过程。

(a) 概率密度演化曲面

为了说明桥梁结构参数不确定性和随机相关性对高墩桥梁概率抗震性能的影响，图8以1#墩地震响应为例，给出了相关不确定性结构、独立不确定性结构、确定性结构三种工况下桥墩地震响应极值分布及对应的累积概率分布。从图8(a)中可以看到，桥梁结构不确定性对其地震响应的影响较为显著。在上述三种工况下，1#墩位移地震响应极值分布的最大值分别为0.137、0.117和0.128，相关不确定性桥梁结构地震响应极值分布的峰值最大，确定性桥梁结构的次之，独立不确定性结构极值分布峰值最小。此外，从图8(a)中还可以看到，不论是相关不确定性桥梁结构、独立不确定性桥梁结构还是确定性桥梁结构，其地震响应极值分布峰值对应的桥墩位移响应极值均为9.5 cm，这表明桥梁结构的不确定性及随机参数相关性虽然会改变桥梁地震响应极值分布的峰值，但是不会改变其发生概率最大的响应。

(a) 极值分布

一旦获得桥梁地震响应极值分布，根据其损伤极限的定义，通过简单的数值积分即可确定桥梁结构的地震可靠度和失效概率。根据文献[30]的定义，该算例桥梁1#墩发生损伤时的桥墩相对位移临界值为19.25 cm。若将其作为桥梁结构损伤极临界值，相关不确定性结构、独立不确定性结构、确定性结构三种工况下1#桥墩的地震可靠度分别为0.969 6、0.985 0和0.996 9。可以看到，当采用确定性结构和独立不确定性结构时所得到的桥梁结构地震可靠度明显要高于相关不确定桥梁结构的地震可靠度。这说明了在桥梁结构地震可靠度分析时不仅需要考虑桥梁结构的不确定性，还需要考虑桥梁结构随机参数的相关性，不考虑桥梁结构的不确定性和随机参数相关性将高估桥梁结构的地震可靠度。